基于有限PMU配置的配电网故障定位

2022-04-14高红均刘俊勇

电力自动化设备 2022年4期

杨睿，高红均，刘俊勇

（四川大学电气工程学院，四川成都 610065）

0 引言

配电网故障定位对电力系统的运行具有重要意义。快速准确地找出故障位置能大幅缩短故障恢复时间，提高电网供电质量和可靠性，提升用户满意度，同时也能降低运营商的运营成本［1-2］。配电网相较输电网结构更为复杂，支路众多，这给配电网的故障定位带来极大的挑战。随着通信技术和广域测量技术的不断发展，同步相量测量单元PMU（Phasor Measurement Unit）的应用愈加广泛［3］。PMU 能获取配电网中高精度、同步的电气相量数据，其幅值和相角误差分别仅为0.5%和0.01°，这为配电网故障的准确定位提供了条件［4］。近年来，国内外学者对基于PMU 的配电网故障定位方法进行了广泛、深入的研究。

配电网故障定位问题主要研究故障区段定位和故障测距2类问题。在基于PMU的配电网故障定位研究中：文献［5］提出了一种动态同步相量测量的双端阻抗测距算法，将故障时刻线路两端测量相量代入正序网络的测距方程求解故障位置；文献［6］在文献［5］的基础上将线路参数与故障距离同时作为优化变量，无需线路精确参数，采用内点法对双端阻抗法进行改进，提高了测距精度；文献［7］基于数据统计理论，提取同步数据的故障特征，利用同步数据统计特性判定配电网故障区域和故障时刻。上述方法对PMU 安装数量要求较高，需全网配置。由于PMU设备造价高昂，且大量的PMU 会导致数据量过于庞大，对系统通信要求较高，不宜在配电网中广泛使用［8］。因此，考虑如何使用有限的PMU 实现故障定位具有重要意义。文献［9-14］提出了在有限PMU情况下的故障定位方法。文献［9］根据电压信号时频特性以及电网拓扑结构生成故障定位图、确定故障点。文献［10］研究了在实时网络拓扑结构和负荷变化情形下的故障区段定位方法，但该方法只能定位到装有PMU 设备的两测点之间，定位范围较大。文献［11］提出利用有限PMU 测点同步相量，根据故障线路两端的系统阻抗等值模型和故障点注入电流等值模型实现故障测距。文献［12］通过优化PMU配置，利用少量的PMU 快速确定故障域，通过虚拟电流和实测电流比值实现故障测距。文献［13］利用少量PMU，将线路分为3类故障检测域，并提出了可疑故障元件集的搜索判据，然后利用各节点的全局向量信息实现配电网区段定位。文献［14］考虑了含有特殊负荷的配电网，并提出了一种分层分布式故障定位方法，该方法能有效避免负荷扰动对故障定位的影响。上述研究中，多数方法仍需系统节点半数以上的PMU，才能准确定位故障，且关于多重故障的研究不多。基于此，文献［15-17］提出了利用压缩感知理论，通过重构故障电流中非零元素的位置确定故障位置。压缩感知是近年来信号领域中新建立的理论，其最大的特点就是可以通过少量的采样信号，在原信号为稀疏信号的情况下（自然界中几乎所有信号都可以转换或近似转换成稀疏信号）准确地还原出原信号。文献［15］根据稀疏向量的结构约束，提出了基于贪婪思想的求解算法，避免了出现伪故障点的问题，但贪婪类算法易误判故障区间，导致故障定位失败。文献［16-17］采用的贝叶斯重构算法在单故障情形下求解精度较高，但对多重故障的定位效果一般。

针对配电网故障定位的研究现状，本文提出一种基于有限PMU 的配电网故障定位方法，该方法在单故障和多重故障2 种场景下都能实现故障测距：通过叠加原理和等效变换推导故障分量网络中故障点注入电流源的等效模型，对复数形式的节点电压方程解耦，得到实数形式的压缩感知模型，利用ℓ1正则化最小二乘法重构近似故障电流向量；设定阈值选取归一化重构电流向量中的主导元素，确定可疑故障区间；根据电压残差和故障测距结果确定真实故障区间和最终故障点位置。

1 故障等效模型

图1 为故障网络及其分解示意图。由叠加原理可知图1（a）能分解成正常运行和故障分量网络，如图1（b）所示。图中：Z1、Z2为电源等值阻抗；U1、U2为电源电压；G1、G2为电源端电压节点；D1、D2为负荷节点；ZD1、ZD2为负荷阻抗，负荷采用恒定阻抗模型；f为故障点；Vf为故障点处的节点电压。

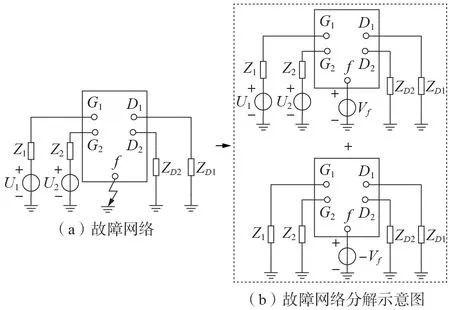
图1 故障网络及其分解示意图Fig.1 Schematic diagram of fault network and its breakdown diagram

故障分量网络中仅有点f有注入电流-ΔIf。因此对于三相系统而言，故障分量网络节点电压方程如下：

对于所有不同类型的故障，其都包含正序分量，可用对称分量法将式（1）简化为单相系统，如式（2）所示。

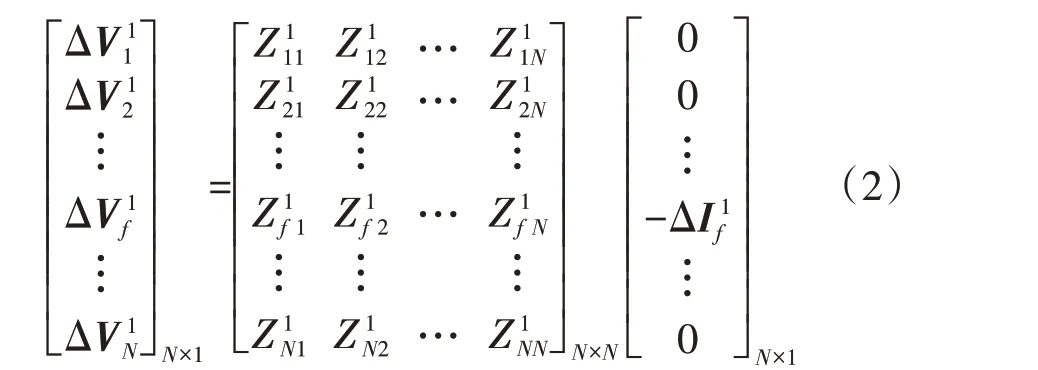
式中：ΔV1i为节点i的正序电压；Z1ii为节点i的正序自阻抗；Z1ij为节点i和j的正序互阻抗；ΔI1f为故障点f的正序故障电流。

考虑更为一般的情况，若故障发生在系统节点之间，故障支路示意图见附录A 图A1。易知通过将故障点作为系统新增节点，可列写故障情况下的节点电压方程，但需要根据故障点的位置重新计算节点阻抗矩阵，所以该方法难以生成新的阻抗矩阵。因此可以考虑将故障点的电流等效至相邻节点上。

由图A1，根据基尔霍夫定律有：

可以看到ij主要由节点j的对地电流、阻抗zjq上流过的电流以及节点注入电流-(1-r)if三部分构成。同理，可以推导出iq的表达式为：

本文选取M个测量点，即从电压向量中选取M（M≪N）个元素以及阻抗矩阵中对应的M行，形成新的欠定节点电压方程：

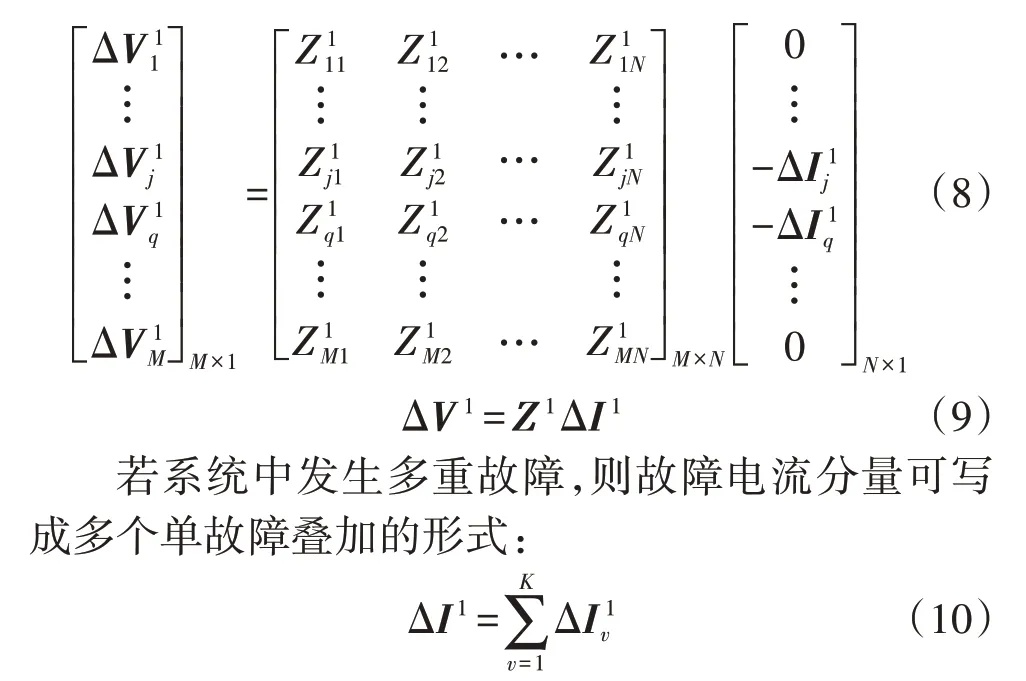
式中：K为故障数量；ΔI1v为第v个故障的虚拟注入电流。因此求解式（9）得到ΔI1后即可知道电流向量中全部非零元素的位置，即故障点所在区段，从而实现故障区段定位。

式（9）为欠定方程，一般而言不存在唯一解。但压缩感知理论指出，当解向量足够稀疏时，存在唯一的稀疏解。

则求解复数方程式（9）的问题被转化为求解实数方程式（13）的问题，便于由压缩感知重构算法求解。

为便于后续分析说明，本文假设当系统中发生多重故障时，每2 处故障均不在相邻线路且故障点都不在节点处。当存在两故障相邻或故障在节点处的情况时，分析过程与本文所述方法类似。

从以上分析可以发现，本文所提方法依赖于故障网络的节点电压方程以及故障点注入电流值，只要当前系统对应的节点电压方程成立，且有较明显的故障电流值，便能有效进行故障定位。换言之，该方法同时适用于交流配电网和直流配电网，若系统正常运行时的拓扑结构发生变化，则需要重新生成对应的节点阻抗矩阵，得到新的故障节点电压方程。对于中性点非有效接地单相接地故障，短路电流过小，故障特征不明显，该方法不再适用。因此本文研究主要针对中高压配电网，其包含的故障类型有小电流接地系统的相间短路故障、相间短路接地故障、三相短路故障以及大电流接地系统所有类型的故障。

2 故障区段定位

2.1 压缩感知框架

自然界的所有信号都可以在某组基向量下展开，转换为稀疏系数。在本文中，故障电流信号本身就是高度稀疏的，因此不必考虑稀疏展开问题。

假设一向量X是S（即非零元素个数）稀疏的，本文采用一个观测矩阵Φ∈RM×N(S＜M≪N)对X进行观测，得到观测向量Y∈RM，这也是高维向量到低维向量的投影过程，如式（14）所示。

参数λ＞0，具有平衡解向量X稀疏度和近似误差（即噪声）的作用。通过ℓ1正则化最小二乘法能求解稀疏向量的近似解。

2.2 确定主导元素

通过上述算法求解得到稀疏向量，用Ir表示。在已有文献中，通常是取绝对值最大的几个元素值作为故障定位结果，但实际上，Ir为近似故障电流，其中的非零元素与实际故障节点并非严格一一对应，会出现误判故障区段的问题。为精确定位故障区段，首先需对重构电流向量进行归一化处理。

Ir是长度为2N的列向量，前N项表示各节点虚拟注入电流的实部，后N项表示各节点虚拟注入电流的虚部，选取重构电流实部的最大元素作为前N项归一化系数，重构电流虚部的最大元素作为后N项的归一化系数，分别如式（19）、（20）所示。

将归一化重构电流向量中大于某一阈值的元素作为故障区间判别的主导元素，将其对应的节点作为可能的故障节点，用于后续确定疑似故障区间集合。

2.3 故障区段定位

其余故障点的电流与最大故障点电流存在相位差，因此不满足上述关系，有可能出现其实部或虚部的值过小，甚至小于规定阈值的情况。在经过大量仿真实验后发现，当设定阈值为0.05时，绝大部分情况下这些故障点至少有1 个实部值或虚部值大于0.05，能够准确地定位故障区间。

综上所述，只要在归一化重构电流向量中，虚部或实部有1 个元素大于设定阈值，那么就应将该主导元素对应的节点作为故障区间的节点之一，假如某一节点在归一化重构电流向量中仅有实部大于阈值，其虚部小于阈值，在计算电压残差时，也应同时选取节点阻抗矩阵中与其实部和虚部分别对应的2列，即在Zreal中对应重构电流实部和虚部的原子总是成对出现的，并且由前文推导可知，与该节点的相邻的某一节点在Zreal中对应的2列也应同时被选取。

在有些情况下，主导元素的位置可能位于实际故障相邻区间的节点上，也可能出现在与实际故障区间相隔一个区间的节点上，为尽可能准确地估计故障区间，本文将以主导元素表示的节点为首节点和末节点的所有支路称为该节点的1 阶故障区间，将与1 阶故障相邻的所有支路称为该节点的2 阶故障区间，依此类推，可得n阶区间故障，其示意图见附录A图A3。

将1 阶故障区间作为初始的疑似故障支路，计算每条疑似故障支路或疑似支路组合对应的电压残差，从中选取电压残差最小的情况作为故障区段定位结果。电压残差计算公式如式（26）所示。

3 故障测距算法

3.1 多重故障测距

通过式（30）求解出ri，便得出第i个故障到该区段节点ji的线路长度占该区段总长度的百分比，实现故障测距。

显然，ri应满足0≤ri≤1。若存在某故障支路组合，使得所有的ri均满足约束，则将此结果作为最终定位结果。若不存在这样的故障支路组合，使得所有ri满足该约束，则应扩大疑似故障区间，将n+1 阶故障区间也纳入疑似故障区间，形成新的疑似故障支路组合代入式（26）重新计算电压残差和故障距离，直到ri满足条件为止。该测距方法适用于任意故障个数的故障测距。

一般地，实际中发生单个故障的概率较大，下面提出一种对于单个故障的测距方法，能避免复数矩阵的运算，极大地降低了运算量。

3.2 单故障测距

文献［17］证明了节点阻抗矩阵有较强的列相关性，按照文献中的描述：对于系统中某一区域j-q，若节点j更靠近参考节点，则更靠近节点j的节点（包含节点j）称为上游节点i，更靠近节点q的节点（包含节点q）称为下游节点m。阻抗矩阵各元素的关系为：

与多重故障情形类似，若无r满足约束条件，则应扩大疑似故障区间，重新计算新区间下的电压残差和r，直到r满足约束。

从式（34）可以看出，仅需要故障区段上游和下游各1 个测点电压的值以及节点阻抗矩阵中的元素便可实现故障测距，测点电压和阻抗矩阵都是已知的，采用该方法求解简单，无需计算节点注入电流。

3.3 故障定位流程

在已知故障数目的情况下，通过前文所述方法能求出故障的具体位置，但在实际中无法预先得知系统中发生的故障数目，这会对故障区段定位和故障测距造成困难。由于故障重构电流向量并非精确解，其中的非零元素并不能与实际故障点一一对应，所以也不能简单地通过非零元素的个数确定实际故障个数，这也是压缩感知在故障定位中应用的局限性，在利用此类方法的研究中尚无关于故障个数的判别方法，大多都是在已知故障个数的情况下进行故障定位的。为避免计算故障个数的问题，采用循环遍历的方式，通过电压残差公式和故障测距公式依次计算可能故障数目下对应的电压残差，直到电压残差最小，且ri满足0 ≤ri≤1的条件，将该支路或支路组合作为故障测距最终结果。通过此方法即使在不知道故障个数的前提下，也能有效进行故障定位。

本文所提故障定位算法流程如图2所示。

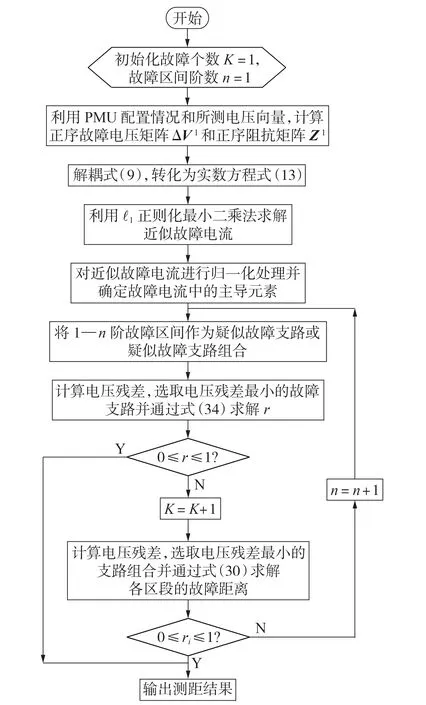
图2 故障定位算法流程图Fig.2 Flowchart of fault locating algorithm

4 算例分析

在Simulink中搭建IEEE 33节点测试系统，仿真采样频率为4 kHz，使用MATLAB进行数据分析和计算，验证本文所提故障定位算法的有效性。

实现故障定位必须满足的条件是在故障的上游和下游至少各存在1 个测点，因此为实现全网故障定位，电源出口和各支路末端必须布置量测装置，同时，为提高定位精度，还应在支路阻抗较小的节点附近增设量测装置［16］。分别在节点1、8、11、17、21、24和32 处放置7 台PMU，通过大量仿真实验发现，在此配置下，对于线路中单故障定位的求解能有较高的精度，但在多重故障定位中，则需要增加一定的测点数量，才能成功定位多重故障位置。根据仿真模拟的结果，除了原本配置的7个测点外，在节点3、19、25、30 处增设4 台PMU 装置，能取得较好的定位结果，如图3所示。

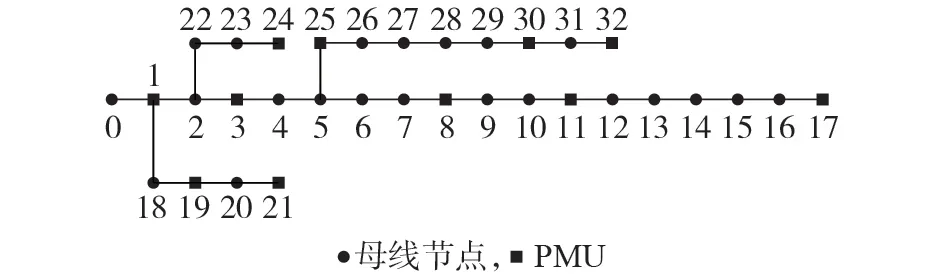
图3 IEEE 33节点系统的PMU配置图Fig.3 PMU configuration diagram of IEEE 33-bus system

定义故障距离的计算值和实际值的相对误差δ为：

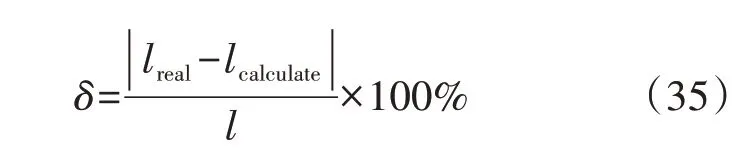
式中：lreal和lcalculate分别为故障点到相邻最近的某一节点的距离的实际值和计算值；l为该故障点的相邻两节点之间的线路长度。

4.1 单重故障定位仿真分析

在节点25和节点26之间设置BC两相接地短路故障，过渡电阻为0，故障点位于距离节点25占支路长度的30%处，记为“25，26BCG-0 Ω（30%）”。此时系统中测点处的故障电压正序分量见附录B表B1。

通过ℓ1正则化最小二乘法求解式（18），得到重构电流，然后按照式（19）和式（20）对重构电流进行归一化处理，结果如图4所示。

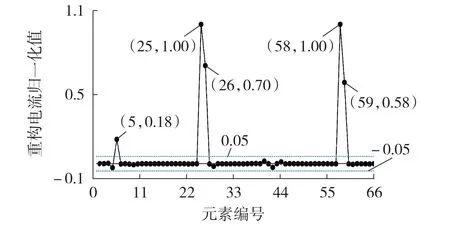
图4 单故障重构电流归一化值Fig.4 Normalized value of single fault reconstruction current

按照2.3 节所述，将节点5、25、26 对应的元素作为主导元素，将这些节点的1 阶故障区间作为疑似故障支路。将全部疑似故障支路代入式（26）和式（34）分别计算电压残差和故障距离，选取电压残差最小且r满足0≤r≤1 的条件的支路作为故障区段定位结果，具体计算结果见附录B表B2。r表示故障点到首节点的距离占故障支路长度的百分比，在理想情况下，计算结果应为实数，但在计算过程中存在计算误差且实际中存在各种干扰因素（如噪声），因此，按此方法计算所得r通常为复数形式，为使得计算结果同r的物理意义保持一致，本文取r的实部作为故障定位结果，本文分析结果都直接给出r的实数值。同时，故障距离不应为负值，因此表中不再给出求解故障距离为负值的结果。从表中可以看出，由节点25、26 计算所得的电压残差远小于其余疑似故障支路节点对应的电压残差，且r满足0≤r≤1 的条件，因此将节点25和26所确定的支路作为最终故障区段定位结果。对比计算结果可以发现，仅有节点5、6 和节点25、26 确定的r满足约束，其余故障支路的计算故障距离均不满足。因此也可以直接计算所有疑似故障区段下对应的r，选取r满足上述条件的区段，再计算电压的残差，最终确定故障点位置。

综上，本次故障定位的结果为节点25和26之间区域，故障点位于距节点25 占支路全长的30.26%处。这一结果与本文设置的故障点位置极为接近，相对误差仅为0.26%，基本满足故障测距要求。

为验证本文方法的有效性与准确性，选择30 个故障点，各故障点分别设置4 类常见故障类型：单相接地短路故障（1-ph-g）、两相短路故障（2-ph）、两相接地短路故障（2-ph-g）、三相接地短路故障（3-ph-g），并设置不同的过渡电阻，求取平均测距误差，计算结果见附录B表B3。

考虑噪声对故障定位的影响，给测点电压实部和虚部分别添加1%的高斯白噪声，计算结果见附录B表B4。

通过对比计算结果可以看出，噪声和过渡电阻会对故障测距结果造成一定的影响，随着过渡电阻不断增大，故障测距的误差也逐渐增大，这是因为过渡电阻越大，故障电流会越小，从而影响测距结果。因此，本文所提方法能耐受一定范围内的过渡电阻，具体范围需根据实际测距误差需求确定。

4.2 多重故障定位仿真分析

本文以双重故障为例进行说明，更多故障情形的故障定位与双重故障的情形类似，本文不再赘述。

考虑含噪声的情形，给测点电压的实部和虚部分别添加1%的白噪声，2处故障的设置情况如下。

1）故障1：节点19 和节点20 之间设置BC 两相接地短路故障，过渡电阻为20 Ω，故障点位于距离节点19 占支路长度的20%处，记为“19，20BC-20 Ω（20%）”。

2）故障2：节点29 和节点30 之间设置A 相接地短路故障，过渡电阻为20 Ω，故障点位于距离节点29占支路长度的50%处，记为“29，30AG-20 Ω（50%）”。此时系统中各测点处的正序故障电压见附录B表B5。

和前文类似，通过ℓ1正则化最小二乘法求解式（18），得到重构电流归一化值，结果如图5所示。

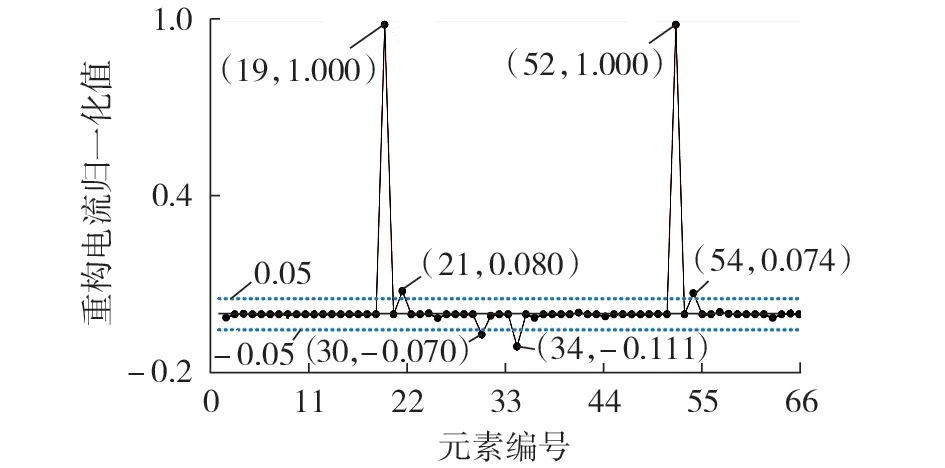
图5 双重故障重构电流归一化值Fig.5 Normalized value of double fault reconstruction current

元素归一化值大于阈值的编号对应节点分别为节点19、21、30，将各节点1 阶故障区间（18，19）、（19，20）、（20，21）、（21，22）、（29，30）、（30，31）作为疑似故障支路，按照图2 所示流程计算，可以发现第1 次迭代（故障个数为1 的情况）所得r均不满足约束，因此进入第2 次迭代（故障个数为2 的情况），将这6 条支路两两组合，形成所有可能的故障支路组合，代入式（26）求解，并通过式（30）计算故障距离，具体计算结果见附录B表B6。

选取电压残差最小一组情况作为故障定位结果。通过计算结果发现支路组合（19，20）-（29，30）以及（20，21）-（29，30）的电压残差基本一致，但后者对应的故障距离r不满足约束条件，前者所求的2处故障距离均满足约束条件，因此选取第1 种支路组合为最终故障定位结果。

综上，本次故障定位结果为故障1位于节点19、20之间距离节点19占支路全长20.57%处，故障2位于节点29、30 之间距离节点29 占支路全长54.04%处，2处故障的相对误差分别为0.57%和4.04%。

通过此算例可以看出本文所提故障定位方法的优势，若按照一般方法分析故障，则首先面临的难题便是难以有效确定故障数量。其次，假设已知故障个数为2，按照图5，若直接取元素绝对值最大的2个节点作为故障节点，此时得到的故障节点是节点1和19，明显与真实故障节点不一致，说明本文所提方法能避免故障个数未知的难题，并有效提高故障定位的可靠性。

本文分别在有噪声和无噪声情形下随机设置200 组的双重故障，噪声为1%的高斯白噪声，故障范围在某一支路距其中一节点占支路长度的1%～99%之间，过渡电阻设为0、20、50 Ω，故障定位结果见附录B表B7。

通过对比可以发现，双重故障定位效果没有单故障定位效果好，单故障情况下，大部分故障定位的误差都在1%以下，而双重故障定位误差大部分都在1%～5%之间，甚至在噪声影响下，还有少量高于10%的误差，但考虑在配电网中，实际线路距离较短，即使是10%的误差，实际需要排查的线路距离仍在可接受范围内，能有效缩小巡检范围。