基于混杂自动机的双向ICPT系统建模及控制

李 欣，徐积强

（1. 兰州交通大学 新能源与动力工程学院，甘肃 兰州 730070；2. 兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070）

0 引言

感应耦合电能传输ICPT（Inductively Coupled Power Transfer）技术因其安全、可靠、灵活等优点被广泛应用于消费电子设备［1］、轨道交通［2］、电动汽车［3］等领域。随着ICPT 技术的发展，ICPT 系统的功率传输方向不再局限于传统的“源”→“荷”，对“荷”→“源”的功率传输也提出了要求。在轨道交通非接触供电系统再生制动能量回收利用和电动汽车无线充电领域，双向ICPT 技术显得尤为重要。其中电动汽车入网不仅有利于电网“削峰填谷”，改善电能质量，还有利于能量的灵活流动，促进能源高效利用。

双向ICPT 系统一次侧与二次侧的能量交互是通过松耦合的互感线圈实现的，存在较大的漏感，因此必须设计相应的补偿网络以减小系统无功［4］。SS型补偿拓扑结构简单且谐振频率与耦合系数和负载无关，但是输出功率随着耦合系数的减小而增大。相比于SS 型补偿拓扑，双LCL 型补偿拓扑感应线圈恒流的特点更适用于多负载无线电能传输系统［5］，但是其外加电感值大，增加了系统体积和成本。对双LCL 型补偿拓扑中的耦合线圈串联补偿电容，将双LCL 型补偿拓扑演变为双LCC 型补偿拓扑。双LCC 型补偿拓扑不仅保留了双LCL 型补偿拓扑的优点，同时解决了双LCL 型补偿拓扑传输功率低和直流磁化的问题［6］。双LCC 型补偿拓扑一、二次侧结构对称，参数设计灵活，同时不受负载阻抗影响，可实现系统恒流源输出［7］，有利于双向ICPT 系统实现能量的双向传输。

ICPT 系统模型可分为稳态模型和动态模型。前者基于互感理论［8］和耦合模理论［9］对系统参数设计及功率传输特性分析，模型简单、直观且利于分析。动态模型建模方法主要利用状态空间平均法［10］、广义状态空间平均法［11］、扩展函数描述法［12］等将不连续、时变模型转化为线性、时不变模型，再对其进行线性化处理，动态模型的建立有利于系统暂态分析及控制。目前双向ICPT 系统建模沿用单向ICPT 系统的建模方法。双向ICPT 系统的工作模态随着开关器件状态的变化而改变，将系统的连续状态量的约束看作连续的子系统，系统的不同工作模式和模态看作离散的子系统，连续子系统与离散子系统相互耦合是典型的混杂系统。基于混杂系统理论的系统模型同时包含系统连续时间变量和离散状态量，且不需要对系统模型近似处理，相对传统建模方法能够更精确描述双向ICPT 系统。基于混杂系统理论的系统建模方法主要有混杂自动机模型、混杂Petri 网模型以及混合逻辑动态（MLD）模型等。目前基于混杂系统理论的建模方法在电力电子领域的应用主要集中于对开关变换器的研究。文献［13］针对Buck 变换器提出了一种基于模式选择的混合逻辑动态模型和控制方法，使变换器可以同时工作在电流连续模式（CCM）和断续导电模式（DCM）这2种工作模式下。文献［14］运用混杂系统理论建立了4阶零电压准谐振变换器在CCM 下的混杂自动机模型，并提出了一种基于比例积分（PI）调节器的有限状态机（PSM）控制策略；文献［15］对单向多负载ICPT 系统建立了混杂自动机模型并对系统不同工作模态进行了稳定性分析。综上，传统建模方法在对双向ICPT 系统建模过程中或采用平均模型忽略了系统的高频特性，或经线性化处理忽略了系统的非线性部分，不能得到系统的精确模型。因此，基于混杂系统理论对双向ICPT系统建模显得尤为必要。

目前对双向ICPT 系统的功率控制主要基于脉冲宽度调制（PWM）、移相（PS）、脉冲频率调制（PFM）。目前该领域的理论研究多以移相为主，但是移相控制会造成开关器件硬开关、直流电压纹波大、启动与功率传输模式切换时电流波动大等问题［16］。文献［17］建立了双向ICPT 系统的功率数学模型，并提出一种相角控制算法，实现了对系统功率方向和大小的调节。文献［18］分析了双向ICPT系统3 个控制自由度对系统变换器开关器件运行状态和传输效率的影响，并提出了一种可实现双向ICPT 系统效率优化的多自由度协调组合控制策略。文献［19］基于扰动观测法提出一种新型控制策略，在不外加电路的条件下，实现了系统不同工况下的相位同步和最大效率点跟踪。综上，目前实现对双向ICPT 系统功率控制主要以移相控制为主，而现有移相控制研究主要集中在对开关器件软开关设计和系统效率优化等方面，对系统启动和功率传输模式切换造成的电流波动问题研究较少。

本文基于稳态模型分析了双LCC型补偿拓扑双向ICPT 系统的谐振拓扑特性，给出了双向ICPT 系统变换器运行过程中各开关器件不同工作状态所对应的工作模态。基于混杂理论建立了双向ICPT 系统的混杂自动机模型，根据系统连续状态量与各工作模态之间的关系，确定了系统离散状态模式切换的边界条件，并设计了混杂控制策略。最后通过MATLAB／Simulink仿真验证了该模型的可行性。

1 双LCC 型补偿拓扑双向ICPT 系统的特性及运行状态分析

1.1 双LCC型补偿拓扑双向ICPT系统拓扑特性分析

双LCC 型补偿拓扑的双向ICPT 系统结构如图1 所示。图中：V1、V2分别为一、二次侧直流电压源；S1—S4组成一次侧H 桥；S5—S8组成二次侧H 桥；D1—D8分别为S1—S8的反并联二极管；u1、u2分别为一、二次侧H桥输出电压；iLf1、iLf2分别为一、二次侧谐振回路中电流；Lf1、Lf2分别为一、二次侧补偿网络的补偿电感；C1、C2和Cf1、Cf2分别为一、二次侧补偿网络的串联和并联补偿电容；L1、L2分别为一、二次侧线圈自感；M为一、二次侧线圈间互感；R1、R2分别为一、二次侧补偿网络的等效电阻。

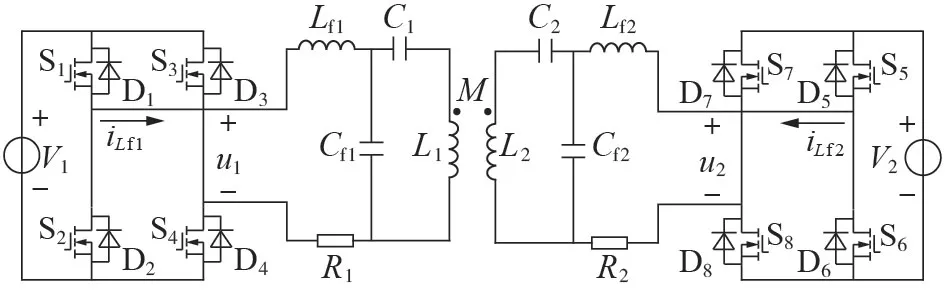
图1 双LCC型补偿拓扑的双向ICPT系统结构Fig.1 Structure of bidirectional ICPT system with dual LCC-typed compensation topology

为简化分析过程，忽略补偿网络电压、电流的高次谐波分量以及网络中各元件的寄生电阻和开关损耗，可得图2 所示双向ICPT 系统的简化电路模型。图中：U1、U2和ILf1、ILf2分别为一、二次侧H 桥输出电压基波分量和输出电流的有效值；I1、I2分别为一、二次侧线圈电流的有效值；Ups、Usp分别为一、二次侧线圈中的感应电压。

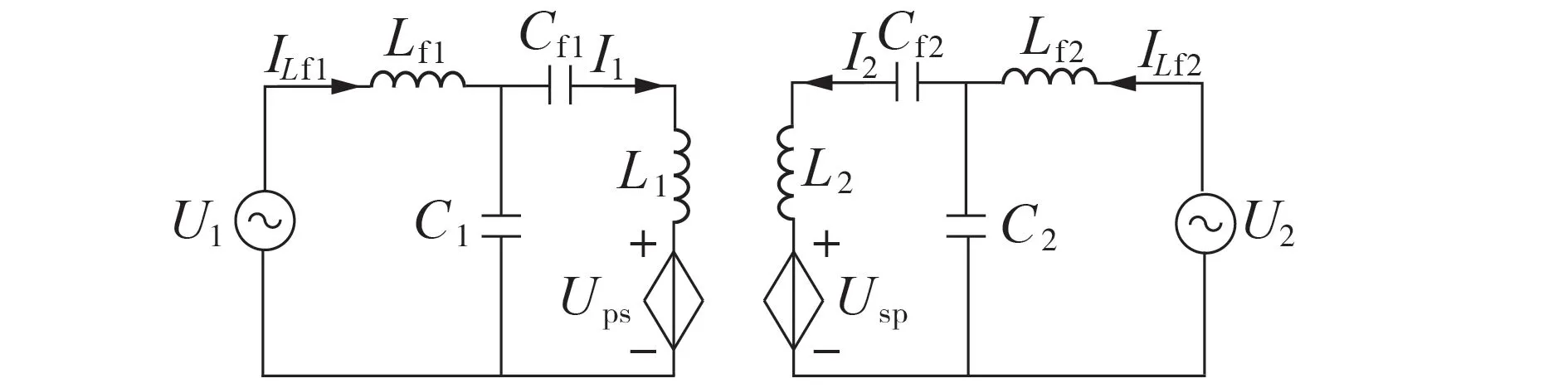
图2 双向ICPT系统的简化基波近似法模型Fig.2 Simplified fundamental harmonic approximation model of bidirectional ICPT system

利用基波近似FHA（Fundamental Harmonic Approximation）法和基尔霍夫电压定律得到双向ICPT系统的有功功率和无功功率［20］为：

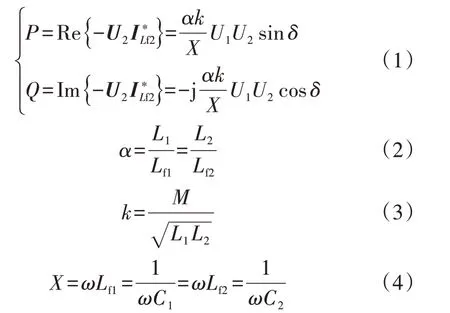
式中：ω为系统工作角频率；δ为一、二次侧H 桥控制信号间的外移相角；U2为二次侧H 桥输出电压的基波相量；I*Lf2为二次侧H 桥输出电流的基波相量的共轭值。

利用傅里叶级数展开，得到一、二次侧H桥输出电压基波分量的有效值为：

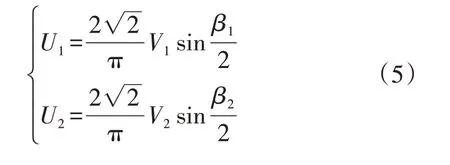
式中：β1、β2分别为一、二次侧H 桥控制信号的内移相角。由式（1）—（5）可得，双LCC 型补偿拓扑双向ICPT 系统的功率传输方向由δ决定：当δ∈［0，π）时，系统功率由一次侧向二次侧传输；当δ∈（-π，0）时，系统功率由二次侧向一次侧传输；且当δ=±π/2 时，系统传输有功功率最大，无功功率最小。同时有功功率的幅值还与一次侧和二次侧H桥的基波电压有关，可以通过β1和β2来调节。

1.2 双向ICPT系统变换器运行状态分析

规定双向ICPT 系统功率从一次侧向二次侧传输为正向功率传输模式，反之为反向功率传输模式。本文选取双LCC 型补偿拓扑，一次侧与二次侧补偿拓扑为对称结构，故正向功率传输模式与反向功率传输模式下系统工作状态相类似，以正向功率传输模式为例，图3 为双LCC 型补偿拓扑双向ICPT 系统开关信号S1—S8和状态量的工作波形图。忽略开关损耗和死区影响，为使系统传输功率最大，正向功率传输模式下一次侧H 桥为逆变网络，二次侧H 桥为整流网络，取β1=β2=π，δ=π/2；反向功率传输模式下一次侧H桥为整流网络，二次侧H桥为逆变网络，取β1=β2=π，δ=-π/2。

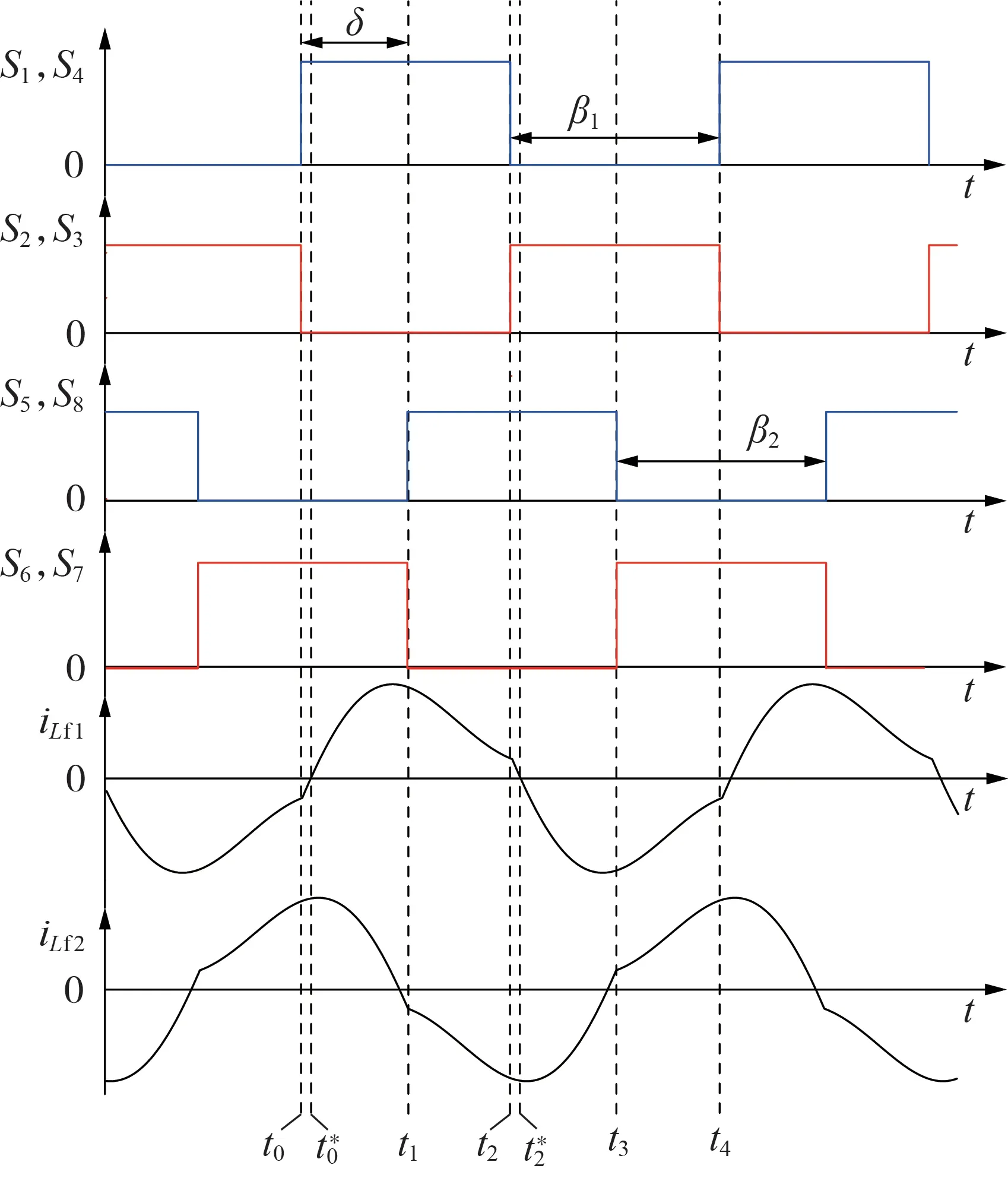
图3 双向ICPT系统开关信号和状态量的工作波形Fig.3 Working waveforms of switching signals and state of bidirectional ICPT system

如图3 所示，双向ICPT 系统正向功率传输模式的一个切换周期分为4种工作模态。

1）工作模态1：t∈［t0，t1］阶段。此时开关器件的工作状态如附录A 图A1（a）、（b）所示。在t0时刻之前，一次侧谐振电流iLf1为负，且流经开关管S2、S3；二次侧谐振电流iLf2为正，且流经开关管S6、S7。在t0时刻，开关管S1、S4收到驱动信号导通，iLf1为负，反并联二极管D1、D4导通续流；t*0时刻iLf1负向减小至0，开关管S1、S4以零电压开关（ZVS）方式导通，iLf1开始正向增大。该工作模态下，一次侧串联补偿电容C1反向充电，二次侧串联补偿电容C2正向放电。

2）工作模态2：t∈（t1，t2］阶段。此时开关器件的工作状态如附录A 图A1（c）所示。一次侧各开关管工作状态与工作模态1 下相同；t1时刻，开关管S6、S7关断，S5、S8导通，全桥整流电路输出电压u2为V2，谐振电流iLf2负向增大。该工作模态下，一次侧串联补偿电容C1反向放电，二次侧串联补偿电容C2反向充电。

3）工作模态3：t∈（t2，t3］阶段。此时开关器件的工作状态如附录A 图A1（d）、（e）所示。t2时刻，一次侧开关管S1、S4关断，一次侧谐振电流iLf1为正，故反并联二极管D2、D3导通续流；t*2时刻iLf1减小至0，续流二极管D2、D3实现零电流开关（ZCS）关断，开关管S2、S3实现ZVS 导通，iLf1开始负向增大；二次侧各开关管工作状态与工作模态2 下相同。该工作模态下，一次侧串联补偿电容C1正向充电，二次侧串联补偿电容C2反向放电。

4）工作模态4：t∈（t3，t4］阶段。此时开关器件的工作状态如附录A 图A1（f）所示。一次侧各开关管工作状态与工作模态3 下相同；t3时刻，二次侧开关管S5、S8关断，S6、S7导通，全桥整流电路输出电压u2为-V2，谐振电流iLf2正向增大；一次侧串联补偿电容C1开始正向放电，二次侧串联补偿电容C2正向充电。

2 双向ICPT 系统的混杂自动机建模及控制策略

2.1 双向ICPT系统的混杂自动机模型建立

由前文对双向ICPT 系统的运行状态分析可知，双向ICPT 系统的功率传输过程中对应多种工作模态。其中每一种工作模态均可看作一个离散状态模式，而单个工作模态中系统变量又受相应的微分方程约束连续变化，形成一个连续动态系统。双向ICPT 系统工作过程中连续子系统与离散子系统相互耦合，体现了系统的混杂特性。

根据混杂自动机理论，双向ICPT 系统的混杂自动机模型可表示为函数H（Q，X′，Sint，F，I，E，G），其中：Q={qi|i=z，f，1，2，3，4} 表示系统离散状态模式的有限集合，根据功率传输方向，系统可分为正向功率传输模式qz和反向功率传输模式qf，每种传输模式中根据开关管的导通状态又可将其分为4 个离散状态模式q1—q4；X′表示系统连续状态空间；Sint表示系统的初始状态量集合；F表示系统离散状态量与连续状态量之间的函数映射；I表示系统各离散状态模式下连续状态量的不变集合；E表示系统各离散状态模式的切换集合；G表示系统各离散状态模式切换条件的集合，如Gij（i，j=z，f，1，2，3，4）表示系统从qi切换至qj的切换条件。令离散状态模式q1—q4下开关管S1—S8所对应的开关信号S1—S8满足式（6）所示关系，且4 种离散状态模式下开关管的工作状态见表1。

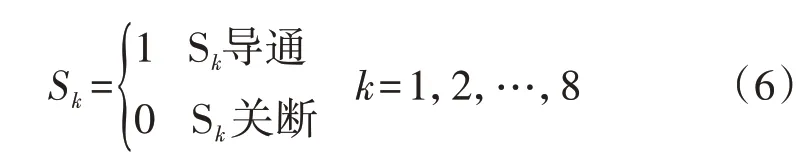
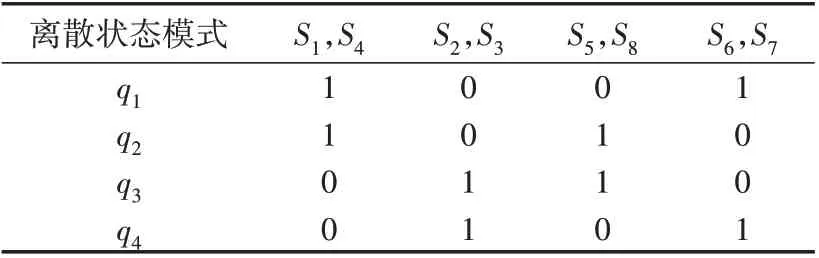
表1 各离散状态模式下开关管工作状态Table 1 Operating states of switches under each discrete state mode

选取系统的输入量为u(t)=［V1，V2］T，系统连续状态量为x(t)=［iLf1，i1，uCf1，uC1，iLf2，i2，uCf2，uC2］T（i1、i2分别为流经系统一、二次侧线圈L1、L2的电流；uCf1、uCf2分别为系统一、二次侧并联补偿电容Cf1、Cf2两端电压；uC1、uC2分别为一、二次侧串联补偿电容C1、C2两端电压）。则双向ICPT 系统各离散状态模式的状态空间方程为：

式中：Δ=M2-L1L2；m、n的取值如表2所示。

表2 各离散状态模式下m、n的取值Table 2 Value of m and n under each discrete state mode

双向ICPT 系统的离散状态模式切换集合包括：系统功率传输模式的离散状态模式切换集合E0=｛（qz，qf），（qf，qz）｝；系统正向功率传输模式下的离散状态模式切换集合E1=｛（q1，q2），（q2，q3），（q3，q4），（q4，q1）｝；系统反向功率传输模式下的离散状态模式切换集合E2=｛（q1，q4），（q4，q3），（q3，q2），（q2，q1）｝。

2.2 双向ICPT系统的混杂控制策略

双向ICPT 系统混杂自动机模型的建立，使其控制问题等效为系统正、反向功率传输模式的切换和单一模式中各离散状态模式的切换问题，即各离散状态模式间切换条件的确定和选择。正向功率传输模式下，双LCC 型补偿拓扑的电感电流和电容电压波形如图4 所示。图中，IL2为正向功率传输模式下工作模态3 与工作模态4 交界处二次侧谐振电流值；-IL2为正向功率传输模式下工作模态1 与工作模态2交界处二次侧谐振电流值。

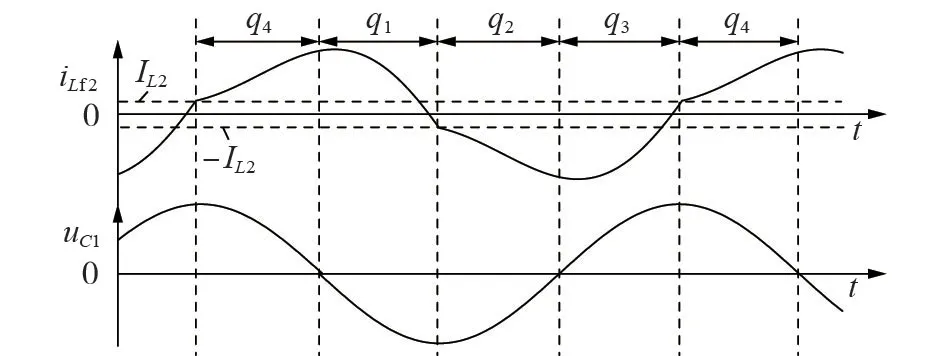
图4 正向功率传输模式下电感电流和电容电压波形Fig.4 Waveforms of inductor current and capacitor voltage under forward power transfer mode

正向功率传输模式下各离散状态模式切换控制策略如下。

1）离散状态模式q1→离散状态模式q2的切换条件G12为：

4）离散状态模式q4→离散状态模式q1的切换条件G41为：

系统切换过程如附录A图A2所示。

3 仿真分析

为验证所提双向ICPT 系统混杂自动机模型及混杂控制策略的可行性，本文在MATLAB／Simulink中搭建了双LCC 型拓扑双向ICPT 系统仿真模型，如附录A 图A3所示。模型一、二次侧直流输入电压为280 V，一、二次侧线圈自感为312 μH，开关工作频率为90 kHz，其他参数值可根据文献［6］所给公式计算求得，如附录A表A1所示。

为了验证基于混杂自动机模型的双向ICPT 系统控制策略在正、反向功率传输模式下各工作模态能够稳定、有序发生切换，对双向ICPT 系统正向功率传输模式与反向功率传输模式下变换器开关信号及一、二次侧的谐振电流进行仿真。图5、附录A 图A4 分别为双向ICPT 系统在正、反向功率传输模式下变换器开关信号和一、二次侧谐振电流的仿真波形。由仿真波形可知，本文所建立双向ICPT 系统混杂自动机模型在一个控制周期内，正向功率传输模式下，各个离散状态模式的切换顺序为q1→q2→q3→q4→q1，系统进入周期循环稳定工作；反向功率传输模式下，各个离散状态模式切换顺序反之。且谐振电流波形与理论分析相符。仿真结果验证了该模型在正、反向功率传输模式下各离散状态模式能够按预期设计有序切换，得到稳定的输出电流。

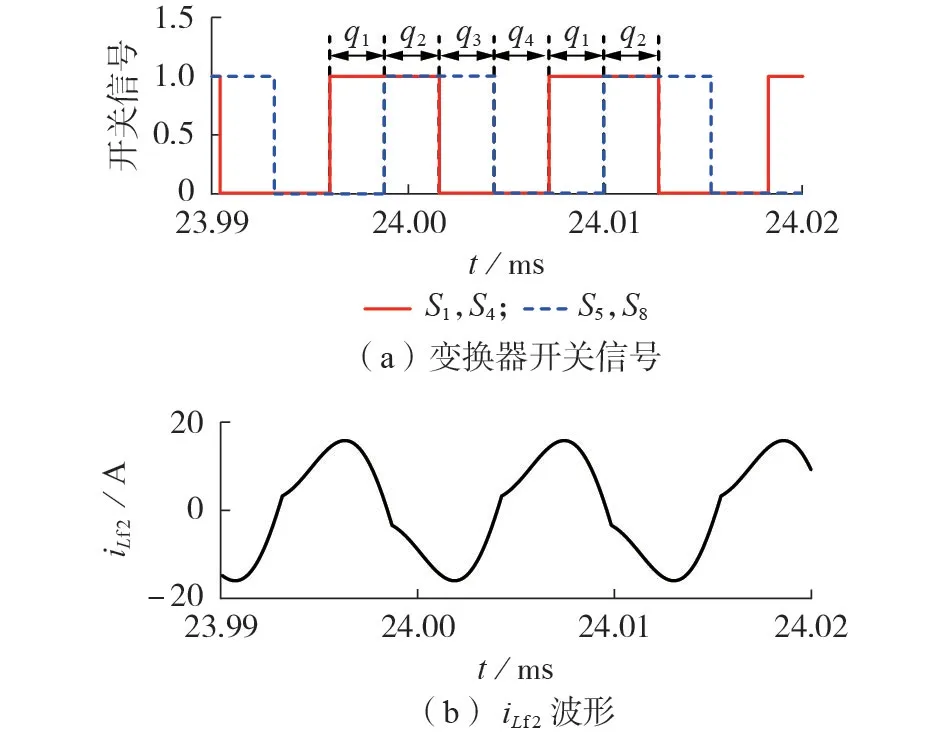
图5 正向功率传输模式下双向ICPT系统仿真波形Fig.5 Simulative waveforms of bidirectional ICPT system under forward power transmission mode

在t=0.05 s 时刻，改变Stateflow 模块的外加触发信号sps，以此控制双向ICPT 系统的功率传输模式切换。图6为双向ICPT系统二次侧有功功率切换仿真波形图，其中图6（a）为正向功率传输模式向反向功率传输模式切换的系统二次侧有功功率仿真波形，图6（b）为反向功率传输模式向正向功率传输模式切换的系统二次侧有功功率仿真波形。由仿真结果可知，系统有功功率在0.05 s 发生换向，即系统正、反向功率传输模式正常切换，且能够快速达到稳定运行状态。仿真结果表明本文所提混杂控制策略能够实现双向ICPT系统功率传输模式稳定切换。

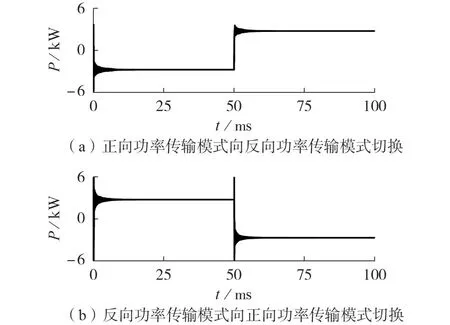
图6 功率传输模式切换时二次侧有功功率仿真波形Fig.6 Simulative waveforms of active power at secondary side during power transmission modes switching

为了验证基于混杂自动机模型的系统控制策略对双向ICPT 系统启动及功率传输模式切换时电流波动的抑制作用，将所提混杂控制策略与传统移相控制方法进行对比。对于移相控制，取正向功率传输模式下β1=β2=π，δ=π/2，反向功率传输模式下β1=β2=π，δ=-π/2，开关器件的开关频率fs设为90 kHz。对于本文基于混杂自动机模型的混杂控制策略，正向功率传输模式下，双向ICPT 系统的混杂自动机控制逻辑由式（10）—（13）确定，反向功率传输模式下，双向ICPT 系统的混杂自动机控制逻辑由式（14）—（17）确定；双向ICPT 系统正、反向功率传输模式间切换的混杂自动机控制逻辑由式（18）、（19）确定。2种控制策略下系统二次侧谐振电流和有功功率仿真波形对比分别如图7、附录A 图A5 所示。仿真结果表明，系统稳定运行时，2 种控制方法所对应的系统二次谐振电流及有功功率波形基本重合，当系统发生启动、功率传输模式切换时，采用所提控制策略，系统二次侧谐振电流及有功功率的波动范围较传统移相控制有明显减小，更有利于系统稳定运行。

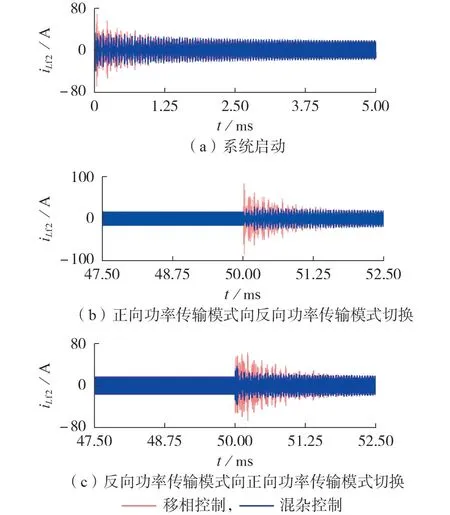
图7 二次侧谐振电流仿真波形对比Fig.7 Comparison of simulative waveforms of resonant current at secondary side

4 结论

本文对双向ICPT 系统建立了混杂自动机模型，分析了系统连续状态变量与离散状态模式之间的耦合关系，得到系统各离散状态模式切换的边界条件，实现了对系统不同功率传输模式及其各离散状态模式的控制。与传统的建模方法相比，双向ICPT 系统的混杂自动机模型未对其离散模型做任何近似处理，能够更准确地描述双向ICPT 系统的动态特性，模型精度高。同时基于混杂自动机模型设计的控制器，将系统的控制问题转换为各离散状态模式边界条件的选择问题，对双向ICPT 系统的连续变量与离散状态模式进行统一控制且有效改善了系统启动及不同功率传输模式切换所引起的电流波动现象，控制层次清晰，方法简单。仿真结果表明，一个控制周期内双向ICPT 系统各工作模态有序切换，且能够实现双向ICPT 系统的正、反向功率传输模式切换。同时基于混杂自动机模型的系统控制策略能够有效抑制系统启动及不同功率传输模式切换时的电流波动，有利于双向ICPT 系统稳定运行，从而验证了该方法的可行性。

附录见本刊网络版（http：//www.epae.cn）。