不同解算策略对GPS 坐标序列噪声模型建立及速度影响

付杰，聂启祥，贺小星，陈红康，郇常敏

(1.华东交通大学 土木建筑学院,南昌 330013；2.江西理工大学 土木与测绘工程学院,江西 赣州 341000；3.东华理工大学 测绘工程学院,南昌 330032)

0 引言

随着GPS 在各领域内应用的不断加深，国内外学者设计开发了对应的GPS 数据处理软件.GAMIT软件作为UNIX 体系的开源软件，该软件以双差法处理GPS 观测数据，从而消除了卫星钟差和接收机钟差的影响，有速度快、更新周期短、精度高等优点，被广泛地应用于GPS 数据处理中[1].而Bernese 软件不仅可以处理双差数据，还可以额外处理非差数据，从而导致解算出来的结果，和其他软件的结果有一定的差异.

针对不同解算策略对GPS 站速度估计影响，文献[2]对GAMIT 和GISPY 软件所解算GPS 站速度场进行比较，指出约2/3 的测站速度差值在2～6 mm/a 之间.文献[3]运用GAMIT/GLOBY 和Bernese解算方法对土耳其连续运行参考站(CORS)进行对比分析，发现它们在北(N)、东(E)、天顶(U)三个方向上的日重复度几乎是一致的，但GAMIT/GLOBY比Bernese 给出了更大形式误差.因此，解算策略的变化会对数据的估算结果产生一定的影响.此外，有实验采用多个噪声模型来分析国际GNSS 服务(IGS)站的最佳模型[4]，发现IGS 站坐标时间序列的最优模型呈现出多样性，并会对速度及速度不确定度产生不可忽略的影响.文献[5]估计了在两种噪声模型条件下的GPS 站的速度既不确定性，发现水平方向最大影响量级为0.3 mm/a，垂直方向最大影响量级为0.8 mm/a.因此，如果不考虑有色噪声，会严重低估最终参数估计的真实不确定性.而且已有的研究并未对软件的联合解算策略进行分析，且多数实验分析所选站点数量较少，时间序列长度较短，在进行不同解算策略速度分析时，也并未考虑到有色噪声对速度估计的影响.

因此，为了探究在有色噪声背景下和不同解算策略下GPS 噪声模型特性，以及对GPS 速度及速度不确定度的影响情况，本文选取白噪声+闪烁噪声(WN+FN)、高斯马尔科夫(GGM)+WN、幂律噪声(PL)+WN和随机漫步噪声(RWN)+FN+WN 四种噪声模型，以赤池信息量准则/贝叶斯信息量准则(AIC/BIC)为基础，分别使用GAMIT、Bernese 及联合解算策略(Comb)，对中国大陆构造环境监测网络(陆态网)121 个GPS基准站时间序列进行计算分析.

1 GPS 时间序列获取与预处理

为分析不同解算策略下GPS 时间序列噪声模型的影响，本文以陆态网的部分站点作为研究对象.站点选取采取策略如下：1)站点位置分布均匀，不宜过近；2)在所选时段2011—2019 年间运行良好；3)数据缺失率不高于10%，如表1 所示.最终选取站点共计121 个，站点分布情况如图1 所示.

图1 站点分布图

表1 数据缺失率统计表 %

2 GPS 坐标时间序列模型建立

2.1 GPS 噪声模型估计

已有研究表明GPS 坐标时间序列噪声模型主要可以描述为WN、FN、PL 和RWN 三种[6-7]，或者它们的组合模型，其协方差矩阵可表示为：

式中：a为WN 振幅；I为单位矩阵；b为有色噪声(CN)振幅；J表示为CN 的协方差矩阵.此外，除了上述模型，有研究指出部分站坐标序列可以用GGM 模型来描述[8]，且GGM 模型获得的速度不确定度较小，因此本文额外选取WN+GGM 模型进行估算.

2.2 最优模型估计准则

频谱分析法和最大似然估计(MLE)法是如今最常用的两种噪声分析方法[9-10]，前者以频率域对时间序列中存在的噪声特性进行分析，可以直接地反映出噪声模型的基本特性，但此方法过于依赖频谱均匀，对于数据缺失率较高的数据进行处理时，会导致估算出来的结果不准确.而MLE 方法则避开了频谱法的缺陷，与频谱法不同的是，该方法是在时间域中对时间序列的噪声进行估计，从而对不同的噪声模型进行评估，并以此计算出极大似然对数值，该数值越大，估算出来的结果越可靠.但MLE 方法也有一定的局限性，当所估算的噪声模型参数较多时，计算出的极大似然对数值也会偏大[11].

为了更有效地对噪声模型进行估计，国外学者提出了基于赤池信息量准则/贝叶斯信息量准则(AIC/BIC)噪声模型的估计方法[12-13].AIC/BIC 方法顾及了模型参数的影响，并采用两个指标来进行评估，一定程度上弥补了MLE 法的缺陷，其原理如下[14]：

式中：L为某一模型下的似然参数；k为所拟合模型中参数的数量；n为观测值数目.当AIC 和BIC 计算结果不一致时，选取两者数值更小的作为最优噪声模型.

2.3 速度不确定度估计

针对不同噪声模型对站速度不确定估计的影响，文献[15-16] 给了有色噪声背景下GPS基准站坐标时间序列速度不确定估计的函数模型

式中：g为每年观测数；T为观测周期；a和b为常数，a=1.78，b=0.22；σWN，σFN和 σRWN为WN、FN、RWN速度不确定度.

3 不同解算策略实验分析

3.1 不同解算策略下GPS 站噪声模型特性分析

对所选陆态网下121 个GPS基准站采用FN+WN、GGM+WN、PL+WN 和FN+RWN+WN 噪声模型，并采用AIC/BIC 最小的评价准则进行计算分析，表2为3 种解算方法在E、N、U 方向量的最优模型统计结果，表3 为不同解算策略之间最优模型发生改变的站点数统计.

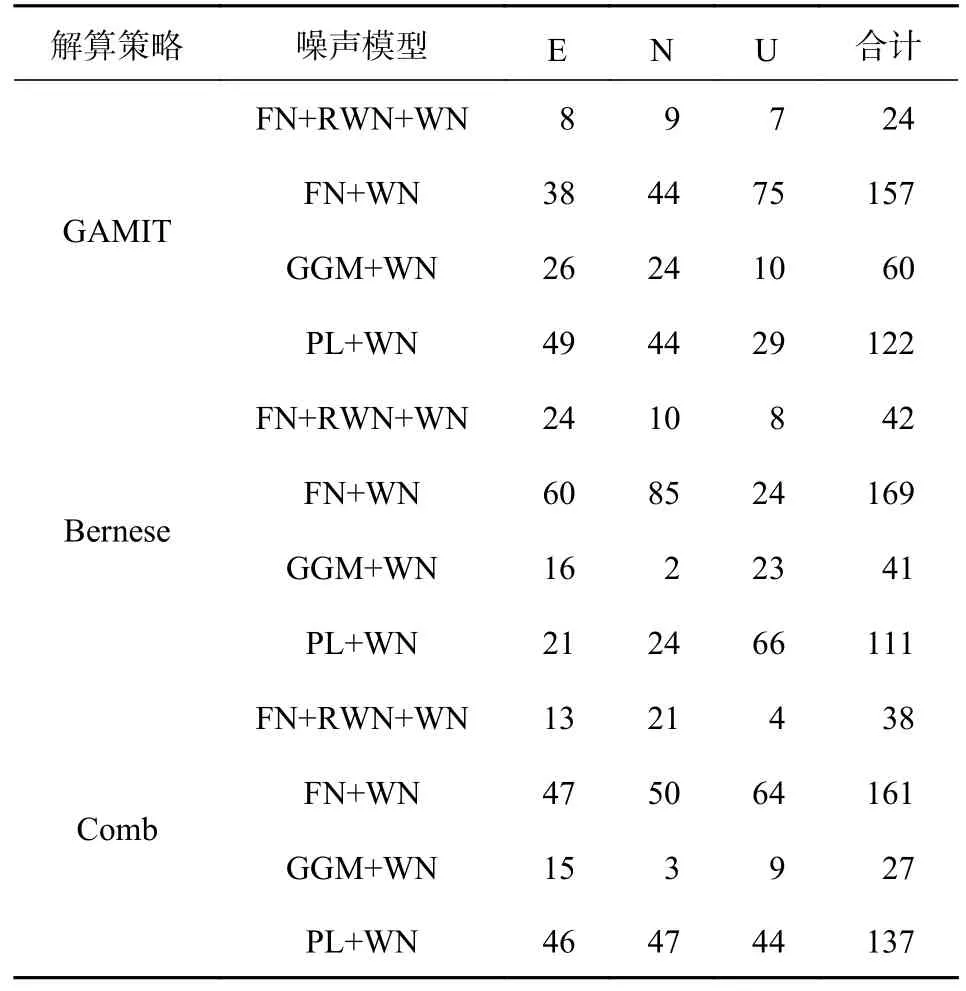
表2 噪声模型测站数估计结果

表3 不同解算策略下噪声模型测站改变量

由表2 可知，在E、N 两个方向分量中，GAMIT 解算策略的最优模型比例非常相近，主要表现为FN+WN 和PL+WN 模型特性，FN+RWN+WN 模型的占比极低.Bernese 解算结果则有所不同，在E 方向分量中FN+WN 和FN+RWN+WN 最优模型的比例上升，而另外两种噪声模型的测站数有所下降.但N 方向分量中，表现出FN+WN 模型特性的站点数上升更为显著，而GGM+WN 最优模型特性的站点数有所下降.坐标U 方向分量中，GAMIT 和Bernese 解算策略分别主要表现为FN+WN(75)和PL+WN(66)模型特性，随着解算策略的改变，Bernese 解算结果中PL+WN 模型特性的站点数上升明显.Comb 解算策略则一定程度上，整合两种解算策略在噪声模型上的特点，呈FN+WN 和PL+WN 模型特性测站数分别为64 和44.而表3 中显示，在三种解算策略的最优模型特性改变量中，Comb 与 GAMIT 解算结果中模型特性的改变量是最低的，即Comb 与 GAMIT 解算结果更为相似，不同的是Comb 解算策略中FN+RWN+WN最优模型占比上升，GGM+WN 最优模型占比下降.由此可得：三种解算策略中表现出最优模型占比最高的都为FN+WN 模型，其次为PL+WN 模型，FN+RWN+WN 和GGM+WN 模型占比较少；其次，GAMIT 解算策略在E、N 方向分量中主要表现为FN+WN 和RWN+WN 模型特性，Bernese 解算策略则更容易表现为FN+WN 模型特性，坐标U 方向分量中，GAMIT 和Bernese解算策略主要表现为FN+WN 和PL+WN 模型；第三，相对于Bernese 解算策略，GAMIT 解算策略估计结果和Comb 解算策略噪声模型估计结果更为相近.

3.2 不同解算策略对GPS 速度的影响

为进一步探究解算方法对GPS 速度的影响，本文以所测最优模型为基础，对三种不同的解算策略进行E、N、U 方向分量的速度估计，并以此作图(限于篇幅，仅列出15 个站点进行分析).

由图2 可知，不同解算策略对E、N 方向分量的速度影响较小，对U 方向分量的影响较大.由于三个方向速度差异较大，无法直观地从图中表现出更细致的数值情况.本文以Comb 解算方法估计结果为基础，将另外两种解算方法与其分别求差，统计结果如表4 所示.

表4 不同解算策略下差值极值 mm·a-1

图2 不同解算策略下E、N、U 方向分量速度

在GAMIT 和Comb 解算策略差值计算中，E、N、U 三方向下分别有66.7%、93%、53%的站点速度差值低于0.1 mm/a，而Bernese 和Comb 解算下，只有53%、6.7%、0%的站点速度差值小于0.1 mm/a，速度差统计结果如表4 所示，GAMIT 与Comb 解算策略中均值最大为0.137 mm/a，最小为0.050 mm/a，而Bernese 与Comb 解算策略的均值最大值和最小值都超过了GAMIT 与Comb 的差均值.因此，Bernese 相对于Comb 解算策略所计算的差值都更为偏大.此外，从方向上进行分析，在E、U 方向分量中，Comb与GAMIT 和Bernese 求差的均值较小，而在U 方向分量中，所测站点的速度差相对与E、N 方向上升较大，Bernese 与Comb 的差值结果则更为明显，最小的E 方向均值仅为0.112 mm/a，最大的U 方向中均值达到0.819 mm/a.依据上述分析可得，相对于Bernese 解算策略，GAMIT 解算策略对Comb 的所计算出的结果改变会更小，且不同结算策略在U 方向分量上的影响更为显著.

3.3 不同解算策略对GPS 速度不确定度的影响

为了深入分析解算策略对速度不确定度的影响，以Comb 方法为基准，将另外两种解算策略计算结果与其求差，3 种解算策略速度不确定度差值规律变化曲线(仅列出50 个站点)，具体如图3 所示.

由图3 可知，不同解算策略对速度不确定度具有一定的影响.在GAMIT 和Comb 解算策略下，E、N、U 三坐标分量上约34%、36%、52%的站点速度不确定度差值大于0.1mm/a，Bernese 和Comb 解算策略下，E、N、U 坐标分量上40%、40%、54%的站点速度不确定度差值大于0.1 mm/a，说明E、N 方向上解算策略的改变所造成的速度不确定度影响比较接近，并且U 方向比E、N 方向对速度不确定度的影响更大.此外，在所选站点中，E 方向速度不确定度差值最大的站点为HETS，约为0.854 mm/a，N 方向最大的时JLCB 站，为1.057 mm/a，而U 方向的速度不确定度差值最大的是JXHK，达到3.268 mm/a，陆态网所提供的部分基准站在垂直方向上受地壳构造和非构造形变的影响，所以导致在该方向上的速度不确定度偏离正常水准，并且在对流层和电离层的影响下，所计算的垂直速度精度会出现一定的下降，所以在U 方向上的速度不确定度差值则会有一定程度的上升.由此可以看出：和速度估算结果类似，解算策略的改变对速度不确定度在E、N 方向具有一定的影响，在U 方向上变化更为显著.

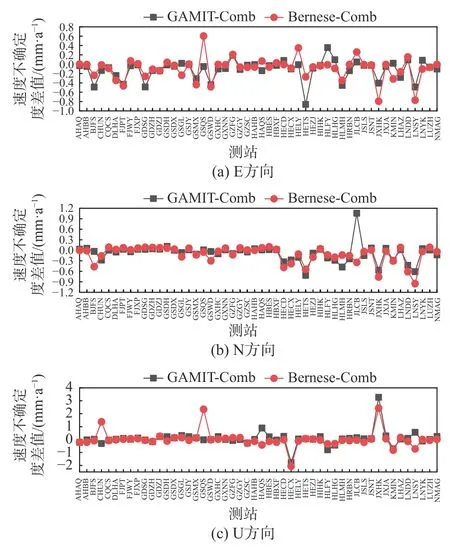
图3 不同方向下速度不确定度差值

4 结论

本文以陆态网121 个GPS基准站为研究对象，采用GAMIT、Bernese 和GAMIT/Bernese 联合解算方法，并结合FN+WN、PL+WN、GGM+WN 和FN+RWN+WN 总计四种噪声模型，以此探讨不同解算策略对GPS 站噪声模型以及速度不确定度的影响，得出以下结论：

1)所选121 个GPS基准站主要表现为FN+WN和PL+WN 噪声特性，且解算策略的改变在不同方向上会出现一定的差异，在E、N 方向上，GAMIT 软件主要表现为FN+WN 和RWN+WN 模型特性，Bernese则更容易表现为FN+WN 模型特性.在U 方向上，GAMIT 解算结果显示，表现出FN+WN 噪声模型特性的站点会有一定程度的上升，而Bernese 解算结果则主要表现为PL+WN 噪声模型.Comb 解算结果相对于GAMIT 解算结果差别较小.

2)解算策略对速度及速度不确定度的影响较为相似，在E、N 方向上较小，在U 方向上较大；在所测站点的速度估计中，速度差均值最大达到0.819 mm/a，在Bernese 和Comb 解算下，速度在N、U 方向上差值较大，只有6.7%、0%的站点速度差值小于0.1 mm/a.而在速度不确定度估计中，E、N 方向速度不确定值差值大于0.1 mm/a 的站点数较为接近，GAMIT 和Comb 解算策略下为34%和36%，Bernese 和Comb解算策略下为40%.而U 方向存在超过50%的站点速度不确定值大于0.1 mm/a，最大的为JXHK，达到3.268 mm/a.从速度及速度不确定度估算结果可以得出，Comb 解算结果和GAMIT 解算结果更为接近.