与 的上下极限之间的关系及其应用

王 霞 , 马晓雯

(1.北京工业大学 理学部统计与数据科学学院, 北京 100124；2.齐鲁师范学院 数学学院, 山东 济南 250200)

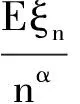
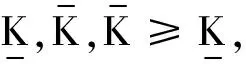
证明:由于

若能证得

(1)

则

往证(1)式.

因为

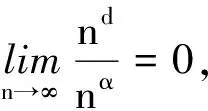
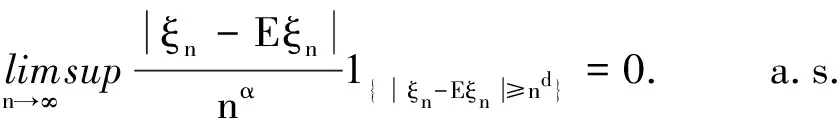
即证

(2)

由概率的从上连续性[4-5]

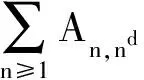
2 应用

在给出应用前, 我们先给出如下引理.

引理设X1,X2,…,Xn为独立的随机变量序列.∀i=1,2,…,n,E(Xi)=0, |Xi|≤bi,a.s..则

∀x>0,

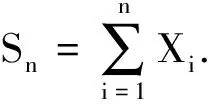
证明:首先我们给出如下事实:

∀h∈,

(3)

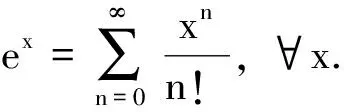
故

即

又因为

(2n)!=2n·(2n-1)···(n+1)n!≥2·2…2·n!=2n·n!,

所以

故(3)式得证.

接下来, 我们给出另一事实: 对于均值为 0 的随机变量X, 假设|X|≤b,a.s., 则对∀h∈,

(4)

现证(4)式.对于∀h∈,ehx是x的凸函数, 则

因为E(X)=0, 且利用(3)式得

故(4)式得证.

最后证明引理.利用 Markov 不等式[6]，对∀h>0,

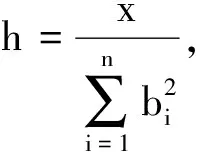
现给出我们的应用.

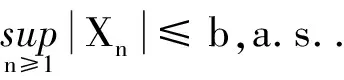
证明:对于Sn, 利用引理有

故结论得证.