公轨两用钢桁梁斜拉桥桥面系横隔板疲劳性能分析

李俊诺

（广东省交通规划设计研究院集团股份有限公司）

0 引言

公轨两用钢桁梁斜拉桥采用桁架作为主梁，其上不能直接通行车辆，需另外增加桥面结构。板桁组合桥面较混凝土桥面、结合梁桥面等结构形式具有桥面自重小、结构形式简洁、能适应桁架较大的节间或横梁距离的优点，在设计中经常被采用[1]。在板桁组合桥面系中，桥面系不仅作为为车辆提供行驶空间的构件，其还作为主桁架结构的一部分参与桁架受力中，计算分析时需要考虑板桁共同作用[2]。

板桁组合桥面系一般由正交异性板、横隔板或横隔梁、纵梁等直接承受车轮荷载的构件组成[3]，设计荷载中活载作用的比例一般较恒载作用大得多，容易产生疲劳破坏。研究表明，传统正交异性钢桥面板中横隔板与U 肋交叉处细节疲劳损伤最为严重，该类细节的疲劳裂纹占钢桥面板所有疲劳裂纹的比例达38.2%[4]。为保证板桁组合桥面系结构在桥梁运营期间的安全性，对桥面系横隔板的疲劳性能进行分析研究具有一定的意义。

1 工程概况

某公轨两用钢桁梁斜拉桥采用半漂浮体系，其孔跨布置为：(77.5+166.1+468+166.1+77.5)=955.2m，主梁为带副桁的板桁结合钢桁梁结构，上层通行8 车道公路交通，下层通行两线轻轨交通，线路中心距为4.8m。主桁架上层桥面宽38.2m，下层桥面宽16m，桁高11.7m，标准节间长度为15.1m，横隔板标准间距为25.167m，如图1 所示。

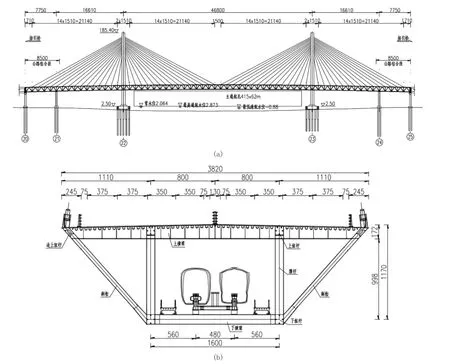
图1 某公铁两用钢桁梁斜拉桥立面图和横断面图

该桥采用板桁组合的桥面结构形式，钢桥面采用U肋加劲，支承于上横梁及上弦杆上。在一个标准节间内，上横梁设置有节点位上横梁横隔板、一般位上横梁横隔板1、一般位上横梁横隔板2 及拉索位上横梁横隔板，如图2 所示。其中板桁组合桥面系钢桥面板厚16mm，上层竖向节点板板厚30mm，上弦杆顶板板肋过焊孔半径为35mm，上弦杆腹板及底板板肋过焊孔半径为30mm，其余过焊孔半径均为50mm，桁架梁各主要构件的截面形状及板厚尺寸见表1。

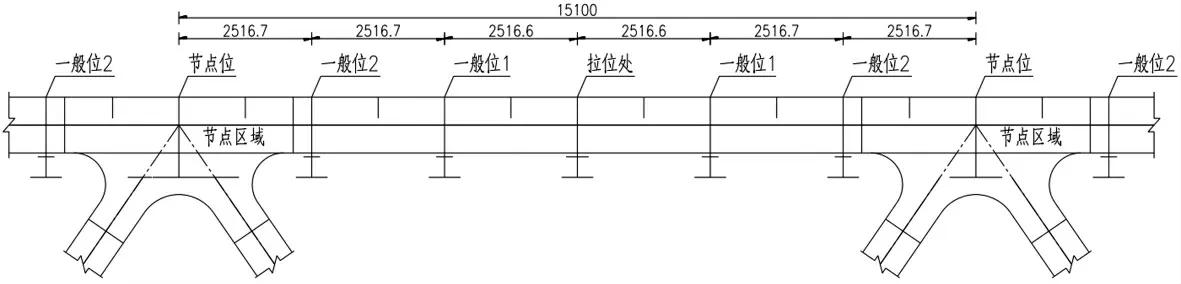
图2 板桁组合桥面系上横梁横隔板立面布置/mm

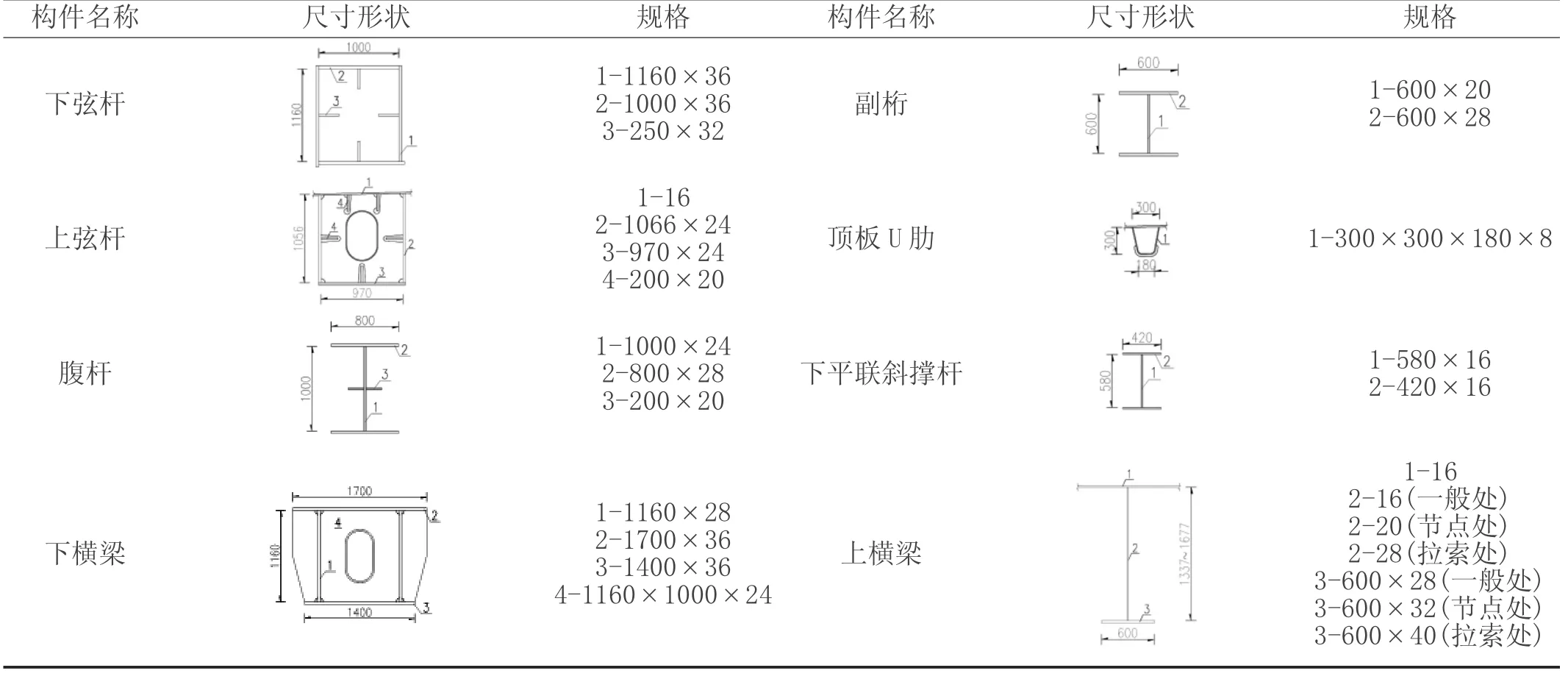
表1 主要构件的截面形状及板厚尺寸(mm)

由于上横梁梁高大于上弦杆梁高，因此在非节点位上横梁与上弦杆相接处采用类似于正交异性桥面板U肋与横隔板间弧形开孔的构造。传统正交异性桥面板横隔板上的开孔能有效降低横隔板与U 肋间的连接刚度，减少横隔板与纵梁连接时焊接造成纵肋底部的应力集中等，但由于开孔导致该处刚度不连续，由此带来新的应力集中问题[5]。本文基于空间板壳有限元模型，对板桁组合桥面系上横梁与上弦杆相交处焊缝(疲劳细节Ⅰ)进行疲劳性能分析，如图3 所示。

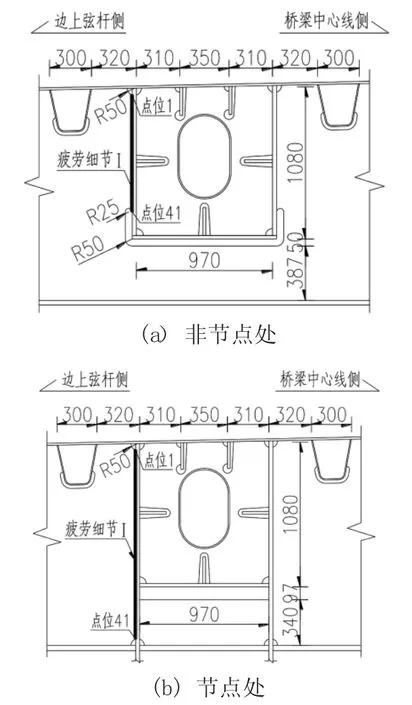
图3 板桁组合桥面系上横梁与上弦杆相交处构造/mm

2 疲劳荷载

根据《公路钢结构桥梁设计规范》[6]，对公轨两用钢桁梁斜拉桥进行疲劳分析需要明确四项内容：

⑴疲劳荷载的确定；

⑵疲劳细节的选择；

⑶针对该疲劳细节出现最大应力幅时疲劳荷载加载位置的确定；

⑷疲劳验算方式的确定。

针对公轨两用钢桁梁斜拉桥，其疲劳荷载包含公路疲劳荷载及轻轨疲劳荷载，两者之间的疲劳组合效应目前已有一定的研究成果，但国内仍无规范可循[7]。

对于疲劳荷载的确定，本文采用1:1 叠加的方式计算，其中公路疲劳荷载采用《公路钢结构桥梁设计规范》[7]中疲劳荷载计算模型Ⅲ；轻轨疲劳荷载根据《铁路桥梁钢结构设计规范》[8]，采用实际运营的轻轨列车编组，其为6 节编组，轴重P 为120kN，如图4 所示。根据文献[8]计算可得，列车冲击系数为1.321，钢梁双线系数为1.18，城际铁路损伤修正系数为1.000，故下层列车加载时的荷载系数为1.321×1.18/1.000=1.559。

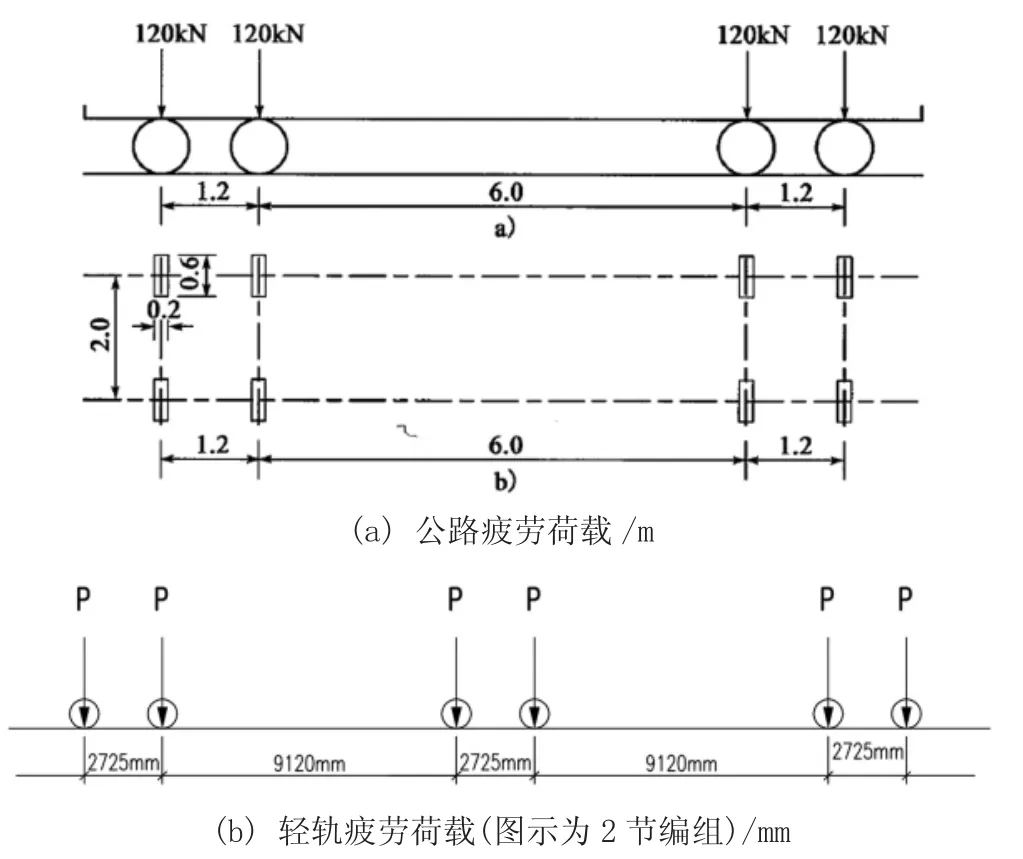
图4 公轨两用钢桁梁斜拉桥疲劳荷载

3 疲劳计算方法

对于图3 中所示的疲劳细节Ⅰ，由于在文献[7]和文献[8]中并没有完全对应的构造细节，因此针对板桁组合桥面系上横梁与上弦杆腹板的连接构造，本文近似选取文献[7]正交异性桥面板开口加劲肋中连续纵肋与横梁连接的构造细节，其细节类别为55。同时，因为文献[7]中对于该构造细节采用等效应力幅评定疲劳性能，所以本文疲劳细节Ⅰ疲劳性能的验算根据式⑴～式⑸计算。

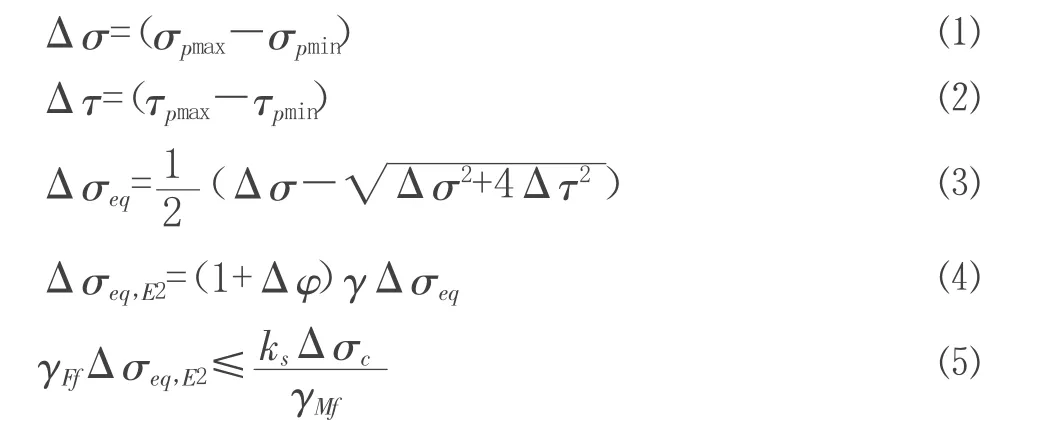
式中：

σpmax、σpmin——疲劳荷载最大及最小正应力幅；

τpmax、τpmin——疲劳荷载最大及最小剪应力幅；

Δσeq——等效应力幅；

Δσeq，E2——按2.0×106次常幅疲劳循环换算得到的等效常值应力幅；

Δφ——放大系数，取0.00；

γ——损伤等效系数，γ=γ1·γ2·γ3·γ4，且γ≤γmax，根据文献[7]计算得，γ1=2.45，γ2=1.55，γ3=1.00，γ4=1.00，γmax=2.17，故取γ=2.17；

γFf——疲劳荷载分项系数，取1.0；

γMf——疲劳抗力分项系数，取1.35；

ks——尺寸效应折减系数，取1.0；

Δσc——疲劳细节类别，取55。

对于疲劳细节Ⅰ出现最大应力幅时，疲劳荷载加载位置的确定，分为公路疲劳荷载最不利位置确定和轻轨疲劳荷载最不利位置确定。对于轻轨疲劳荷载，由于其为纵向一维单线加载，考虑双线效应的方式计算，因此其疲劳细节Ⅰ应力的最不利位置只要作出对应的应力影响线即可得到。对于公路疲劳荷载，由于其为纵横向二维平面加载，因此疲劳细节Ⅰ应力的最不利位置需要按纵横向搜寻的方法确定，一般有两种方式。方式一为先根据横向影响线确定最不利横向位置，再根据纵向影响线确定最不利纵向位置，从而确定最终位置。方式二为采用纵横向遍历时程加载，先作出疲劳细节Ⅰ的横向应力时程曲线确定横向最不利位置，再作出该疲劳细节的纵向应力时程曲线确定纵向最不利位置，从而确定最终位置。虽然上述两种搜寻方法在具体计算形式上有所差异，但本质上都是在求解该疲劳细节在桥面系上的应力影响面。

针对公轨两用钢桁梁疲劳荷载最不利位置的求解特点，本文在整体模型中对公路和轻轨疲劳荷载均采用影响线加载的方法找寻疲劳细节Ⅰ的最不利加载位置，并将对应的边界条件施加至空间板壳有限元模型中进行应力求解，其共有6 个工况，如下所示：

工况1：拉索处上横梁剪力最大；

工况2：拉索处上横梁剪力最小；

工况3：一般处上横梁2 剪力最大；

工况4：一般处上横梁2 剪力最小；

工况5：节点处上横梁剪力最大；

工况6：节点处上横梁剪力最小。

4 有限元模型

采用通用有限元软件ANSYS 建立该公轨两用斜拉桥钢桁梁3 个全幅桁架节段，纵桥向长度为3×15.1=45.3m。其中，模型考虑桥面系U 肋及板肋过焊孔、上弦杆与上横梁相交处过焊孔、上弦杆横隔板人孔及其加劲肋等构造细节，同时桥面板考虑2%横坡。

钢桁梁节段模型钢结构部分采用SHELL181 单元，材质为Q345 钢材，弹性模量为2.06×105MPa，密度为7.85×10-5N/mm3，泊松比为0.31。钢桁梁节段模型桥面铺装部分采用SOLID45 单元，材质为STC22，弹性模量为3.76×104MPa，密度为4.52×10-5N/mm3，泊松比为0.20。模型钢结构部分划分单元数7812531 个，桥面铺装部分划分单元数157035 个，其中，上横梁横隔板构造细节关注区域单元划分长度为20mm，一般位置关注区域单元划分长度为40mm，如图5 所示。

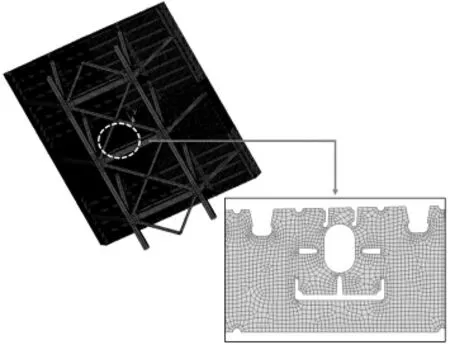
图5 钢桁梁节段有限元模型

节段模型边界采用位移边界，在各主要杆件的形心处建立形心节点，通过MPC184 单元耦合各杆端与对应的形心节点，然后在该节点上施加六个自由度的位移约束，约束值根据全桥整体模型对应加载工况提取得到。模型拉索处索力采用主节点刚性连接各拉索处沿纵桥向锚拉板范围内边上弦杆与顶板交界处的节点，再在主节点上施加对应工况下整体模型中的索力。由于该桥为公铁两用钢桁梁斜拉桥，模型下横梁处还需施加对应工况下轨道梁的支座反力。

5 计算结果及分析

针对一般位上横梁横隔板(包括一般位1 和一般位2)板厚的不同分为方案A 及方案B，其中方案A 的板厚为16mm，与表1 所示尺寸一致。方案B 的板厚为24mm，其余结构尺寸同表1。

基于上述疲劳计算方法及两个不同的方案，对拉索位、一般位2、节点位疲劳细节Ⅰ分别进行最大及最小剪力工况加载分析，记录各上横梁横隔板点位1 至点位41 的应力路径，方案A 结果如图6 至图9 所示，方案B结果如图10 至图13，点位位置如图3 所示。其中，节点平均结果记录应力幅变化趋势，节点非平均结果记录同一有限元节点处应力幅最大计算值。

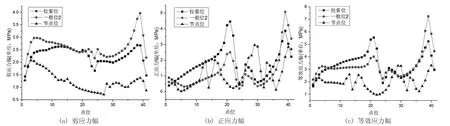
图6 上下层同时加载计算结果(节点平均)

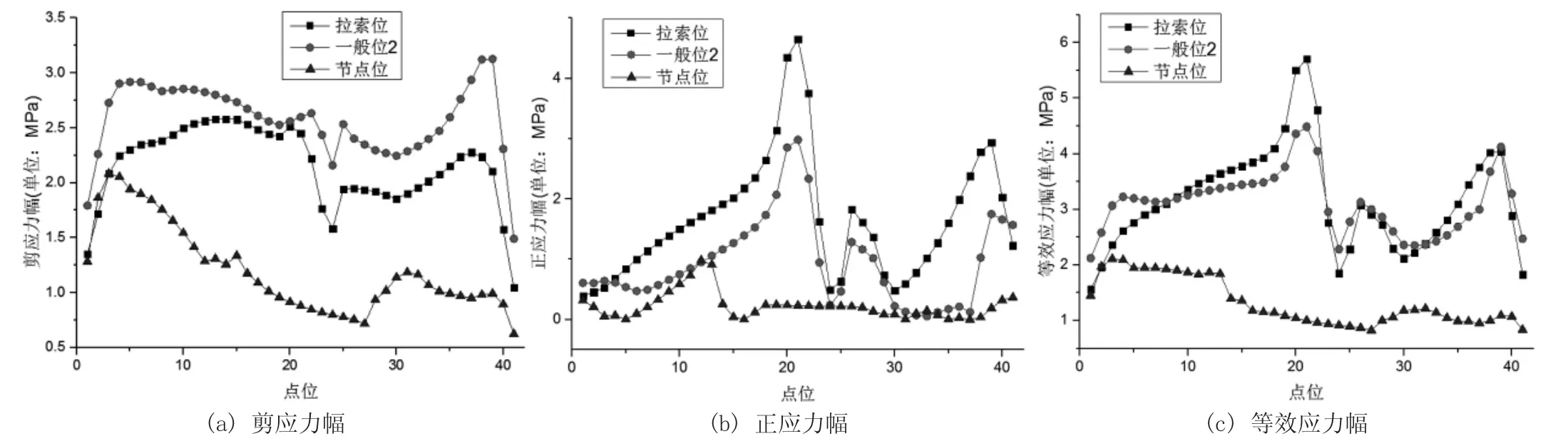
图7 上层加载计算结果(节点平均)

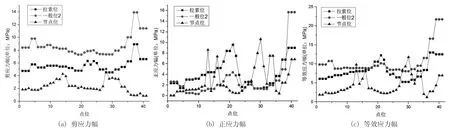
图8 上下层同时加载计算结果(节点非平均)

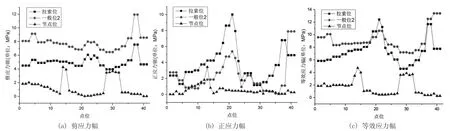
图9 上层加载计算结果(节点非平均)

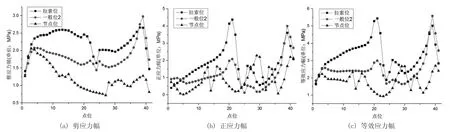
图10 上下层同时加载计算结果(节点平均)

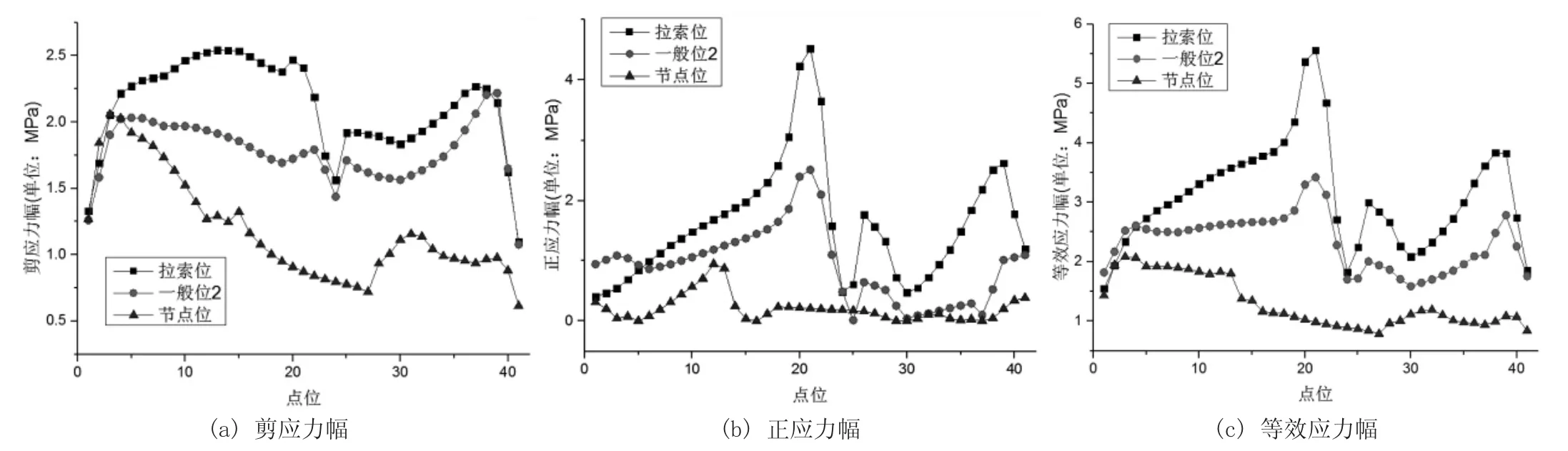
图11 上层加载计算结果(节点平均)

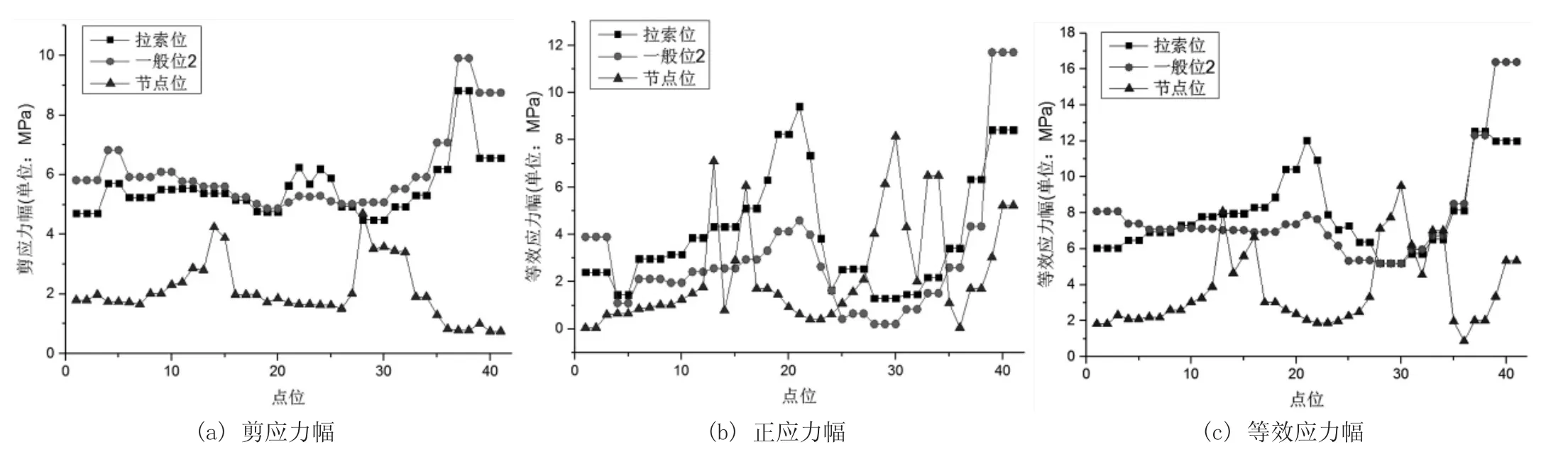
图12 上下层同时加载计算结果(节点非平均)

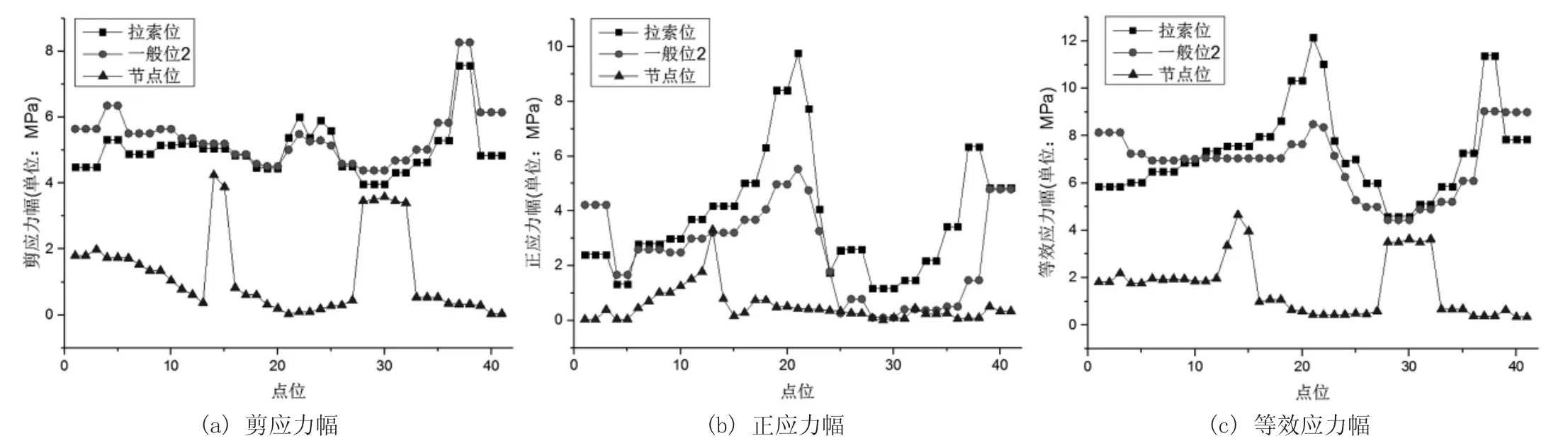
图13 上层加载计算结果(节点非平均)

5.1 方案A(一般位横隔板t=16mm)

由图6 可知，上下层同时加载时，拉索位与一般位2 处疲劳细节Ⅰ的剪应力幅、正应力幅及等效应力幅沿点位1 至点位41 路径的变化趋势类似，它们的应力幅突变区域均为上弦杆腹板加劲肋处及上弦杆下部靠近上横梁横隔板开孔处。节点位等效应力幅水平较拉索位与一般位2 处小，其应力幅突变区域为上弦杆腹板加劲肋处、上弦杆底板处及上层竖向节点板与上横梁下翼缘相交开孔处。上下层同时加载时，疲劳细节Ⅰ的节点平均等效应力幅峰值以一般位2 上弦杆下部靠近上横梁横隔板开孔处最大，数值为7.2MPa。

对比图6 和图7 可知，拉索位、一般位2 及节点位疲劳细节Ⅰ的剪应力幅均主要由公路荷载引起。拉索位、一般位2 上弦杆腹板加劲肋处的正应力幅主要由公路荷载引起，其上弦杆下部靠近上横梁横隔板开孔处正应力幅主要由轻轨荷载引起。节点位上弦杆底板处、上层竖向节点板与上横梁下翼缘相交开孔处的正应力幅主要由轻轨荷载引起。上层加载时疲劳细节Ⅰ的节点平均等效应力幅峰值以拉索位上弦杆腹板加劲肋处最大，数值为5.7MPa。

对比图6 和图8、图7 和图9 可知，节点平均应力幅沿点位1 至点位41 路径的变化趋势及峰值点位置与节点非平均应力幅类似，但节点非平均的结果均较节点平均大，其中，上下层加载时，拉索位、一般位2、节点位疲劳细节Ⅰ等效应力幅的节点非平均最大结果较节点平均最大结果依次大234%、300%、356%。上层加载时，其较节点平均最大结果依次大218%、299%、224%。

5.2 方案B(一般位横隔板t=24mm)

对比图10 与图6、图12 与图8 可知，当上下层同时加载时，方案B 疲劳细节Ⅰ各应力幅的突变区域与方案A 相比基本没变化。对于疲劳细节Ⅰ的剪应力幅，方案B 一般位2 处较方案A 有明显下降，而拉索位与节点位该处的剪应力幅均基本没有变化。对于疲劳细节Ⅰ的正应力幅，方案B 除拉索位处基本无变化外，一般位2与节点位处均有明显下降，因此上下层同时加载时，一般位2 及节点位疲劳细节Ⅰ的等效应力幅有明显下降，而拉索处基本不变。其中，一般位2 最大等效应力幅节点平均结果下降22.9%，节点非平均结果下降24.5%。节点处最大等效应力幅节点平均结果下降18.3%，节点非平均结果下降19.4%。

对比图11 与图7、图13 与图9 可知，当上层加载时，方案B 疲劳细节Ⅰ各应力幅的突变区域与方案A 相比基本不变。对于疲劳细节Ⅰ的剪应力幅及正应力幅，拉索位与节点位基本没变化，而一般位2 处有明显下降，因此上层加载时，一般位2 疲劳细节Ⅰ的等效应力幅有明显下降，而拉索位及节点位基本不变。其中，一般位2 最大等效应力幅节点平均结果下降23.8%，节点非平均结果下降32.6%。

5.3 疲劳分析结果

对方案A 及方案B 的等效应力幅按式⑷及式⑸进行计算得到疲劳细节Ⅰ的疲劳分析结果，其中式⑸左侧结果如表2 所示，式⑸右侧数值根据前述细节类别及相关参数，其数值为40.7MPa。

从表2 可知，方案A 疲劳细节Ⅰ最不利处为一般位上横梁横隔板2，其等效常值应力幅为47.0MPa，非平均结果不满足要求，此时富裕度为-15.5%。方案B 疲劳细节Ⅰ的最不利处与方案A 相同，其等效常值应力幅为35.5MPa，非平均结果满足要求，此时富裕度为12.8%。由上述结果可知，在拉索位、一般位2 及节点位上横梁横隔板中，加厚一般位横隔板板厚对一般位2 疲劳细节Ⅰ的抗疲劳性能改善最大，其次为节点位，而对拉索位基本无影响。

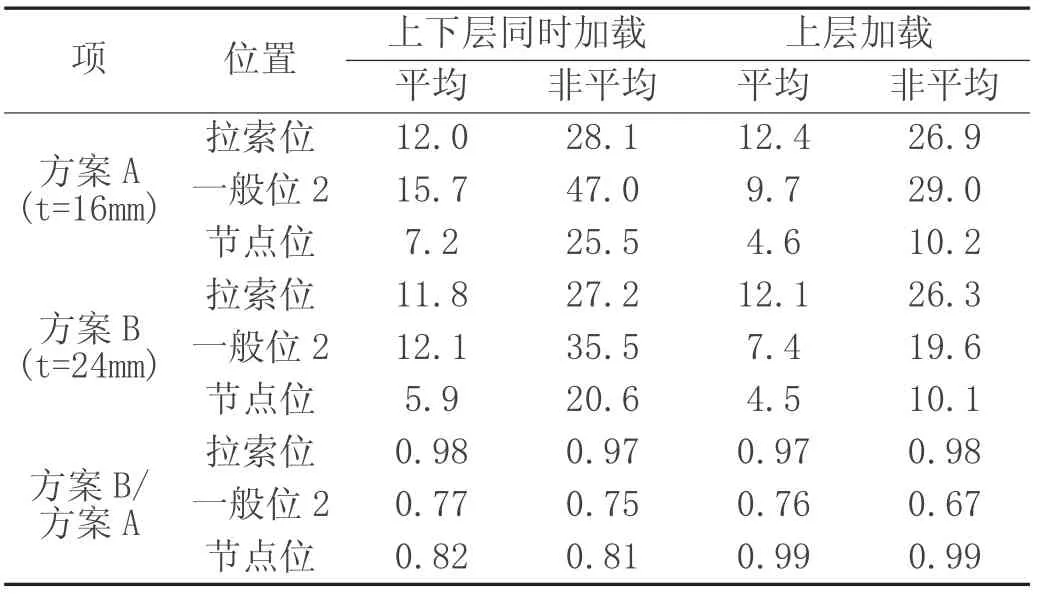
表2 疲劳细节Ⅰ等效常值应力幅(MPa)

6 结论

⑴在板桁组合桥面系拉索位、一般位2 及节点位上横梁横隔板中，上横梁与上弦杆相交处疲劳细节Ⅰ的最不利位置为一般位2 上弦杆下部靠近上横梁横隔板开孔处。同时，该处的剪应力幅主要由公路荷载引起，而正应力幅主要由轻轨荷载引起。上下层同时加载时，该处的正应力幅约为剪应力幅的1.3 至1.4 倍，下层轻轨疲劳荷载的影响不可忽略。

⑵在拉索位、一般位2 及节点位上横梁横隔板中，加厚一般位横隔板板厚对一般位2 疲劳细节Ⅰ的抗疲劳性能改善最大，其次为节点位，而对拉索位基本无影响。此时，一般位2 疲劳细节Ⅰ的最大等效应力幅降幅24.5%，疲劳性能改善效果较显著。