基于频域结构应力法的牵引电机结构振动疲劳分析

申政，方吉，汤黎明，杨敏，杨健，王耀亭

(1.中车株洲电机有限公司，湖南 株洲 412000；2.大连交通大学 机车车辆工程学院，辽宁 大连 116028)

随着我国高速列车的不断发展，牵引电机在动车组中的应用越来越广泛。由于列车速度的提升，为保证产品的可靠性，牵引电机焊接结构在高频振动条件下疲劳性能面临考验。关于结构的振动疲劳研究成为了热点问题，国内外专家、学者完成了一系列的研究。刘芬等[1]采用模态叠加瞬态响应分析法，获得该焊接结构中各节点的应力-时间，结合焊缝S-N曲线，Miner 线性累积损伤理论和雨流循环计数法，基于时域法估算母材及焊缝的随机振动疲劳寿命。朱颖等[2]基于改进区间分析和频域疲劳计算方法，对参数不确定结构在平稳高斯荷载作用下的疲劳损伤进行研究。关迪等[3]为研究随机振动条件下某型机载模块的疲劳特性，推导了功率谱密度下结构振动疲劳寿命的一般表达式，并利用高斯三区间法对其进行了简化分析。乔扬等[4]为研究高速飞行器受高频脉动噪声载荷激励下的结构声疲劳问题，讨论了基于应力谱的频域疲劳损伤计算方法，提出了一种基于统计能量理论(SEA)的结构高频随机振动疲劳寿命计算方法。肖渊海等[5]利用ANSYS Workbench有限元仿真平台，对无刷直流力矩电动机进行了轴向随机振动仿真分析。GHARAIBEH 等[6]利用Taguchi 方法研究了电子车辆在随机振动载荷作用下的疲劳寿命性能，给出了一种求解电子装配随机振动问题的解析解。WEI 等[7]提出了一般多轴随机载荷作用下的多轴疲劳寿命预测模型，并用al7075-T6 合金在不同随机单轴和多轴谱下的室内试验数据对所提出的模型进行了验证。OGRINEC 等[8]引入时域和频域(窄带和Tovo-Benasciutti方法)对单自由度动力系统在完全分离的半正弦脉冲激励下的时域和频域损伤的理论进行了相关研究。MIRONOV 等[9]基于薄试样试验提出了完整应力-应变图的方法，该方法可以基于实验运动曲线与载荷矢量的交集用作疲劳失效的判据。WOLFSTEINER等[10]分析了一般多共振频率振动系统的局限性，提出了基于高阶谱的改进方法。牵引电机壳体主要采用焊接的方式获得，而焊接结构的疲劳寿命主要取决于焊缝的疲劳寿命，另外，电机壳体结构主要承受振动载荷作用，因此要做到电机壳体结构的疲劳寿命可靠预测，需要有能够可靠预测焊缝的疲劳寿命的方法，同时能够将结构的振动对焊缝疲劳寿命的影响考虑进去的新方法。方吉等[11-12]基于网格不敏感结构应力法提出了频域结构应力法，该方法是否可以服务于电机结构的疲劳寿命评估，本文进行了相关计算与试验对比分析。

1 频域结构应力法及试验验证

车辆结构在线路运行条件下所承受的动载荷主要源自于轨道激励的作用，主要包括轨道不平顺、轮对及钢轨的制造误差、轨道接缝、轮对和轨道不均匀磨损、地基的刚度不均匀等随机激励都会引起轨道车辆结构的随机振动。

为了将网格不敏感结构应力引入到频域实现焊接结构随机振动疲劳寿命预测，方吉等[13]将随机振动的理论与网格不敏感结构应力法相结合，首先基于随机振动基本理论，线性系统的响应可以由式(1)获得：

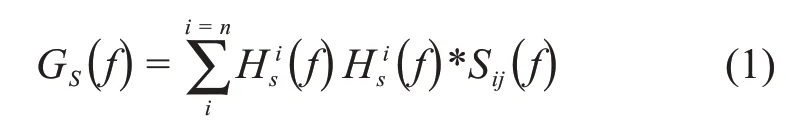
其中：Sij(f)是输入载荷的自功率谱或互功率谱；为系统的位移传递函数；为其共轭。将式(1)中的位移传递函数经过线性转换可获得焊趾处各节点等效结构应力Ss(f)的传递函数：

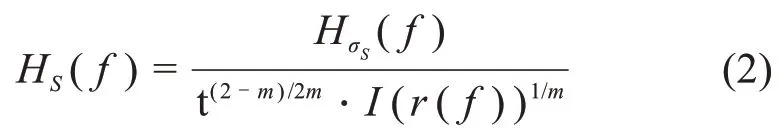
式中：I(r(f))是频域下的弯曲比函数；m为常数[14]。其中HS(f)是根据位移响应函数计算获得的结构应力响应函数。因此HS(f)可称之为等效结构应力的频率响应函数。

然后，基于Dirlik 法统计获得等效结构应力概率密度函数P(S)，根据Miner 疲劳损伤积累原理及主S-N曲线，就可以计算焊缝焊趾处节点的疲劳损伤。基于该思路作者提出了频域结构应力法。基于频域结构应力法的焊接结构随机振动疲劳寿命预测具体的流程见图1。

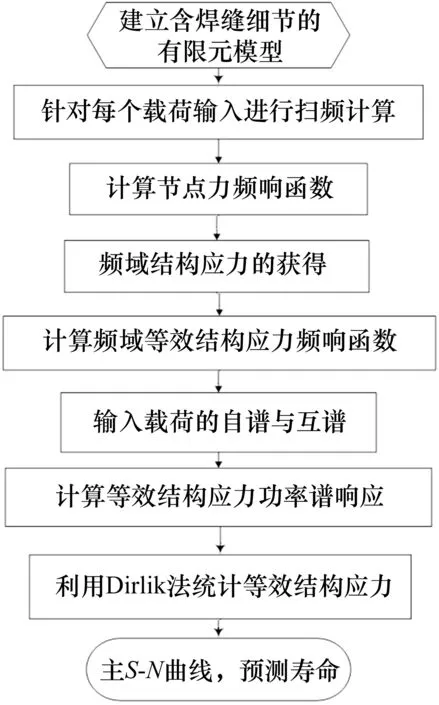
图1 基于频域结构应力法的疲劳寿命预测流程Fig.1 Fatigue life prediction process based on frequency-domain structural stress method

当外载荷激励频率与结构的模态频率存在交集的情况下，结构阻尼参数的设置对结构的振动响应影响较大。结构阻尼系数主要取决于结构材料的内摩擦，取值范围一般为0.1～0.15 之间。为了验证牵引电机结构电机壳体常用材料Q345E 钢的结构阻尼选值的合理性，特设计了如图2所示的随机振动疲劳试件。主要包括质量块、支板、底板3部分，其中质量块与支板，支板与底板通过全焊透角焊缝连接，并且通过探伤确保为全焊透。

图2 焊接结构试件Fig.2 Welded structure sample

采用航天希尔MPA403/M124 小型振动台，进行疲劳试验(如图3 所示)。试件载荷采用IEC 61373：2010 版中的2 类载荷谱，将其模拟长寿命垂向加速度载荷谱转换成时域载荷进行疲劳试验。加速度激振方向与试件板面方向垂直如图4所示。

图3 MPA403/M124 小型振动台Fig.3 MPA403/M124 test rig

图4 加速度激振方向Fig.4 Acceleration direction of excitation

通过试验可以观察到裂纹从焊缝中部开始扩展到一定阶段后(见图5)，会迅速发生断裂，寿命以裂纹扩展阶段为主，失稳断裂所占的时间非常短，可以以试件的断裂作为试验寿命的终止。由于疲劳试验的结果具有一定的离散性，本次试验一共进行了8个试件的随机振动疲劳试验，试验结果如图6所示。根据试验结果可以得出，50%存活率下，试验所得的寿命为17.8 min。

图5 试件疲劳开裂位置Fig.5 Fatigue crack location of sample

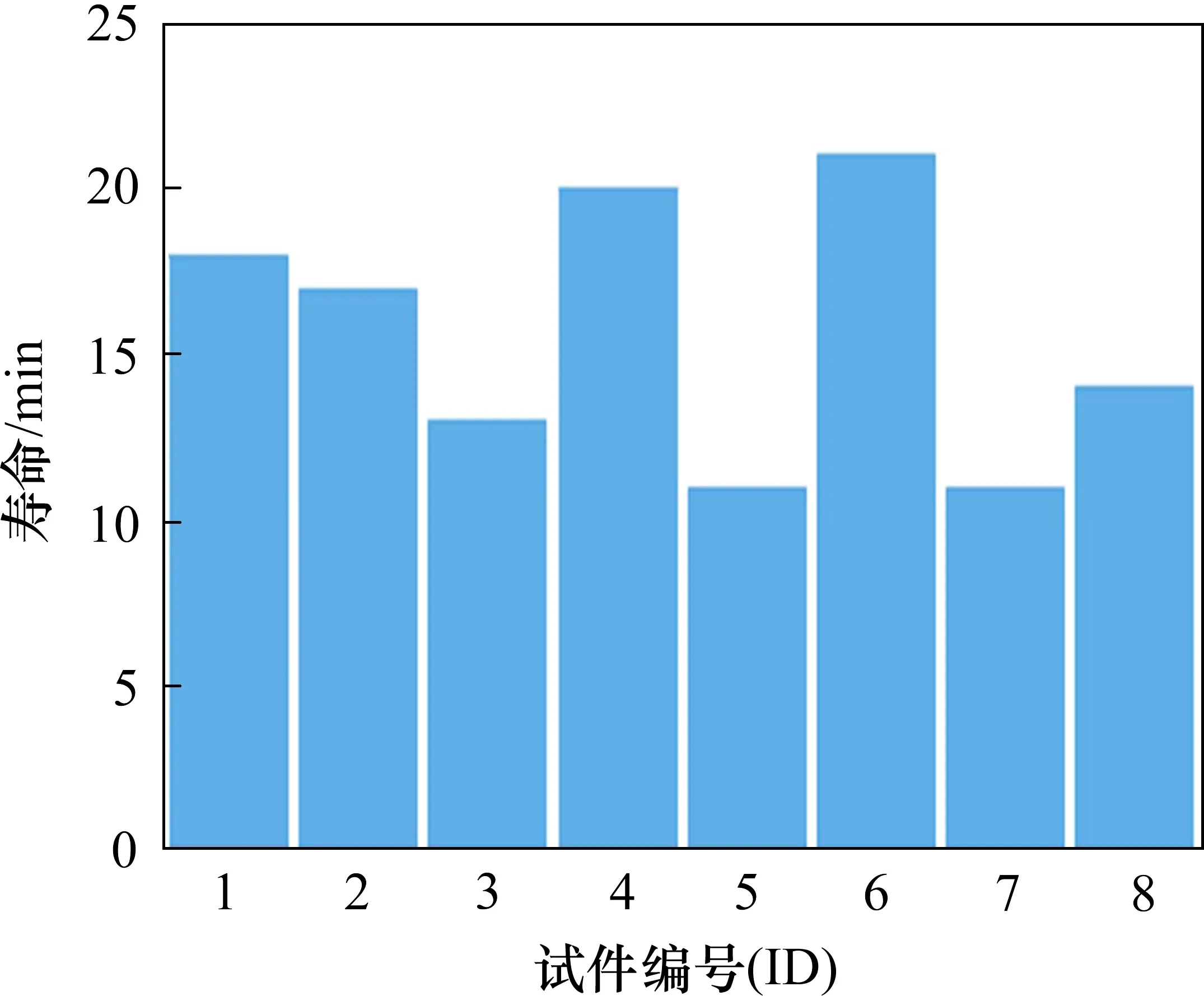
图6 试件疲劳寿命分布Fig.6 Fatigue life distribution of samples

根据试件几何尺寸建立对应的有限元模型，单元划分时主要采用六面体结构网格，节点数34 632，单元数28 957。实际试样由于焊缝收缩，靠近底板处，支板板厚收缩至7 mm，因此在靠近焊趾位置处，板厚建模为7 mm。总体有限元模型及焊趾局部如图7所示。

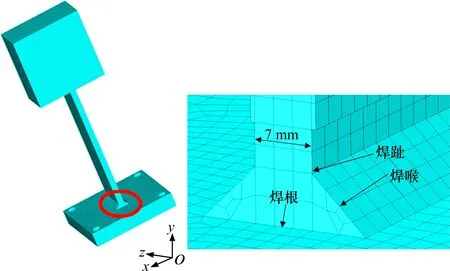
图7 试件有限元模型及局部放大图Fig.7 FE model and partial enlarged drawing of sample

材料参数按照Q345E 钢的参数进行设置，杨氏模量E为206 GPa，密度ρ为7.8 g/cm3，首先进行模态计算，模态计算的位移约束边界条件保持试验一致，即底板下表面施加固定约束，采用Lanczos 法计算部分低频模态，200 Hz 以内的模态有3阶如表1所示。

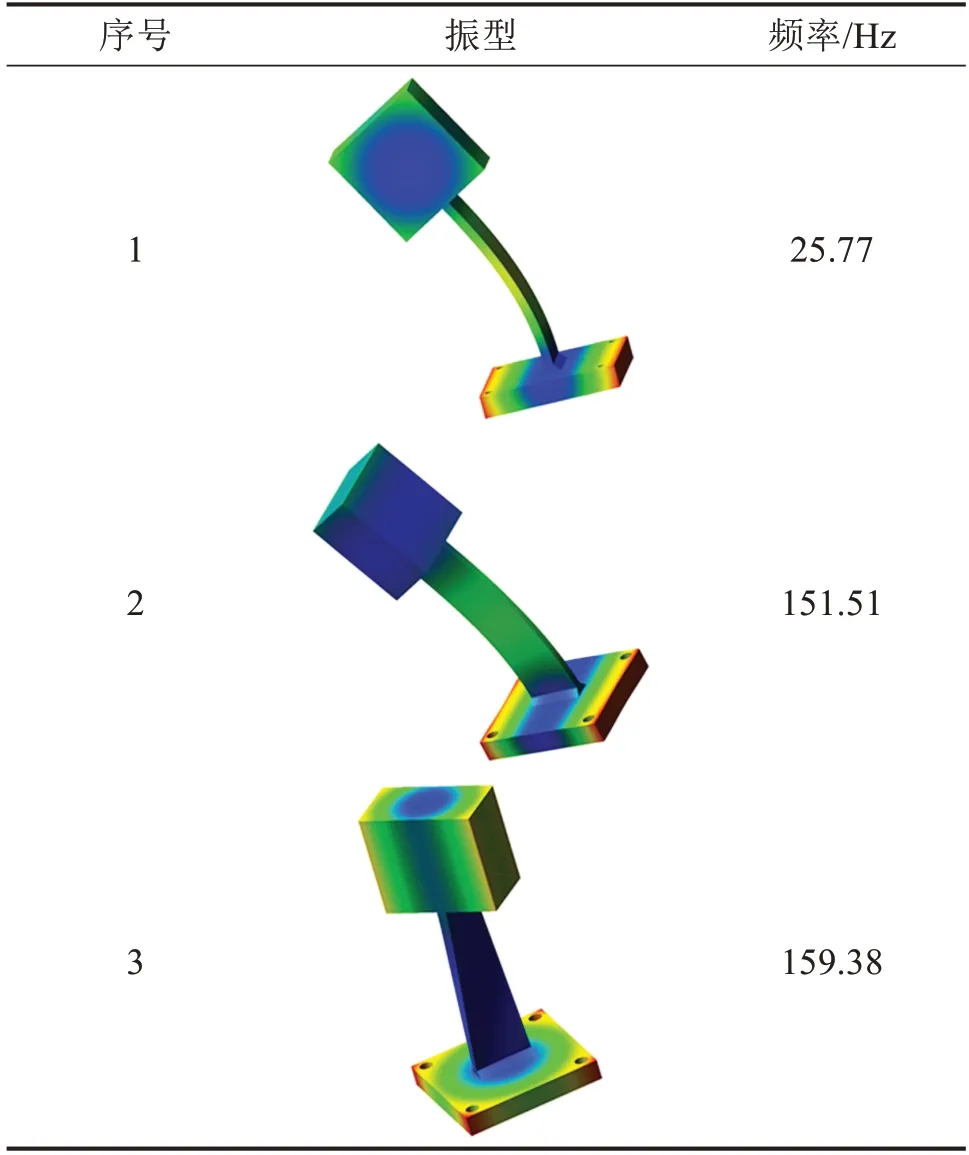
表1 试件模态结果Table 1 Calculated mode of sample

采用大质量法进行垂向谐响应计算，频率间隔1 Hz，计算频率范围为5～250 Hz，结构阻尼系数D=0.02，基于位移响应结果计算对应的频域结构应力。

仿真计算施加的载荷谱与试验保持一致，采用频域结构应力法计算可以获得焊线焊趾处所有节点的等效结构应力功率谱，26 Hz 处的等效结构应力功率谱分布如图8 所示，焊缝危险点(见图11)的等效结构应力功率谱如图9所示。

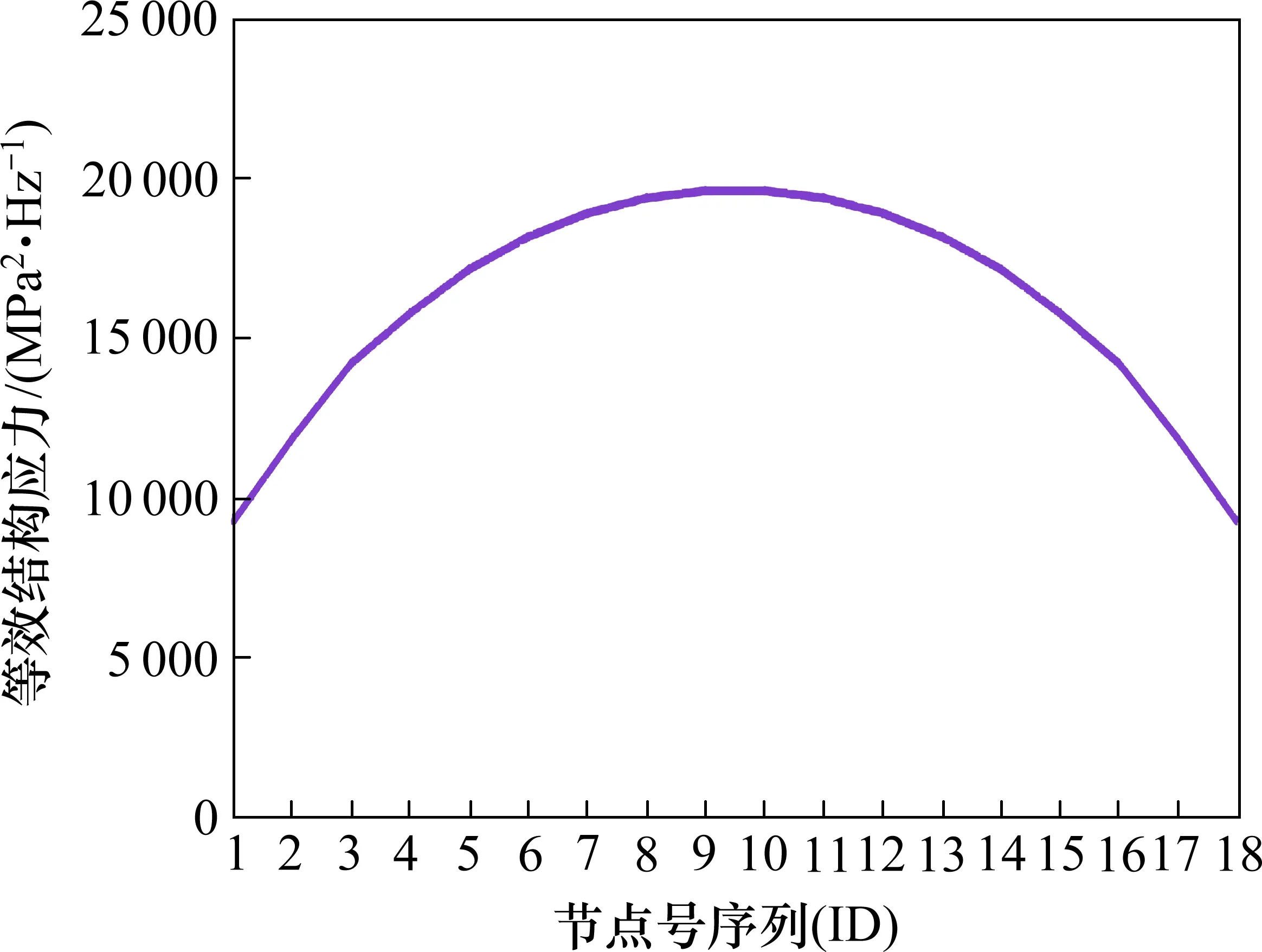
图8 沿焊缝等效结构应力功率谱幅值分布(26 Hz)Fig.8 Power spectrum amplitude distribution of equivalent structural stress along weld line(26 Hz)

图9 疲劳危险点等效结构应力功率谱分布图Fig.9 Equivalent structure stress power spectrum distribution of fatigue weak point

结合主S-N曲线，通过计算获得了如图10 所示的疲劳寿命结果，其最大损伤发生在中部区域，寿命时间为9.97×102s，折合16.6 min，该计算结果与50%存活率下，试验所得的寿命17.8 min 很接近，且疲劳开裂的起始位置也与试验基本一致。

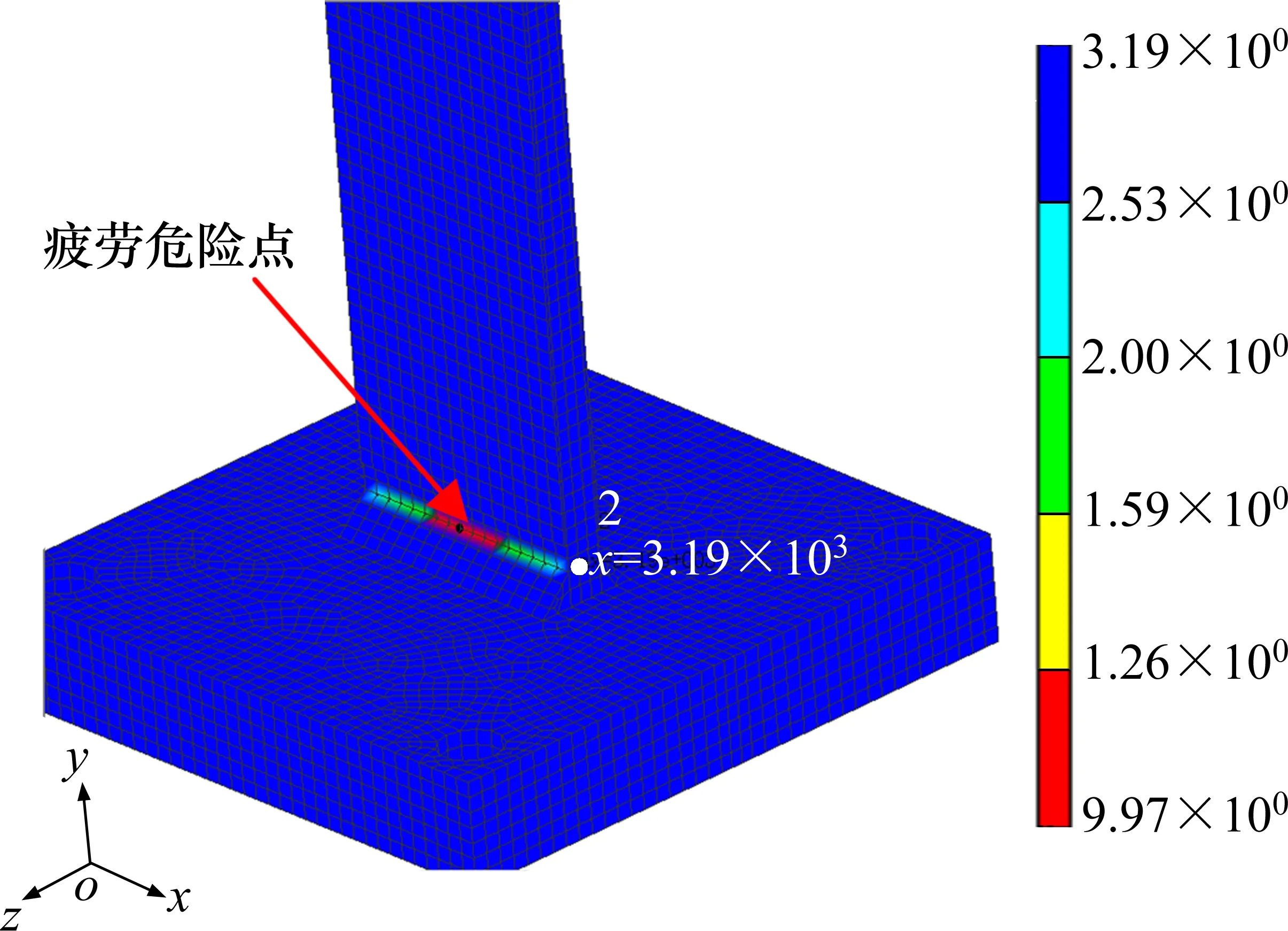
图10 焊线疲劳寿命分布Fig.10 Fatigue life distribution of welding line

2 带焊缝细节的电机有限元模型的建立

2.1 电机有限元模型的建立

本次计算采用6 面体和5 面实体单元对电机壳体进行离散，单元总数为69 855，节点数为99 817。电机总质量为625 kg，其中转子采用实体单元模拟，通过弹簧单元将转子固定在前后端盖上(如图11 所示)。为了方便在Ansys 软件中施加基础振动加速度载荷，采用大质量法，阻尼系数D=0.02，进行谐响应计算。由于接触单元始属于非线性连接不能用于模态和频域计算，因此端盖与模型壳体之间采用螺栓实体单元链接，接触面处没有施加绑定粘接接触，压圈与铁芯之间接触面没有定义接触连接(因此连接刚度比实际弱一些，计算评估结果偏保守一些)。

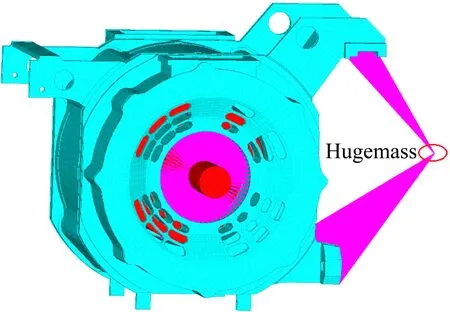
图11 电机有限元模型Fig.11 Finite element model of motor structure

2.2 关键焊缝的定义

焊接结构与金属结构疲劳现象不同，焊接接头的疲劳失效模式是可以提前预知的。XING 等[15]基于大量的工程实例，指出了焊接接头典型疲劳破坏形式主要有以下2种：一种是板破坏，称为模式A，起始点可能在焊趾或焊根处，依赖于焊接接头的具体形状；另一种是焊缝破坏，称为模式B，它穿透焊缝而破坏。模式B的破坏可以通过设计适当的焊缝尺寸和使用适当的焊接工艺予以避免。通常情况下，焊脚的尺寸大于板厚的焊缝绝大部分是疲劳破坏模式A。针对电机壳体结构的受力特点，选取了如图12中的12条关键焊缝。

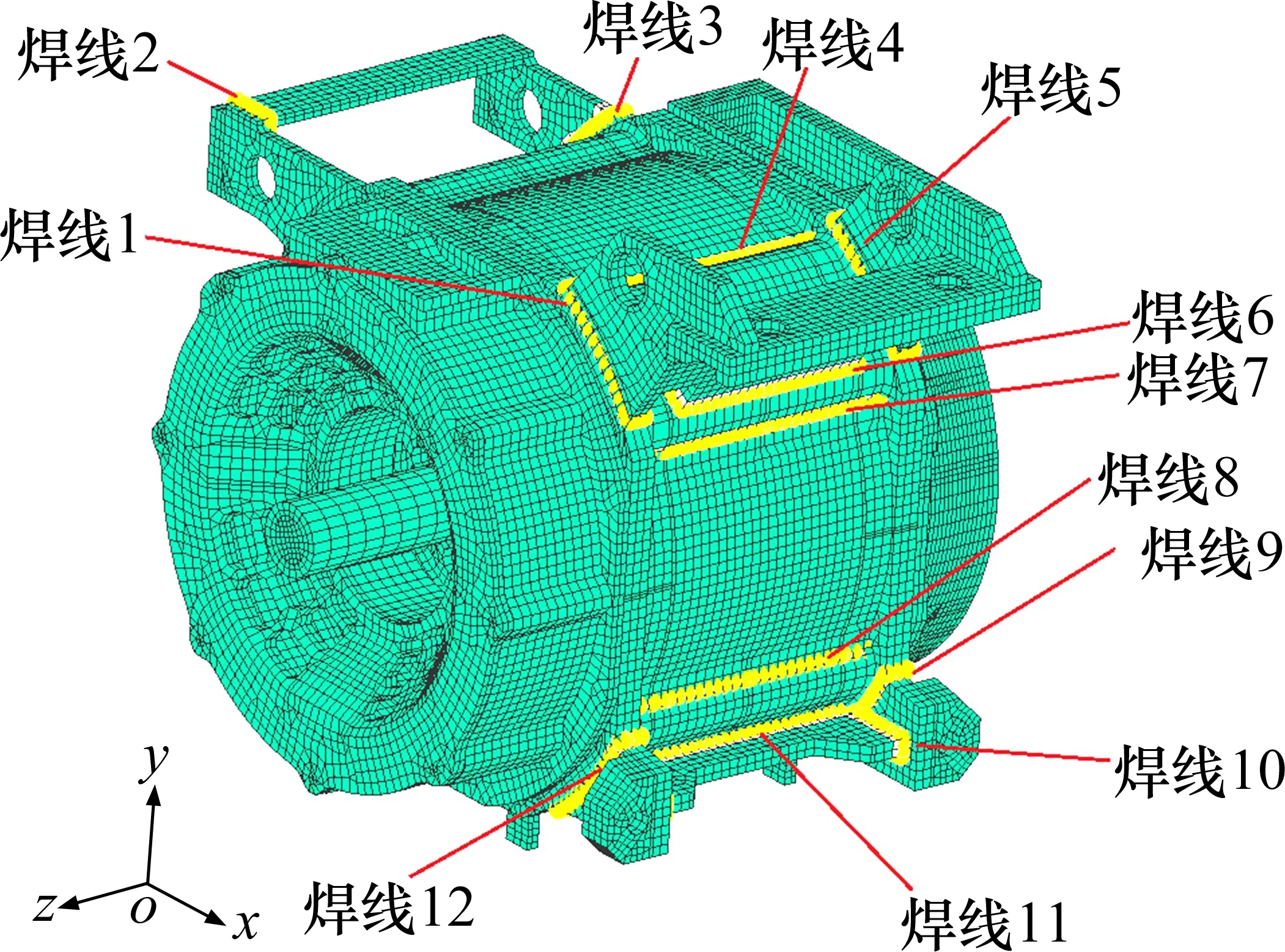
图12 焊线的定义Fig.12 Definition of weld line

3 电机壳体结构模态及频率响应分析

在电机与转向架连接处的刚性单元上施加6自由度的固定约束，采用Lanczos 法计算约束模态，前5 阶模态频率如表2 所示。通过电机的模态计算结果可以看出电机壳体结构的最低阶模态频率高于IEC 标准中2类对应的载荷频率范围，因此不存在交集，结构的共振可能性很小。

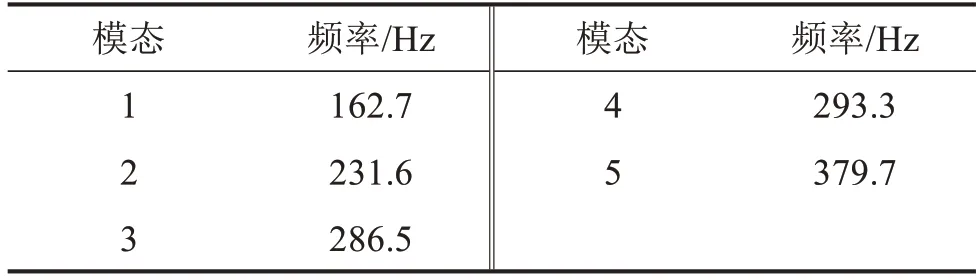
表2 电机结构约束模态Table 2 Constrained mode of motor structure

4 关键焊缝的随机振动疲劳分析

4.1 载荷的施加

基于IEC 61373：2010 标准中的2 类，转向架构架安装的，模拟长寿命随机振动加速度载荷谱，根据电机结构的质量选取频率范围为2～100 Hz，其中垂向、横向、纵向3 个方向的功率谱如表3所示。

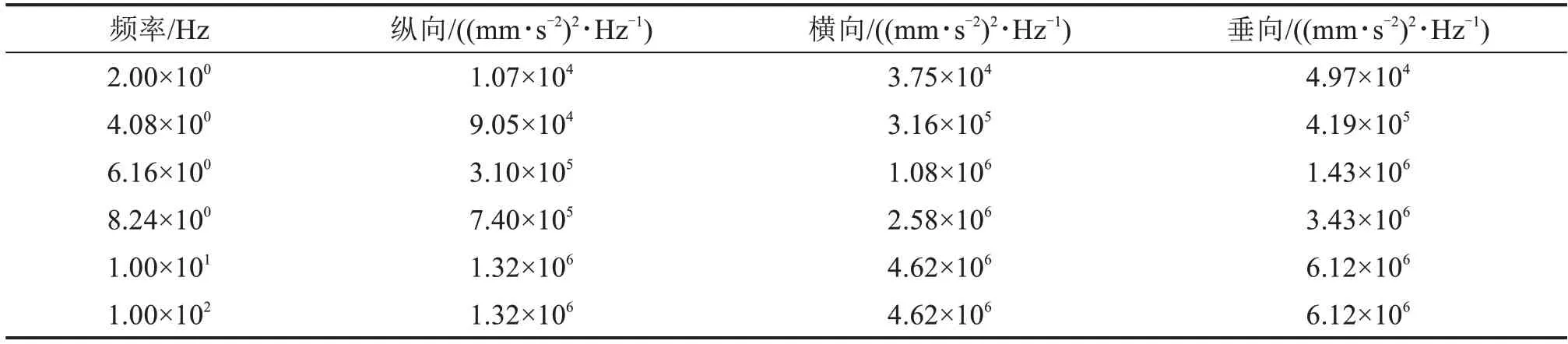
表3 施加的随机加速度谱Table 3 Applied random acceleration spectrum

4.2 主S-N曲线的选取

为了方便计算寿命与试验寿命进行对比，采用钢材料的中值主S-N曲线(如图13 所示)，进行疲劳寿命评估。

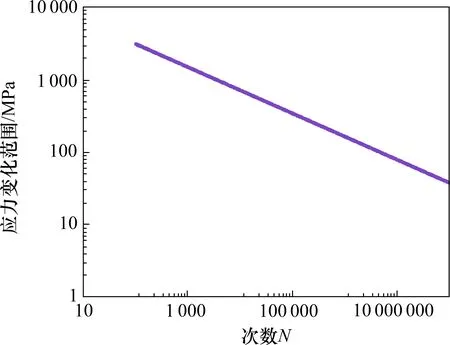
图13 钢材料的中值主S-N曲线Fig.13 Mean master S-N curve of steel material

4.3 疲劳寿命预测

基于IEC 61373：2010 标准，模拟长寿命随机振动疲劳试验要求，考察结构分别在纵向、横向、垂3 个方向，每个方向5 h，总共15 h 随机激振载荷下结构的疲劳总损伤。首先计算单个方向随机载荷作用下单位时间(s)内的损伤，然后利用MINER线性损伤累积法计算总损伤：

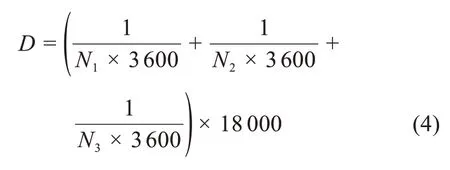
式(4)中：N1，N2，N3分别为垂向、横向和纵向随机载荷单独作用下结构的疲劳寿命(单位：h)；D为3 个方向各5 h 的累积总损伤，随后基于IEC 61373—2010 标准针对该电机结构进行了模拟长寿寿命随机振动疲劳试验。经过3 个方向每个方向5 h，总共15 h 的激振过后，经检测该电机壳体结构无裂纹产生，模拟长寿命随机振动疲劳试验一次性通过，证明该电机结构抗疲劳性能满足设计要求。

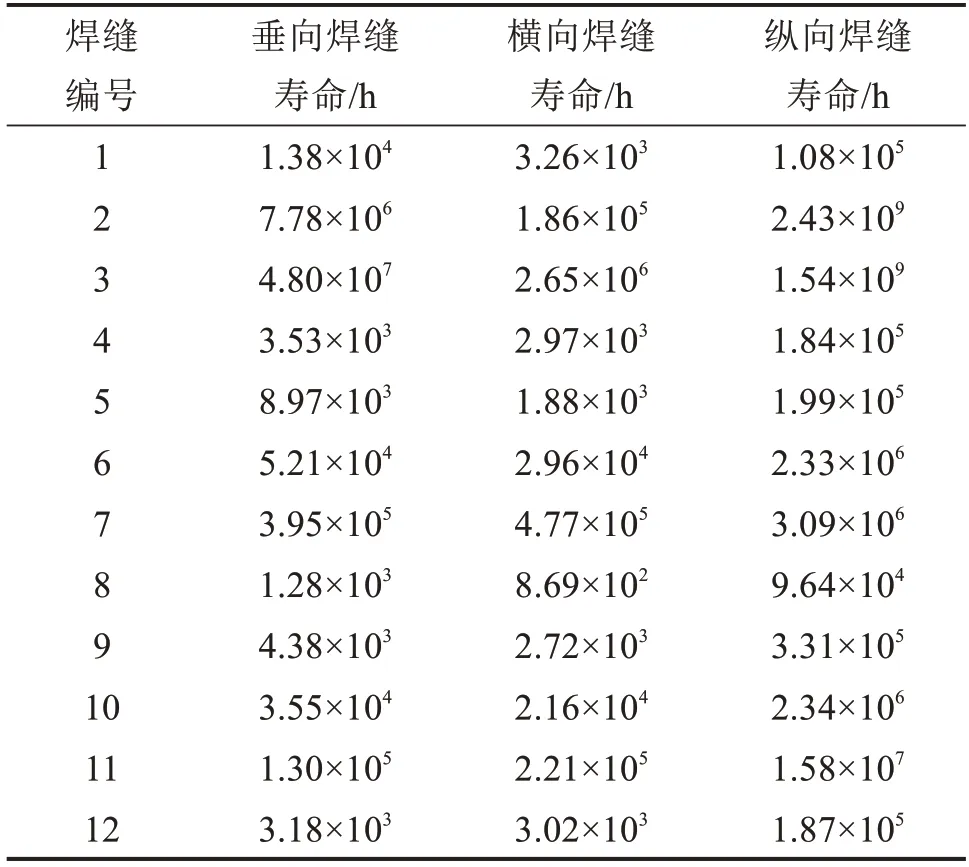
表4 电机结构关键焊缝随机振动疲劳寿命评估结果Table 4 Random vibration fatigue life prediction results of key welds in motor structure

5 结论

1) 通过焊接试件的随机振动疲劳试验，验证了频域结构应力法可以考虑模态振动对焊缝疲劳寿命的影响，其评估结果准确有效。

2) 通过电机的模态分析可以看出电机壳体结构的最低阶模态频率高于IEC 61373：2010 标准中2 类对应的载荷频率范围，不存在交集，结构的共振可能性较小。

3) 电机的随机振动疲劳寿命分析结果显示，该电机的壳体焊缝疲劳寿命远高于IEC 61373：2010 标准要求的15 h，说明该电机结构抗疲劳能力满足设计要求。

4) 该电机结构的随机振动疲劳试验过程中未出现焊缝疲劳失效现象，试验结果与分析评估结果一致，说明频域结构应力法可以为电机焊接结构的抗疲劳设计提供有效的技术支持。