考虑潮汐荷载作用的沉管隧道竖向位移计算

周桓竹，王延宁,2，寇晓强

(1.汕头大学 土木与环境工程系 广东省结构安全与监测工程技术中心，广东 汕头 515063；2.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221000；3.清华大学 土木水利学院，北京 100084)

沉管隧道是一种越洋跨海的海底隧道，无论是在造价上还是技术上都具有诸多优点。当下沉管隧道建造在跨越繁忙水运航道的发达地区，多属于深埋隧道，河床上覆回淤土层透水性较弱，常年受潮汐荷载影响，当潮位变化速度大于回淤土层透水速度[1]时，可将某时刻作用于河床的潮汐荷载等效为该时刻潮位变化产生的水压差，管节由此随着潮汐水位的升降发生相应的周期往复运动[2]。谢雄耀等[3]发现柔性沉管隧道变形受到多种外部荷载的共同作用，其中，潮汐荷载影响下的变形所占比重较大，占运营期总沉降的4%～10%。因此沉管管节在竖向位移的影响下，极其容易发生疲劳损伤，尤其是接头部位对沉降表现更为敏感。在以往的研究中，对于潮汐荷载在沉管隧道竖向位移产生的影响中理论分析偏少[4]。邵俊江等[1,5]分析了循环荷载下地基的固结变形，忽视了沉管自身的变形。HU 等[6-7]通过实验提出了潮汐荷载下的沉管隧道变形分析方法，谢立广等[8]用组合弹簧模拟管节接头，禹海涛等[9]建立沉管接头压缩力学模型，却没有相对应的变形计算方法。以上学者将地基变形和节段变形分开讨论，忽视了地基和管节之间的差异沉降。ZHOU 等[10]建立了黏弹性地基上的Euler 梁模型，然而没有考虑管段剪切变形。虽然后期陆世杰等[11]研究了Timoshenko 梁模型，但是在挠度分析时，将地基压缩基床参数视为常数，存在不足。综上所述，同时引入地基变形和管节接头受力，将地基压缩基床参数视为伴随时间变化的变量，考虑管节的抗弯和抗剪，将沉管隧道等效为置于Winkler地基上的Timoshenko梁，以此推导其竖向变形计算公式。进一步以甬江沉管隧道工程为例，分析沉管隧道在潮汐荷载下伴随时间变化的管节竖向位移，并与Euler 梁模型相对比，分析区别。

1 方法与假定

1.1 基本假定

潮汐荷载下沉管隧道竖向位移的求解是一种复杂的相互作用系统，通常采用两阶段法进行计算：首先推导出潮汐荷载引起的土层非线性固结沉降[11]，反算得到不同时刻的等效压缩基床参数；然后考虑接头受力，建立管节-接头计算模型。

为了保持该方法的理论严谨性，给出如下假设：

1) 将潮汐荷载等效为正弦波形循环函数，不考虑其他荷载引起的土层位移；

2) 将管节简化为水平布置，假定土层沿管节纵向均匀分布。

1.2 计算潮汐荷载

多位学者采用三角函数来刻画潮汐荷载随时间的变化，以潮位最低点为基准，tk时刻下的潮汐荷载q(tk)可以表达为：

式中：q0为平均潮位与潮位最低点间的水压差；q1，q2，ω1和ω2分别为潮位日变化和季节性变化引起的荷载幅值和变化角频率。进一步引入时间变量，便可以计算出任一时刻下的潮汐荷载。

1.3 计算土层沉降

自Gray 首先给出双层地基固结解答以来，已有不少学者致力于2层以上地基固结理论研究，本文基于谢康和等[12]提出的半解析法计算土层非线性固结沉降，给出tk时刻地表沉降Sk的表达式：

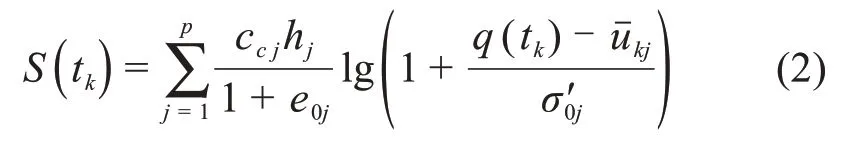
式中：cc j为土层j的压缩指数；hj为土层j的厚度；e0j为土层j的初始孔隙比；q(tk)为tk时刻的潮汐荷载；为土层j在tk-1时段最终时刻的平均超静孔压；为土层j的初始平均有效应力。

1.4 等效压缩基床参数

将基床压缩参数等效为伴随固结进程和外荷载变化的变量，通过提取任一时刻下的潮汐荷载和土层沉降反算得到。在保证潮汐荷载拟合度的情况下，可以得到相对精确的等效压缩基床参数，计算公式为：

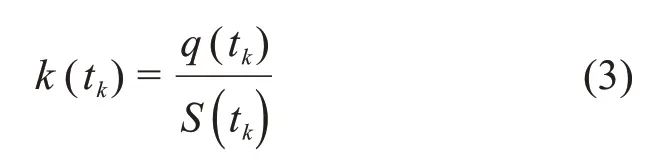
等效压缩基床参数的取值由下卧土层固结沉降和潮汐荷载二者共同确定。谢康和等[12]提出的变荷载下成层地基非线性固结沉降的半解析法具有较高的可靠性，不再赘述。

2 管—土相互作用模型

2.1 Timoshenko梁模型微分方程的建立

在现有沉管隧道的结构受力及变形研究中,大多将管节简化为Euler 梁模型，忽略了管节间的剪切变形。现将沉管隧道认作是在Winkler 弹性地基上的具有恒定截面的Timoshenko梁，如图1。考虑管节横向宽度B，将某时刻下的潮汐荷载P(tk)施加到现有沉管隧道。沉管隧道系统总势能Ω 计算表达式为(4)：

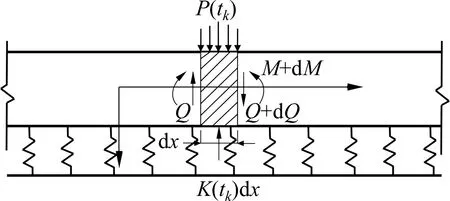
图1 Winkler地基上的Timoshenko梁模型Fig.1 Timoshenko beam model on Winkler foundation

式 中：K(tk)=B·k(tk)，P(tk)=q(tk)·B，EI，GA分别为沉管隧道的抗弯刚度和抗剪刚度；s，φ，ds/dx-φ分别为沉管隧道的挠度，弯转角和剪切角；fs为考虑沉管隧道截面剪应力非均匀分布的系数。

在计算中，沉管隧道系统总势能是恒定不变的，对其进行分部积分得到表达式(5)：

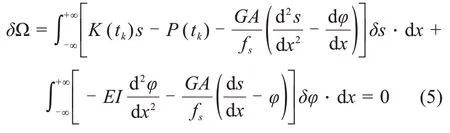
整理之后可得到表达式(6)～(7)：

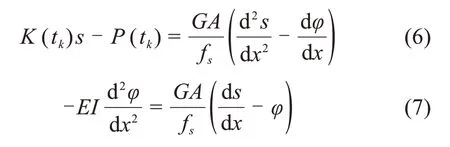
结合式(6)～(7)，得到Timoshenko 梁模型下沉管隧道的挠度变形微分方程为式(8)：

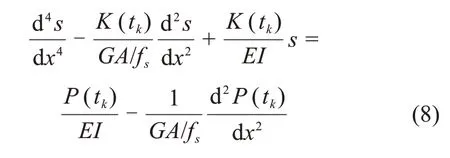
可以观察到上式中存在关于抗剪刚度GA的项，如果去掉此类，则可简化为基于Winkler 地基Euler 梁模型的沉管隧道的挠度变形微分方程，此处不再赘述。有关此模型的沉管隧道挠度探讨见魏纲等[13]的研究。

根据挠度和转角的关系可得式(9)：

进一步得到Timoshenko 梁模型下沉管隧道的弯矩[14]为式(10)：

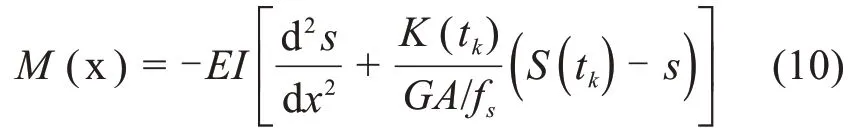
根据弯矩和剪力之间的关系[14]可以得到Timoshenko梁模型下沉管隧道的剪力为：

计算中，挠度s，转角θ，弯矩M(x)，剪力Q(x)均以使沉管发生顺时针转动方向为正[12]。

2.2 Timoshenko梁模型微分方程的解析

P(tk)=0 时，Timoshenko 梁模型下沉管隧道的挠度变形微分方程对应的特征方程表达式为：

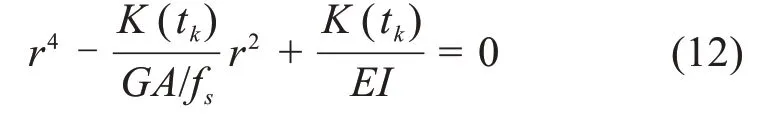
进一步得到沉管隧道挠度变形方程为：

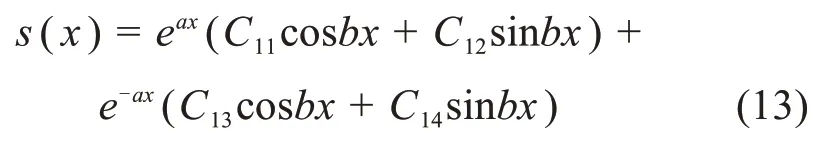
其中：C11,C12,C13,C14为代求数值，此时引入边界条件，当x=0时的挠度s0，转角θ0，弯矩M0和剪力Q0。用前4 个的数值表示后4 个的数值，表达式如(14)～(17)。

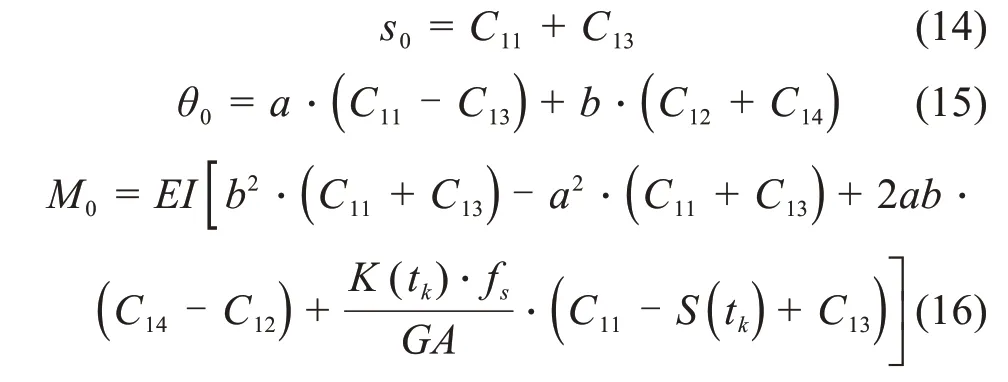
为方便简化计算，另外引入以下5 个表达式(18)～(22)：

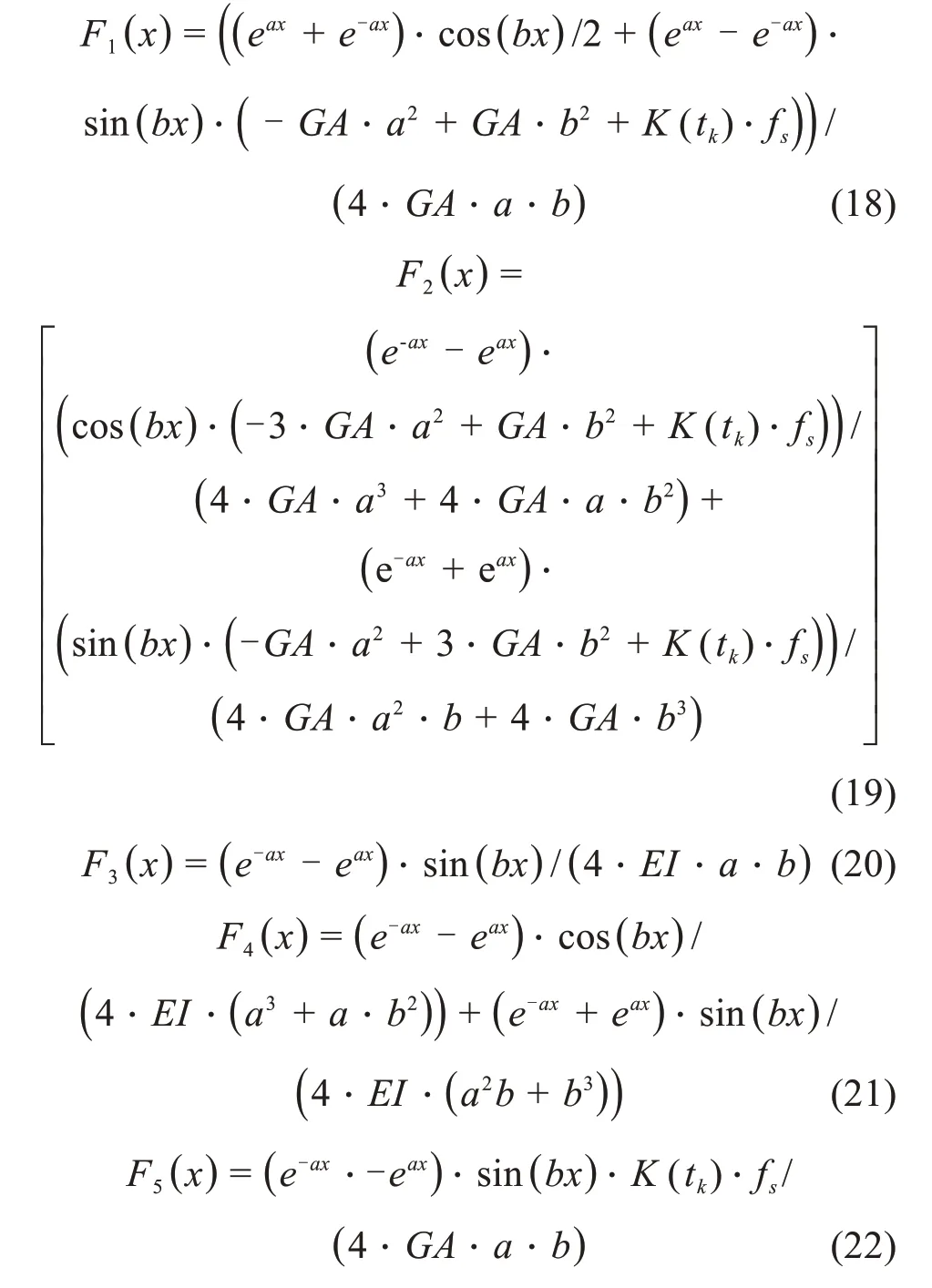
对于沉管隧道变形计算，继续引入管节所受到的潮汐荷载和接头力，考虑管节实际受力方向，得到Winkler 地基上Timoshenko 模型下的管节任一截面的挠度表达式为式(23)：

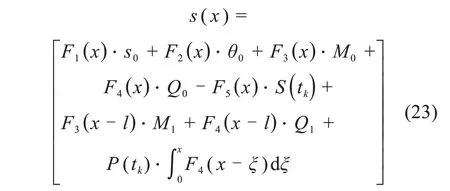
其中，

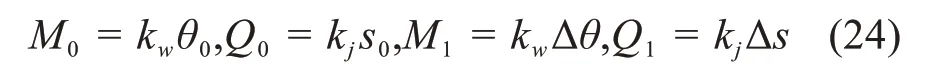
式中：M1,Q1分别为相邻管节处的弯矩和剪力；Δθ,Δs分别为相邻管节端面转角差和竖向位移差；kw,kj分别为接头抗弯刚度和抗剪刚度。本文选取离散时间段下的潮汐荷载，在土层沉降计算中对管节-接头模型逐级加载，通过数值迭代，进行MATLAB 编程，求解潮汐荷载沉管管节竖向位移。

3 算例

3.1 工程参数

越洋跨海的沉管隧道受潮汐荷载影响变形明显，然而近年来缺少这类沉管结构的实测数据，现以甬江沉管隧道为例，进行实测数据和理论沉降的对比分析。甬江沉管隧道修建于宁波甬江下游段，隧道长度为1 019.97 m，沉管段总长为420 m，沉管共由5 段管节组成，自北向南依次记为E1～E5(85 m+80 m+85 m×3)，如图2。通过查阅胡安峰等[15]有关研究，甬江沉管隧道下卧土层自上而下取值依次为0.5 m 的粉质黏土层、6 m 的淤泥质黏土层和4.5 m的淤泥层。其他参数见表1。

甬江沉管隧道使用C50混凝土，因此，在对管节进行计算时，取管节重度γ=25 kN/m3，弹性模量E=3.45× 104MPa。接头由橡胶材料制作，在工作水压区间变化范围内，根据接头与管体的弯曲刚度比和剪切刚度比[15]，取接头抗弯刚度kw=3.2 × 106(kN·m)/rad，抗剪刚度kj=1.1×106kN/m。目前的研究暂时不涉及由于管节自重、车辆荷载和河床淤积、清淤等引起的管节沉降。为了方便与实测数据进行对比，现移动低平潮下的计算沉降曲线至16 mm 实测初始沉降位置处，同时，高平潮下的计算沉降曲线随之移动。通过三角函数拟合[1]得到潮汐荷载参数：

下面以隧道J2 接头为例，基于Timoshenko 梁模型和Euler 梁模型讨论沉管管节接头竖向沉降差异。

3.2 分析比较

对于Euler 梁模型而言，通过MATLAB 拟合，可以得到J2接头截面竖向位移图，如图3(a)。结合众多学者的研究，对比J2 接头高平潮和低平潮下的计算沉降与实测沉降，从图4(a)中可以发现，前期管节的计算沉降大于实测沉降，中后期管节的计算沉降小于实测沉降，拟合的不是很准确。基于此，本文进一步在Euler 梁模型上改进，引入管节接头的剪切变形，建立Timoshenko 梁模型，通过数值模拟可以得到J2 接头截面竖向位移图如图3(b)，与实测沉降的对比如图4(b)，可以发现，除后期的计算沉降略大于实测数值外，该理论模型能够较好地包含大部分实测数据，且计算沉降曲线在趋势变化方面和实测数值相近。

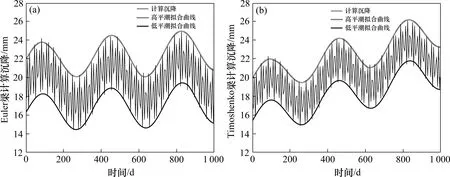
图3 沉降计算结果Fig.3 Settlement calculation results

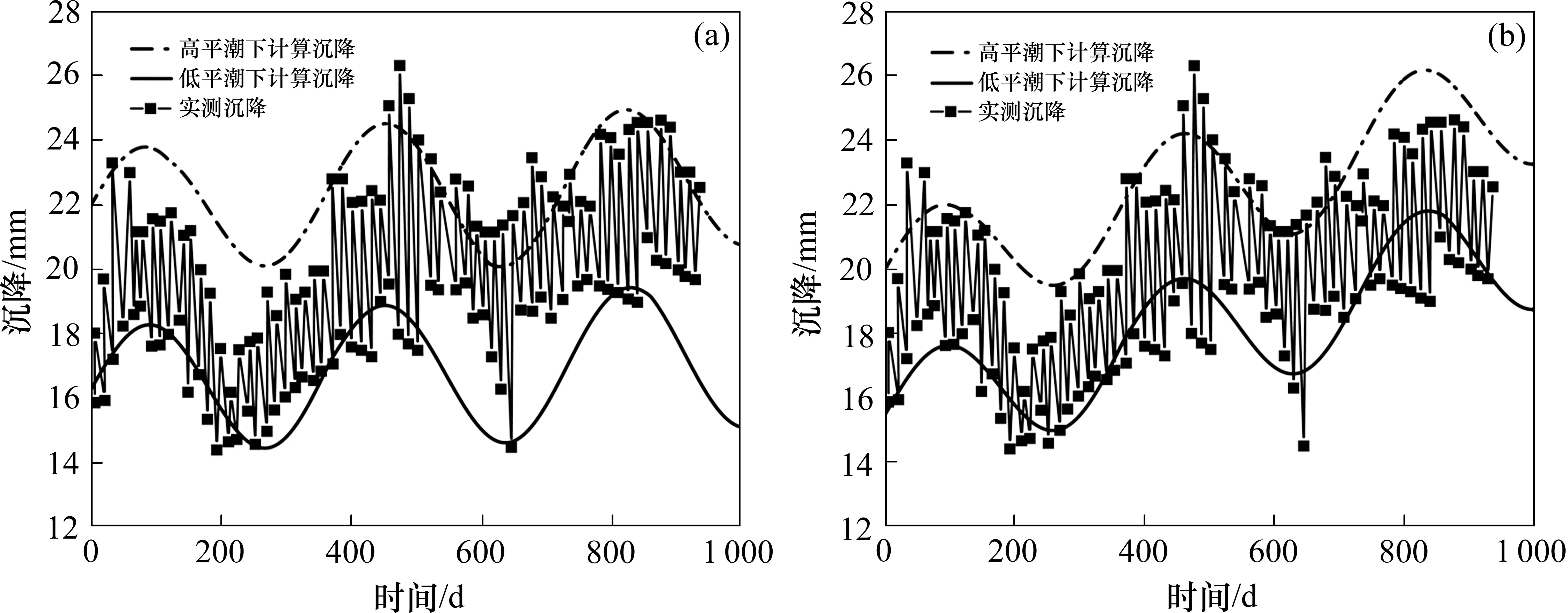
图4 实测沉降和理论沉降对比Fig.4 Comparison of measured value and theoretical settlement

为了更清清楚地观察2种模型下J2接头竖向位移的变化，用Timoshenko 梁模型的计算沉降减去Euler 梁模型的计算沉降，综合对比高平潮和低平潮下的管节计算沉降曲线如图5。进一步通过MATLAB 软件，分析沉管管节接头浮动量，发现以年为周期进行变化，进一步探索2种模型下浮动量的变化率和计算浮动量变化，分析变化趋势，结果分别如图6 和图7。观察图5～7，由于Timoshenko 梁模型考虑了管节接头的剪切变形，在潮汐荷载的反复作用下，由此引起的沉管位移伴随时间的推移逐渐显现，使得管节接头变形无论是在高平潮还是低平潮下，该模型的整体计算沉降值明显比Euler 梁的计算沉降值大。通过图6中标注变化率特征值，Timoshenko 梁模型的变化稍微平缓，这更符合实际工况中管节变形波动程度小而经历时间长的特点。通过图7 比较2 种理论模型的浮动量，发现Euler 梁模型和Timoshenko 梁模型最大年浮动量分别为4.3 mm 和6.6 mm，后者与实测浮动更相近。因此，本文提出的Timoshenko梁模型所模拟的管节沉降能够更好地实测值吻合，最大程度包含实测结果，因此更为可靠。

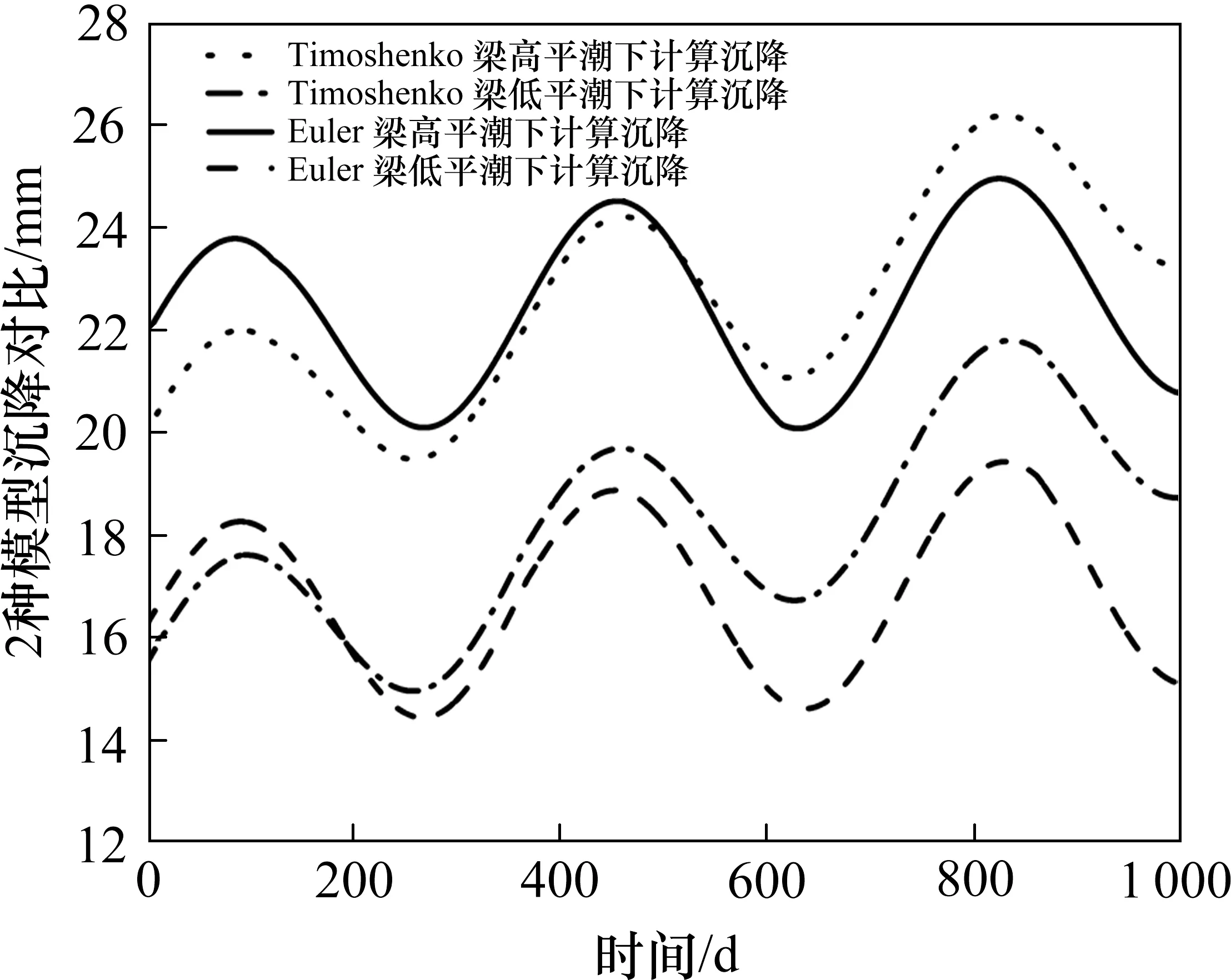
图5 2种模型沉降对比Fig.5 Settlement contrast between the two models

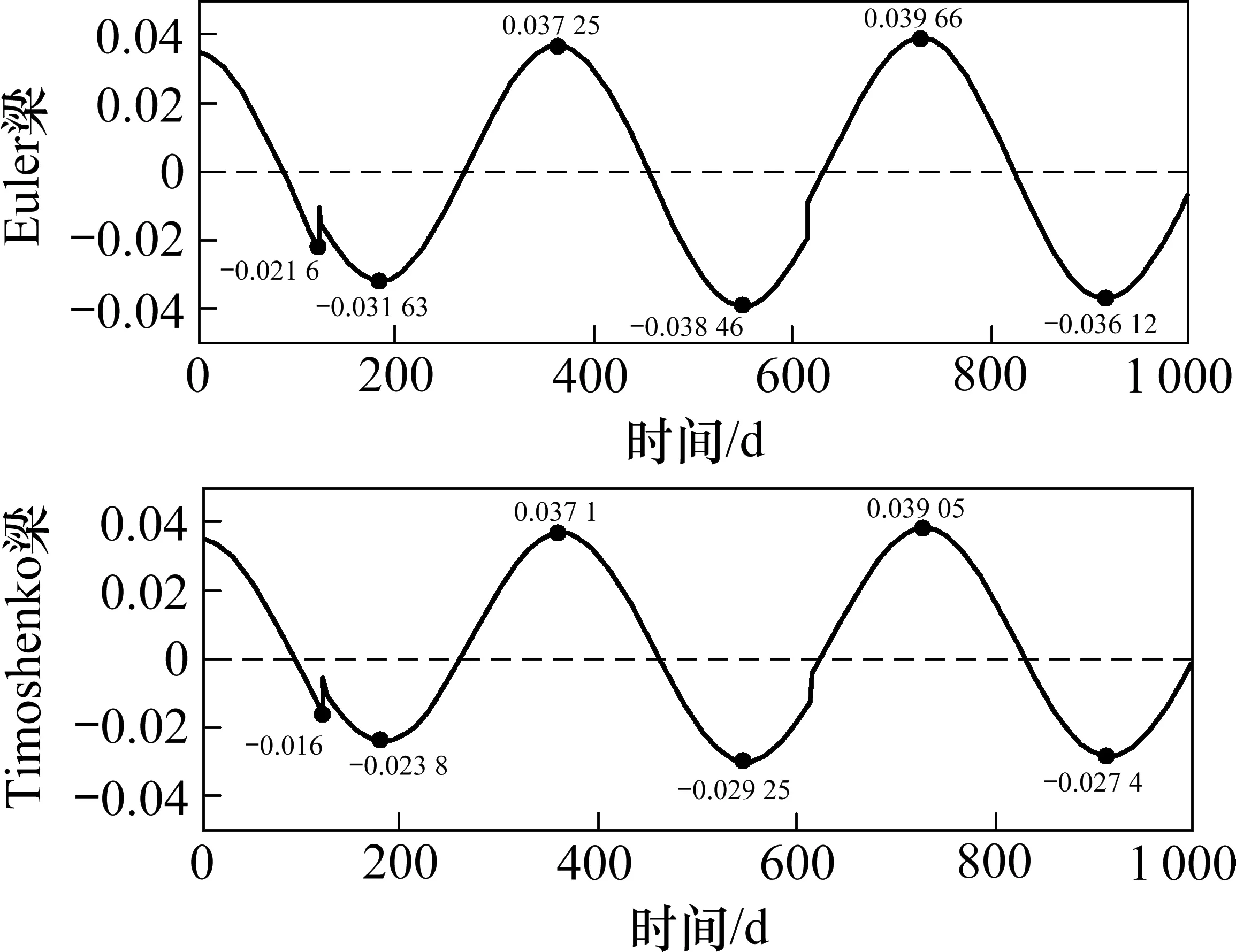
图6 2种模型沉降变化率对比Fig.6 Comparison of settlement rate between the two models

图7 2种模型计算浮动量对比Fig.7 Comparison of calculated float between the two models

4 结论

1)基于Winkler地基的Timoshenko 梁模型同时考虑了管节接头的弯曲变形和剪切变形，更能反映沉管隧道的结构受力特征和沉降变形特点，相较于Euler 梁模型，在管节沉降的前期和中期模拟效果最好，由于考虑了管节接头的剪切变形，在潮汐荷载反复作用下，使得管节沉降伴随时间的推移逐渐显现出来，可以观察到明显的增大趋势，获得了更接近实测数据的计算结果。

2) 在分析管—土相互作用时引入了等效压缩基床参数k(tk)，将其视为伴随时间变化的变量，同时取决于河床下卧土层一维非线性固结沉降的计算精度和潮汐反复荷载的拟合程度，与以往取作固定值相比更符合循环荷载下沉管隧道受到的地基反力作用。

3)沉管管节接头浮动量以年为周期进行变化，Timoshenko 梁模型下的计算年浮动量稍大，且计算沉降变化趋势更为缓和，符合实际工况中管节变形波动小而历时长的特征。

4) Timoshenko 梁模型在管节接头变形后期拟合程度有待改善，这与当前假定土层沿管节纵向均匀分布且忽略隧道运营期间长期受到的车辆荷载以及河床回淤清淤荷载等引起的土层固结沉降等因素有关，下一步将针对性开展相关工作。