静叶倒圆角对叶片气动特性影响CFD 数值方法研究

2022-04-13王姗钟主海江生科吴博

东方汽轮机 2022年1期

王姗，钟主海，江生科，吴博

（东方电气集团东方汽轮机有限公司，四川德阳， 618000）

0 前言

实际加工叶片根顶部与轮盘和围带接触的地方一般有倒角结构，而CFD 计算中一般将叶片根顶部倒角结构简化掉。而很多学者认为，叶片的倒角结构具有控制马蹄涡发展，减小流动损失，减小漏汽损失、控制涡结构、减小叶片与平面接触地方的离心拉应力等潜力，并指出存在一个最佳倒圆角半径使得叶片的效率最高[1-6]。 W Brockett[1]等通过对整圈静叶进行不同半径圆形倒角空气试验，分别在不同叶片表面粗糙度，入口湍流度等对倒角半径为0、 0.5 mm、 1 mm 进行试验，结果发现：相比不带倒圆角结构叶片，最佳倒角半径0.5 mm 可以使静叶效率提高1.4%左右。 Haller B R[3]等发表专利中指出叶片根顶部倒角半径推荐0.2～0.25 乘以喉宽，与文献[1]中提到的 0.25 相符，文中还特别推荐最佳倒角半径为0.233 乘以喉宽（喉宽可用根顶部平均喉宽值）。西安交通大学的石龑[4]等通过对静叶不加倒角结构，动叶根顶部加倒角单级透平叶栅进行CFD 数值计算，计算软件使用FINE-Turbo，计算湍流模型为 Spalart-Allmaras 一方程模型，得出倒圆角结构的存在使得效率降低。

为了研究适用于根顶部倒圆角结构对静叶气动特性的影响的数值方法，本文主要对文献 [1]中的叶片进行CFD 数值计算，并与文献中实验结果进行对比分析，以验证CFD 数值计算的正确性，为计算叶片根顶部倒圆角的CFD 数值计算提供一定的指导作用。

1 叶片提取和型线生成

由于文献对叶片数据的模糊处理，所以首先对叶片轮廓进行还原处理，整个叶高范围内叶型相同，在此选用中部截面使用ATB 程序进行光顺调整，见图1。原始叶型和用ATB 光顺过的型线对比示意图见图2，并使用自主设计TCS 程序对光顺后的型线进行计算，计算截面马赫数分布见图3，可以看出该叶型为前加载叶型。

图1 中部截面ATB 设计界面

图2 原始叶型和用ATB 光顺过的型线对比示意图

图3 中部截面TCS 计算马赫数分布

将拟合的叶型和原始叶型进行三维数值分析，不同截面的表面压力分布见图4。可以看出：拟合的叶型压力分布更均匀，原始型线的压力分布不均匀是由读取文献中的叶型数据有一部分模糊不准确导致叶型不光顺的，但可以看出二者压力分布特性曲线相似，故认为拟合型线与文献中的实验[1]型线相似，下文将使用拟合型线进行三维数值计算和分析。

图4 原始与新拟合型线计算截面压力分布对比曲线图

2 CFD 数值计算及分析

2.1 叶片特性数据

生成的叶片特性数据见表1，其中根径93 mm，叶片高度 17 mm，叶片只数为 50 只。

表1 叶片特性数据

2.2 CFD 数值计算模型及边界条件

为了数值计算与文献[1]中提到的实验条件更相符，本文CFD 数值计算模型为不带动叶的单通道静叶叶栅通道，见图5。网格划分使用NUMECA 中的Autogrid5 模块，倒圆角结构网格划分使用正交性较好的蝶型网格结构，见图6。

图5 计算模型

图6 蝶型倒圆角网格

表2 为三维数值计算的边界条件，其中Pratio为压比，并且Pratio=入口总压/出口静压。

表2 计算边界条件

为便于比较分析，采用与文献[1]中相同方式评估叶栅性能，静叶栅效率计算公式为其中：ν 为静叶出口速度，νid为静叶出口等熵速度。

分别用CFX 和NUMECA 软件中的不同计算模型对不同根顶部倒圆角进行数值计算分析，表3为压比为1.4 时的叶栅效率计算结果。实验[1]中，r=0.5 mm 时效率最高， r=1.0 mm 效率高于无倒圆角，见表 4。对比表 3-4，可以看出：不同计算软件和计算模型条件下，倒圆角半径r=0.5 mm 时叶栅效率最高，与实验[1]结果相符，但NUMECA 的k-ω 模型计算结果除外；其余计算结果均表现出无倒圆角时效率高于r=1.0 mm 的效率，与实验[1]结果相反；不同倒圆角半径之间，数值计算的差异较实验[1]结果小。比较之下， NUMECA 的 k-ω 模型计算结果与实验[1]结果趋势更接近。

表3 不同软件模型不同倒圆角半径下的计算效率(压比1.4）

表4 实验值[1]

为了验证k-ω 模型的准确性，对压比1.2 的情况进行计算，见表 5。可以看出实验[1]中，倒圆角0.5 mm 效率比无倒圆角高0.5%左右，倒圆角1.0 mm 比无倒圆角效率高0.4%左右。对比表5 中数值计算的数据，验证了NUMECA 中的k-ω 对叶片倒圆角半径不同时，计算效率与实验[1]的趋势的一致性。

表5 NUMECA k-ω 模型对不同倒圆角半径下的计算效率(压比1.2）

从以上计算可知，数值上NUMECA 中的k-ω模型对带倒圆角结构的计算更精确些，故选NUMECA 软件中的k-ω 模型进行计算。

2.3 CFD 数值计算结果及分析

图7 为不同倒圆角下，压比Pratio=1.2 时的数值计算和实验[1]效率的结果，可以看出：在倒圆角半径r=0.5 mm 时效率最高， r=1.0 mm 时效率有所下降，与实验结果趋势相符。

图7 不同根顶部倒圆角范围下的效率曲线（CFD 计算条件Pratio=1.2）

图8 为不同压比下，对倒圆角半径r=0 mm 的数值计算和实验[1]效率曲线。可以看出在亚音速流动下，随压比的升高，效率提升。与实验结果趋势相符。

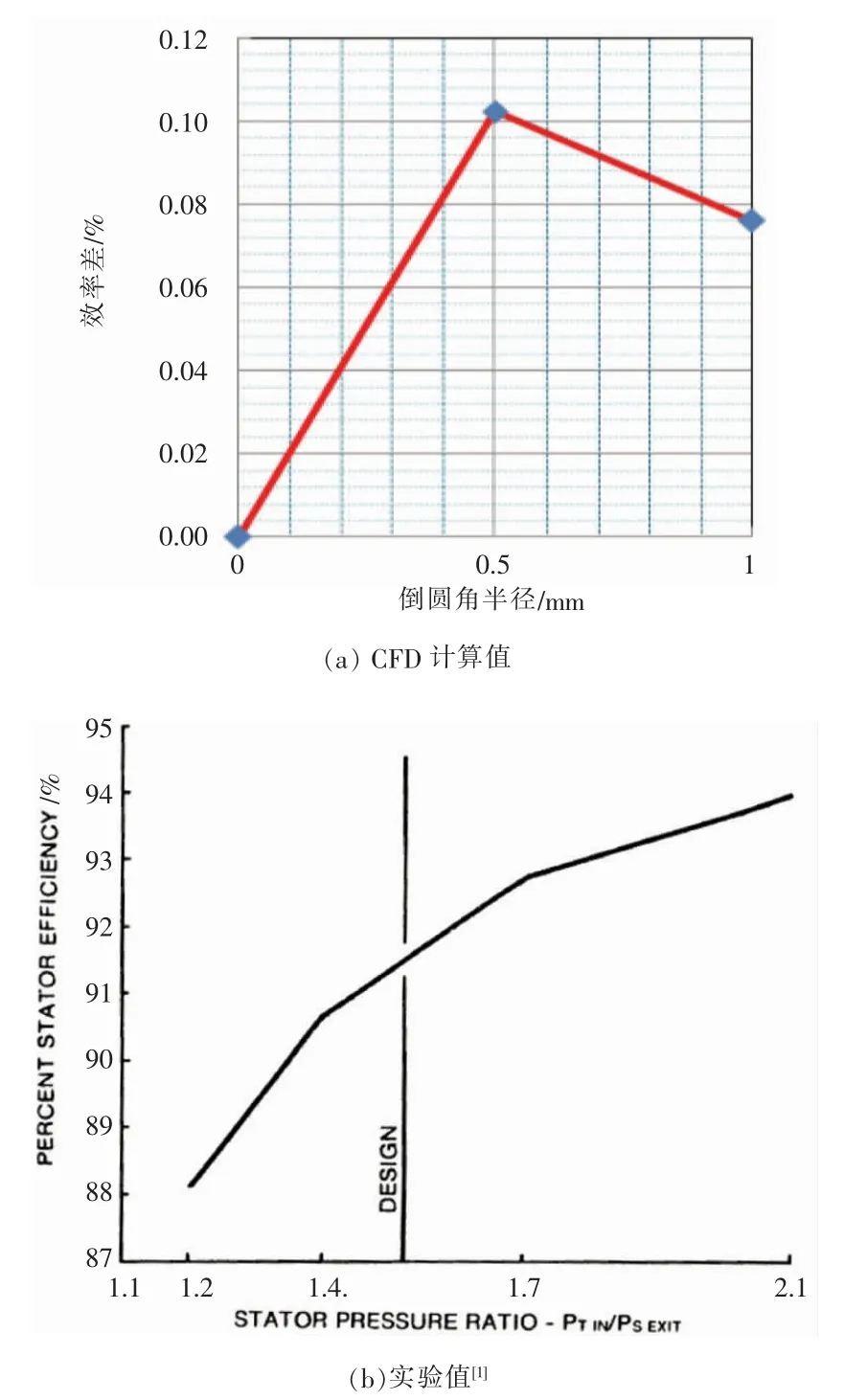
图8 不同压比下的效率曲线（CFD 计算条件r=0）

2.4 根顶部倒圆角CFD 数值具体分析

不同倒圆角半径，选取压比1.2 进行计算。由前文可知，倒圆角半径r=0.5 mm 时效率最高。本小节将具体分析不同倒圆角半径下的流场等信息。

图9-11 分别为 r=0、 0.5 mm、 1.0 mm 时不同截面的马赫数分布图。从图中可以看出：叶栅根部马赫数大，顶部马赫数小；根顶部带有倒圆角的叶片前缘和尾缘半径增大使得前缘和尾缘的汽流流动情况稍有不同；带倒圆角结构的叶片前缘半径更大，攻角适应性更好；而对于尾缘部分，如果倒圆角半径过大，尾迹流更长，导致尾迹损失急剧增加，因此倒圆角半径存在最佳值。