END序列样本VaR核估计的Bahadur表示
2022-04-12王文琴
王 巍,朱 勇,王文琴
(池州学院 大数据与人工智能学院,安徽 池州 247000)
风险价值(VaR)是衡量金融市场风险的主要指标,它在风险度量和动态监管方面具有特殊的优势,因而已被广泛接受。早期的VaR估计主要是对资产回报率的分布进行参数估计,但资产回报率的分布往往是未知的,因此在计算VaR时常常因模型的错误设定而出现偏差。近年来,一些学者给出了VaR非参数估计,使VaR非参数估计不再受回报率分布的约束,因此VaR非参数估计受到了众多学者的广泛关注。目前,人们在研究α-混合、负相协(NA)、负相依(NOD)等序列样本的VaR非参数估计方面已取得了许多成果[1–8]。在此基础上,我们以广义负相依(END)样本为研究对象,利用END序列的性质及其指数不等式研究了VaR核估计的性质,给出了VaR核估计的Bahadur表示,得到END样本VaR核估计的强相合性及收敛速率。
1 相关概念及引理
VaR是指给定概率水平下一定时期内金融资产的最大损失,其统计学定义为vp=inf{u:F(u) ≥p},其中F(u)是金融资产在第t个时间段内资产回报率Xt的分布函数,p为给定的概率水平。VaR概念提出后,一些学者对VaR估计量产生了浓厚的兴趣。GOURIEROUX等[9]给出了VaR核估计量,并给出了资产回报率序列的分布函数F(x)的核估计
令Fn,h(x) =p,通过求的反函数就可得到风险价值vp的核估计量vp,h,即VaR核估计量。
END随机变量序列由LIU提出,它是一类比NOD序列更弱的相依序列。
定 义[10]:X1、X2、X3、 ⋅⋅⋅、Xn为END随 机 变 量是指 随机 变量X1、X2、X3、 ⋅⋅⋅、Xn满 足以下条 件:存在正常数M,当n≥ 1时,对于任意的xi∈(− ∞, +∞)(1≤i≤n), 满足P(X1>x1,X2>x2,X3>x3,⋅⋅⋅,Xn>xn)是END随 机变量,则称序列 {Xn,n≥1}是END序列。
下面给出所需要的相关引理。
引理1[10]:若 {X,n≥1}是END随机变量序列,n{fn(⋅),n≥ 1}为非降函数(或非增函数),则{fn(Xn),n≥1}仍是END随机变量序列。
引理2[11]:若 {Xn,n≥1}是END随机变量序列,那么对于任意t>0,有

引理3[12]:设X为随机 变 量,EX= 0,|X|≤b,b为正常数,那么对于λ>0,有

其中,λb≤C≤1。
引理4:设 {Xn,n≥1}是END随机变量序列,且有EXn=0。 对 于 每 个i≥ 1,|Xi|≤b,b为 正 常 数,那 么对于任意有


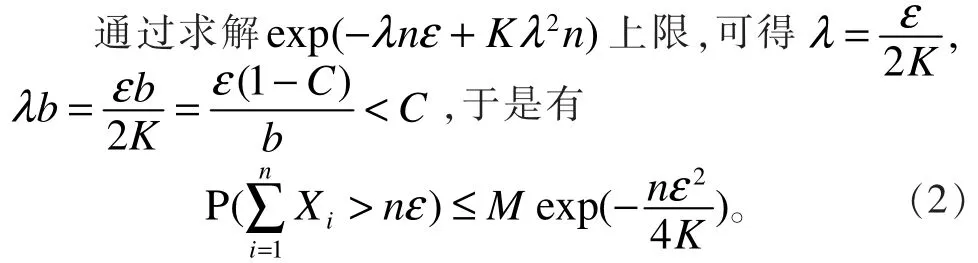
同理可得
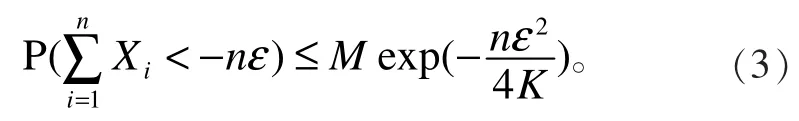
由式(2)和式(3)可知式(1)成立。
引理5[13]:若F(X)为右连续的分布函数,则其反函数F−1(t)是非降左连续函数的充分必要条件是当x≥F−1(t)时,有F(x)≥t。
2 主要结果及证明
以下约定C为正常数,且在不同的地方可以表示不同的值, [x] 表示取不超过x的最大整数值,logx=lnmax(x,e)。
命题1:假设 0
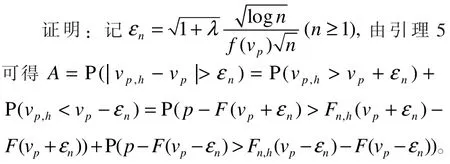

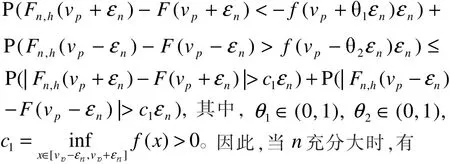

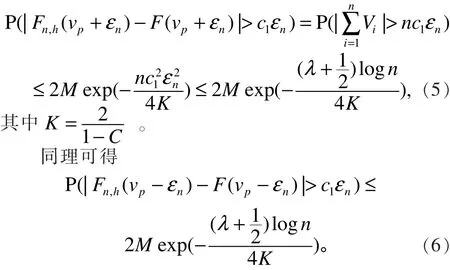
结合式(5)和式(6)可得
令λ=4K,则由式(7)可得

由Borel-Cantelli引理可知, |vp,h−vp|<εn以概率1成立。

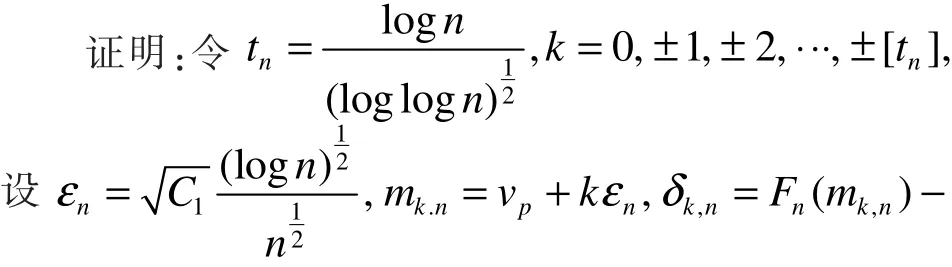

及
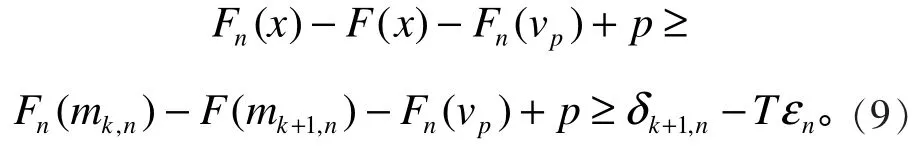
由式(8)和式(9)可得
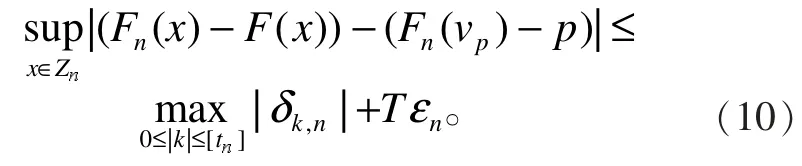
对于任意给定 k ,易知

类似可得,当 n充分大时,有

令C1= 17 K1,则 由 式(11)、式(12)和 式(13)可得,当 n 充分大时,有

定理2:若定理1的条件成立,则存在常数 C2,当n无限大时,不等式以概率1成立。


证明:由定理1可得,当 n→∞时,有
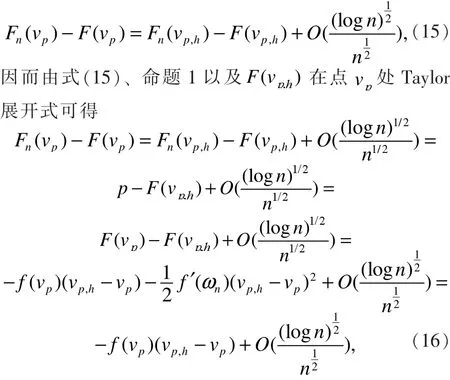
其中, ωn为介于 vp,h和 vp间的随机变量。由式(16)可得,当 n→∞时,有
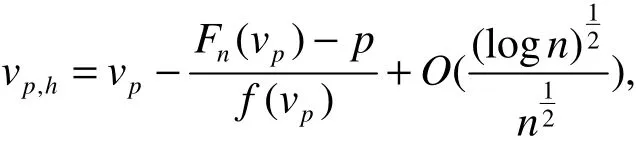
从而定理3结论成立。
3 结论
在本文中,我们利用END序列的性质及其指数不等式研究了END序列样本VaR核估计的性质,证明了VaR核估计的强相合性及收敛速率,给出了VaR核估计的Bahadur表示。我们还将文献[1–2]中混合样本VaR核估计和线性核分位数估计的研究结果推广到END样本,给出了END样本的VaR核估计量的性质及Bahadur表示。
与文献[4]的结果相比,我们在研究END样本的VaR核估计时,获得了与样本分位数估计相似的收敛速率,并在G(x) =I(x≥0)时导出了与文献[4]一致的退化形式,所得结论更具一般性。
