钢-混组合梁桥工型截面设计合理性研究
2022-04-12曹前进
任 炜,赵 青,曹前进
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
钢-混凝土组合梁是将受压混凝土和受拉钢梁通过剪力连接件组合在一起的新型桥梁模式[1],该模式桥梁能够充分发挥两种材料的长处。20世纪50年代,欧美各个国家开始对组合梁进行研究。欧洲于1985年颁布《欧洲规范4》(EC4),提出了钢与混凝土组合设计总则与桥梁设计规则。参照国外规范,2015年我国制定了《公路钢混结构桥梁设计规范》(JTGD 64—2015)。目前,我国已有不少学者对钢混桥的技术性能进行了研究。安然等[2]研究了施工阶段考虑滑移界面的梁刚度折减,陈正星等[3]研究了组合梁桥负弯矩区段设计,冯联武等[4]针对钢-混组合桥面收缩徐变产生的应力分布进行了理论计算,但是对工形截面设计参数的研究还较少[5-8]。本文依照组合梁特点,采用有限元软件进行分析,得出相关截面参数的最佳值,为相关研究人员提供理论帮助。
1 工程概况
某一典型45 m+55 m+45 m公路钢—混组合双工字钢梁桥的相关参数如下:桥面板宽为12.30 m,桥面板厚为0.25 m,采用C40混凝土,上翼缘板宽为800 mm,上翼缘板厚为32 mm,梁高为2.5 m,腹板宽为0.5m,腹板厚度为50 mm;下翼缘板宽为90 mm、厚为34 mm。双梁采用相同截面形式布置,且两钢梁之间布置横隔板。横隔板上下翼缘的宽度和厚度均为20 mm,腹板宽为0.5 m。本案例钢材材料采用Q345qD。
2 参数控制及模型建立
2.1 参数控制
因不同梁高时整体结构受力情况不同,故在保证合理梁高的基础上,还要考虑腹板高厚比对工型梁上翼缘应力的影响。本桥梁为等截面桥梁,高跨比为22,腹板高厚比为50。本研究采用控制变量法研究两种工况条件下梁高对梁应力和挠度的影响。工况一:只改变梁高,不改变腹板厚度,即高跨比和高厚比同时改变。工况二:同时改变梁高和腹板厚,但保证在高跨比改变的同时,高厚比保持不变。两种工况条件下梁高和腹板厚见表1。

表1 两种工况条件下的梁高和腹板厚数据
2.2 有限元模型建立
本文采用MIDAS CIVIL进行模拟,考虑到采用一般方法建模时需要用弹性连接钢-混桥的剪力连接件,建模工程量巨大,故采用施工阶段联合截面法进行建模,建立的钢-混桥上部结构MIDAS模型如图1所示。这种方法可以采用不同的材料和单元分别定义桥面板和钢梁,在模型中各个剪力连接件默认为完全连接,混凝土板与钢梁之间不存在相对滑移,且在荷载作用下钢梁处于弹性体状态。

图1 钢-混桥上部结构MIDAS模型
桥全长为145 m,分为45 m+55 m+45 m三跨,共有节点168个、单元182个,桥梁平面布置如图2所示。上部结构采用钢筋和混凝土两种材料,桥面板采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG 3362—2018规定的C40混凝土。该材料的属性如下:弹性模量E=3.25×107 kN/m2,泊松比μ=0.2,密度ρ=2400 kg/m3。主梁及横梁采用Q345qD钢材,其材料属性如下:弹性模量E=2.06×108kN/m2,密度ρ=7.85 g/cm3,泊松比μ=0.31,阻尼比为0.02。荷载包括钢梁自重、二期荷载以及汽车公路I级活荷载。模型整体约束如表2所示。

表2 支座约束

图2 桥梁平面布置
3 有限元软件模拟钢梁强度和刚度讨论
在不同变量(仅改变高跨比和同时改变高跨比和腹板高厚比)下,针对架梁和铺装混凝土阶段按照表1所示工况分别进行分析。
3.1 工型截面钢梁强度研究
钢-混组合梁桥的施工主要分为架梁、铺装、二期恒荷载施工、收缩徐变4个阶段。在架设钢梁阶段,整体一般只有自重影响,在铺装混凝土阶段钢梁不仅受到钢梁自重影响,还受到混凝土竖向均布压力荷载。在架梁期和铺装期仅改变梁高时钢梁应力值如图3所示。

图3 不同时期钢梁应力
由图3知,架梁期和铺装期不同梁高下的最大拉应力分别为:当梁高为3 m时,最大拉应力分别为28.5 MPa、-14.3 MPa;当梁高为2.5 m时,最大拉压应力分别为33 MPa、-16.5 MPa;当梁高为2.12 m,最大拉压应力分别为37.8 MPa、18.9 MPa;同一桥梁、同等条件下,高跨比越小钢梁应力反而越大,但是应力增减处于可控制范围。
在仅改变梁高保持腹板高厚比不变情况下,对上述两个时期的钢梁应力值分别进行拟合,拟合结果如图4和图5所示。

图4 架梁期钢梁上缘应力

图5 铺设混凝土期钢梁上缘应力
3.2 在腹板高厚比不变情况下钢梁强度分析
由3图知,不管在架设钢梁阶段还是在铺装混凝土阶段,仅改变梁高时,钢梁上翼缘应力值总体上处于稳定状态。
由图4和图5知,在保持腹板高厚比不变的情况下,改变梁高(即改变高跨比),钢梁上翼缘应力依然遵循着“梁越高,应力越小”的规律。在架设钢梁阶段,梁高从3 m降到2.29 m,腹板厚度随之相应减小,高跨比从1/18→1/24,钢梁上翼缘应力随之增大,涨幅相对稳定;当梁高从2.2 m降低至2.12 m时,高跨比从1/25→1/26,此时钢梁应力达到最大值,并出现应力激增现象;同时在铺设混凝土阶段,梁高从3 m降到2.29 m,高跨比从1/18降低到1/24,平均最大拉应力增大8.5 MPa,最大压应力增大4.7 MPa;当梁高从2.2 m降到2.12 m时,最大拉压应力增加过大,但最大应力值依然小于Q345qD的屈服强度极限值。
当梁高从2.2 m降至2.12 m时,高跨比从1/25降至1/26,如果此时依然保持腹板高厚比不变,钢梁上翼缘的应力均会有不同程度的激增,在施工阶段可能会出现应力突变,存在结构安全隐患。
由图4和图5可知,在梁高2.2 m降至2.12 m时,不论在哪个施工阶段,钢梁上翼缘应力均会发生应力突变,高跨比会影响钢梁上翼缘应力。现在分别选取梁高为2.50 m、2.29 m、2.12 m,在不同高跨比和腹板高厚比情况下进行分析。由于图4和图5曲线走势几乎相同,现对架梁期单、双变量应力增长率η(图6)做分析(铺装期分析方类似,不作赘述)。双变量指指只改变梁高,腹板厚度依然保持不变,应力
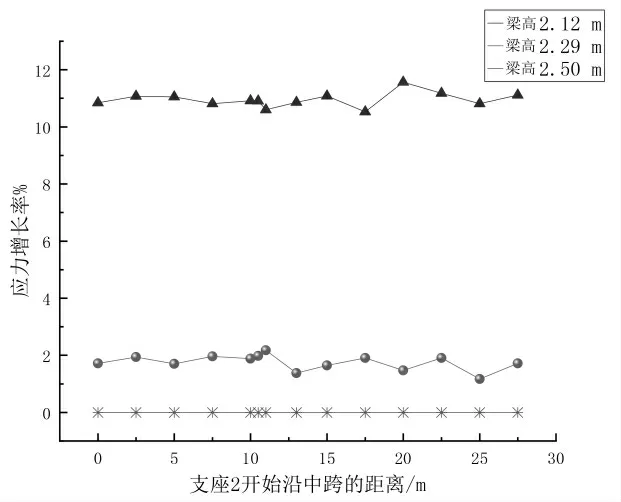
图6 单、双变量应力增长率分析图
由图6可知,梁高在2.50 m时,由于此时单、双变量所对应的钢梁应力值相同,且η=0;在梁高为2.29 m时,η值普遍集中在1%~2%之间,说明在梁高一定的情况下,改变腹板高厚比,钢梁上缘应力值并不会发生太大改变,钢梁上缘应力主要受高跨比的影响;当梁高降低至2.12 m时,降低高跨比,钢梁上缘应力依然会持续增大,但是如果改变腹板高厚比,即腹板厚度随之减小,钢梁上翼缘应力会发生突变,单双参数下的钢梁应力值差值变大(η集中在10%~12%之间),此时应力值主要由腹板高厚比起主导作用。在不确定梁高情况下,在降低梁高时,不可一味减小腹板厚度。
3.3 工型截面钢梁刚度研究
高跨比和高厚比对钢梁强度均会产生不同程度的影响,即在不同工况下下,应力会产生改变。为保证梁结构的可靠性,还需考虑不同高跨比和高厚比对钢梁刚度的影响。在公路I级荷载作用下桥梁的挠度变化情况如图7所示。

图7 公路I级荷载作用下桥梁的挠度
由图7知,在公路I级荷载作用下,桥梁的最大挠度处于跨中位置。在模拟中,通过改变截面高跨比和高厚比,对单、双参数条件下的挠度值进行对比。在考虑单参数(梁高改变,腹板高厚比保持不变)情况下,取出不同梁高下跨中处的最大挠度值,并对最大挠度值进行拟合,拟合结果如图8所示。

图8 单参数下跨中最大挠度值变化
在梁高从2.12~3.0 m改变时,跨中处的最大挠度呈减小趋势,反过来说,减小梁高,跨中处的最大挠度值呈增大趋势。
在考虑双参数(改变梁高和腹板高厚比)情况下,采用Origin 2018对不同梁高下跨中处的最大挠度值进行拟合,拟合结果如图9所示。
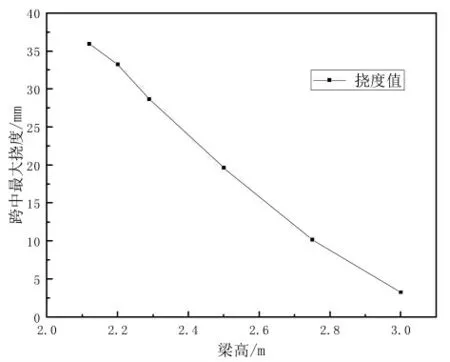
图9 双参数下跨中最大挠度值变化
由图9知,减小梁高和腹板高厚比,跨中挠度值依然还会增大,但是相对于单参数下的挠度,跨中挠度增大趋势并不是特别明显。当梁高减小到2.29~2.12 m时,跨中处的最大挠度值增量会明显减小,腹板厚度对挠度值的影响较大。
4 结束语
本文利用MIDAS CIVIL有限元软件对钢-混组合梁的梁高和腹板厚对钢-混组合梁强度和刚度的影响,得到了在仅改变梁高参数和同时改变梁高和腹板厚参数两种工况条件下,钢-混组合梁在不同施工阶段钢-混梁应力变化规律和挠度变化规律,得出了在满足强度和刚度条件下梁高和腹板厚的取值范围,但对最佳梁高、高厚比等钢-混组合梁的结构参数仍需进行深入的研究。
