基于机器学习的湿化仪温度预测建模与仿真

陈龙龙，李 凌

(沈阳化工大学 信息工程学院，辽宁 沈阳 110142)

0 引言

随着人们生活质量的提高以及现代医学的高速发展，呼吸湿化治疗仪在现代生活中得到了广泛的应用。当下正值新型冠状病毒(COVID-19)肆虐全球之际，呼吸湿化治疗仪在这场防疫保卫战中发挥了重要作用。就本质而言，新冠肺炎可以被看做为一种呼吸道疾病，治疗过程中往往需要持续加入高流氧。高流量湿化治疗仪作为一种新型呼吸、湿化仪器，已经被列为紧缺型医疗器械。相比于传统的湿化治疗仪，该设备可以为患者提供(10 L/min～80 L/min)的高流量、恒定氧浓度(21%～100%)、高湿度的空氧混合气体。通过持续高流氧的流入，可以使病患产生呼吸末正压[1]、对上呼吸道生理死腔具有很好的冲刷效果、经过加温加湿后的气体不但可以使黏液纤毛的清除作用得以保持，同时也具有降低患者上气道阻力和呼吸功等作用，使患者的呼吸功能得到改善[2]，对轻中度急性呼吸衰竭、呼吸窘迫综合症的治疗效果明显，同时也对诸如内窥镜检查等具有很好的辅助作用[3]。设备示意图为图1所示。

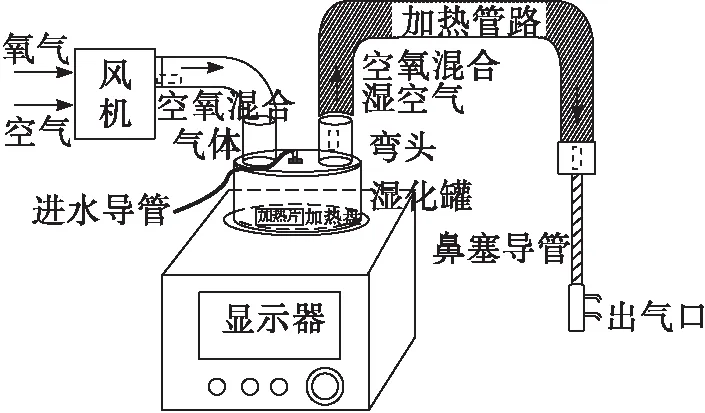
图1 高流量呼吸湿化治疗仪示意图

该设备最基本的工作方式为，首先进行的是空氧混合气体的通入，其次是通过加热盘，对由进水导管加入的蒸馏水进行加热，产生的水蒸气进入弯头，最后再由弯头内部的加热装置进行加热，然后可以通过呼吸面罩等装置进入患者体内。

出气温度是衡量湿化仪治疗效果的关键性指标，合适的出气温度不仅可以湿化和湿润气道黏膜[4]、使纤毛运动保持清洁功能，还可以让患者感到更加舒适。但是，由于设备在运行过程中，出气温度会受到多种因素的影响，因而无法采用传统方法建立温度系统的机理模型。目前，人工智能技术的应用为制造行业的装备设计与革新提供了一定的技术支撑。以机器学习，特别是深度学习为核心的人工智能技术，得到了广泛推广和应用。随着信息技术的发展，设备运行过程中的各项参数得到记录，这些数据清楚的记录了呼吸湿化治疗仪的运行状态，通过挖掘这些数据信息，结合人工智能技术，分析系统的运行工况，为系统的优化提供基础。

通过大量的离线数据进行数据建模，很好的避免了机理建模复杂且难以实现的问题，且模型相比于机理模型更加准确，可以很好地反映出实际对象的运行状况。该实验使用的数据来源于国内某企业高流量湿化仪治疗仪的运行数据，从数据建模方向入手，分别采用多元线性回归、随机森林、支持向量机等机器学习算法对高流量湿化治疗仪温度系统进行建模，并对模型进行测试。仿真结果表明，三种方法皆可以实现对出气温度的预测，相比较而言，随机森林的预测效果要明显优于另外两种算法。

1 数据采集准备及预处理

1.1 数据采集

该文所用数据来源于沈阳某呼吸机企业实际运行的数据，数据采样间隔为1 s，采集时间为12月某天设备稳定运行时的数据，选取10 L/min和80 L/min两种工况下的数据作为此次对比实验的样本。样本数据主要包含8项指标，如表1所示，基本涵盖了湿化仪出气温度及其主要影响因素[5]。

表1 湿化仪特征参数

1.2 数据准备及预处理

1.2.1 输入、输出变量选取

(1)输入变量的选取

输入变量的选取对此次实验的结果至关重要[6]。该文通过查阅有关文献、结合设备的实际运行情况，综合考虑了对温度影响的各种因素，考虑到数据的可采集性和精确性，选取进气温度、加热片、加热盘、功率、流量、设定流量、作为输入变量。

(2)输出变量的选取

实验选取湿化治疗仪的出气温度作为输出变量。

1.2.2 数据的预处理

(1)异常数据处理

对于出气温度的预测需要以湿化治疗仪大量历史数据作为依据，数据集的好坏很大程度上决定了结果的优劣。数据的收集是一项极其复杂的工作，容易受到各种因素的干扰，经常会出现一些异常数据，异常数据的存在通常会导致模型精度的降低。出于模型的精度考虑，通常需要剔除异常数据[7]。剔除异常数据利用3σ准则：对于样本X={x1，x2，…xn}，标准差为：

(1)

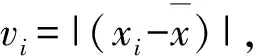
(2)数据标准化

标准化采用了min-max标准化法，对于数据集中的每一个值x，其标准化公式为[8]：

(2)

其中：xscale，x，xmax，xmin分别为归一化之后的值、原始值、最大值与最小值[9]。

2 系统建模

2.1 多元线性回归

回归分析(Regression Analysis)是一种在统计学上比较常见的分析数据的方法，主要在于通过分析，了解每个变量之间存在的关系。线性回归假设数据具有一定的线性关系，且线性关系越强，效果越好。根据上述分析和相关数据表明，多种因素均会对出气温度产生影响。为了能够根据这些因素对出气温度进行预测。该文首先尝试构建基于多元线性回归的出气温度预测模型。多元线性回归模型构建过程如下：

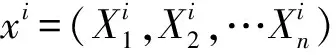
y=θ0+θ1x1+θ2x2+…θnxn

(3)

多元线性回归模型的求解思路与普通线性回归类似，即通过训练数据样本，找到对应的参数θ=(θ0,θ1,θ2…θn)，作为一种列向量，可以通过虚构第0个特征x0，使它恒为常数1，则在公式推导时，结构会更加整齐：

(4)

将上式(4)改写成向量点乘的形式：

(5)

因此，可以把目标写成向量化的形式：

y=Xθ

(6)

在已知训练数据样本x，y的情况下,找到向量θ，使(y-x·θ)T(X·θ)尽可能小。便可得到多元线性回归的正规方程解：

θ=(y-X·θ)-1XTy

(7)

2.2 随机森林算法

随机森林算法是使用一种称为 bagging 的算法将许多决策树组合在一起，以投票机制进行分类的有监督学习算法，训练速度好，泛化能力强都是它的优势。

2.2.1 决策树

决策树，也称为分类和回归树(CART)，它可以用来描述输入一组特征后输出的不同类或值。决策树因为具有树结构，其中所有的内部节点都代表着一种属性测试，分支则代表测试输出，子叶点表示结果[10]。

假设X是一个包含m个特征的输入变量，Y是输出值，Sn是一个包含n个观测值(Xi，Yi)的训练集，其中：

Sn={(X1,Y1),…(Xn,Yn)},X∈Rm,Y∈R

(8)

在训练过程中，算法在每个节点上对输入进行分割。首先，CART 算法将输入空间X递归地划分为两个不同的分支:

{Xjd},j∈{1,…,m},d∈R

(9)

为了更好地划分，(j,d)应使代价函数最小化，通常是子节点方差，节点p的方差定义为：

(10)

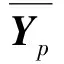
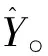
(11)

2.2.2 随机森林

随机森林是一种将多棵决策树组合在一起的集成方法。采用Bootstrap 采样方法

从原始数据集中提取一些样本，然后根据每个Bootstrap样本建立决策树模型，其次通过对多种决策树的预测进行整合，最后通过投票得到最终结果[11]。

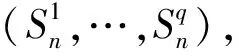
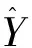
(12)

随机森林的实现过程大致如下：

(1)原始训练数据集为Sn，利用Bootstrap方法提取有n个观测值的q数据集，构建q决策树。

(2)有m个变量，在每棵树的每个节点随机 选取mtry变量。然后在mtry变量中选择分类能力最好的变量，得到最佳的分割点。

(3)每棵树不需要任何改动就能生长到最大程度。

(4)结果树构造一个随机森林来预测新数据，结果由随机森林中的树投票决定。

2.3 支持向量机

SVM算法经常被用于解决分类及回归问题。该算法是基于统计学理论、Vapnik-Chervonenkis Dimension(VC 维)

理论基础上形成的，通过有限样本在模型中的学习情况，寻求最佳方案。针对非线性不可分问题，则通过核函数将数据由低维空间映射到高维空间，进而实现高维可分[12]。

SVM的基础是寻找在线性可分条件下的最优分离超平面，首先给定一个样本集S={(xi，yi)}；i=1，…，n,x∈Rd,y∈{+1，-1}}，其中xi为数据，yi为数据所属类别。

SVM的原始问题可表示为：

(i=1,…,n,C>0,εi≥10)

(13)

式中：ω为权重向量；b为偏置向量；ξ为松弛因子；C为惩罚因子[13]，可通过调节该参数实现算法复杂度与分类精度的平衡。

通过求 Lagrange 函数的极值点得到原始问题的最优解。通过引用 Lagrange 乘子算法，将上述原始问题转化为对偶形式[14]，表示为：

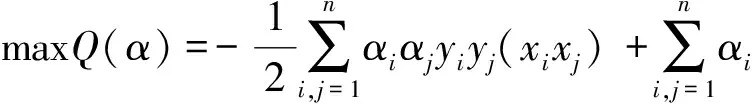
(14)

式中：α为拉格朗日乘子。

对于非线性不可分样本，SVM 通过非线性映射将样本(xi,xj)映射到核函数K(xi,xj)指引的高维特征空 间中，在特征空间中实现内积运算[15]；故在非线性不可分情况下，公式(14)可表示为：

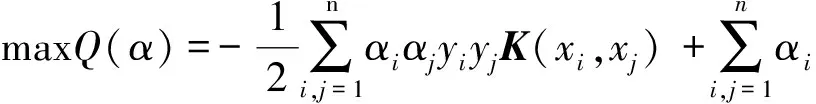
(15)

比较常见的核函数K(xi,xj)有径向基核函数(RBF)、多项式核函数及Sigmoid核函数等。核函数该怎样选择，样本数据在进行回归估计时都有相应效果最好的核，但在缺少先验知识过程时，多项式核函数无法进行前期的正交化过程，而且该样本数据不满足Sigmoid核函数的半正定条件[16]。RBF 主要是通过分析训练样本距原点距离的实值函数，通过分析讨论，该实验选择 RBF 作为 SVM 分析的核函数，其数学表达式为：

(16)

式中:σ为置信范围;γ为间隔。

3 模型验证与仿真

通过将原始数据集进行划分，选取75%的数据进行模型训练，其余25%的数据进行测试，以检验模型的准确性。本部分主要是基于以上算法建立的三种模型，选用10 L/min和80 L/min两种工况下的数据集，对多元线性回归、随机森林和支持向量机三种预测模型进行模型验证及效果评估[17]。

3.1 基于多元线性回归的出气温度预测仿真

利用Python进行编程，基于多元线性回归对出气温度进行预测，预测结果如图2、图3所示，拟合得到的回归方程如下：

y1=4.726+0.585 9x1+0.289 4x2-0.001 0x3

-0.027 6x4+0.054 79x5-0.943 5x6-0.000 1x7

(17)

y2=31.418+0.106 9x1+0.000 8x2-0.000 2x3

-0.000 5x4-0.000 3x5+0.008 8x6+0.000 1x7

(18)

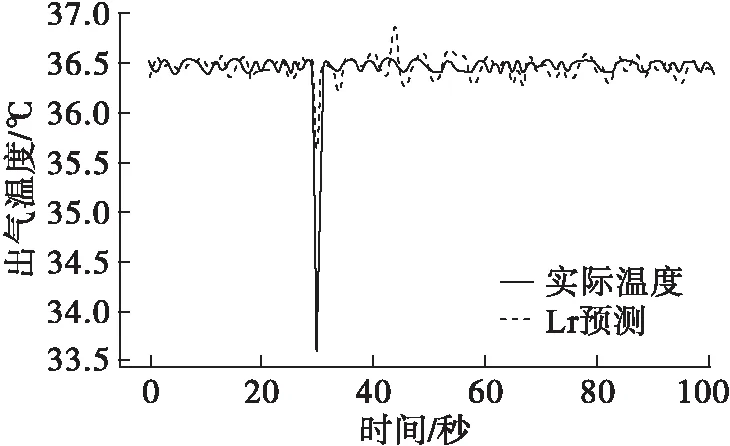
图2 10 L/min工况下出气温度预测图

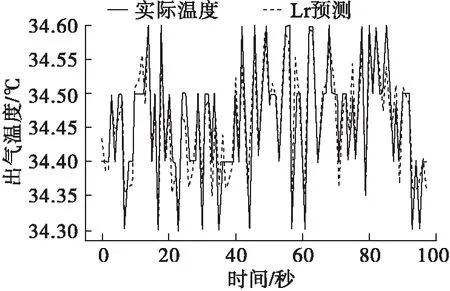
图3 80 L/min工况下出气温度预测图

3.2 基于随机森林的出气温度预测仿真

利用Python进行编程，基于多元线性回归对出气温度进行预测，预测结果如图4、图5所示。

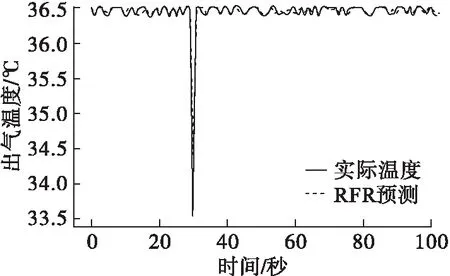
图4 10 L/min工况下出气温度预测图

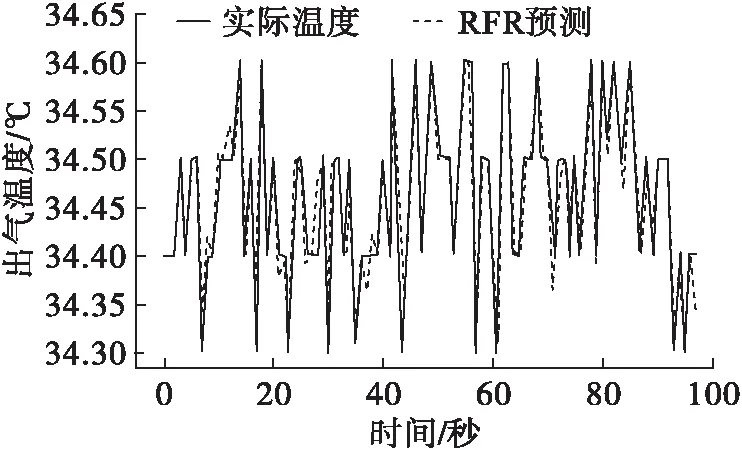
图5 80 L/min工况下出气温度预测图

3.3 基于支持向量机的出气温度预测仿真

利用Python进行编程，基于支持向量机对出气温度进行预测，预测结果如图6、图7所示。

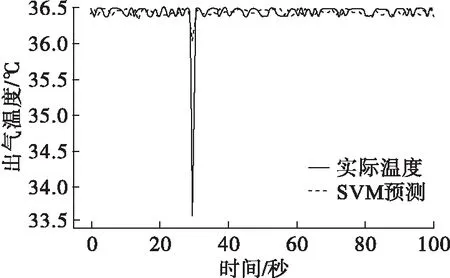
图6 10 L/min工况下出气温度预测图

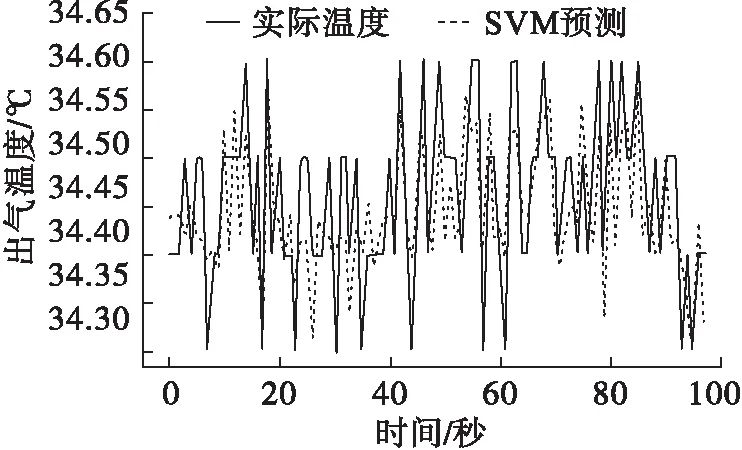
图7 80 L/min工况下出气温度预测图

4 性能对比分析

分别将10 L/min和80 L/min两种工况下的数据分别输入到多元线性回归、随机森林和支持向量机模型中进行预测对比分析[18]。

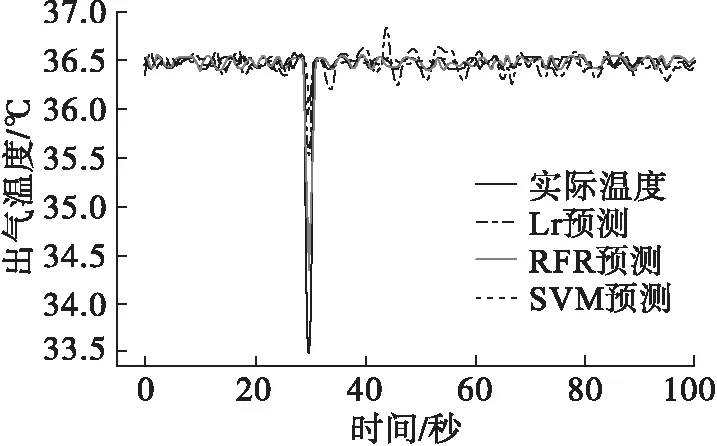
图8 10 L/min工况下出气温度预测对比图

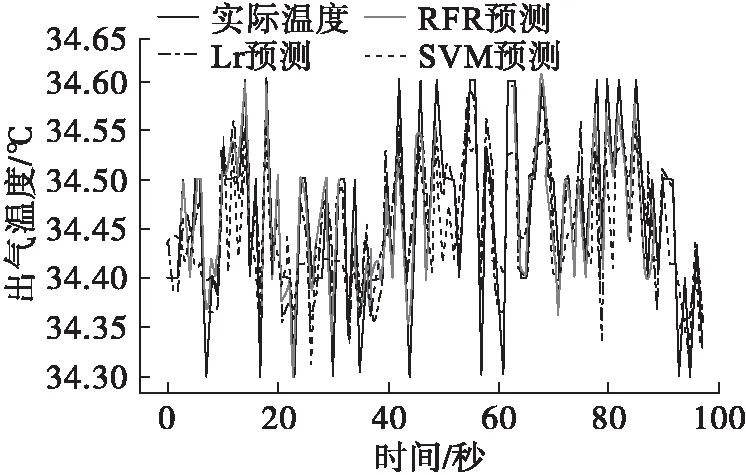
图9 10 L/min工况下出气温度预测对比图

为有效评价模型拟合效果，使用以下四个指标分析不同模型的预测准确性。

4.1 可解释方差

可解释方差(VS)作为一种评价指标[19]，主要用来解释自变量对因变量方差的解释程度，其计算公式如下：

(19)

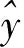
4.2 平均绝对误差

平均绝对误差(MAE)作为一种评价指标，主要用来说明预测结果和真实数据的接近程度，其值越小越好，其计算公式如下：

(20)

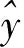
4.3 均方误差

均方误差(MSE)作为一种评价指标，主要表示拟合数据和原始数据的拟合程度，其值越小表示拟合效果越好，其计算公式如下：

(21)

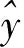
4.4 判定系数

判定系数R2的含义是解释回归模型的方差得分，取值范围为[0,1]。一般情况下，得分为0，代表模型拟合效果很差；得分为1，则代表模型很准确。但这种情况并不是绝对的，一般情况下样本数量的增加也会对R2产生影响，所以无法定量的说明准确程度，其计算公式如下：

(22)

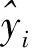
4.5 结果分析

该文选用了四种常见的评价指标，对模型的性能进行评价，相关参数如表2、表3所示。

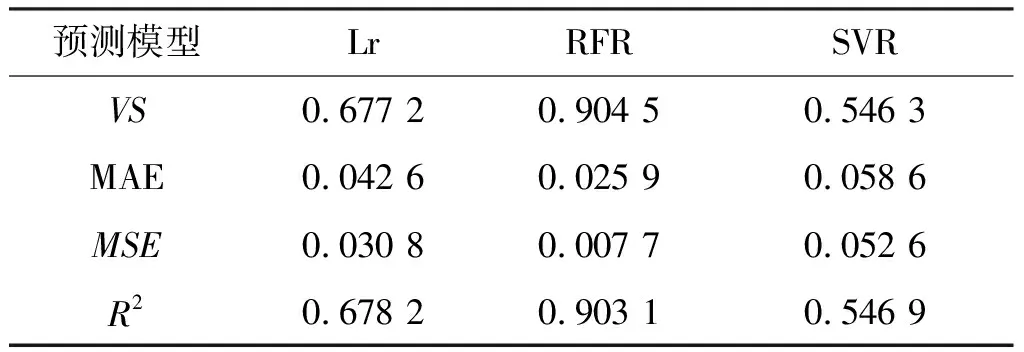
表2 37 ℃，10 L/min工况下各预测模型评估表

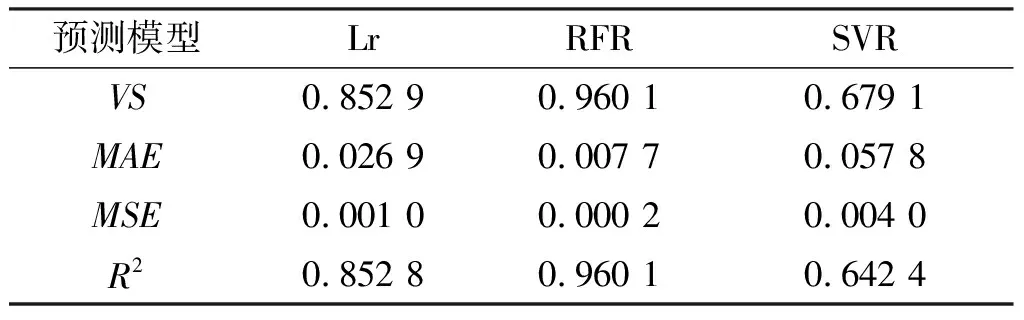
表3 37 ℃，80 L/min工况下各预测模型评估表

因此，从表2、表3可知，随机森林预测模型的拟合效果都是最优，多元线性回归的效果次之、支持向量机的效果最差。鉴于被控目标特殊性及复杂性方面的考虑，以及各种算法对数据集要求的不同，该结果也符合常归认知。但不难发现，三种模型皆可以对出气温度做出预测，符合预期。

5 结论

该实验是针对湿化治疗仪出气温度预测的研究，具有很强的实用性；同时，以生产企业真实数据为基础，使结果更具说服力。实验分别选用多元线性回归、随机森林和支持向量机三种算法分别进行数据建模。首先将数据集进行划分，其次是模型的训练及预测。从结果可以看出，在湿化仪出气温度预测问题中，随机森林预测模型的拟合效果都是最优的，多元线性回归的效果次之、支持向量机效果最差。但从预期效果来看，三种算法都可以对出气温度做出一定程度的预测，只是存在精度方面的差别。该实验结果只是基于特定样本情况下的对比分析，为了使预测结果更加准确，还需要做进一步探索。