EEMD-GSSA-SVM滚动轴承故障诊断方法研究*
2022-04-12宋立业
宋立业, 孙 琳
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
0 引 言
滚动轴承故障是旋转机械的各类故障中最容易发生的一种故障,而且一旦发生,将会严重影响整个机械的正常工作,因而对滚动轴承故障诊断技术的研究是非常重要[1~4]。相关研究人员针对滚动轴承故障诊断技术已经做了不少研究,应用较多的有反向传播(back propogation,BP)神经网络、支持向量机(support vector machine,SVM)以及专家诊断系统等[2],由于BP神经网络存在训练时间长、对样本数量要求大,以及易早熟收敛的问题,而专家诊断系统则存在运行维护困难以及建立所需时间长的问题,由此利用对样本数量要求不高以及非线性问题处理能力强的SVM进行故障诊断的研究越来越多。但单纯利用SVM对故障进行诊断,又存在需人工设置参数而导致自适应能力差以及诊断精度低的问题。对此相关研究人员提出使用优化算法对SVM参数进行选取[5,6],但利用现有的诸如粒子群优化(particle swarm optimization,PSO)等算法对SVM参数进行优化选择[7],又存在易早熟、选取精度低的问题。
针对上述问题,本文提出使用集合经验模态分解(ensemble empirical mode decomposition,EEMD)与能量矩对滚动轴承原始运行信号特征进行提取,然后利用全局麻雀搜索算法(global sparrow search algorithm,GSSA)对SVM参数进行优化选取,最后利用优化好的SVM对滚动轴承进行故障诊断的方法。本文利用实验对所提方法的有效性以及优越性进行了验证。
1 诊断信号特征提取
1.1 EEMD方法
EEMD是针对EMD方法所存在的模态混叠以及端点效应问题而提出的一种将频率分布均匀的高斯白噪声多次加入原始信号,而使原始信号极点特征得以改善的模态分解方法[8~10],这种算法在对信号进行模态分解时,自适应能力相对较强,因而更能对原始信号进行表征。
1.2 能量矩特征提取方法
能量矩是一种考虑了时间尺度的特征提取方法,因为考虑了时间尺度,所以相对单纯的能量特征提取方法更能表征原始信号。对于能量矩特征提取方法的具体过程如下:
按式(1)对EEMD得到的各IMF分量以及余量进行能量矩计算
Ej=∑(T·k)|cj(T·K)|2
(1)
式中Ej为第j个IMF分量的能量矩,T与k分别为采样周期与采样点标号。
按式(2)对特征向量进行构建
(2)
2 GSSA建模与验证分析
2.1 GSSA的建模
原始SSA是一种模拟麻雀群觅食过程的优化算法,该算法通过引入探索者、追随者以及预警机制,使其在求解精度和抗早熟等方面相对其他优化算法具有很大的优势。但原始SSA算法在探索粒子更新时,其搜索范围是随着迭代的进行而逐渐减小的,这种机制会严重影响算法的收敛速度,而且极有可能陷入局部解。针对这个问题,本文提出一种考虑全局最优位置的GSSA,对于GSSA的具体建模过程如下[11]:
对于M维、N个群体的GSSA,初始化其个体为Xi=(xi1…xii…xiM),此时,整个群体可表示为X=(X1…Xi…XN)。首先,种群中的探索粒子按式(3)进行更新
(3)
式中w为动态惯性因子,具体按式(4)进行更新;Q为服从标准正态分布的随机数;W为M维单位向量;预警因子ST取值范围为0.5~1。此时算法考虑了前一代最优位置的影响,使探索者粒子移向最优位置的速度加快,而不是原始SSA的盲目本地搜索,提升了算法的全局收敛速度;同时算法加入了动态权重因子,使得算法开始时受全局最优位置影响较大,从而加快算法收敛速度,而随着迭代的进行,这种影响逐渐减小,受算法本身预警机制的影响使算法不易陷入局部解。式(4)如下
(4)
种群中追随粒子按式(5)进行更新
(5)
其中,A+的计算方式为
A+=AT(AAT)-1
(6)
由式(6)可得出,当i>n/2时,表示此时位置极差,粒子需要跳出当前位置;反之,则追随探索粒子移动。
种群中随机预警粒子更新方式为
(7)
式中β为步长控制参数,k为服从-1~1之间的均匀随机分布的数,ε为避免分母为0而加设的极小数字。由式(7)可知,算法预警机制主要为防止算法陷入局部解而设置的,即当随机选中的粒子处于最佳位置时,表示其处于危险状态,须向其他位置移动。由上述GSSA的具体流程如下:
begin
初始化算法参数以及种群位置
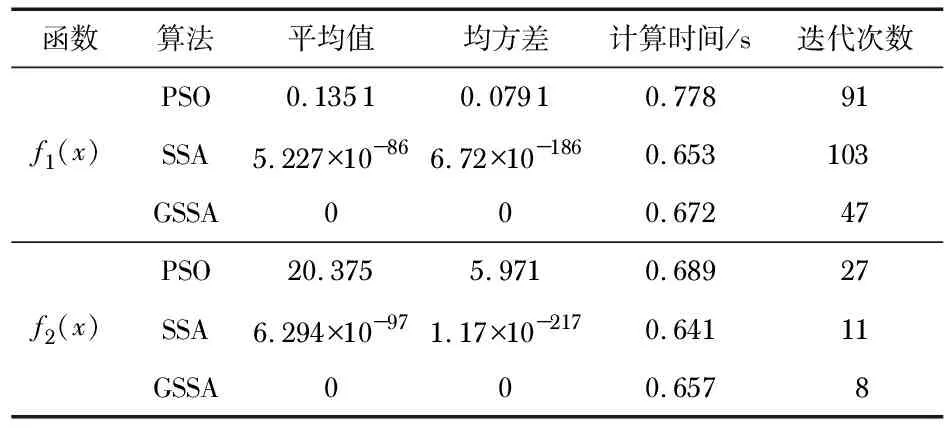
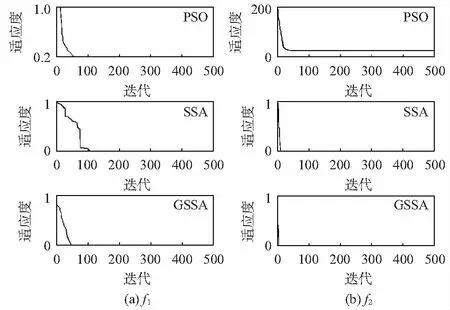
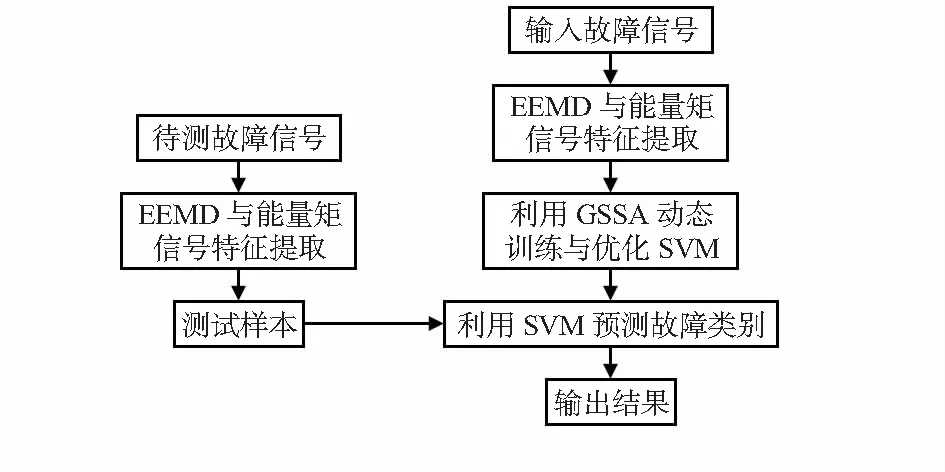
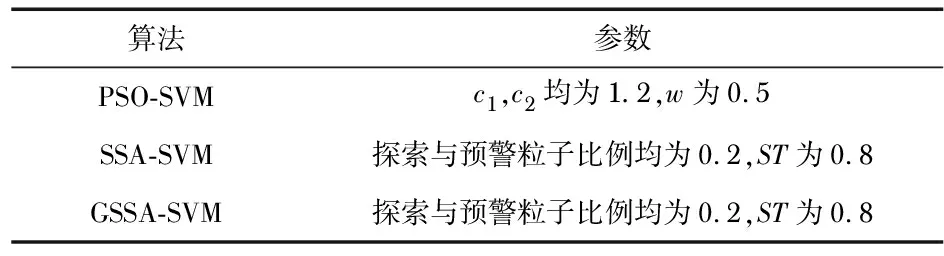
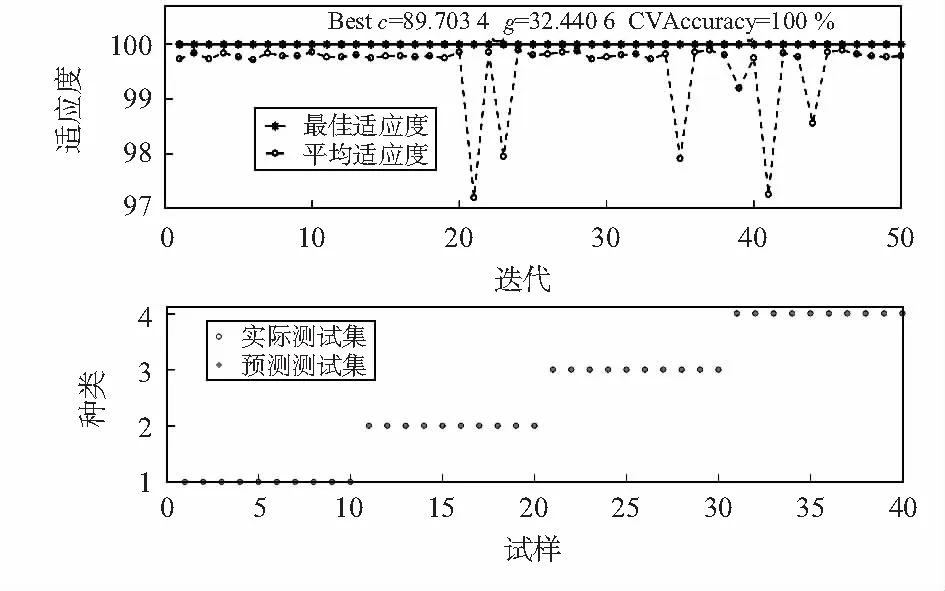
while (t 计算个体适应度,排序并寻找最优位置 按式(3)与式(4)更新探索粒子 对追随粒子按式(5)与式(6)进行更新 随机挑选预警粒子,并按式(7)进行更新 更新种群 t=t+1 end while end 为验证算法的有效性,分别利用PSO、SSA以及GSSA对如式(8)所示的一例单峰多维以及如式(9)所示一例多峰多维经典函数进行50次求解。两例函数的维数均为30维,且最优值均为0。式(8)、式(9)如下 (8) x∈[-5.12,5.12] (9) 对于算法参数设置为:探索与预警粒子比例均为0.2,ST为0.8,具体种群个数均为100,迭代500次。给出上述三种算法结算结果如表1所示,运行迭代结果如图1所示。 表1 计算结果 图1 迭代运行结果 由表1的结算结果可以看出,GSSA对于上述两式50次求解的平均值与均方差均为0,显示出所提算法无论是计算精度还是计算稳定性都相对其他两种算法高。另外由图2的迭代运行结果可以看出GSSA还具有求解收敛速度快的优势。 由于本文处理的信号为非线性信号样本,因而此时非线性SVM的预测函数[12,13]可用式(10)表示 (10) 式中air与br分别为利用部分样本预先利用式(11)求得的第i个样本的Langrange算子以及偏置因子 (11) (12) 式中K(xi,xj)为SVM核函数,本文选择的是径向基核函数,具体如式(12)所示;C为惩罚因子,表示的是算法的容差能力,越大则表示算法对训练结果的准确度越高;g为径向基宽度。 由此可以利用GSSA对C与g两个参数进行优化计算,来使得SVM算法在分类识别过程中的交叉验证结果最大。对于交叉验证方法本文选择的是K-CV法,其中k取值为5,即每5组数据选1组作为验证样本。由此基于EEMD-GSSA-SVM算法的滚动轴承故障诊断流程如图2所示。 图2 诊断流程图 为了验证本文所提方法的有效性,本文利用西储凯斯大学轴承检测中心所给数据,针对采样频率为12 kHz,转速为1 750 r/min,负荷大小为2HP以及损伤尺寸为0.007 in(1 in=2.54 cm)的滚动轴承。利用本文所提方法分别对其内圈、外圈、滚动体故障以及正常运行状态进行分类识别,对于具体实验平台如图3所示。 图3 振动信号采集平台 本文针对滚动轴承内圈、外圈、滚动体故障以及正常运行状态分别采集了80组数据,其中每组数据含有1 024个数据点,所以本文所采数据一共包含320组数据,每种类型数据共采集81 920个点。对每组数据首先利用EEMD法进行模态分解,然后对分解得到的IMF分量利用能量矩进行归一化的特征提取。 对于滚动轴承故障诊断分析,本文分别给出利用PSO-SVM,SSA-SVM以及GSSA-SVM算法对滚动轴承故障状态的分类识别结果,对于上述算法的参数设置具体如表2所示,此外,上述算法迭代次数均设置为50次,种群数为20。而对于所采集处理得到的数据,设置40组数据为测试集样本,剩下的280组数据为训练集样本。 表2 算法参数设置表 利用上述算法对滚动轴承故障分类识别进行50次计算,取平均计算后的识别结果如表3所示。由计算结果可以看出,本文所提算法能在几乎不改变原始算法复杂度的前提下,相对SSA-SVM算法识别交叉验证准确率提高了5.78 %,相对PSO-SVM算法识别交叉验证准确率更是提高了9.81 %,而且由于多次实验结果相同,验证了所提算法对于滚动轴承故障识别分析运算的稳定性。 表3 识别结果表 对于利用EEMD-GSSA-SVM对滚动轴承故障识别分析的迭代结果与识别结果如图4所示。 图4 迭代识别结果 为提高旋转机械滚动轴承故障诊断精度,本文提出了一种基于EEMD-GSSA-SVM算法的滚动轴承故障诊断方法。首先利用EEMD以及能量矩对原始信号进行了特征提取。然后提出了一种GSSA,即在SSA探索粒子更新过程中引入全局最优位置以及可变惯性因子,既加快了算法的收敛速度,又减小了算法陷入局部解的可能,并利用经典函数对其有效性以及优越性进行了验证。最后提出利用GSSA优化SVM中的C,g参数,然后利用GSSA-SVM算法对滚动轴承故障进行诊断,经实验验证,本文所提GSSA-SVM算法具有识别准确率高以及识别稳定度高的优势。2.2 GSSA的验证

3 GSSA-SVM算法建模

4 方法实验分析


5 结 论
