压缩感知理论在蝗灾监测中的应用*
2022-04-12熊晓婷许学杰李素文
熊晓婷, 许学杰, 李素文
(淮北师范大学 物理与电子信息学院,安徽 淮北 235000)
0 引 言
2020年1月份,非洲爆发了数十年来最大的蝗虫灾害,本次蝗灾具有虫群规模大、入侵面积广、蔓延速度快和破坏力强等特点,给当地的农业生产活动带来了巨大的损害,因此设计一套远程抗灾诊断系统,用于实时监测受灾现场、了解蝗虫迁徙和变异情况很有必要。为了及时掌握最新灾情,需要大量的蝗虫图像数据充实蝗虫图片库,这给系统的采集、存储和传输工作带了很大的压力,如何高倍率的压缩数据和高精度的重构图像对于远程监控农业病害领域具有重要意义。
压缩感知理论[1,2]是一种突破奈奎斯特采样定理的新理论,该理论以稀疏表示为前提条件,以测量矩阵为中间桥梁,以重构算法为关键技术,通过数量远小于传统理论所需的采样值即可实现信号的重建[3,4]。近些年,将压缩感知理论应用于监测农业病害的研究一直是热点。文献[5]提出了基于切换字典策略的压缩算法,在监测林区小气候时比单一字典算法的重构误差更小;文献[6]将基于K-SVD字典的压缩感知方法应用在林区微环境监测,比DFT字典具有更优的重构性能;文献[7]结合拟牛顿法和最速下降法的优点对光滑L0范数算法进行了改进,提高了SAR重构图像的分辨率;文献[8]根据余弦距离判别将相近的字典原子聚类,利用块结构字典重构信号,降低了重构误差。尽管这些研究针对某些局部问题进行了改进,但总体重构精度较低。基于此,本文首先构造新型观测矩阵,通过改善观测性能为后续重构打下良好的基础,接着针对CoSaMP算法选择原子和删除原子标准的局限性,提出一种基于参数u的改进算法,最后通过仿真对比实验验证了该算法的优越性。
1 算法描述
1.1 压缩感知理论
压缩感知理论指出,如果信号是稀疏的或者在某个变换域是稀疏的,则该信号可以通过与稀疏基不相关的观测矩阵从高维空间投影到低维空间,达到压缩的目的,若观测性能良好,低维信号应该包含原始信号足够的关键信息,此时可以通过求解一个最优化问题高概率恢复原始信号。由此可见,稀疏性、观测矩阵和重构算法是压缩感知的三个重要步骤。
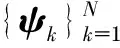
(1)
式中 若α仅有K个原子不为零或者绝对值明显大于其他原子,且K远小于N,则称x在该变换域上是稀疏的,即K为稀疏,ψ为稀疏基。
现实中要处理的大部分信号都不具备稀疏性,因此选择合适的稀疏基显得尤为重要。常用的稀疏基有离散傅里叶变换基、离散余弦变换基、离散小波变换基等,本文采用小波变换基作为稀疏基,因为小波基具有较好的能量聚集特性,能使信号的能量集中在少数小波系数上,从而达到稀疏的效果[9]。
2)观测矩阵。假设一个长度为N的K-稀疏离散信号x,该信号在观测基Φ上得到的观测结果为
y=Φx
(2)
式中Φ为观测矩阵,大小为M×N,y为观测值,大小为M×1,该值不破坏原始信号的关键信息,才能为后续的精确重构打下基础。观测矩阵分为随机型矩阵和确定型矩阵,随机型矩阵观测性能好但硬件实现难,确定型矩阵易于实现但观测性能较差,典型的观测矩阵有随机高斯矩阵、部分傅里叶矩阵、伯努利矩阵等[10,11]。
3)重构算法。得到M个观测值后,根据观测矩阵和重构算法实现信号的精确重构是压缩感知的最后一步,本质上是通过求解一系列优化问题实现对原始信号的精确重构。
重构算法主要分为两大类,1)凸优化算法,2)贪婪算法。凸优化算法计算复杂度大,重构时间长,贪婪算法则复杂度低,重构速度快,且精度较高,应用也最为广泛。常用的贪婪算法有:正交匹配追踪算法(OMP),正则化正交匹配追踪算法(ROMP),压缩采样匹配追踪算法(CoSaMP)等[12]。
1.2 改进的观测矩阵
在众多观测矩阵中,高斯随机观测矩阵因其极大的随机性,使得它和大多数信号的相关性都很低,所需的观测数偏小,但随机性强带来计算复杂、性能不稳定和硬件实现难等问题;部分哈达玛观测矩阵观测性能较好,但需要对行列进行取舍,应用范围有限;伯努利观测矩阵随机性较强,且较容易实现,但观测性能一般。本文结合多种观测矩阵的构造思想,在伯努利矩阵的基础上设计了一种新观测矩阵,取长补短,在保持原观测矩阵优点的同时进一步提高观测性能,设观测矩阵的尺寸为M×N,整个设计分为构造阶段和筛选阶段两部分,在筛选阶段,以相关性作为迭代的标准,根据前后两次观测矩阵相关性之差自适应更改步长,重新调整观测矩阵结构,若相关性小于一定阈值,则停止迭代。
相关性是衡量矩阵性能的一个重要准则[13],数学描述如下
(3)
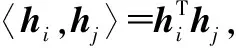
构造阶段:初始值i=1,μ0=0。
1)得到一个不大于观测矩阵行数的一半且是2的整数次幂的值k0,令过渡值k=k0-w0,其中w0为步长,初始值为0;
2)分别构造随机矩阵H0和伯努利矩阵H1,尺寸分别是(M-k)×k和M×(N-k);
3)构造元素仅有+1和-1的正交矩阵H2,尺寸为k×k;
4)将H0和H2组合成矩阵H3,尺寸为M×k;
5)将H3和H2组合成矩阵H,尺寸为M×N,即为暂时的新观测矩阵;
6)计算新观测矩阵的相关性μi。
筛选阶段:若μi小于阈值,停止迭代。若μi大于上一次迭代的μi-1,则正向调整步长w0,否则反向调整步长w0,返回步骤(1),自适应改变过渡值k,多次迭代得到相关性最低的观测矩阵即为最终的新观测矩阵。
1.3 改进的重构算法
在各种经典算法中,OMP算法是一种常用的贪婪算法,该算法收敛速度快且易实现,但鲁棒性差,在有噪声干扰时不能保证精确重构;ROMP算法采用正则化的思想对OMP算法进行了改进,重构效率高,但其每次迭代选择的原子会一直保留在候选集,可能导致错误累计,重构效果不稳定,而CoSaMP算法采用回溯的原则,前一次迭代选择的错误原子可能在下一次迭代中被剔除,从而提高了性能的稳定度,该算法的基本思想是:先选择2K(K为信号稀疏度)个原子,确保候选集中有至多3K个原子,再剔除至多2K个原子,留下的K个原子即为此次迭代得到的支撑集。该算法采用了回溯的思想保证每次迭代时选择原子的准确性,但在每次迭代中,选择与剔除原子所依据的标准不一样且具有一定局限性,即观测矩阵各列和残差的内积值并不能完全反映出二者之间的关系,完全依赖于它导致重构精确度受到偏坏的影响,基于此,本文提出了一种改进的算法:uCoSaMP算法,在原子选择阶段,引进修正因子u,它反比于观测矩阵各列与残差的差值的二范数,利用它自适应地修正残差与观测矩阵各列的相关性,提高初选原子候选集的正确率;在原子剔除阶段,分为两步:先采用最小二乘法将候选集尺寸缩小到2K,再利用信号和残差的加权值获得最终的支撑集,使得选择和剔除原子的标准趋同,具体的算法流程如下:
输入:传感矩阵A,观测向量y,稀疏度K,参数u。
初始化:r0=y,Δ0=∅,A0=∅,t=1。
1)计算v=uATrt-1,u为相关于观测矩阵原子和残差的参数,选择v中2K项最大的元素,这些元素对应的列序号q构成集合Q0,即q∈Q0;
2)合并Δt=Δt∪Q0,At=At∪aq;

6)更新rt=y-Atktk;
7)计算前后两次迭代残差差值的二范数‖rt-rt-1‖2,若超过一定阈值,则修正参数u,并返回步骤(1),否则At中对应的列记为Atk=Atk′,对应A的列序号记为Δtk=Δtk′,At=Δtk,并返回步骤(1);
8)若‖rt‖2小于一定阈值,则终止迭代,否则继续迭代。
2 试验分析与比较
2.1 评估标准
对于两幅质量差别较大的图像,人眼能够直观地辨别出图像质量的好坏,若人眼较难辨别时,可以采用峰值信噪比PSNR作为评估指标,它是基于图像重建前后原子均方误差的度量标准,表示为
(4)
式中max为图像数据的峰值,MSE为均方误差,定义为
(5)
式中M×N为图像的尺寸,A(i,j)和B(i,j)为图像重构前后的数据。
2.2 实验结果
2.2.1 基于不同观测矩阵的实验结果
本实验中,测试图像分别选用纹理和细节丰富的近景蝗虫和远景蝗虫图像,稀疏基采用小波稀疏基,重构算法采用CoSaMP算法,观测矩阵分别采用高斯(Gaussian)随机观测矩阵、伯努利(Bernoulli)观测矩阵和新(New)观测矩阵,比较三种观测矩阵在各采样率(M/N)下的实验结果如表1所示。
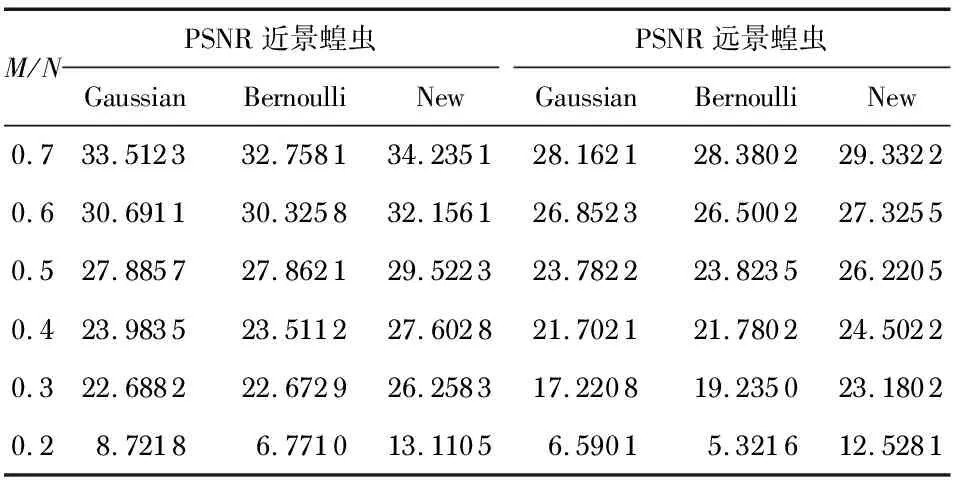
表1 基于不同观测矩阵的重构性能比较 dB
从表1可以看出,新观测矩阵的观测性能具有较大的优势,即重构后的输出信噪比高于高斯随机观测矩阵和伯努利观测矩阵,当压缩比下降时,优势则进一步增大,当压缩比达到0.5时,高斯随机观测矩阵和伯努利观测矩阵的观测性能开始恶化,而新观测矩阵依然保持较好的观测性能,当压缩比达到0.2时,三者的观测性能都急剧下降,因为此时的观测值中已经丢失了较多原始信号的关键信息。图1和图2分别给出了蝗虫近景原图和蝗虫远景原图及其在采样率为0.5时不同观测矩阵下的重构结果,从图中可以很直观地看出,新观测矩阵的重构图像质量较高,重构图的纹理清晰平滑,线条连续,而另外两种矩阵的重构图像质量较低,颗粒较多。综合表1、图1和图2,要达到相同的重构效果,新观测矩阵的压缩比可以相对减小,所需存储的数据更少,抗噪声性能更强。

图1 蝗虫近景图和基于不同观测矩阵的重构图像(M/N=0.5)

图2 蝗虫远景图和基于不同观测矩阵的重构图像(M/N=0.5)
2.2.2 基于不同重构算法的实验结果
本文实验先采用小波稀疏基作稀疏处理,再采用新观测矩阵进行观测降维,最后采用原始CoSaMP算法和本文提出的uCoSaMP算法分别对近景蝗虫和远景蝗虫图像进行重构,比较两种算法在各采样率(M/N)下的实验结果如表2所示。
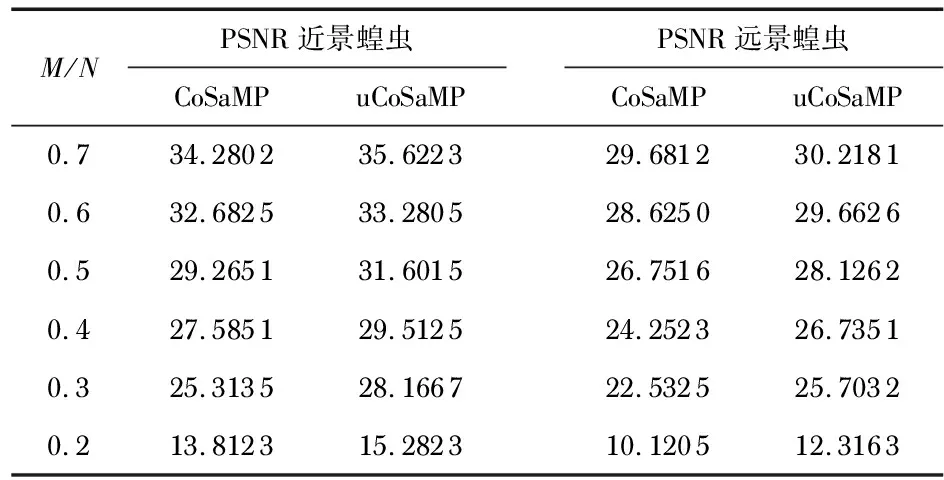
表2 基于不同重构算法的重构性能比较 dB
从表2可以看出,两种算法都能成功重构原始图像,但uCoSaMP重建图像的PSNR值明显高于原始算法,当压缩比为0.6以上时,这种优势并不突出,但随着压缩比的减小,PSNR值越来越小,重构性能差距反而有增大的趋势,当采样率达到0.2时,近景图峰值信噪比提高了10 %。图3、图4和图5、图6分别给出了蝗虫近景和远景原图在采样率为0.5和0.3时,基于不同重构算法的重构图像,从图中可以直观对比出两种算法的优劣:当采样率较高时,两种算法重构的图像质量均较优,蝗虫和周边环境的重要特征均得到良好的保持,细节区域没有出现明显模糊的现象;当采样率较低时,两种重构图像均出现了不同程度的恶化,但uCoSaMP重建图像的颗粒状现象和模糊程度要弱一些,整体的图像质量高于CoSaMP算法,这也说明了改进算法的鲁棒性更强。

图3 蝗虫近景原图和基于不同重构算法的重构图像(M/N=0.5)

图4 蝗虫远景原图和基于不同重构算法的重构图像(M/N=0.5)

图5 蝗虫近景原图和基于不同重构算法的重构图像(M/N=0.3)

图6 蝗虫远景原图和基于不同重构算法的重构图像(M/N=0.3)
3 结 论
本文将压缩感知理论应用到蝗虫灾害监测中,首先根据随机观测矩阵和伯努利观测矩阵的特点构造新观测矩阵,通过新观测矩阵降维得到的观测值具备更优的重构潜能,然后引进修正因子,自适应修正残差和备选原子间的相关性,通过改良初选原子标准提高原子候选集的准确度,在剔除原子阶段分两步逐一淘汰错误原子,使得最终的支撑集得到进一步的优化。实验结果表明:改进算法重构蝗虫图像的质量更高,在低采样率下,近景蝗虫图像相比于原始算法提高了10 %,且改进算法的鲁棒性更强,在监控农业病害领域具有良好的应用价值。自然图像一般不具备稀疏特质,而稀疏性对重构性能的影响较大,因此如何进一步有效地稀疏化图像是接下来研究的重点。
