基于虚拟阻抗的并网逆变器前馈控制策略研究*

黄玉和，郑寿森，何来沛

中山大学物理学院，广东 广州 510275

分布式发电技术的研究对新能源技术的发展具有重要推动作用，而并网逆变器作为组成分布式发电系统的重要设备也成为了研究热点，其中并网电流的质量是其关键指标［1-2］。并网逆变器采用的正弦脉宽调制（SPWM）技术会产生大量由功率器件动作引起的谐波，需采用L型或者LCL 型滤波器来保证输出电流的质量。相较于使用L型滤波的并网逆变器，LCL型逆变器对高次谐波有着更好的抑制作用，同时还能以较小的电感获得与L型滤波器使用大电感时同等的滤波能力，有效地降低了并网逆变器的体积和成本［3］。但LCL 滤波器是一个三阶的无阻尼系统，它的使用会为逆变器系统引入谐振峰，造成系统的不稳定，为了获得稳定的并网电流控制效果，研究者提出许多控制方案。

按照控制对象的不同，这些方案可分为直接电流控制和间接电流控制［1］，直接电流控制因为LCL滤波器引入的谐振峰的存在，需要采取额外的措施来保证系统的稳定性。如文献［4-5］通过串联谐波滤波器的方式实现与系统谐振频率的零极点对消，但该方案对系统的控制精度具有很高的要求且难以兼顾系统的带宽、相位和幅值裕度。间接电流控制如逆变器侧电感电流反馈法［6］和分裂电容法［7］均只需使用单环反馈就能实现系统的稳定且都提出了应对电网质量下降的方案，但因为他们的被控对象都不是并网电流，所以使用该法的并网逆变器往往存在输出电流波形失真和功率因素不高等问题。从增加系统阻尼来抑制LCL谐振峰的角度，这些方法可以分为无源阻尼法和有源阻尼法两种［1］，值得一提的是，无源阻尼和有源阻尼方案均属于直接电流控制。无源阻尼法在LCL 滤波器的电容或电感支路通过串联或并联电阻的方式对LCL 滤波器固有的谐振峰进行抑制，这种方法易于实现且系统鲁棒性高，但会增加额外的功率损耗［8］。有源阻尼法则是通过将滤波器中的电容或者逆变器侧电感的电压值或电流值反馈到系统中实现系统的鲁棒性控制，该法不会产生能量损耗，但需要增加一个传感器采集电路的电流或电压［3］。文献［9］提出并总结了基于虚拟阻抗的有源阻尼方案，此法原理是通过将并网电流的二次微分项反馈到系统中以实现在滤波电容两端并联电阻的效果，无需增加额外的传感器即可实现对LCL 谐振峰的抑制，而引入并网电流的二次微分项放大了电网电压对并网电流的负面影响，使其电流总谐波畸变率增大。

针对基于虚拟阻抗的有源阻尼方案抗干扰能力不足的问题，本文在文献［9］的基础上，对系统的结构进行解耦，分析电网电压对输出的并网电流的影响，并以此为根据采用电网电压完全前馈的控制方法对该逆变器系统做出改进，通过在二次微分项上串联二阶低通滤波器的方式对电网电压和并网电流的二次微分项进行等效替代。该方案无需额外的传感器，降低了逆变器的成本，并且消除了电网电压对并网电流的影响，具有高功率因数的优点。在Matlab/Simulink 上的仿真结果证明了该方案能达到预期的效果。

1 基于虚拟阻抗的并网逆变器系统

Gd表示系统的总延时，可以看作一个采样周期的计算延时和相当于半个采样周期的零阶保持器延时的叠加，因此可以表示为

其中Ts表示采样周期。

在图2 中，Gcom表示延时补偿器，在采用有源阻尼的逆变器系统中，系统延时是一个不可忽视的条件。系统延时的存在会改变系统的相频特性，从而影响系统的稳定性，严重限制了控制带宽，特别当谐振频率出现在高于采样频率的1/6 的区域时，在单位圆外存在一对极点，使系统无法保持稳定［11-12］。本文采用文献［12］中基于等面积法的补偿器来抵消系统延时的影响，其传递函数为

图1 单相LCL并网逆变器电路图Fig.1 Circuit diagram of single-phase LCL grid-connected inverter

图2 基于虚拟阻抗的并网逆变器传递函数框图Fig.2 Block diagram of virtual impedance based grid-connected inverter′s transfer function

当m= 0.8 时，该补偿器可完全抵消系统延时给并网逆变器系统带来的影响。

在系统延时得到充分补偿后，接下来对系统的分析中便可将串联补偿器的延时环节看作一个增益为1 的比例环节。同时将从i2引出的有源阻尼的反馈节点后移，获得如图3所示的简化框图。

图3 简化后的并网逆变器传递函数框图Fig.3 Simplified grid-connected inverter′s transfer function diagram

在图3 中，Gieq为引入有源阻尼后从逆变器输出电压uinv到并网电流i2的等效传递函数，从图中可以推导出

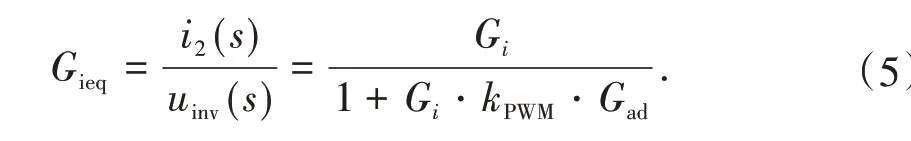
由文献［9］可知，通过如图4 所示的方法，在LCL 滤波器的电容两侧并联虚拟阻抗Rv可以得到使用有源阻尼控制器Gad时的等效电路。据此，可以得到此时由逆变器输出电压uinv到并网电流i2的传递函数式为

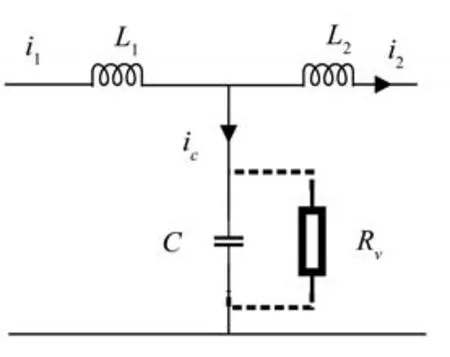
图4 在滤波电容两侧并联虚拟阻抗Rv时的等效电路图Fig.4 Equivalent circuit diagram when Rv is connected in parallel with the filter capacitor

2 电网电压前馈控制策略

从图5（c）中可以看出，当公共接入段电压VPCC进入电流控制环路后，经Gx2后对并网电流i2产生影响，为了完全消除可能携带电网扰动的VPCC对逆变器输出电流的负面作用，需要增加一条前馈回路对电网电压进行补偿［6，13］，其控制结构如图6（a）所示。同时，为了更好地实施控制方案，结合实际电路结构，得到如图6（b）所示的前馈方案。

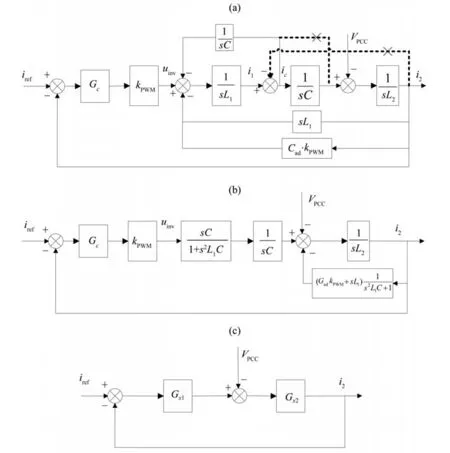
图5 系统等效变换过程Fig.5 Equivalent transformation of the system

根据图6（b），该电压前馈回路包含一个比例项和一个二次微分项，其中二次微分项在转化为差分方程后包含超前项，不易于数字实现，且易受高频谐波干扰。为了克服这一问题，本文通过串联二阶低通滤波器在低频段实现对二次微分项的等效替代。串联该低通滤波器的二次微分环节的传递函数为

图6 带电压前馈的系统控制图Fig.6 Diagram of inverter system with voltage feedforward

一般情况下，当ζ= 0.707，ωs取LCL 滤波器谐振频率的4～5 倍时，Gs2eq能取得较好的等效结果［9］，注意到当ωs= 40 000 rad/s 时，b2= 0，此时的ωs满足上述条件，且能减少一次乘法和一次加法运算，提高程序运行效率。通过伯德图验证了上述方法能达到设计要求。值得一提的是，Gs2eq同时适用于对电压前馈回路和有源阻尼回路中的二次微分项s2的等效替代。

3 系统参数整定

按照上文的设计步骤，得到并网逆变器系统的整体控制方案如图7所示。

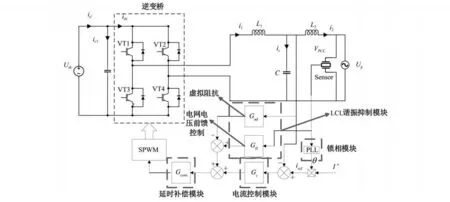
图7 LCL型并网逆变器控制结构图Fig.7 Control structure of grid-connected inverter system with LCL filter

图7 中的Gff为前馈控制器，其表达式由图6（b）得出，即

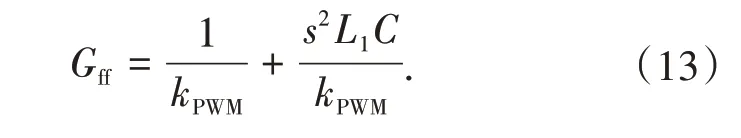
对比图3和图6（b）可知，在采用完全电压前馈控制前后，电流环路的前向通路的各个模块并没有发生改变，故系统的增益也保持不变，前馈控制的加入消除了电网电压对并网电流的影响，在电流环的参数整定过程中只需要考虑电流环路自身的各项性能即可完成对系统参数的整定。采用有源阻尼控制方案的LCL 并网逆变器的设计步骤一般为：先整定内环参数，再完成外环电流控制器的整定。

3.1 系统内环参数整定

调节内环参数是为了抑制LCL 滤波器的谐振峰。由公式（6）可以得出，对谐振峰的抑制效果取决于虚拟阻抗Rv的取值。为研究不同的Rv对系统的影响，得出虚拟阻抗Rv取不同值时Gieq的伯德图如图8 所示。从图8 可以看出，逆变器系统引入不同阻值的虚拟阻抗后，谐振峰均得到了一定的抑制。且随着Rv的减小，虚拟阻抗对系统的阻尼效果越明显。但Rv的值并非越小越好，过小的Rv会使系统的截止频率减小、带宽不足，从而导致系统的不稳定；而当Rv的值过大时，又会导致系统因欠阻尼而产生震荡，故Rv的阻值需要根据系统的实际需求折衷选取。经过实验研究，Rv=10 Ω满足本文提出的逆变器系统的设计要求。

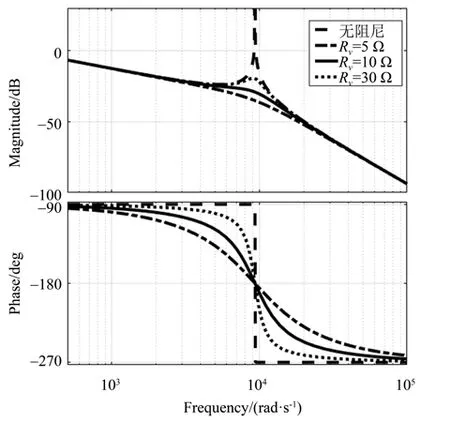
图8 Gieq的伯德图Fig.8 Bode diagram of Gieq

3.2 系统外环参数整定

为实现对电网工频信号的无静差跟踪，本文选用准谐振控制器对并网电流进行控制，该控制器引入的谐振角频率能有选择地放大系统工频信号处的增益，同时还增大了控制带宽，有效减小了频率波动对系统增益的影响［14］。该控制器的传递函数为

4 实验结果

本文设计了一台额定功率为2.2 kW 的单相并网逆变器，参照以上设计步骤完成了系统各个控制参数的整定，在表1 中列出了本文设计的单相LCL 并网逆变器的相关参数。依据图7 的系统结构和表1 的系统参数，在Matlab/Simulink 平台上搭建基于虚拟阻抗的并网逆变器完全电压前馈控制系统。本文通过对该方案的抗干扰能力、动态性能和稳态性能三个指标进行对比分析，验证了提出的前馈控制方案的有效性。

图9 逆变器系统的开环传递函数伯德图Fig.9 Bode diagram of inverter system

表1 系统参数Table 1 System parameter

4.1 抗干扰能力

本文将不使用前馈控制的控制方案作为对照组，并分别向两组系统注入5 次和11 次谐波，检测此时逆变器输出的并网电流的电流畸变情况，实验结果证明本文提出的逆变器系统具有良好的抗干扰能力。

图10 和图11 分别是向电网电压中注入5 次谐波和11 次谐波时采用不同前馈方案的系统输出的仿真波形。其中，5次谐波和11次谐波的幅值和相位分别为5%和0。从图中可以看出，使用完全电压前馈控制的系统输出在电网电压含有低次或者高次谐波的情况下均能保持完美的正弦波形，而不采用前馈控制的输出波形则产生了明显的失真。使用Simulink 中的FFT Analysis 工具分别计算使用完全电压前馈控制和不带前馈控制的系统输出的并网电流i2的THD，在电网电压含有5 次谐波分量时，得到两组的THD 分别为2.34%、6.40%；而含有11 次谐波分量时，得到两组的THD 分别为2.14%、5.02%。实验结果表明，当电网电压中含有谐波时，完全电压前馈控制策略可以消除电压畸变对逆变器输出电流的影响，对逆变器的稳定运行具有重要意义。

图10 当电网电压含有5次谐波时i2的波形Fig.10 Experimental waveform of i2 when the grid voltage contains the 5th harmonic

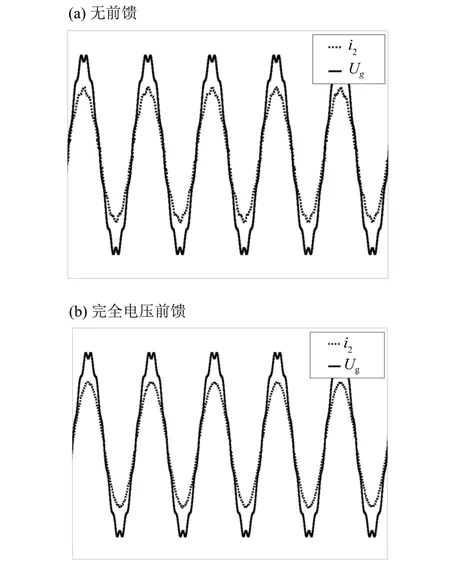
图11 当电网电压含有11次谐波时i2的波形Fig.11 Experimental waveform of i2 when the grid voltage contains the 11th harmonic

4.2 动态性能

图12 和图13 分别为电网电压幅值变化和逆变器负载变化时，完全电压前馈控制方案的输出波形。在图12中的1和2节点，使电网的电压幅值分别突变为正常运行时的80%和120%。从图中可以看出，在电网电压的幅值变化后，逆变器的输出电流能在半个周期内重新达到稳态，且电流的波形只在幅值变化瞬间产生了少许震荡。在图13中，逆变器系统的负载在1节点处从满载变为半载，而在2节点处又从半载变回满载，显然在负载变化发生后，逆变器能迅速地调节系统的输出，使之达到新的稳态，且在调节过程中系统的超调量很小。

图12 电网电压幅值变化Fig.12 Waveform of i2 when the grid voltage changes

图13 逆变器负载变化Fig.13 Waveform of i2 when the load changes

4.3 稳态性能

本文将电容电流反馈有源阻尼的控制方案［3，13］（方案一）和分裂电容法［7］（方案二）作为对照组，对比分析当系统稳定时，各个系统的误差电流波形。实验结果证明了本文提出的控制方案（方案三）稳态性能。

图14 为方案一到方案三稳定运行时并网电流i2和误差电流ie的波形，其中误差电流ie=iref-i2。表2则列出了各个逆变器设计方案所使用的传感器数量和稳定运行时并网电流的THD。从上述图表中可以看出，三种控制方案均满足并网逆变器入网电流的THD＜5%的要求［1］，其中方案二的并网电流的波形则出现了轻微的变形，同时其误差电流的峰值超过2 A 且呈明显的工频周期波动，而电容电流反馈的控制方案（方案一）和基于虚拟阻抗的控制方案（方案三）的误差电流ie都不超过0.5 A，证明两者的电流控制效果均优于分裂电容法（方案二），验证了本文所用控制方案具有良好的稳态性能。而在控制精度相同的情况下，方案三无需额外的传感器即可完成对逆变器系统的信息采集，降低了逆变器的制造成本，比方案一更具有吸引力。

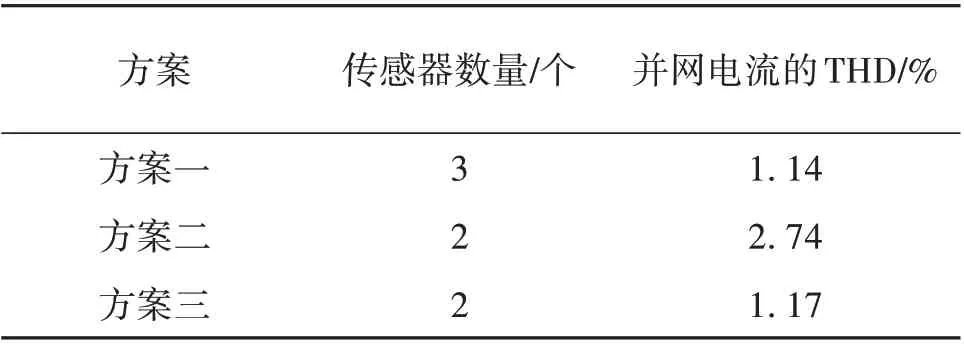
表2 各个方案的传感器数量和并网电流的THDTable 2 Number of sensors and THD of grid-connected current in each cases

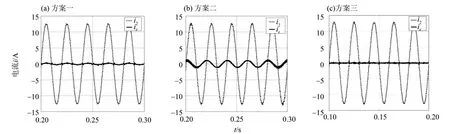
图14 稳定运行时各方案并网电流i2和误差电流ie的波形Fig.14 Waveforms of grid-connected current i2 and error current of ie of each case in steady state

5 结 论

本文分析了基于虚拟阻抗的逆变器的系统结构，推导了适用于该系统的完全电压前馈控制策略以改进其易受电网电压波动影响的不足，并完成了延时补偿模块、谐振抑制模块和电流控制模块的设计。采用这种控制方案的逆变器系统无需使用额外的传感器，降低了制造成本，且因该系统外环采用的是直接电流控制，保留了电网电流跟踪性能良好、并网功率因数高的优点。2.2 kW并网逆变器的实验结果显示，引入完全电压前馈后，逆变器对电网电压中的谐波具有很好的抑制作用，在逆变器系统的抗干扰能力、动态性能和稳态性能三个关键指标方面均有良好的表现。特别在电网电压中含有谐波的场合，该前馈控制方案对比无前馈控制方案具有明显的优势。