电阻抗成像探测地下溶洞的几种方法*
2022-04-12吴泽宇刘祚秋汪利
吴泽宇,刘祚秋,汪利
中山大学航空航天学院,广东 广州 510006
电阻抗成像方法是可以用于探测地下溶洞的一种方法,其原理是根据物体内部不同物质的导电参数(如电阻率、电容率)的不同,通过对物体表面电流、电压的施加和测量来获知物体内部导电参数的分布,进而重建出反映物体内部结构的图像,该方法的难点一是固有的病态性,即边界电压数据的微小扰动可能引起解的巨大变化;另一个困难是它的信息量小。如何实现系统的高精度、高分辨率和算法的快速收敛是其应用的主要难点[1]。
电阻抗成像的起源可以追溯到20 世纪20 年代,地球物理学研究者提出了线性电极阵列的电阻率成像(Resistivity Imaging)技术。19 世纪70年代,生物医学研究者提出了圆形电极阵列的断层电阻率测量技术(Tomographic Resistivity Measurement Technique)。1978 年,Henderson 和Webster 做出了第一幅电阻抗图像。他们使用固定于胸部上的由一大电极和与之相对的若干小电极组成的电极系统。通过测量从各小电极流向大电极的电流所形成的等位差,获得了可以清楚地显示肺脏位置的阻抗图像。但是这还不是断层图像,而是类似X 胸片的透视图像。1982 年,英国Sheffield大学的Brown 和Barber 实现了第一个手臂的阻抗层析图像,开辟了电阻抗层析成像(EIT)技术这一新的研究领域[2]。
本文采用电阻抗成像法探测了地下溶洞,并采用Tikhonov正则化和稀疏正则化方法以解决反问题固有的非适定性问题;在正则化的过程中运用了灵敏度分析法,又分别采用线性近似直接求解和迭代求解两种方法进行求解,并进一步分析了几种方法的识别精度与误差敏感度,为实际工程中的地下溶洞识别提供了一定的参考。
1 问题的描述
1.1 正问题
考虑一个空间区域Ω 及其边界∂Ω[3-4],电阻抗成像的正问题是在已知材料电阻抗率ρ(x),x∈Ω(或其倒数,视电阻率c(x) = 1/ρ(x))的情况下,求解区域内的电势u(x)(或电压)分布。考虑边界∂Ω上输入输出电流,正问题的控制方程[5]为
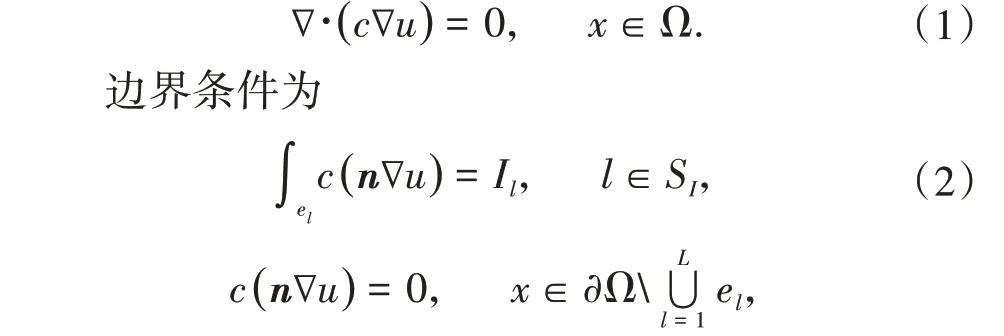
其中n为边界上的外法向向量,SI为所有边界电流点(或电极)的集合,考虑电流几乎为单点输入输出,el表示的是包含电流点l的微小区域,Il是点l处的电流量。Il>0 表示电流输入,Il<0 则为电流输出。如果某个电极方案只有点1 输入单位电流,而点2 输出单位电流,则有I1= 1,I2= -1,Il=0,l∈SI{1,2}。此外,还可以测量一系列边界点的电势,这些测量的电势点的集合记为Su;电势点Su与电流点SI可以有部分重合。问题(1)~(2)是典型的Neumann 边值问题,为了确保解的存在性,需要满足所有输入输出电流总和为0,即
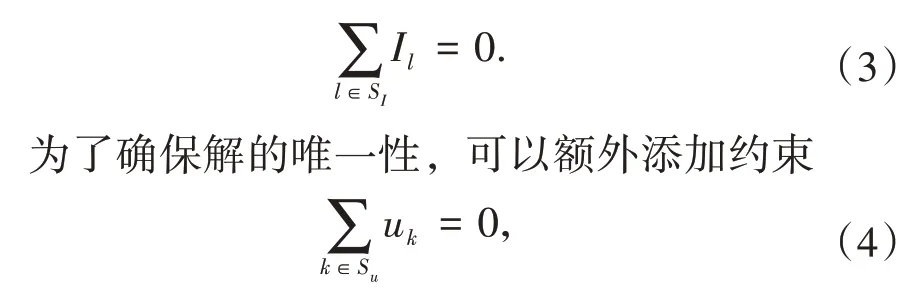
其中uk表示点k上的电势。
基于以上描述,考虑电阻抗成像探测地下溶洞这一问题(如图1 所示)。问题所属区域简化为图1右侧的矩形区域。电流点与电势点不一致,但数目相等。
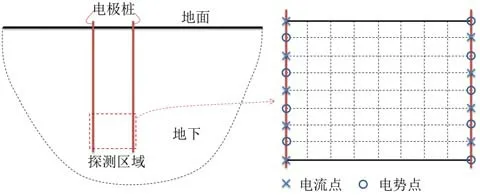
图1 电阻抗成像探测地下溶洞示意图Fig.1 Diagram of electrical impedance imaging for cavity detection
通常可以使用有限元进行正问题求解,得到如下方程

其中Kj为单位电阻率时的单元刚度矩阵。
1.2 反问题

2 电阻抗成像的理论与方法

2.1 初值或平均视电阻率估计

此时,可以选择初值为c0=c01。
2.2 灵敏度分析

接下来,将根据已有的初值c0和灵敏度矩阵进行参数识别。考虑使用不同的正则化方法(Tikhonov 正则化[8]和稀疏正则化[9])以及是否迭代的因素,主要可以分为4 种方法:Tikhonov 更新法、稀疏更新法、Tikhonov迭代法、稀疏迭代法。
2.3 Tikhonov更新法
这里假设初值c0与待识别结果c比较接近,此时可以对R(c)使用Taylor展开,得到

其中正则化稀疏λ>0 可通过L-curve 方法[10-11]进行确定。
2.4 稀疏更新法
同样考虑如公式(12)~(13)的线性近似的过程,但使用稀疏正则化处理非适定性。实际溶洞探测问题中,溶洞的存在相对于探测区域通常体积较小,在空间分布上具有一定稀疏性(或更新量(c-c0)是稀疏的),因此可以使用稀疏正则化进行处理。稀疏更新法的求解问题为

2.5 Tikhonov迭代法


2.6 稀疏迭代法
与Tikhonov迭代法类似,稀疏迭代法则表现为使用稀疏更新法重复、迭代求解的过程。迭代式为

3 数值算例
选取矩形区域长宽均为4 m×4 m,每边均匀划分为8 个单元,假设初始区域的视电阻率是均匀的,取值为c0= 10。考虑如图2 中三种溶洞情况(溶洞处的视电阻率等效为3,相对于土体的10,有较大的折减),其中Case 1、Case 2 为单个溶洞的情况、Case 3为多个溶洞的情况,图块颜色与视电阻率的对应关系如图右侧色标所示。
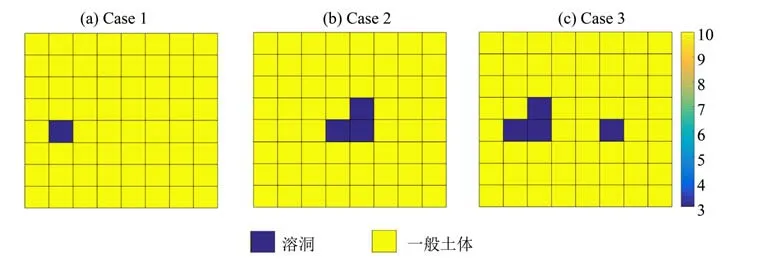
图2 溶洞探测的三种情况Fig.2 Three cases of cavity detection
考虑如图1右侧的矩形区域和电极方案,通过给定的电流与真实视电阻率分布得到电势结果,分别利用Tikhonov 更新法、稀疏更新法、Tikhonov迭代法和稀疏迭代法识别以上三种溶洞情况。其中Tikhonov 法的正则化参数通过L-curve 方法进行确定,而稀疏正则化参数取10-8。
另外,考虑误差存在时的情形,此时电势情况u=u0(1+ fr·Randn);其中,u0为真实电势;Randn是与电势矩阵同阶的随机数矩阵,其每个元素都是[-1,1]上的正态分布随机变量;fr为变量的系数,这里取fr = 0.001。
Case 1在无误差和有误差情况下的识别结果分别如图3~4 所示,Case 2 在无误差和有误差情况下的识别结果分别如图5~6 所示,Case 3 在无误差和有误差情况下的识别结果分别如图7~8所示。从结果中可以看出:

图3 无误差时Case 1的识别结果Fig.3 Results of Case 1 without error
1)Tikhonov 更新法在无误差的情况下识别单个溶洞(图3 和图5)时,在溶洞位置可以识别到视电阻率的折减,但与真实情况相比,视电阻率在数值上相差较大,结果较为粗糙;而在有误差的情况下(图4和图6),在溶洞位置也能看出视电阻率的差别,但与无误差情况相比,结果的差别较大;而在识别多个溶洞的情况时(图7 和图8),无论是否有误差,视电阻率的分布较为混乱,多处出现电阻率折减,电阻率在数值上与真实情况有较大差别,无法识别出正确的溶洞位置。

图4 有误差时Case 1的识别结果Fig.4 Results of Case 1 with error
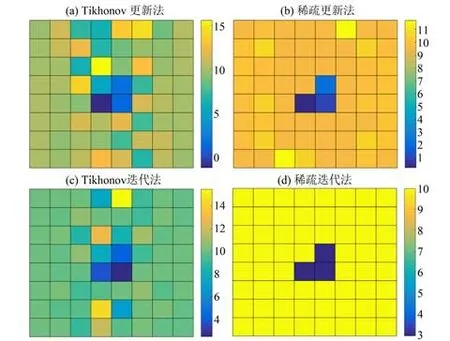
图5 无误差时Case 2的识别结果Fig.5 Results of Case 2 without error

图6 有误差时Case 2的识别结果Fig.6 Results of Case 2 with error
2)稀疏更新法在无误差的情况下识别单个溶洞(图3 到图6)时,可以明显地看到溶洞位置有明显的视电阻率折减,而在其他位置的视电阻率在数值上与真实情况十分接近;识别相邻的多个溶洞的情况时(图7和图8),较大溶洞处有视电阻率的折减,但不能完全识别出溶洞形状,数值上也与真实情况有较大差别;且较小溶洞处没有视电阻率的折减,其他位置的视电阻率也与真实情况有一定差别,但各处视电阻率之间相差不大,且无误差和有误差结果相似。

图7 无误差时Case 3的识别结果Fig.7 Results of Case 3 without error

图8 有误差时Case 3的识别结果Fig.8 Results of Case 3 with error
3) Tikhonov 迭代法在无误差的情况下识别单个溶洞(图3 和图5)时,在溶洞位置可以识别到视电阻率的折减,其他位置的视电阻率与真实情况在数值上存在较大差别,且视电阻率分布不均匀。在有误差的情况下(图4和图6),视电阻率分布混乱,有多处位置存在明显的视电阻率折减,无法识别出溶洞位置;而在无误差的情况下识别多个溶洞时(图7),能准确识别到溶洞位置处的视电阻率折减,其他位置的视电阻率也较为均匀。但在有误差的情况下(图8),整个识别区域的视电阻率分布混乱,无法识别到溶洞位置。
4) 稀疏迭代法溶洞探测效果非常好,在无误差的情况下识别单个与多个溶洞(图3、图5 和图7)时,结果与真实情况几乎完全一致;而在有误差的情况下(图4、图6 和图8),结果也基本保持不变。
4 结 论
Tikhonov 更新法方法简单,可以大体识别单个溶洞的位置,但结果粗糙,对误差较为敏感,且无法识别相邻的多个溶洞;稀疏更新法也比较简单,识别单个溶洞时结果较好,对误差敏感度也较低,但在识别相邻的多个溶洞时存在遗漏;Tikhonov 迭代法比Tikhonov 更新法复杂,在无误差时能识别单个或多个溶洞的位置,但对误差的敏感程度非常大,在有误差情况下完全无法识别出溶洞位置;稀疏迭代法计算量大,但识别结果非常好,对误差的敏感度也很低,无论是否有误差,无论是识别单个还是多个溶洞,都能得到非常理想的结果。
总而言之,从结果上看,几种方法的排序(由好到坏)为:稀疏迭代法>稀疏更新法>Tikhonov更新法>Tikhonov迭代法。
