连续刚构拱组合桥拱脚等效静力刚度研究*
2022-04-12康俊涛邹立连岳泉
康俊涛,邹立,连岳泉
武汉理工大学土木工程与建筑学院,湖北 武汉 430070
连续刚构拱组合桥的拱脚是拱肋和主梁的关键连接部分,通常受力复杂且局部边界条件难以确定[1]。在全桥计算分析中,拱脚单元的刚度对全桥内力状态有显著影响。目前已有部分学者对以上问题进行了研究分析:曾亚能等[2]引入拱脚等效静力刚度概念及计算方法,对系杆拱桥拱脚等效静力刚度展开研究,得到系杆拱桥拱脚合理等效静力刚度;周萌等[3]提出了适用于系杆拱桥拱脚的多尺度有限元建模方法,能较好地模拟结构复杂边界条件;关伟等[4]对下承式梁拱组合连续梁桥拱脚进行空间应力分析,得出了梁拱结合段在活载作用下的应力分布特点;欧阳辉来等[5]对下承式钢箱系杆拱桥的拱脚结构进行了详细分析,为类似桥梁拱脚结构设计提供了指导。除上述外,还有大量学者对拱脚连接处进行了研究[6-8]。目前,拱脚刚度的研究偏少,且主要集中于系杆拱桥。由于系杆拱桥拱脚附近主梁截面位移可忽略,截面边界条件考虑为固结[9],而连续刚构拱组合桥通常采用悬臂浇筑施工,主梁两侧位移不可忽略(需考虑内力相互作用)。所以,其拱脚等效静力刚度需进一步研究确定。
针对连续刚构拱组合桥的特点,本文对连续刚构拱组合桥的拱脚静力刚度进行了分析,通过对比不同刚度的拱脚局部梁单元模型与拱脚局部实体单元模型中拱肋位移的差值,得到了适用于连续刚构拱组合桥的拱脚等效静力刚度系数,最后对比分析了全桥梁单元模型(不考虑拱脚静力等效刚度)、全桥梁单元模型(考虑拱脚等效静力刚度)两种模型结构的受力状态。
1 拱脚等效静力刚度
1.1 基本理论
由于拱脚刚度的取值对连续刚构拱组合桥的全桥计算具有显著影响,拱脚若采用拱肋梁单元一致刚度模拟,则计算得到的全桥内力状态并不足够精确。采用如下步骤得到合理拱脚等效静力刚度[2]:第一步,建立拱脚局部杆系模型和拱脚局部实体模型,提取全桥模型中拱肋截面内力和主梁截面内力,并在两个模型上施加完全相同的弯矩、剪力和轴力,计算拱脚实体模型及拱脚局部杆系模型中的拱肋位移;第二步,改变拱脚局部杆系模型中的拱脚单元的截面刚度调整系数(即改变了拱脚静力刚度),可得到与拱脚实体模型计算的拱肋位移最接近的系数k,则此时的k即为连续刚构拱组合桥的拱脚合理等效静力刚度。
1.2 模型要点
依据圣维南原理,0#块的应力状态与其附近结构的应力分布关系密切[10-12]。结合连续刚构拱组合桥的结构及施工特点,取主梁0#块、1#块、2#块、拱座、主拱肋及桥墩按照实际构造建立局部实体有限元模型,在桥墩底部施加固端约束,在主梁和拱肋截断位置的截面质心作用指定的弯矩、剪力和轴力。同样,建立等效的梁单元拱脚局部模型,桥墩底部固定约束,拱脚位置单元采用与附近拱肋相同截面,拱脚与主梁采用刚性连接,施加与实体模型相同的节点荷载。
2 工程实例概况
福厦铁路江坑内大桥为跨径组合(76+160+76) m 的预应力混凝土连续刚构拱组合桥。桥梁全长313.6 m,全宽14.2 m,中跨跨中及边支点梁高3.0 m,中支点梁高8.5 m。拱计算跨径160 m,拱轴线为抛物线,上、下拱肋设计失高分别为31.4 m 和29.5 m,拱脚段一定区域内上下钢管用缀板联结成哑铃型截面,拱肋上下弦管采用直径为120 mm 的钢管,内填C55 自密实补偿收缩混凝土。吊杆顺桥向间距8 m,全桥共设18 组双吊杆,吊杆上端锚于上拱肋上缘张拉底座,下端锚于吊点横梁下缘固定底座。桥型布置示意图如图1所示。

图1 江坑内大桥桥型布置图(单位:cm)Fig.1 Bridge-type layout of Jiangkengnei Bridge(unit:cm)
3 数值分析
3.1 评定方法
为得到连续刚构拱组合桥的拱脚合理等效静力刚度,可根据拱肋位移差值与局部实体模型位移的比值作为拱脚等效刚度系数的评定指标,二者比值最小时,即为连续刚构拱组合桥拱脚单元等效静力刚度k,按式(1)计算。

式中γk为拱脚等效静力刚度评定指标,Sk为拱脚刚度系数为k时拱肋位移值,Ssol为局部实体模型中拱肋位移值。
由于拱脚模型在荷载作用下,拱肋横桥向位移与顺桥向位移、竖向位移相比较小,在此忽略不计,计算拱肋节点顺桥向位移和竖向位移即可。所以,式(1)转化为

式中Sh、Sv 分别表示梁单元模型和实体模型中拱肋顺桥向、竖向位移值。
对于实体或杆系有限元模型,均由节点组成,则应该计算对应节点的顺桥向及竖向位移差值,然后计算各差值的平均值,则可得到拱肋不同位置的位移响应曲线,按式(3)计算
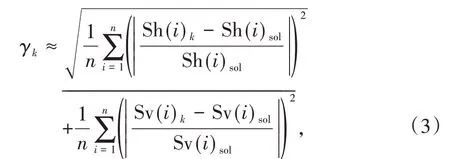
式中n表示拱脚有限元模型节点数量,Sh(i)k、Sv(i)k分别为刚度系数取k时杆系单元第i号节点纵桥向位移和竖向位移,Sh(i)sol、Sv(i)sol为拱脚实体模型第i号节点顺桥向位移和竖向位移。
当γk值取最小值时,所对应的等效刚度系数则为基于拱肋位移的合理等效刚度系数,此时杆系模型中拱脚的刚度即为所求的拱脚单元合理静力刚度。
3.2 有限元模型
3.2.1 全桥有限元模型采用Midas Civil 建立江坑内大桥全桥有限元模型,全桥离散为1 028 个节点,1 124 个单元,吊杆采用桁架单元,其余均采用梁单元,江坑内大桥有限元模型如图2所示。

图2 Midas Civil有限元模型Fig.2 Finite element model of Midas Civil
3.2.2 局部有限元模型采用Midas Civil 建立拱脚局部杆系模型,主梁(0#、1#、2#块)、拱肋及桥墩均采用梁单元建立,其中主梁与桥墩、主梁与拱脚均采用刚性连接,在主梁端截面及上下拱肋截面施加指定大小的外力,墩底固端约束;拱脚局部实体模型采用Midas FEA 建立,除钢管采用板单元建立外,其余均由实体单元建立,在截面形心质点位置施加与杆系局部模型相同的外荷载和边界条件。拱脚杆系模型及拱脚实体模型如图3-4所示。

图3 拱脚杆系模型Fig.3 Truss model of arch foot
图4 拱脚实体模型Fig.4 Entity model of arch foot
3.3 荷载取值
在全桥有限元模型中,提取结构在主力组合下主梁两侧截面内力、上钢管拱肋截面内力及下钢管拱肋截面内力,如表1所示。

表1 主梁及拱肋截面内力Table1 Internal force of main bean and arch rib section
4 计算分析
对拱脚局部杆系模型和拱脚局部实体模型进行静力计算分析。调整拱脚局部杆系模型中拱脚单元的刚度调整系数k,k取值依次为1、10、15、20、25、30、40、50,得到拱脚局部模型中拱肋在不同刚度调整系数k下不同位置的顺桥向和竖向位移值,其中哑铃型截面计为截面形心处位移值,部分上、下钢管拱肋截面计为截面形心处位移平均值。
4.1 拱肋位移
拱脚局部实体模型在指定荷载作用下与拱脚局部杆系模型在初始刚度(刚度调整系数k=1)下的拱肋在不同位置的顺桥向位移如图5所示,调整拱脚局部杆系模型中的拱脚截面刚度系数k值后拱肋顺桥向位移如图6所示。

图5 实体模型与初始杆系模型的拱肋顺桥向位移Fig.5 Along-bridge displacement of arch ribs based on entity model and initial frame model
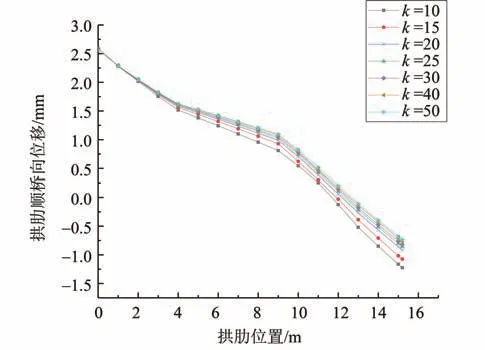
图6 不同拱脚刚度对应的拱肋顺桥向位移Fig.6 Along-bridge displacement of arch ribs based on different stiffness of arch foot
拱脚局部实体模型在指定荷载作用下与拱脚局部杆系模型在初始刚度(刚度调整系数k=1)下的拱肋在不同位置的竖向位移如图7所示,调整拱脚局部杆系模型中的拱脚截面刚度系数k值后拱肋竖向位移如图8所示。

图7 实体模型与初始杆系模型的拱肋竖向位移Fig.7 Vertical displacement of arch ribs based on entity model and initial frame model

图8 不同拱脚刚度对应的拱肋竖向位移Fig.8 Vertical displacement of arch ribs based on different stiffness of arch foot
4.2 拱肋刚度等效系数
对比不同刚度系数k时拱脚杆系模型中的拱肋的位移值与拱脚实体模型在相同荷载下的拱肋节点位移值,得到该桥拱脚静力刚度的评定指标,当评定指标γk取值最小时所对应的刚度系数k即为该桥合理的静力刚度系数,此时的拱脚刚度为拱脚合理静力刚度。不同刚度系数k对应的评定指标γk值如图9所示。

图9 拱脚等效静力刚度指标Fig.9 Index of the equivalent static stiffness of arch foot
由图9 可知,该桥拱脚合理静力刚度系数k位于15~25 之间时,评定指标取较小值,此时拱脚局部杆系模型中拱肋位移与拱脚局部实体模型中的拱肋位移最接近。所以,此时的拱脚刚度为拱脚合理等效静力刚度。
5 效应分析
根据上述分析,得到了江坑内大桥的拱脚合理静力刚度。为了研究拱脚刚度对全桥受力性能的影响,对比二组模型在主力组合下的成桥吊杆力及上下拱肋挠度变化。模型①为全桥杆系模型(拱脚与拱肋一致刚度),模型②为全桥杆系模型(拱脚考虑k=20的刚度调整系数)。
5.1 成桥吊杆力
全桥共18 组吊杆,考虑到结构对称性,取拱脚侧到中跨跨中的1-9#吊杆组进行分析,每组有4 根吊杆,以4 根吊杆在最不利主力的组合下成桥吊杆力的平均值作为该组吊杆的成桥吊杆力。在相同条件下,两组模型的成桥吊杆力如图10所示。
由图10 可知,江坑内大桥在考虑拱脚等效刚度系数后,靠近拱脚侧1-5#吊杆的成桥吊杆力均有一定程度减小,且1#吊杆成桥吊杆力减小最为显著,由421.3 kN 减小为386.0 kN,而靠近中跨跨中的成桥吊杆力有一定增大,但效应不明显。
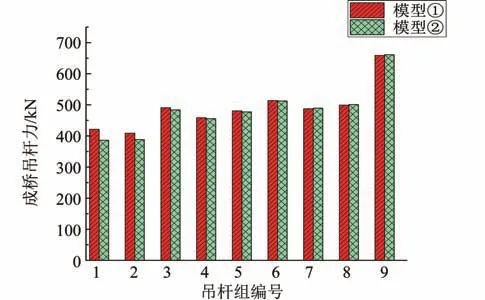
图10 成桥吊杆力Fig 10 Suspender force of bridge
5.2 拱肋挠度
两组模型在主力组合下的上、下拱肋成桥状态下挠度如图11-12所示。

图11 上拱肋位移Fig.11 Displacement of upper arch rib
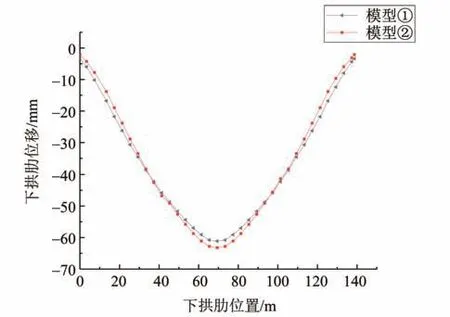
图12 下拱肋位移Fig.12 Displacement of lower arch rib
由图11-12可知,在考虑刚度调整系数后,连续刚构拱组合桥的上、下拱肋挠度在0~1/4L(拱肋跨度L)范围内呈现减小的趋势,而在1/4L~1/2L内为增大趋势,即考虑拱脚刚度调整系数后,连续刚构拱组合桥的上、下拱肋挠度在0~1/4L范围内计算值偏不安全,而在1/4L~1/2L内计算值偏保守。
6 结 论
本文以福厦铁路江坑内大桥为工程背景,对连续刚构拱组合桥拱脚单元合理静力刚度进行了研究,结论如下:
1)通过拱脚局部实体模型与拱脚杆系模型的位移响应的对比分析,得到江坑内大桥的拱脚合理静力刚度系数k为15~25;
2)在考虑拱脚合理静力刚度系数的情况下,靠近拱脚附近吊杆的成桥吊杆力明显减小,最大达35.3 kN,而靠近中跨跨中附近成桥吊杆力呈增大趋势,但效应不显著;
3)在考虑拱脚合理静力刚度系数的情况下,江坑内大桥上、下拱肋挠度计算结果在0~1/4L(拱肋跨度L)范围内呈减小趋势,表明拱肋挠度计算偏不安全,而在1/4L~1/2L内为增大趋势,表明拱肋挠度计算偏保守。
