基于Mooney-Rivlin模型的高水头伸缩式水封非线性仿真

2022-04-12胡坚柯陈吉丰汪振宁胡葆文郝楠楠胡梦溪

中国农村水利水电 2022年4期

胡坚柯，陈吉丰，汪振宁，胡葆文，王珏，郝楠楠，蔡锟，胡梦溪

（1.中国电建集团华东勘测设计研究院有限公司，杭州311122；2.河海大学机电工程学院，常州213022）

随着我国水利水电事业的不断发展，高压大流量水电站的建设也越来越多［1］。闸门作为水电站的核心部分之一，其止水可靠性问题也越来越突出。水封是闸门止水的核心装置，其结构性能是影响闸门止水能力的关键因素。闸门水封种类繁多，按照其结构的不同可以分为预压式水封以及伸缩式水封［2］，对于高水头闸门而言，由于传统的预压式水封需要过大的预压量而易导致止水元件在工作中磨损严重，寿命降低，因此高水头闸门多采用伸缩式水封作为止水装置［3-4］。

闸门止水装置在设计不当的情况下容易产生漏水的问题，恶化闸门的工作条件，甚至造成闸门的破坏。此外，高水头闸门止水装置一旦投入使用，检修以及更换都比较困难。因此，对伸缩式水封性能的研究就显得尤为重要。目前对水封性能的研究主要采用模型试验方法与数值仿真方法［5-6］，其中数值仿真方法是对不同工况下不同断面水封的工作情况进行仿真，从而确定水封的工作性能。数值仿真方法不受试验条件的限制，灵活性强，适用范围广。因此，数值仿真方法作为传统试验方法的补充在当前对水封性能的研究中被广泛的采用［7］。

水封由橡胶制成，橡胶具有大变形、不可压缩等特点，是典型的超弹性材料［8］。在对水封的仿真分析中，选用合理的材料本构模型用以准确地描述水封材料的应力-应变关系是保证模型分析精度的关键环节。对超弹性材料力学性能的描述方法主要分为两大类［9］，一类是基于连续介质力学的唯象理论，典型的有以Mooney-Rivlin（M-R）模型为代表的多项式模型；另一类是基于分子结构及构象熵改变的统计理论，典型的有Arruda-Boyce模型等。其中M-R模型能够很好地描述橡胶材料在中等应变情况下的应力-应变关系且形式简单、适用性强，因此，该类模型被广泛地应用在橡胶材料的非线性计算中［10，11］。根据参数数量的不同，M-R 模型可以分为二参数、三参数、五参数、九参数四种。低阶参数M-R 模型的公式简短、参数个数少，计算效率高且易收敛，但是随着模型参数的减少，对材料应力-应变关系的拟合精度也会有所下降。因此，在工程实例中，需要综合考虑所需计算精度以及计算效率从而选择最合适的本构模型。

在水封仿真领域内，当前国内已有较多的研究。薛小香等［12］对高水头P 型水封进行了非线性有限元模拟，得到了该类水封止水性能随预压缩量、封头几何尺寸变换的规律；熊威等［13］对山型水封进行了仿真，并比较了两种不同材质水封的止水性能。但以上的研究均缺乏对不同本构模型适用性的比较。刘礼华等［14］分析了不同参数M-R 模型在方形水封仿真中的适用性；谭显文等［15］研究了不同本构模型在不同试验数据、应变范围等条件下的适用性。但目前不同参数M-R 模型本构对高水头伸缩式水封的仿真精度影响还不明确，不同高水头工况对水封接触应力及变形的影响也有待进一步探究。因此，本文首先对不同参数M-R 模型在伸缩式水封数值分析中的精度进行了分析，从计算精度及效率的角度选择了合理的本构模型用于后续仿真。随后，本文对水封的自由外伸量、接触应力以及外偏移量在不同工作阶段的随水封所受背压、库压等因素影响而变化的规律进行了探究，为该类水封的设计提供了重要依据。

1 水封材料超弹性本构

基于连续介质力学的唯象理论假设橡胶是各向同性材料，用单位体积的应变能来表征其力学行为［16］，应变能对应变分量的导数就是相应的应力分量。应变能W的多项式表达如下［17］：

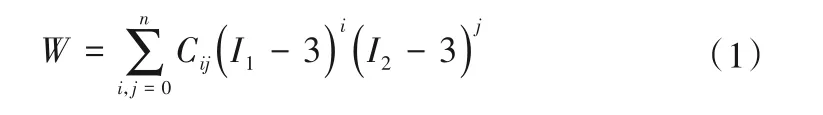
式中：n是多项式的阶数；Cij是材料系数；I1，I2都与主伸长率λ1，λ2和λ3有关，。

式中的n取不同的值对应的就是不同的多项式模型，就MR模型而言，各参数模型对应的应变能表达式分别如下。

二参数M-R模型：

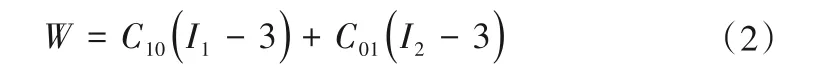
三参数M-R模型：

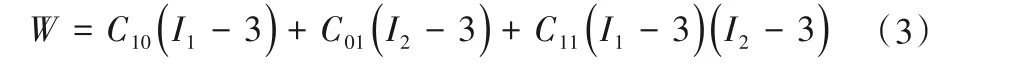
五参数M-R模型：

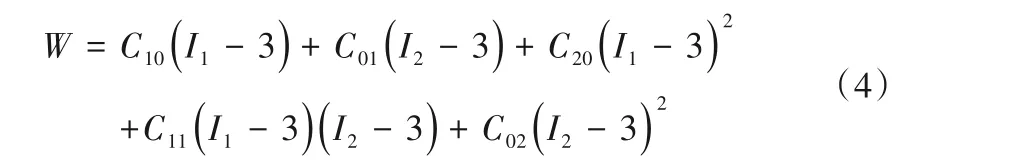
九参数M-R模型：

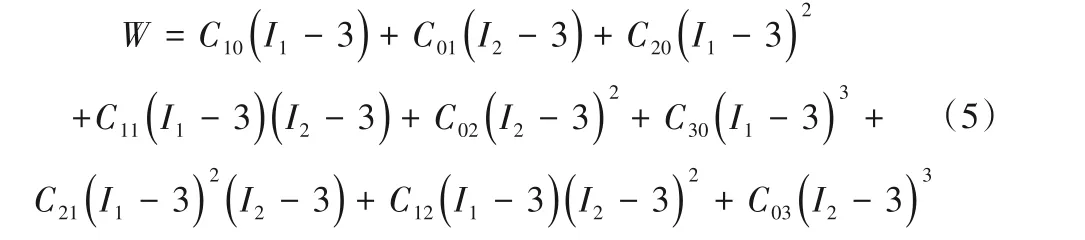
水封在工作时的荷载情况及应力状态比较复杂，为了较为全面的预测水封的应力应变特性，通常通过试验考察水封材料单轴拉压以及纯剪切三种应力状态，得到材料的应力应变数据以进行本构模型参数的计算。

2 有限元仿真

伸缩式水封止水装置主要由山型水封、止水面板、压板以及水封座板四部分构成。其中水封由橡胶制成，其余部分均为钢制。水封在工作过程中主要受到库压及背压的作用。止水装置具体结构如图1所示。

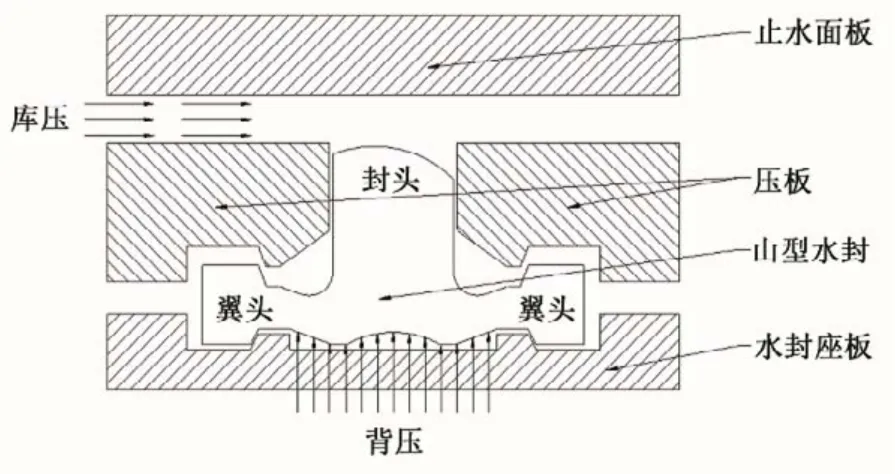
图1 伸缩式水封结构示意图Fig.1 Schematic diagram of expansion water seal structure

2.1 单元的选择

闸门水封的轴向尺寸远大于切向尺寸且水封所受荷载均平行于横截面作用，沿轴向保持不变，故闸门水封的仿真属于典型的平面应变问题。本文选用PLANE183单元建立水封止水装置的有限元模型。ANSYS 软件通过设置接触对实现物体的接触，本文使用CONTAC172- TARGE169 接触对单元，根据水封实际工作情况，在水封封头与止水面板之间、水封两侧及翼头与压板之间以及水封底部与水封座板之间分别设置接触对。经过上述工作，最终得到伸缩式水封止水装置的有限元模型如图2所示。

图2 止水装置有限元模型Fig.2 Finite element model of water stop device

2.2 约束与荷载

伸缩式水封止水的工作过程主要分为三步，对应的仿真分析过程也分为三个荷载步：

第一步，水封座板固定，两侧压板下压与水封座板共同挤压水封翼头，完成水封的安装。

第二步，对水封背部施加压力荷载（背压），同时止水面板向下位移至与压板上表面达到指定初始间隙。水封封头在背压作用下伸出与止水面板接触，完成水封的预压缩。

第三步：对水封迎水侧未有效接触部分施加库水压力。由于预压缩前水封与止水面板间接触状态未知，因此，需要首先进行荷载步一、二的仿真，并根据仿真结果确定库压施加范围。此外，施加库压后水封的受载发生变化，导致变形情况及接触状态同施加库压前不一致。因此，需要根据此时水封新的变形及接触情况重新施加荷载进行仿真并不断循环此过程，直至水封变形及接触状态趋于稳定。本文通过APDL语言中的循环与判断指令实现上述过程，具体命令如下。

DO，I，1，1000！开始循环

NSEL，S，，，180

*SET，K，1

*SET，L，K

*DO，J，160，206，2

！设置接触状态判断区域（迎水侧表面）

*GET，STOT，NODE，J，CONT，STOT

！提取施加库压后节点接触应力

*IF，STOT，LE，2000000，THEN

！判断施加库压后节点接触状态

NSEL，A，，，J，J+1

！收集未能有效接触节点

*SET，K，K+1

*ENDIF

*ENDDO

*IF，L，EQ，K，THEN

！判断施加库压后接触状态是否发生变化

*EXIT！没有变化，结束循环

*ENDIF

/PREP7！发生变化重新仿真

SF，ALL，PRES，P

！对此时未有效接触区域施加库压

ALLSEL，ALL

LSWRITE，3，

/SOLU

LSSOLVE，1，3，1，！计算

*ENDDO！结束循环

2.3 特征参数

在伸缩式水封的仿真分析中，主要采用以下特征参数衡量水封止水性能。

接触应力：水封封头与止水面板间由挤压而产生的，用于衡量水封能否有效止水。

接触宽度：水封封头与止水面板间接触区域的宽度，用于衡量水封止水的可靠性。

外偏移量：库压作用下水封封头右侧偏出右压板左端线的最大距离，该值过大不利于撤去背压后水封的复原且易降低水封寿命。

3 不同参数的M-R模型的比选

3.1 M-R模型参数拟合

本文基于水封橡胶材料的单轴拉压及纯剪切试验数据［14］，进行材料超弹性参数的拟合。针对M-R模型，基于最小二乘法原理分别对其二参数、三参数、五参数以及九参数模型进行了拟合分析，得到的各本构模型参数如表1所示，拟合曲线如图3和图4所示。

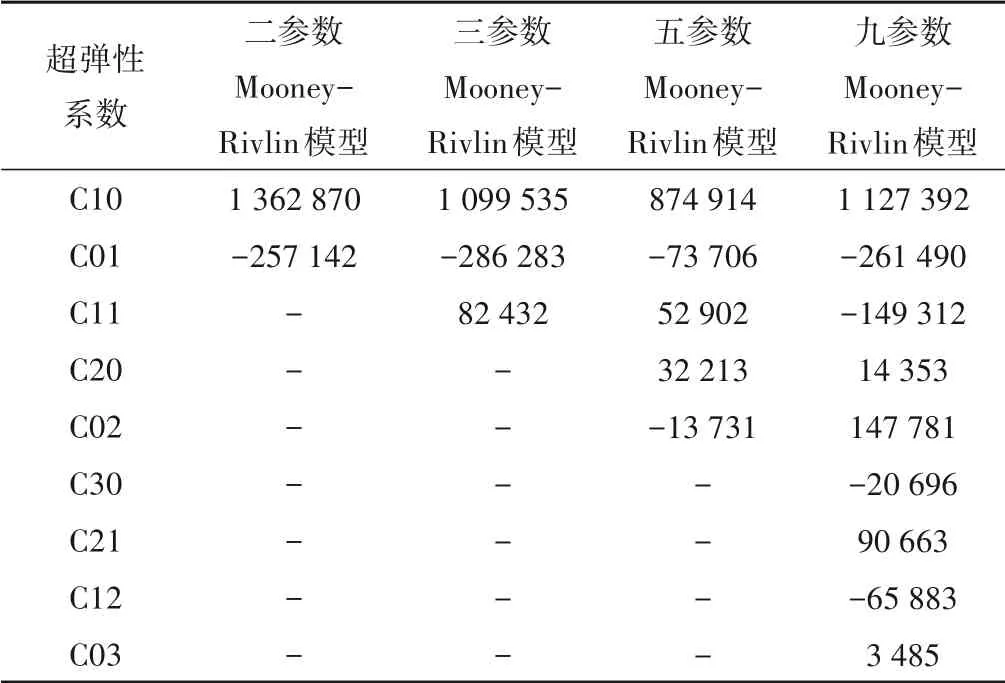
表1 高水头水封橡胶本构模型系数Tab.1 Coefficient of constitutive model of high water head water seal rubber

图3和图4表明：基于相同材料试验数据，不同参数M-R模型的拟合精度有所不同，且拟合精度随着模型阶数的增加而提升，从而可以在仿真计算中更真实的反应出水封在止水过程中的力学性能及变形特性。

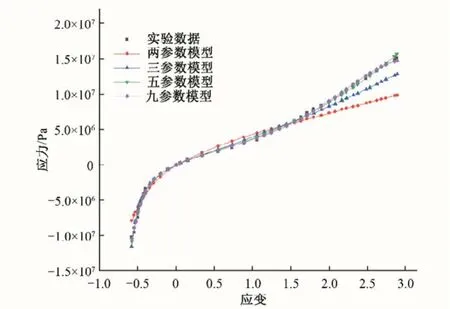
图3 单轴拉压试验拟合曲线Fig.3 Uniaxial tension and compression experiment curve fitting

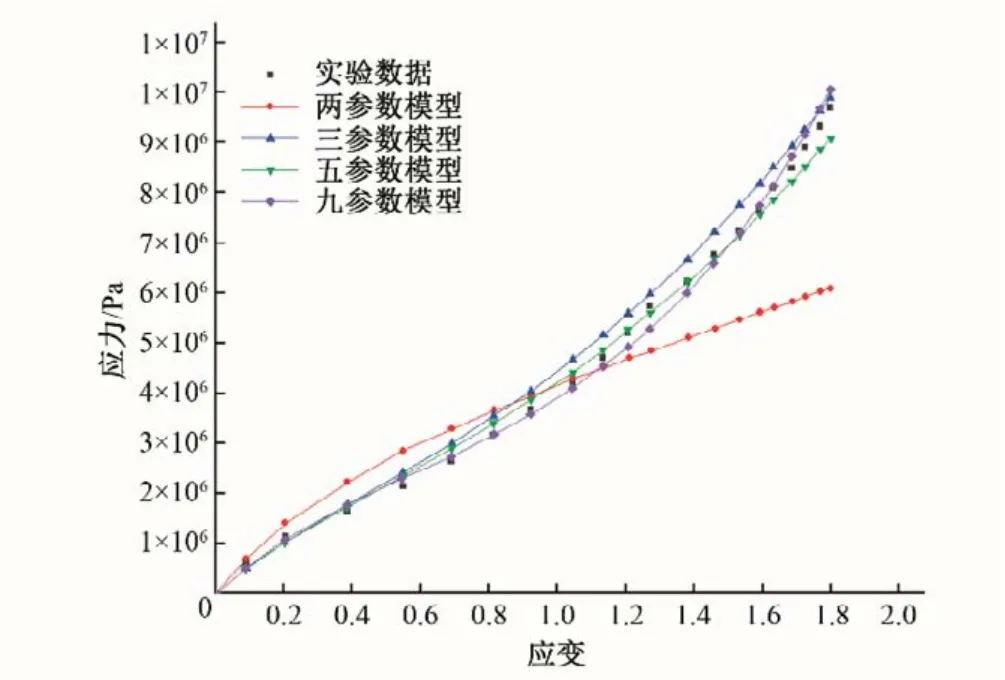
图4 纯剪切试验拟合曲线Fig.4 Pure shear experimental curve fitting

3.2 不同参数M-R模型在工程实例中的比较

由各参数M-R模型拟合曲线的对比可知，参数越多的模型对材料应力应变特性的描述就越精确。但是随着参数的增加，仿真所需的计算量及计算时间也随之增加，为了在提高计算精度和加快计算速率之间取得最优方案，本文以伸缩式水封的预压缩为例，采用各参数M-R 模型分别进行仿真，对比仿真结果从而选取最优方案。

水封材料超弹性参数如表1所示。工程中真实的摩擦系数还需根据材料摩擦试验确定，但本文为探究水封特征参数随库压、止水面板与压板间初始间隙等因素变化的规律，根据《水电工程闸门止水装置设计规范》［18］以橡胶对钢湿摩擦系数0.5 为例进行相关参数分析。选取初始间隙25 mm，背压2 MPa 的工况进行仿真，仿真结果如表2、图5所示。

不同参数M-R模型仿真所得水封接触状态大致相同（如图5），特征参数具体数值有所不同（如表2）。就接触应力而言，二、三、五参数模型仿真结果同九参数模型仿真结果分别相差8.4%、1.1%以及1.7%；就接触长度而言，二、三、五参数模型仿真结果同九参数模型仿真结果分别相差18.4%、0.14%、0.12%。由此可知，三参数、五参数模型的仿真结果同九参数模型的仿真结果相近，二参数模型的仿真结果同九参数模型的仿真结果相差较大。在保证仿真精度的前提下，为提高仿真计算速率及收敛稳定性，建议采用三参数M-R模型进行伸缩式水封的有限元仿真。

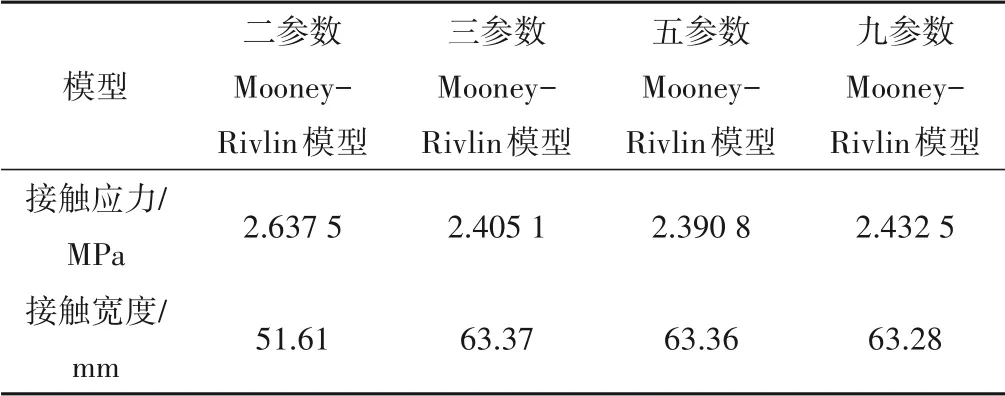
表2 不同模型计算结果Tab.2 Calculation results of different models

图5 九参数模型计算接触应力云图Fig.5 Contact stress nephogram was calculated by M-R model with nine parameters

为验证三参数M-R模型在伸缩式水封仿真中的准确性，使用该模型对水封自由外伸试验进行仿真［19］。仿真结果与试验数据对比表明：使用该模型仿真的结果与试验结果相近（最大误差为7.6%）且变化规律相同（如图6）。该结果验证了三参数M-R 模型用于伸缩式水封仿真中的准确性，因此，本文采用三参数M-R模型进行水封的有限元分析。

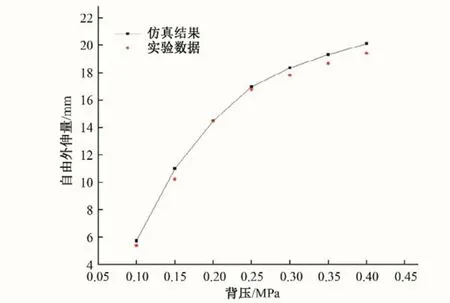
图6 仿真结果与试验数据Fig.6 Simulation results and experimental data

4 仿真结果分析

为探究水封特征参数随所受背压、库压以及止水面板与压板之间初始间隙等因素变化的规律，对不同工况下的水封进行仿真并对仿真结果进行分析。

4.1 背压对自由外伸量的影响

为了确定止水面板同压板之间的初始间隙，首先对水封自由外伸进行仿真，仿真结果如图7所示。由仿真结果可知，水封自由外伸量随背压的增加而增加且增加速率不断减小。背压在0.5 MPa 以下时，水封以结构自身的变形为主，背压达到0.5 MPa 左右时，水封结构自身变形达到极限，此后水封的变形以材料的拉伸为主。因此，自由外伸量在背压0.5 MPa 以下时随背压快速增加，在背压达到0.5 MPa 左右时，增加速率显著降低。此后，由于随着应变增大水封同压板表面之间摩擦的加剧以及过大应变下材料本身的硬化，在背压增大的同时，自由外伸量的增加速率也在逐渐放缓。

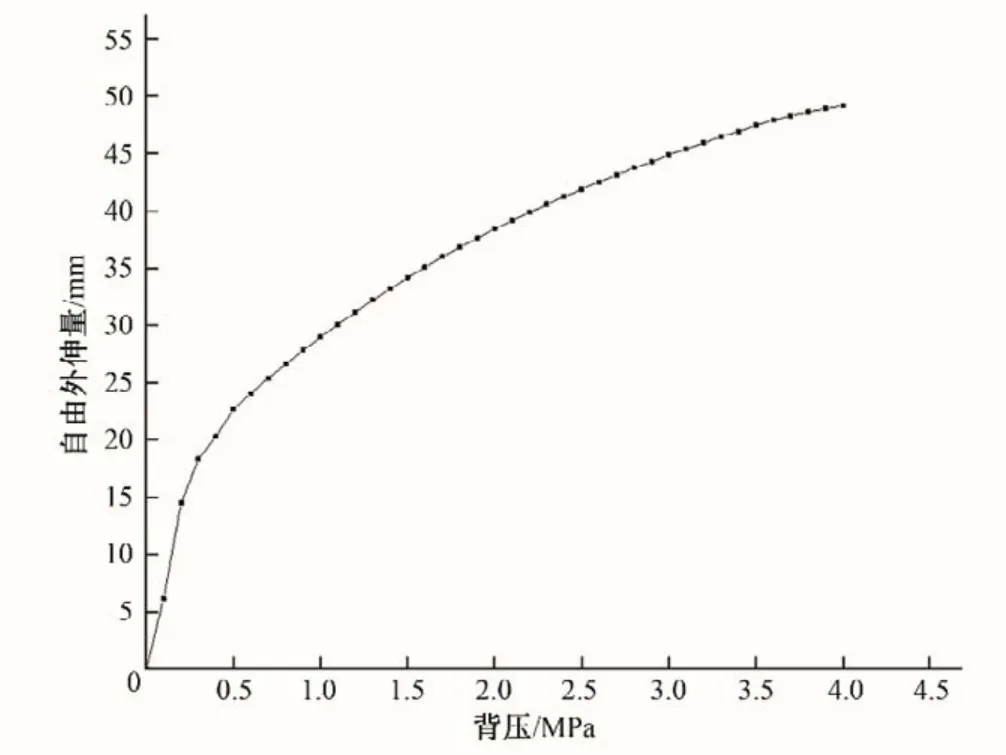
图7 不同背压下封头自由外伸量变化曲线Fig.7 Change curve of free stretch of head under different back pressure

4.2 预压缩接触应力受背压及初始间隙影响

预压缩阶段接触应力主要受止水面板与压板上表面间初始间隙以及水封所受背压的影响，为探究预压缩接触应力随初始间隙以及背压变化的情况，对不同初始间隙、背压下的水封进行仿真。得到了不同背压、初始间隙下封头的最大接触应力（如图8）、不同初始间隙下接触应力的分布情况（如图9）以及不同背压下接触应力的分布情况（如图10）。

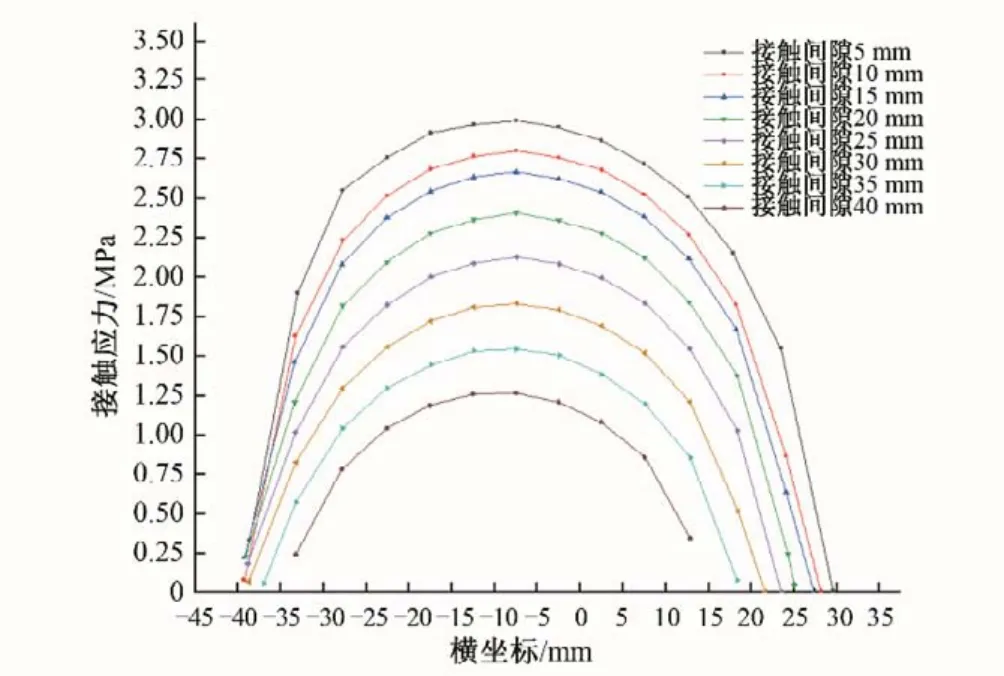
图9 不同初始间隙下接触应力分布情况Fig.9 Contact stress distribution under different initial clearances

如图8所示，接触应力随初始间隙增大而减小，随背压增大而增大。具体的，在背压不变时，接触应力随初始间隙的降低而增加，且在不同初始间隙范围内的增加速率不同。在初始间隙40～20 mm 阶段，接触应力与初始间隙呈近似的线性关系；在初始间隙20～10 mm 阶段，接触应力的增加放缓；在初始间隙10～5 mm 阶段，接触应力的增加速率提升。这主要是由于在不同初始间隙下水封的变形特点及水封两侧同压板间接触情况不同所导致的。此外，在较小背压下水封两侧同压板间接触情况受预压量影响较大，因此这一趋势在较小背压下体现的尤为明显。在初始间隙不变的情况下，接触应力随背压增大而增大，且二者呈近似的线性关系（图10 中横坐标相同的各数据点间纵向距离大致相同）。

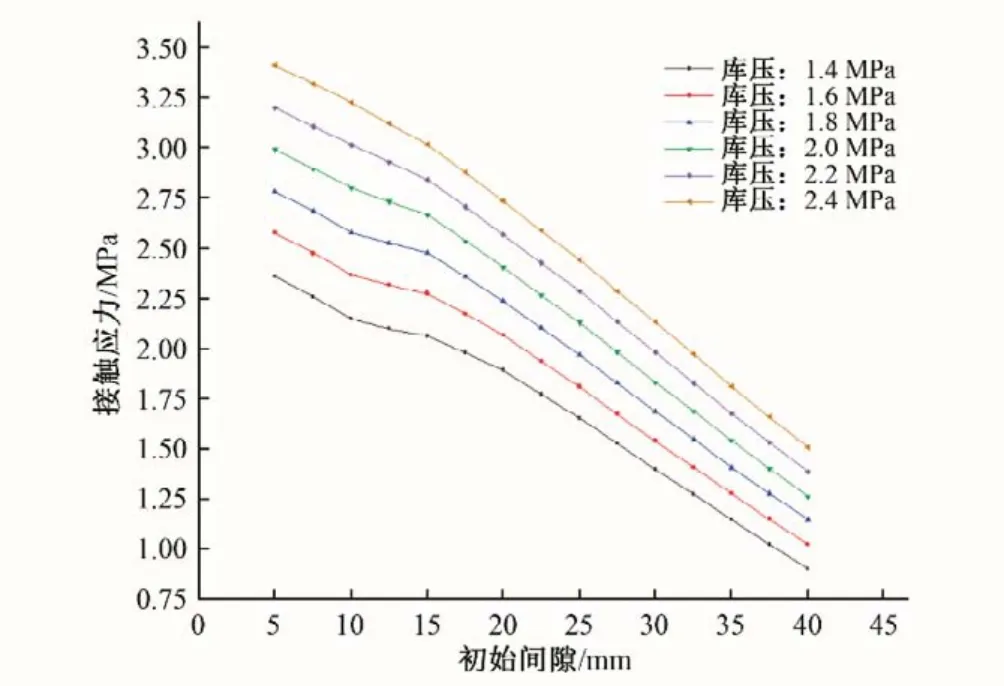
图8 不同背压及初始间隙下的接触应力Fig.8 Contact stress under different back pressure and initial clearance

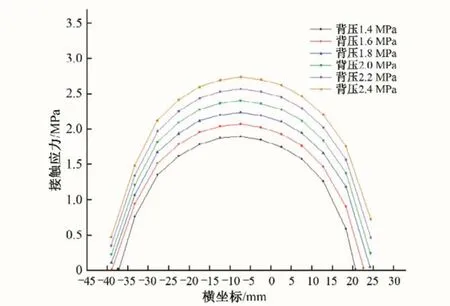
图10 不同背压下接触应力分布情况Fig.10 Contact stress distribution under different back pressures

如图9、10所示，水封接触宽度随初始间隙增大而减小，随背压增大而增大，接触应力分布情况及最大应力位置基本保持不变。

4.3 施加库压后接触应力的变化

伸缩式水封按背压来源可以分为不同种类，其中自封闭伸缩式水封的背压是通过引入库压实现的，因此，该类水封的背压同库压大小一致。由预压缩仿真结果可知：自封闭伸缩式水封在初始间隙大于25 mm 的情况下，水封预压量不足导致接触应力小于库压，不能够有效止水；在初始间隙小于10 mm 的情况下，水封预压量过大导致水封整体变形严重，影响水封工作寿命。综上所述，为保证自封闭伸缩式水封在有效止水的同时能够工作较长时间，止水面板同压板之间的初始间隙应控制在10～25 mm的范围之内。

水封止水过程中还受到库压的作用，因此水封在工作中的受力情况同预压缩阶段并不相同。为探究施加库压后水封同止水面板接触及水封形变情况的变化，本文选取自封闭伸缩式水封能够有效止水范围（库压1.4～2.4 MPa，初始间隙10～25 mm）的水封施加相应的库压并进行仿真分析。得到施加库压前后水封的接触应力变化情况（如表3）及水封受库压后的接触及变形情况（如图11）。

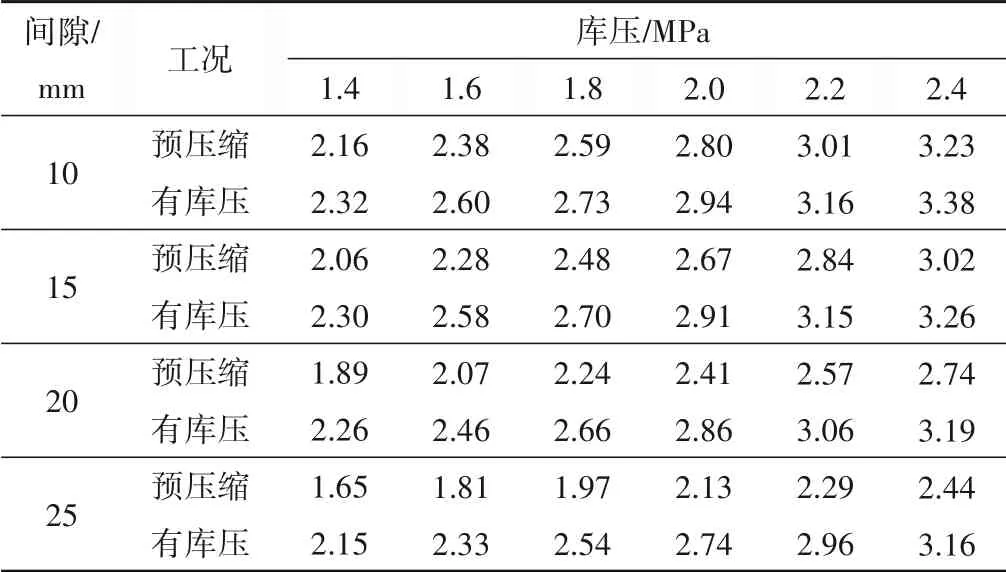
表3 施加库压前后接触应力大小Tab.3 Size of contact stress before and after applying reservoir pressure

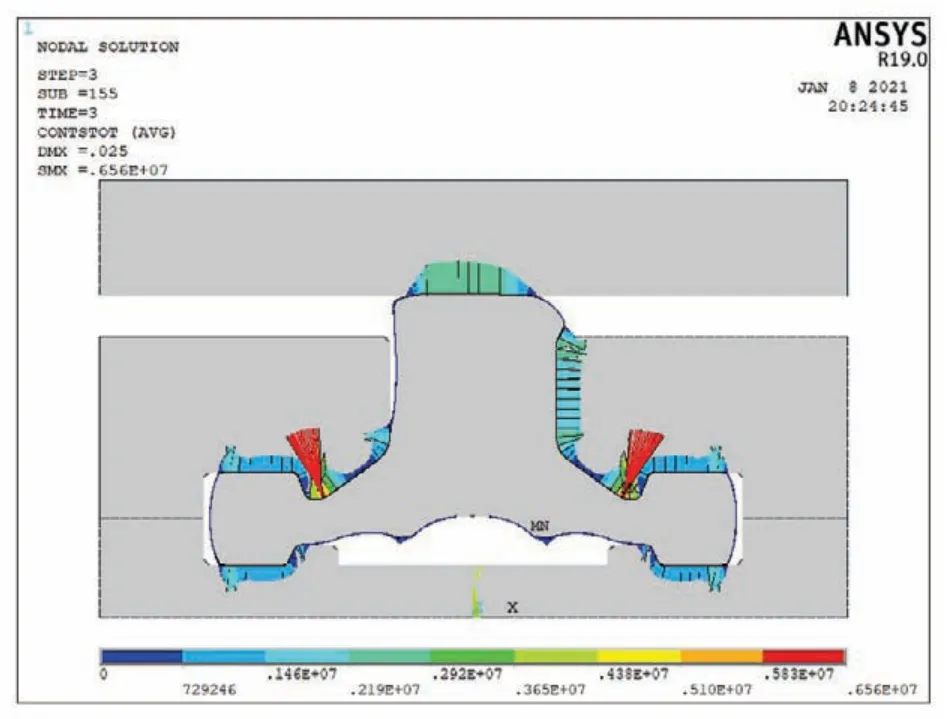
图11 20 mm初始间隙2.0 MPa库压下水封接触应力云图Fig.11 Contact stress nephogram of water seal under reservoir pressure with initial clearance of 20 mm and 2.0 MPa

由表3可知，相较于预压缩阶段，施加库压后水封的接触应力明显增大。这主要是由于水封封头形状不对称且库压施加在封头较高一侧，封头在库压及止水面板的共同作用下受挤压所导致的（如图11）。因此，封头不对称的自封闭伸缩式水封，在预压缩可靠的情况下施加库压，不仅不会因为库压导致止水失效反而会因为库压导致的水封变形使得水封接触应力增大，止水可靠。

4.4 外偏移量受库压及初始间隙的影响

对水封施加库压，除了使接触应力发生变化，还会加剧封头的偏移。为探究水封外偏移量受库压及初始间隙的影响，将施加库压后水封封头的外偏移量提取出来，结果如图12所示。

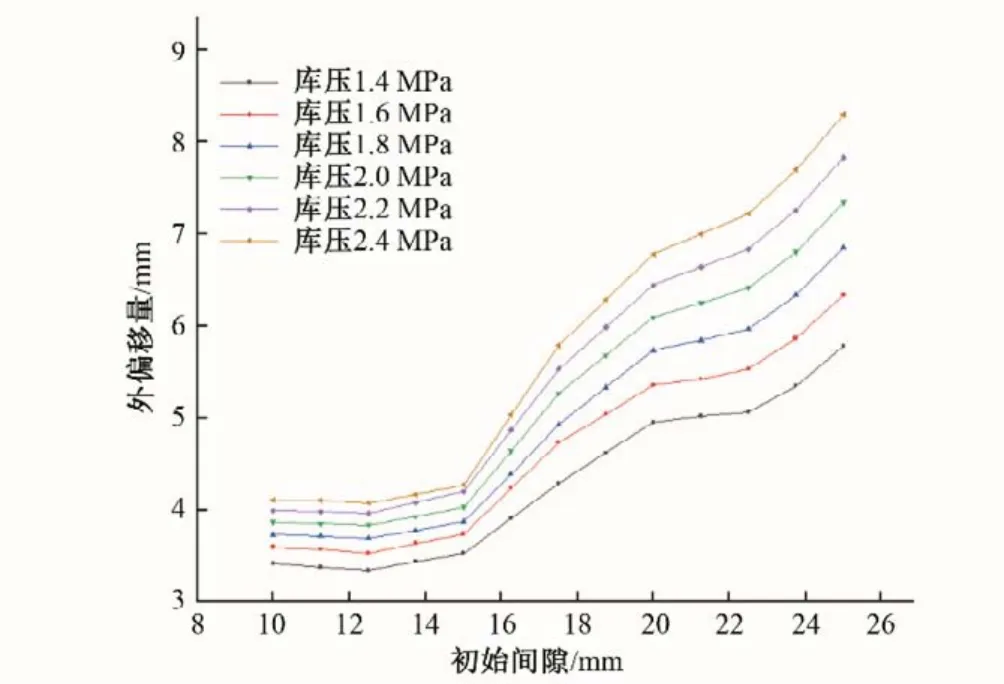
图12 不同库压及初始间隙下的外偏移量Fig.12 External offset at different reservoir pressures and initial clearances

由结果可知，在初始间隙相同时，水封外偏移量随库压的增加而增加。在库压相同时，水封外偏移量随初始间隙的变化在不同阶段有不同的特点。在初始间隙10～15 mm 阶段，水封外偏移量很小且随初始间隙变化不大。这主要是由于在初始间隙很小时，库压的作用范围很小且封头大部分部位被右侧压板阻挡。在初始间隙15～22.5 mm阶段，水封外偏移量随初始间隙增加而增加，且增加速率随着初始间隙的增大而减小。这主要是由于水封材料随着应变增大产生硬化以及止水装置结构限制所导致的。在初始间隙大于22.5 mm 阶段，外偏移量随初始间隙增加的速率显著提升。这主要是由于在初始间隙较大时库压作用范围较大以及止水面板对封头摩擦阻碍作用的下降所导致的。