微分经验模态分解和能量矩阵相结合的水电机组故障信号预处理方法研究

吴俊健，舒锦宏，徐灵江，吕延春，段文华，潘天航

（1.国网浙江省电力有限公司紧水滩水力发电厂，浙江丽水320000；2.国网浙江电力调度控制中心，杭州310007；3.南京南瑞继保电气有限公司，南京211102）

0 引言

水电机组状态监测和故障诊断的关键是对采集信号的处理，通过信号处理手段，提取有效的故障特征来定位故障点，能够提高检修效率和预防故障发生［1］。目前应用比较广泛的信号处理方法有短时傅里叶变换［2］、小波变换［3-5］、希尔伯特黄变换［6，7］和独立分量分析［8-10］等。经验模态分解（Empirical Mode Decomposition，EMD）依据数据自身的时间尺度特征对信号进行分解得到本征模态函数（Intrinsic Mode Function，IMF），各IMF 分量包含了不同时间尺度的局部特征信号［11］。EMD 的约束条件为局部极大值包络和局部极小值包络的平均为零，信号的波形局部对称。水电机组振动故障信号通常具有间歇性、且包含噪声，因此使用EMD分解求取局部的极值时候容易出现偏差，使得同一个IMF 中会包含不同的频率分量，这就是模态混叠现象。模态混叠现象使得各个IMF 不能准确表现原始信号的频率特性，这影响使用EMD进行水电机组振动信号处理的准确性［12］。

为解决上述模态混叠的问题，研究学者通常使用改进的EMD 算法。李辉等使用EEMD 方法对水轮机振动信号进行分解，能够削减模态混叠效应更准确的进行奇异谱分解［13］；何葵东等使用EEMD 多尺度熵方法筛选有效的本征模态分量，能够减少模态混叠干扰对水电机组振动信号特征提取的影响［14］；徐艳春等采用EMD 自相关阈值的方法对水电机组振动信号进行去噪，能很好减少模态混叠干扰［15］等。以上做法均是综合利用多种信号处理手段对信号进行分析，并未涉及到信号本身高阶微分特性。对微分信号进行经验模态分解能有效抑制信号混叠失真的情况，并且其特征频率的筛选效果要优于传统的经验模态分解方法［16］。因此，本文提出了一种微分经验模态分解和能量矩阵相结合水电机组故障信号预处理方法。首先利用多重微分增强高频分量，再对各阶微分信号进行EMD 分解，使用分解得到的IMF 分量构造原始信号的微分信号的能量矩阵，由此来对机组的有效信号进行筛选。本文使用该方法对国内某电站水导轴承和下导轴进行处理，能够精准分辨出有效的能量特征信号，使用支持向量机对结果进行验证，微分经验模态分解后的识别精度大大提高。

1 算法分解

1.1 经验模态分解算法

NordneE.Huang 等人提出了本征模函数（Intrinsic Mode Function，简称IMF）的分解算法。EMD 分解原始信号获取IMFs的过程被称作“筛选”过程，整个筛选过程如下：

（1）首先计算出目标信号x(t)全部局部极值点，采用三次样条插值法对局部极大值和局部极小值序列进行插值运算，得到x(t)的上包络线u1(t)和下包络线l1(t)。

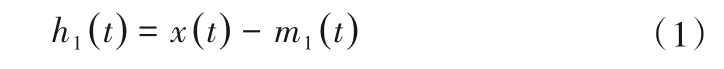
（3）根据IMF 条件判断是否需要继续进行“筛选”，筛选的过程就是以该中间信号为新的输入信号继续重复1～2 的步骤。筛选过程通常在残数只包含不超过两个极值时停止。

（4）由于第一次分解后的余量信号r1(t)中依然会含有不同时频尺度的分量，因此，将前一次的分解余量r1(t)作为目标信号，重复上述步骤继续对信号进行分解，获得余量信号的IMF分量：

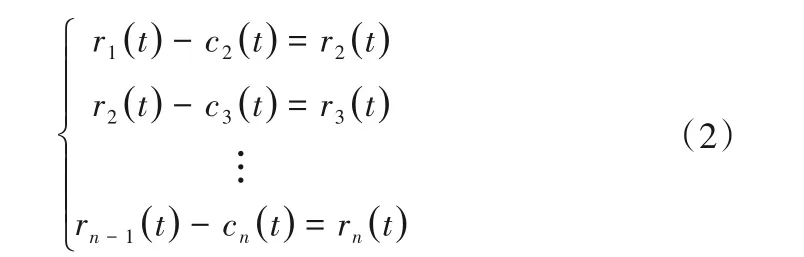
判断余量信号rn(t)为一个单调函数或者值足够小时，可以忽略最后一阶余量信号，分解结束，原始信号x(t)分解最终得到IMFs集合：

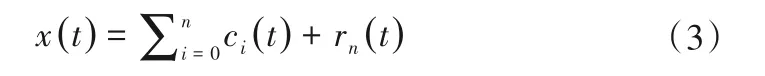
1.2 微分经验模态分解

为了改善模态混叠现象，可以将恢复高频分量极值点作为切入点。微分运算具有不改变原有信号的频率组成和能够根据各分量频率线性增加其幅值的特性。因此首先通过微分运算增加高频分量幅值，再进行EMD 分解，这样更有利于实现极值点的恢复。微分经验模态分解过程如下：

（1）推求出原始信号的各阶微分信号，与原始信号一起形成目标信号集XT：

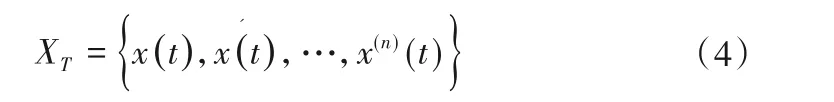
（2）对集合XT中的各信号分别进行EMD 分解，将各阶信号及其分解的本征模函数组合起来构成本征模函数矩阵MIMF：

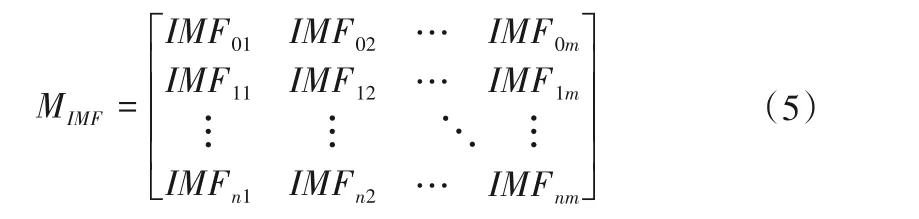
矩阵中：第一行IMF01-IMF0m为原始信号的本征模函数集，第二行至第n+1 行则分别对应于一阶到n阶微分信号的本征模函数集。各阶微分信号的分解所得的本征模函数的个数一般不同，因此在构建矩阵时选择各阶分解IMF 信号最多的个数m作为矩阵的长，其余分解IMF 个数不足m个的，在矩阵中补0。

1.3 构造能量矩阵

（1）分别由式（6）计算出各个IMF 分量的能量Ei由式（7）计算出各IMF能量所占总能量比例：

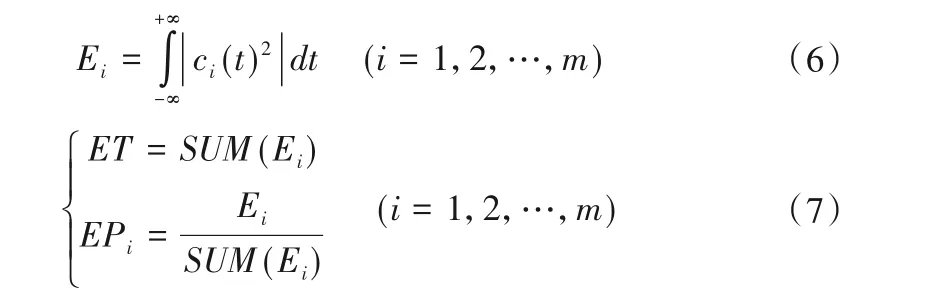
（2）最终将ET和EPi联合起来构成能量分布特征向量FV=[ET，EP1，…，EPm]，分别从宏观和微观两个方面描述信号的能量特征。

2 仿真算法

2.1 模态混叠效应

构建式（8）仿真信号，以sin(2πt)为基频分量线性构造x1(t)和x2(t)，其中x2(t)多了叠加一个2倍频分量。

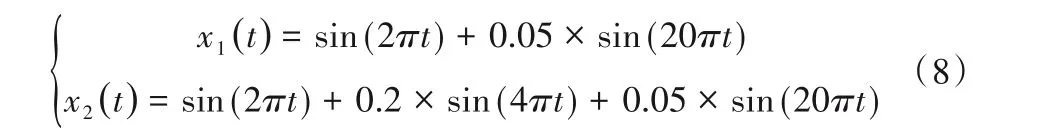
分别对x1(t)和x2(t)进行EMD 分解，得到其本征模函数集分别如图1（a）和图1（b）所示，计算其能量分布特征向量如表1所示。

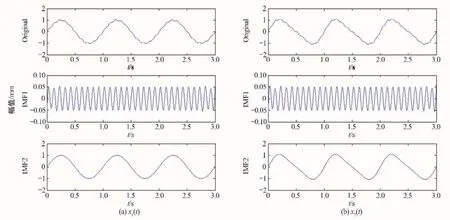
图1 EMD分解结果x1（t）和x2（t）Fig.1 EMD decomposition results x1（t）and x2（t）

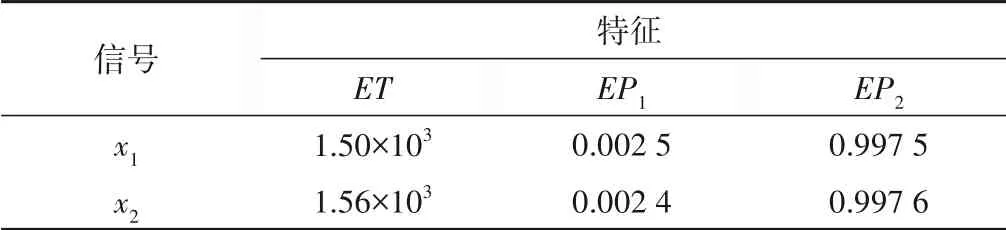
表1 EMD分解能量分布特征Tab.1 EMD decomposition energy distribution characteristics

分析图1可以发现：x1(t)经过EMD 分解后明显得到基频分量和10 倍频分量，而x2(t)经过EMD 分解后并没有将基频分量和叠加的2 倍频分量分离开来。观察表1 的能量特征，x1(t)和x2(t)也十分接近，不能识别出两个信号的不同。这使得两个不同信号x1(t)和x2(t)经过EMD 所得的本征模函数集却比较接近，由此而得出的信号特征也将难于进行有效区分。这就是模态混叠效应。

2.2 消除模态混叠效应

使用本文介绍的微分经验模态分解对上述仿真信号进行分析，得到x1(t)和x2(t)的本征模函数集，结果如图2（a）和图2（b）所示。计算其能量分布特征向量如表2所示。

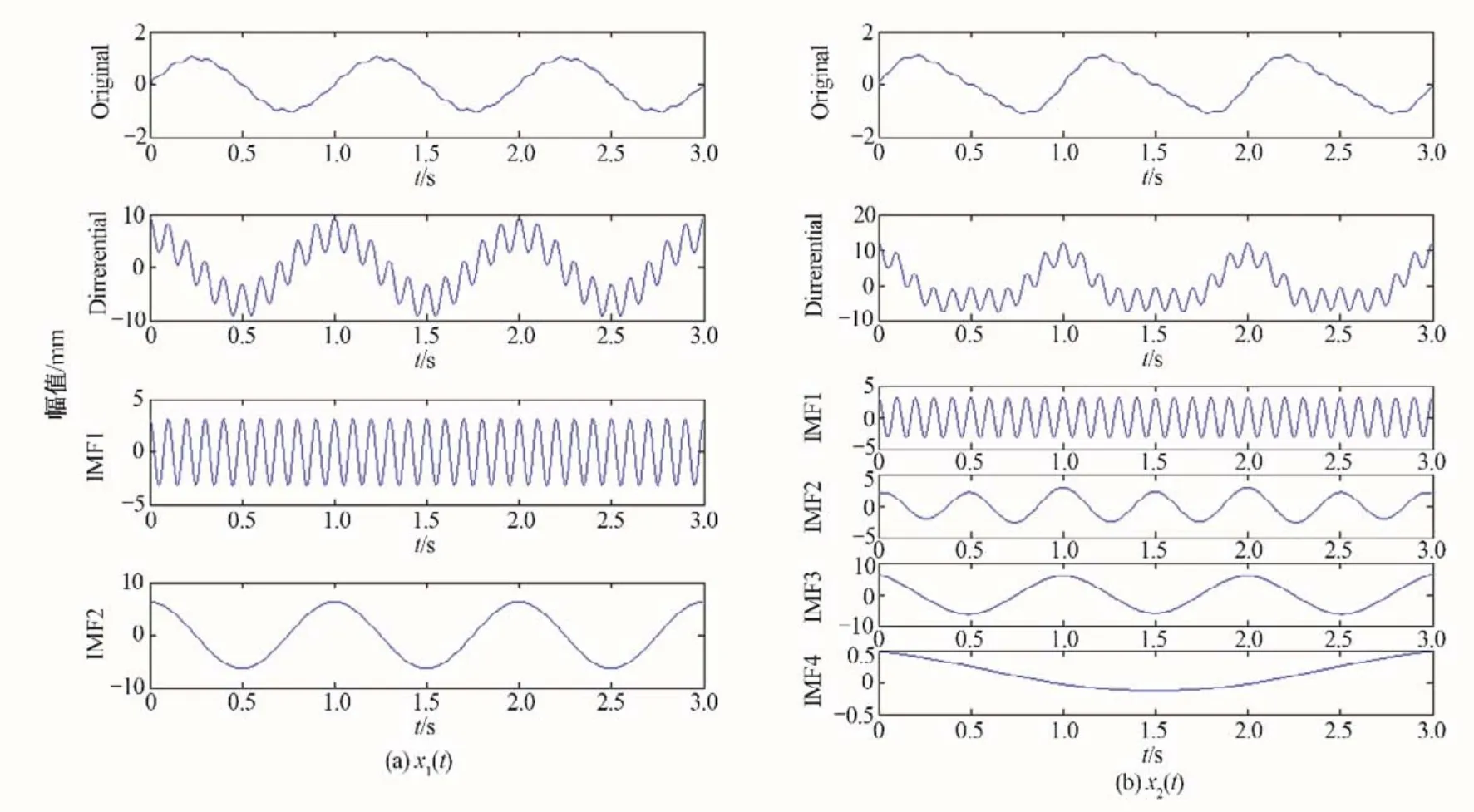
图2 微分EMD分解结果x1（t）和x2（t）Fig.2 Differential EMD decomposition results x1（t）and x2（t）

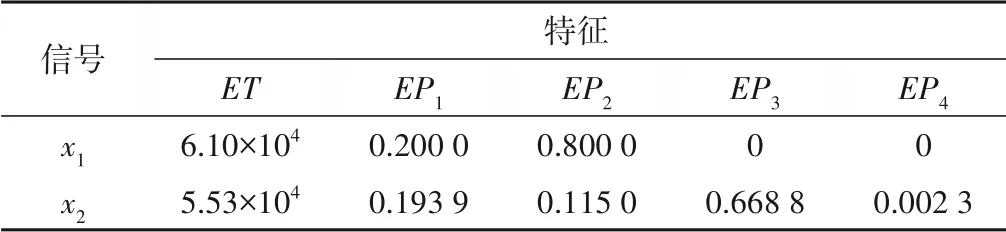
表2 通过微分EMD分解能量分布特征Tab.2 Decompose energy distribution characteristics by differential EMD

分析图2 可以发现：x1(t)经过微分后的本征模函数波形包含了基频和10倍频的特征信号，x2(t)经过微分后的本征模函数波形分离出了基频、10 倍频的特征以及和基频混叠的2 倍频分量。由表2 查看能量特征表也能发现x1(t)和x2(t)有明显的区别。通过以上对比分析可以证明微分经验模态分解构造能量矩阵的方法可以有效改善EMD模态混叠效应。

3 水电机组实测信号分析

国内某水电站基本参数如下：设计水头126.65 m，最高水头143 m，额定水头111 m，最小水头83 m，水轮机转轮型号为HL211-LJ-577.5，额定转速136.4 r/min。2 号机组运行过程中出现异常振动现象，从监控历史数据库中取得水导轴承x、y向摆度信号和下导轴承x、y向摆度信号。相同工况条件下，取出40个数据样本，其中选择25个作为训练数据集，剩余15个作为测试数据集。分别对四组原始信号、一阶微分信号、二阶微分信号做EMD分解，分解结果分别如图3、4和图5所示［其中分图（a）、（b）、（c）、（d）分别代表水导x向、水导y向、下导x向、下导y向］，并计算其能量分布特征矩阵如表3所示。

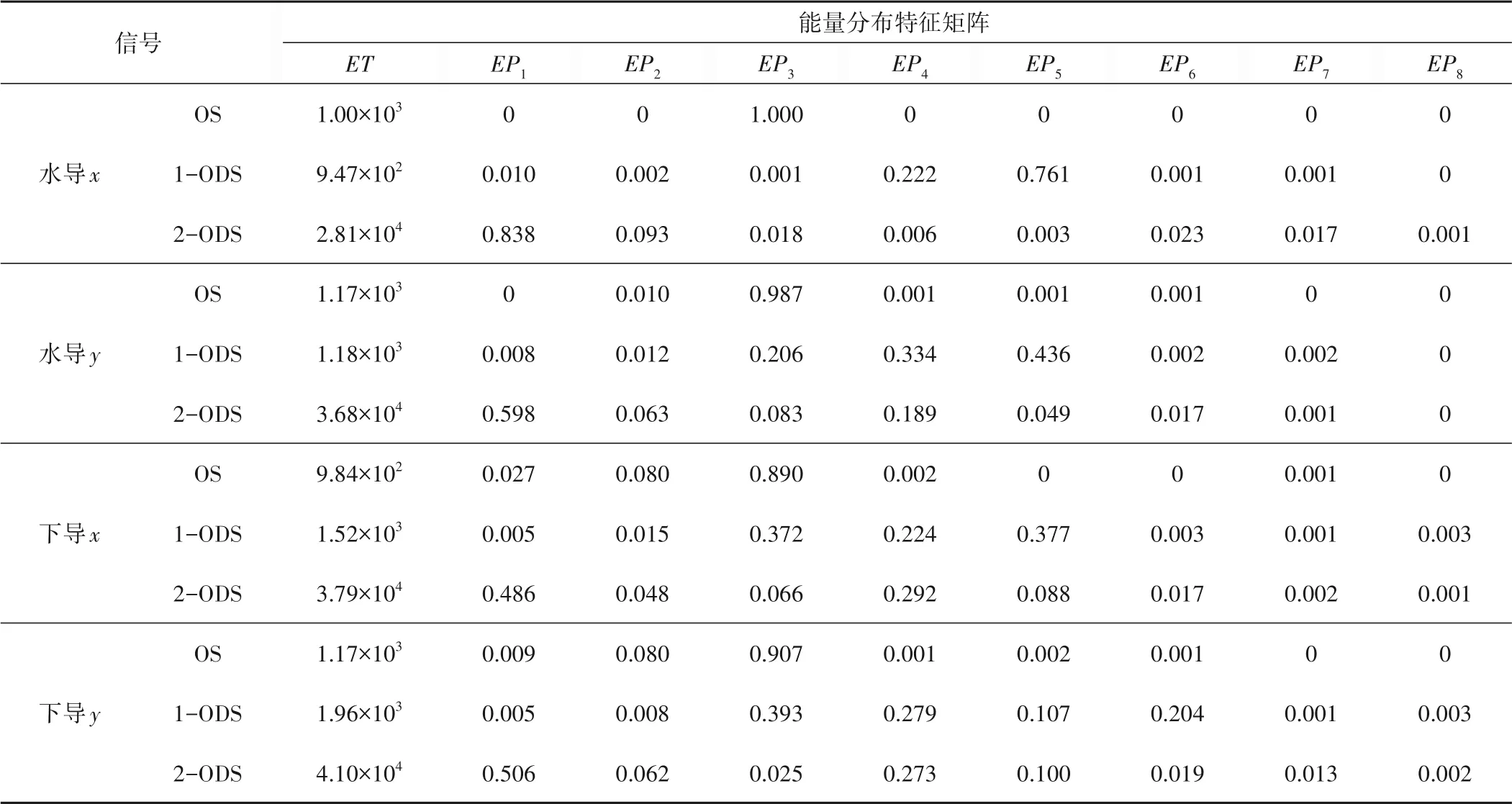
表3 四类信号能量分布特征矩阵Tab.3 Four types of signal energy distribution eigenmatrix

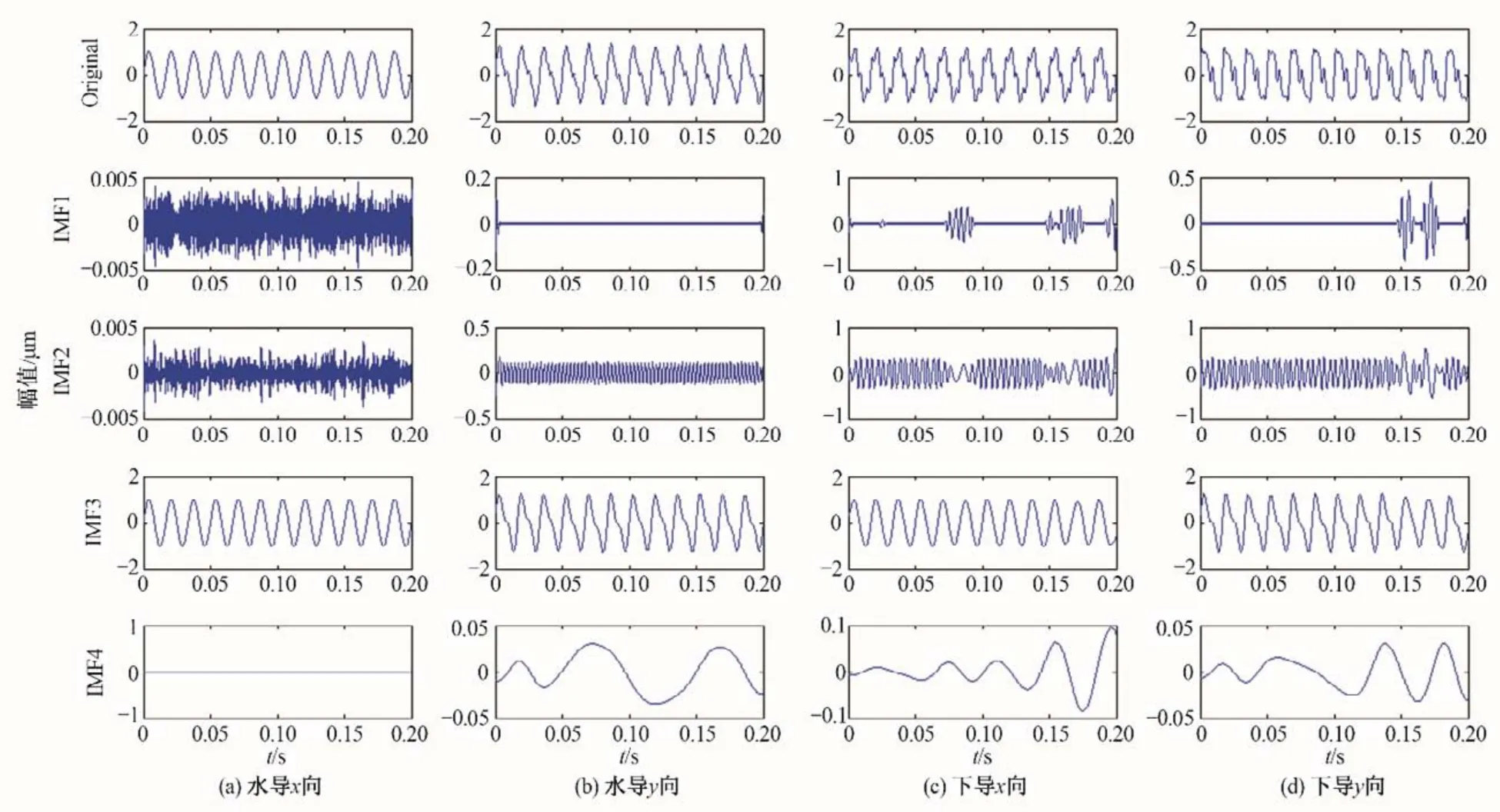
图3 原始信号（Original signal，OS）的EMD结果Fig.3 EMD results of Original signal（OS）

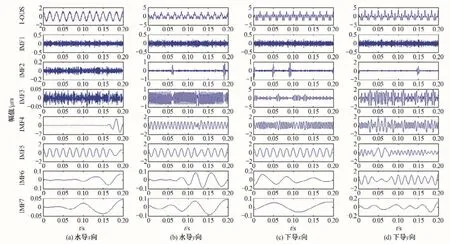
图4 一阶微分信号（1-order differential signal，1-ODS）的EMD结果Fig.4 EMD results of 1-Order Differential Signal（1-ODS）

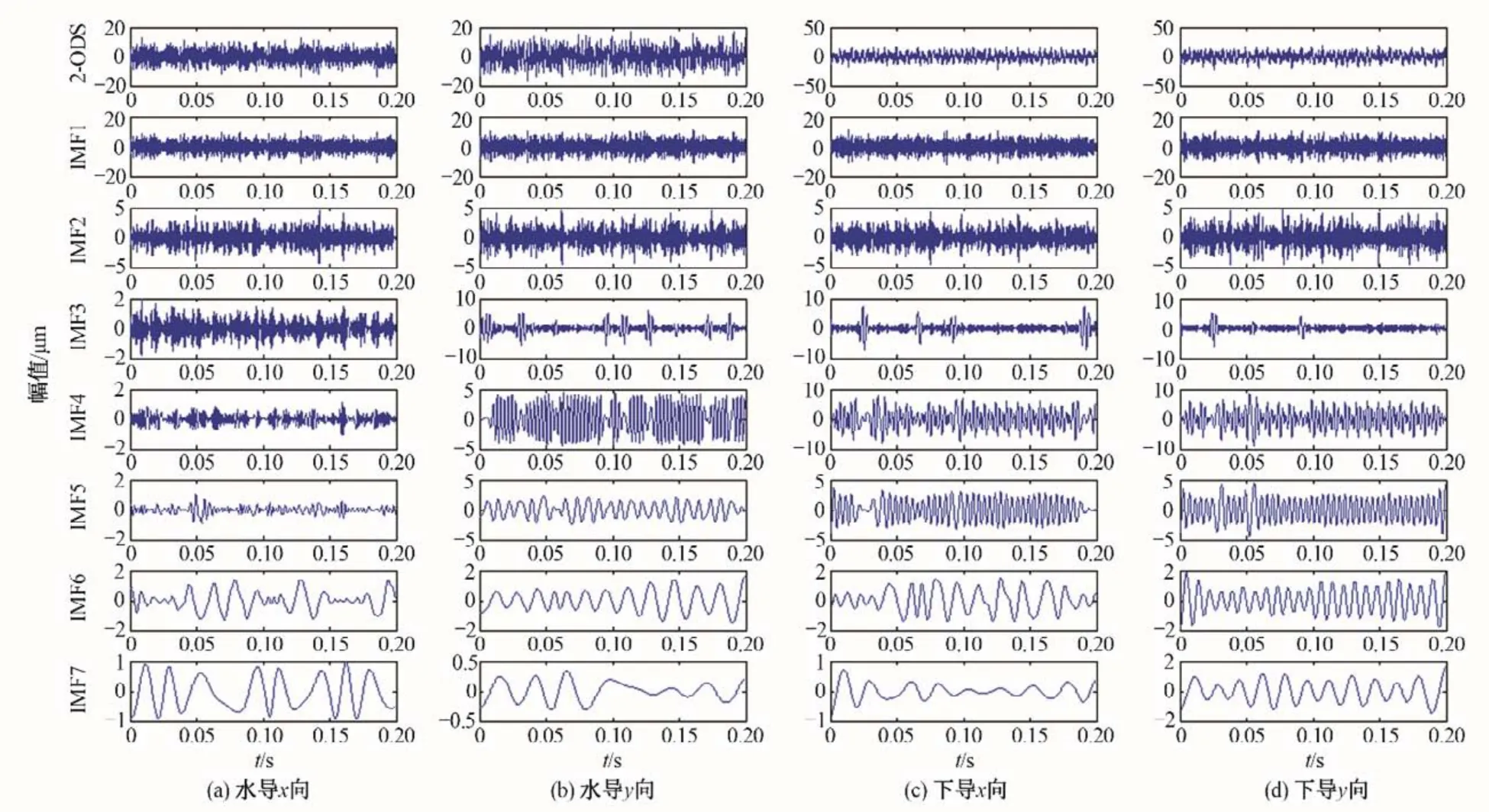
图5 二阶微分信号（2-order differential signal，2-ODS）的EMD结果Fig.5 EMD results of 2-order differential signal（2-ODS）

引入支持向量机（Support vector machine，SVM）对上面构造的4 组信号进行分类实验，对比验证微分经验模态分解和能量特征矩阵相结合方法的有效性。通过SVM 四类信号的25 组训练集进行学习，完善自身模型参数，之后通过识别的模型对四类测试样本进行对比测试，测试结果如表4所示。查看每组信号的常规EMD识别精度、1阶EMD识别精度和2阶EMD识别精度发现支持向量机的识别精度随着微分阶数提高明显提高，2阶微分信号的EMD 识别精度基本达到100%。计算4 组测试信号测试样本原始信号、1 阶信号、2 阶信号识别精度的平均值分别为65.3%、94.2%和98%。上述测试证明微分经验模态分解方法能够有效解决传统EMD分解出现模态混叠的问题，通过微分经验模态分解信号构建能量矩阵能够有效表征信号的组成特性，该方法作为水电机组振动信号的预处理手段有良好的效果。

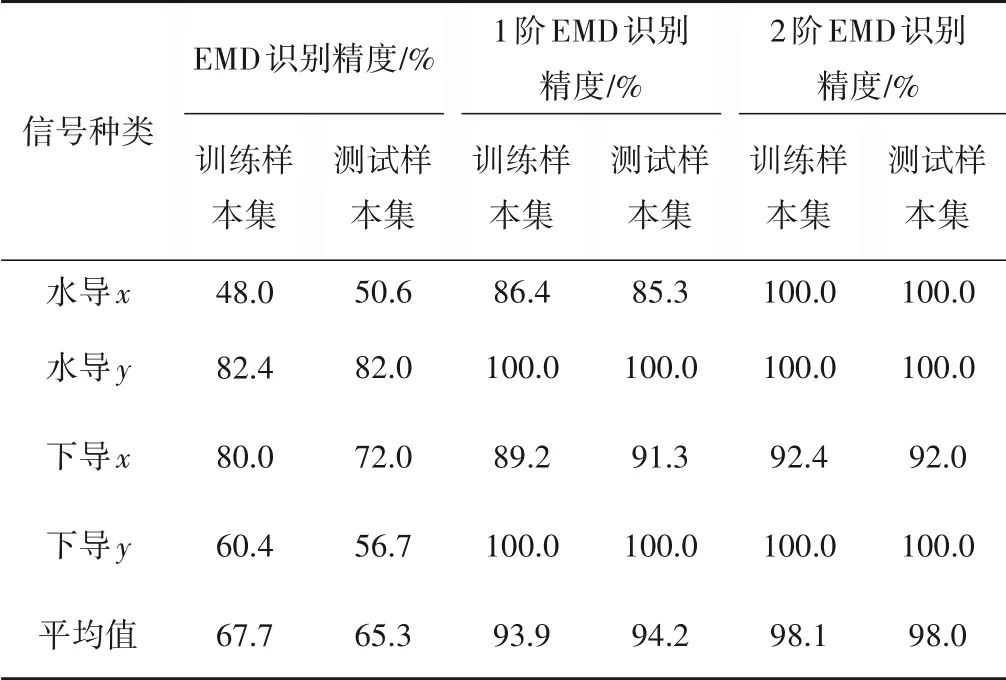
表4 仿真信号识别结果Tab.4 Simulation signal identification results

4 结论

本文为解决使用EMD 分析水电机组振动信号过程中存在的模态混叠问题，使用微分经验模态分解方法对可能被“淹没”于原始信号中的高频极值点进行恢复，增加EMD 分解的准确性。随后构造出信号的能量分布特征矩阵，通过数据仿真证明该方法能有效规避模态混叠效应。使用支持向量机对复杂实测信号进行对比验证，发现2 阶EMD 的识别精度大大提高，证明微分经验模态分解在解决模态混淆方面的有效性。该方法对于处理复杂的水电机组振动信号有实际意义，可作为有效的信号预处理手段，筛选出能量特征明显的数据进行故障分析。□