基于B2B-MMC的柔性互联变电站优化调度方法
2022-04-12班国邦张腊华袁旭峰马晓红欧阳泽宇
班国邦,张腊华,袁旭峰,马晓红,欧阳泽宇,刘 丽
(1.贵州电网有限公司电力科学研究院,贵州贵阳 550002;2.南方电网公司防冰减灾重点实验室,贵州贵阳 550002;3.贵州大学电气工程学院,贵州贵阳 550025;4.贵州电网有限公司毕节供电局,贵州毕节 551700)
0 引言
近年来,随着功率半导体的飞速发展,进一步推进柔性互联技术成为智能电网的重要研究方向之一[1-4]。由于传统配电网依赖“硬”开关的控制方式无法满足灵活、主动调控潮流的需求,为此引入智能软开关(Soft Open Point,SOP)以适应智能电网的建设需求。背靠背模块化多电平换流器(Back to Back Modular Multilevel Converter,B2B-MMC)具备灵活潮流调控能力,能实现实时、快速、平滑的功率控制,保障区域间的潮流互济,极大提升配电网可靠性和灵活性[5-9]。2018 年由国家电网有限公司设计的世界首个柔性变电站投入运行,将新型电力电子技术与变电站技术相结合,实现新能源与多元化负荷的柔性接入,提升了电网的经济、安全、高效运行水平[10-11]。
目前柔性变电站在配电网系统控制和优化调度方面已有一定研究成果,为配电网的整体优化运行奠定了基础[12-13]。文献[14]通过分析张北10 kV柔性变电站在有源配电网中节能降损等功能,进一步说明了柔性变电站在配电网中的实际效益。文献[15]提出一种以电力电子变压器(Power Electronic Transformer,PET)为载体的柔性变电站结构,同时实现交、直流电压之间的相互转换和电气隔离,通过局部控制实现网侧与负荷之间的潮流控制,所设计的控制策略可保证柔性变电站稳定运行。文献[16]以含柔性变电站的交直流配电网为研究对象,提出一种基于目标级联法的分布式优化调度方法,柔性变电站同时兼顾中压交流、中压直流、低压直流系统,可实现“源-网-荷”之间的协调互动与交直流系统的经济运行。
SOP 作为柔性接入配电网的可控媒介,在配电网运行控制和优化调度中均是升级改造的重点。在配电网运行控制方面:文献[17]提出一种直接式SOP结构,采用AC-AC 级联模块灵活控制互联馈线环网潮流,在恢复供电方面优势显著。文献[18]提出一种基于双钳位子模块的多端SOP 拓扑结构,其优点在于控制策略和运行模式灵活多样,能够有效提升线路之间的联络关系,提高配网转供能力及可靠性。在配电网优化调度方面:文献[19]将SOP 应用于有源配电网中,采用改进型遗传粒子群混合优化算法对所提模型进行双层优化,以解决配电网中大规模多变量非线性优化问题。文献[20]提出一种基于SOP接入配电网的拓扑结构,建立含SOP 支路的配电网动态优化调度模型,提高了设备调节的主动灵活性。
综上所述,现阶段的研究将B2B-MMC 与变电站相融合以促使系统空间上的潮流分布适应负荷多元化需求[21],研究基于B2B-MMC 的柔性互联变电站运行优化技术具有较好的实用价值和现实意义。为此,本文提出一种基于B2B-MMC 的柔互联变电站优化调度方法,通过柔性互联变电站间的优化协同控制降低了系统网络损耗,实现配电系统潮流的主动调控。
1 柔性互联变电站系统架构及运行控制策略
1.1 系统架构
B2B-MMC 以新型电力电子装置为基础,通过控制指令值实时调整换流器功率输出值,从而改变系统潮流分布。本文针对配电网110 kV/10 kV 双主变系统,提出一种采用B2B-MMC 替代传统断路器及分段开关的柔性互联变电站系统架构,如图1 所示。

图1 柔性互联变电站系统架构Fig.1 Architecture of flexible interconnected substation system
图1 中,B2B-MMC 由MMC1 和MMC2 构成,O1和O2分别为MMC1 和MMC2 的容量,P1+jQ1和P2+jQ2分别为10 kV 母线等效负载,j 为虚部,QC 和QF 分别为电网联络开关和断路器。该架构实现了以下4 个方面的功能:
1)母线互联。实现区域间能量互通、无功补偿功能,为母线电压提供相互支持。
2)主变负载均衡。降低设备过载风险,提高供电可靠性。
3)不停电转供。主变故障时实现快速隔离和非故障区的快速恢复,增强系统稳定性。
4)系统潮流优化。柔性互联态可以提升配电网传输容量以及丰富线路传输路径,有利于实现系统潮流最优分布控制。
在含B2B-MMC 的柔性互联变电站投入运行时,QF 和QC 处于断开状态。
1.2 运行控制策略
基于B2B-MMC 的柔性配电系统中,根据不同运行场景将换流站之间的通讯状态分为有通信控制与无通信控制。有通信控制状态下采用主从控制,无通信控制状态下采用电压下垂控制。
1.2.1 主从控制策略
通常状态下B2B-MMC 采用主从控制,其外环控制需固定2 个控制自由度。主换流站的有功类控制采用定直流电压控制,以保证换流站的直流节点电压为设定值;从换流站的有功类控制采用定有功功率控制,以保证换流站注入的有功功率为设定值。
针对多端柔性互联系统,设定系统具有n个直流节点,则系统主从控制策略对应模型为:

式中:ΔP1i为主从控制模式下节点i的失配功率;Prefi为换流器设定初始有功功率;PGi,PDi分别为节点i上发电机发出的有功功率和负荷吸收的有功功率;Udci,Udcj分别为节点i,j的直流电压;Rij为节点i,j之间的线路电阻。
1.2.2 直流电压下垂控制策略
直流电压下垂控制是指多个换流站的有功类控制均为直流电压下垂控制,为保证多个换流站的直流节点电压稳定运行,需根据自身特性曲线中的下垂系数ei来增加注入的有功功率。节点i处运行特性为:
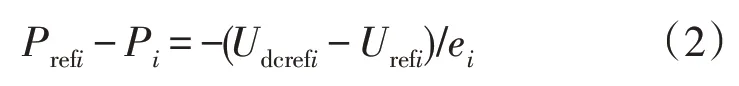
式中:Pi为换流器实际输出有功功率;Udcrefi为直流节点设定的电压值;Urefi为直流节点实际电压值。
针对多端柔性互联系统,设定节点1~w为直流电压下垂控制,节点w+1~k为定有功功率控制,则系统的直流电压下垂控制策略对应模型为:

式中:ΔP2i为直流电压下垂控制模式下节点i的失配功率。
通过对B2B-MMC 换流器控制模式的分析可知:在不同控制方式下其模型结构不同,形成关于状态变量的求解也不一致。主从控制能够实现换流器输出功率的准确控制,该策略简单清晰易于实现,据此本文采用主从控制模式进行求解。
2 含柔性互联变电站的配电网优化调度分析
换流站采用可关断电力电子器件,保证其能够灵活地控制相关交流系统节点的有功和无功变量。在换流器系统中表现为定有功控制、定无功控制,进而可以得到换流器控制策略及等效关系,如表1 所示。

表1 换流器控制策略及等效关系Table 1 Control strategy and equivalent relation of converter
表1 中,P为定有功功率控制,Q为定无功功率控制,Udc为定直流电压控制,Pdc为直流侧有功功率,Ps为交流系统传输到换流器的有功功率,Ploss为换流器损耗功率。对于换流器采用P/Q控制时,交流侧将其等效为PQ节点,直流侧将其等效为P节点;换流器采用Udc/Q控制时,交流侧将其等效为PV节点,直流侧将其等效为V节点;换流器采用电压下垂/Q控制时,交流侧将其等效为PQ节点,直流侧将其等效为电压下垂节点。
2.1 B2B-MMC等效模型及功率特性
柔性互联变电站中B2B-MMC 换流站拓扑等效模型如图2 所示,该模型主要包括交流系统模型、B2B-MMC 模型和直流系统模型。
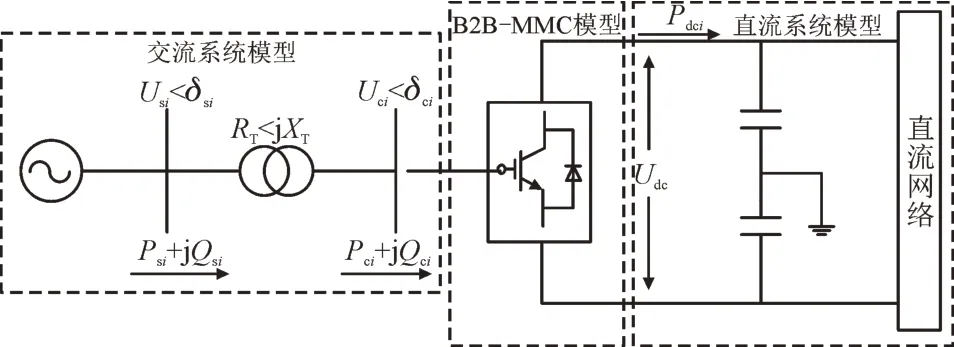
图2 B2B-MMC换流站拓扑等效模型Fig.2 Equivalent model of B2B-MMC converter station topology
图2 中,RT和XT分别为变压器和B2B-MMC损耗等效阻抗,Psi和Qsi分别为母线到换流变压器的有功功率和无功功率,Usi和Uci分别为母线两侧电压幅值,Pci和Qci分别为换流站侧母线的有功功率、无功功率,Udc为换流站侧母线的直流电压,δsi和δci分别为母线两侧电压相角,Pdci为直流侧节点i的有功功率。
根据模块化多电平换流器功率特性,得到交流侧潮流方程、交流测流入换流器的潮流方程。
交流侧潮流方程为:
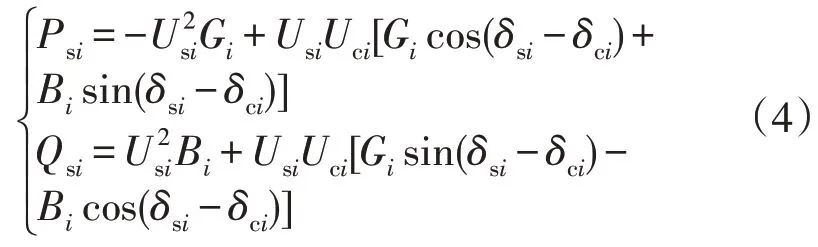
式中:Gi,Bi分别为交流系统线路等效电导和电纳。
交流测流入换流器的潮流方程为:

2.2 MMC功率约束
针对图1 中的MMC1 和MMC2,主从控制模式下换流站功率输出及容量需要满足式(6),即:

式中:PMMC1和PMMC2分别为换流器注入的有功功率;QMMC1和QMMC2分别为换流器注入的无功功率。
2.3 主变压器约束
为防止等效负荷功率加上B2B-MMC 输出功率超出变压器承载能力,其约束条件为:
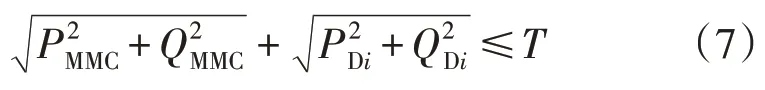
式中:PMMC和QMMC分别为换流器注入的有功、无功功率;PDi和QDi分别为与换流器连接点处的等效有功、无功功率负荷;T为变压器容量。
2.4 目标函数
基于B2B-MMC 的含柔性互联变电站的优化调度作为控制目标与控制手段之间的桥梁,在配电网运行过程中利用遗传算法(Genetic Algorithm,GA)对换流器功率设定值进行赋值,根据改进交替迭代法[22-23]计算出的最优结果可不断修正换流器功率设定值,实现系统网损最小化。本文将目标函数设置为网损最小,其中换流器有功损耗约为注入功率的1%[24-25],则高压电网网络损耗功率为:
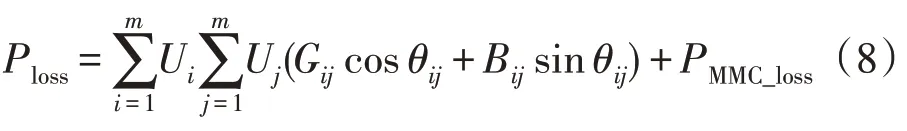
式中:Ploss为高压电网网络损耗功率;Ui和Uj分别为节点i,j的电压幅值;Gij,Bij,θij分别为节点i,j之间的电导、电纳和相角差;m为交流系统节点数;PMMC_loss为换流器损耗值。
考虑配电节点电压裕度约束,在目标函数中增加惩罚函数,建立考虑系统可靠性约束的目标函数为:

式中:Ude为电网节点电压裕度约束;mmax和mmin分别为超于电压上下限的数量;Umax和Umin分别为节点电压裕度上下限;minPall_loss为损耗最小值;M为惩罚因子。
2.5 基于GA的最优潮流算法流程
GA 最早源于Darwin 的生物进化理论,是一种自然选择机制。其定义为:假设在某一特定的环境下,生物个体出于环境限制,采用生存竞争、适者生存的方式来遗传优良性状。
GA 主要包括编码、选择、交叉、变异等。在进行编码时需要确定编码的方式:通常情况下离散型变量采用二进制编码;连续型变量采用浮点数编码。选择主要包括轮盘赌、小生境技术等操作。交叉和变异主要通过设定值和位置进行操作。
将GA 应用到电力系统的方式为:在某一工况下通过设定初始值及约束条件,采用适应度函数来评价结果的优劣性。较劣的解被放弃,较优的解被遗传至下一代,直至获得最优解。
基于GA 的最优潮流流程图如图3 所示。

图3 基于GA的最优潮流流程图Fig.3 Flow chart of optimal power based on genetic algorithm
图3 的流程中几个重点步骤具体分析如下:
1)系统数据、GA 数据初始化。系统数据初始化,设定负荷节点功率大小及MMC 控制策略;遗传算法数据初始化,设定二进制编码方式及算法迭代次数,优化变量个数等。
2)换流器赋值。采用初始种群对换流器功率进行赋值,对主换流器输出的无功功率、从换流器输出的有功功率和无功功率采用交替迭代法进行系统潮流计算,并得到个体适应度值。
3)选择,交叉,变异。选择,为避免GA 陷入局部最优解,保证个体选择公平,采用轮盘赌的方法比较个体适应度;交叉,设定参数“交叉率”,提高后代适应度值;变异,设定参数“变异率”,通过修改染色体上随机位置的1 个基因实现变异。
4)换流器再次赋值。使用GA 得到的修订值再次对换流器功率指令值赋值,采用改进交替迭代法再次计算系统网损并求取最小值,与上1 次计算的网损最小值结果进行比较,选取全局最优值。
3 算例分析
为验证基于B2B-MMC 的柔性互联变电站优化调度方法的有效性,本文对某地实际配电进行改进,在其基础上增加了2 组B2B-MMC 系统,建立了含柔性互联变电站的配电网模型,该系统为11 节点系统,如图4 所示。
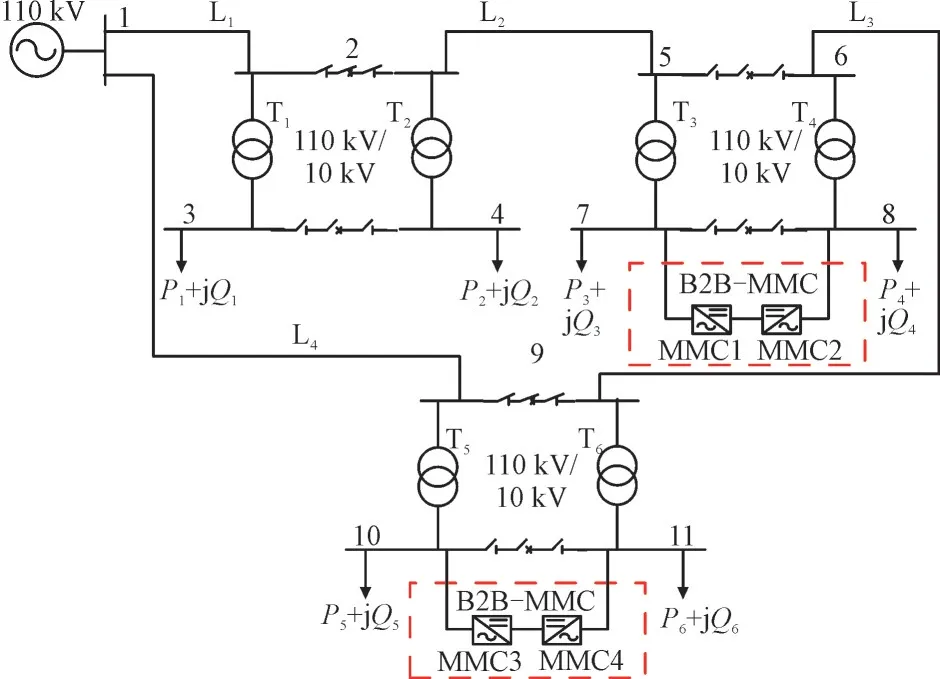
图4 含柔性互联变电站的配电网模型Fig.4 Model of distribution network with flexible interconnected substations
图4 中,1~11 为系统节点,线路电压等级为110 kV,线路型号选取LGJ—185,交流电源1 个,MMC1,MMC3 分别采用定直流电压控制和定无功功率控制,MMC2,MMC4 分别采用定有功功率控制和定无功功率控制,L1~L4为交流输电线路,T1~T6为6 台主变压器(其容量分别为40 MVA,31.5 MVA,31.5 MVA,40 MVA,50 MVA,40 MVA),P1+jQ1~P6+jQ6为10 kV 母线等效负载,以节点5 与节点6之间的母线为电网开环运行点;将变压器10 kV 母线负荷进行等效,节点负荷参数如表2 所示。

表2 节点负荷参数Table 2 Parameters of node load
本文利用GA 和改进改进交替迭代法对所建含柔性互联变电站的配电模型进行求解,并在目标函数中增加节点电压越限惩罚项,其惩罚因子取10 000,防止节点电压偏离电压设定的区间;GA 的参数设置为:种群规模100,进化代数50,交叉概率0.8,变异概率0.05,优化模型求解迭代过程中采用改进交替迭代法,迭代次数对应目标函数值如图5所示。
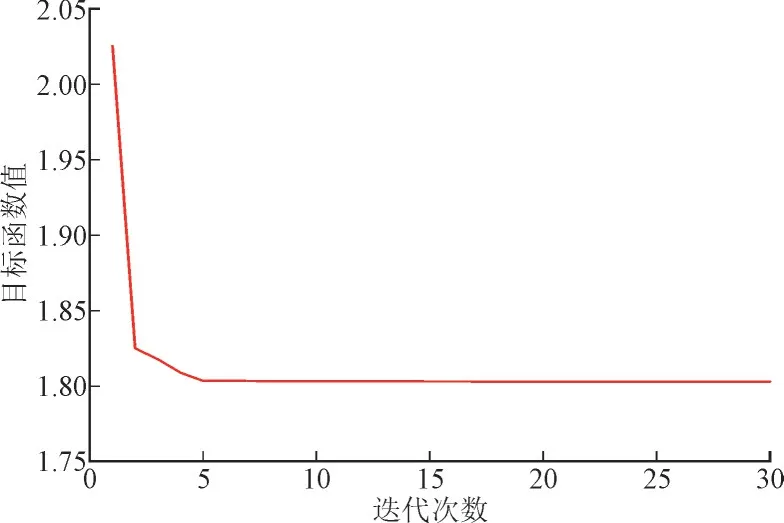
图5 迭代次数对应目标函数值Fig.5 The number of iterations corresponding to objective function value
由图5 可知,GA 在迭代5 次后趋于稳定,在迭代到第7 次时目标函数值发生微小变化。说明该算法能朝着最优解移动。输出目标函数值的同时得到换流器功率指令值的优化调度值,换流器功率输出值如表3 所示,优化值中+,-表示换流器功率的流入、流出。

表3 换流器功率输出值Table 3 Power output value of converter
优化前后节点电压对比图如图6 所示。由图6可知,所提方法在有效地降低系统网损的同时改善了配电网电压质量。优化前网损为2.196 MW,优化后的损耗主要由2 部分组成:网络损耗为1.588 MW,换流器损耗约为0.215 MW。与优化前相比网损降低了17.8%,电压偏差改善了5.2%,有效提升了电网的运行潜力,体现了柔性互联变电站在配电网中应用的优势。
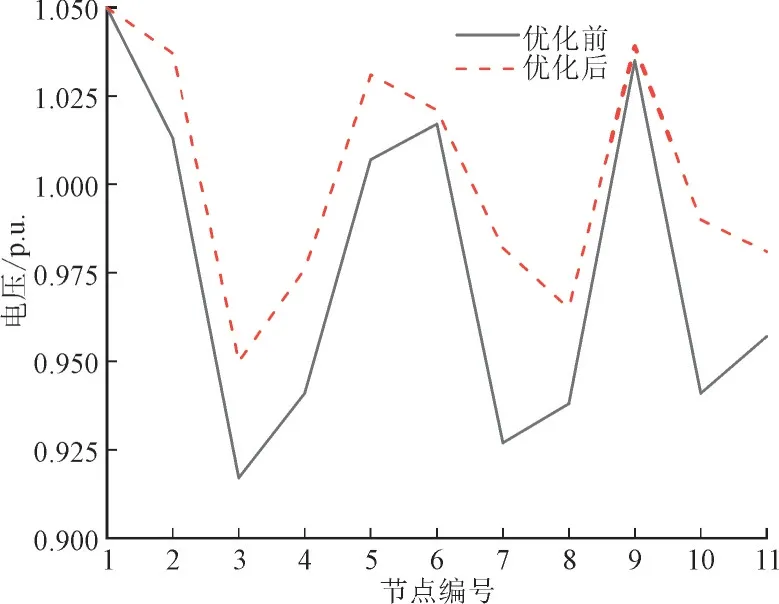
图6 节点电压对比图Fig.6 Comparison of node voltage
4 结论
本文提出一种基于B2B-MMC 的柔性互联变电站的优化调度方法,通过算例分析验证得到以下结论:
1)柔性互联变电站架构的提出,为电网提供多种灵活的运行方式,实现电网区域自治优化。
2)实现多个变电站间的协调互动及系统潮流的主动调控,有效降低了网络损耗,较未优化前损耗降低17.8%,缩小了电网节点电压范围。
本文所提调度方法仅考虑单一时间尺度下柔性互联变电站对电网的改善效果,后续将研究增加风光预测曲线,多时间尺度下换流器的输出功率对电网的优化效果,以及下垂控制、多个B2B-MMC 换流器下对系统优化结果的影响。
