基于多尺度并行卡尔曼滤波算法的电池状态参数估算

孔德昊 刘胜永

摘   要：准确估算并合理利用电池的荷电状态（state of charge，SOC）与健康状态（state of health，SOH）可以延长电池的使用寿命。为了实现准确的SOC-SOH在线估计，在扩展卡爾曼滤波的基础上，采用多尺度并行扩展卡尔曼滤波估计算法（multi-scale double extended Kalman filter，MDEKF）提高估计精度。在建立电池2阶RC等效电路模型上，利用最小二乘法对模型参数进行辨识，设计并行结构的滤波器进行电池SOC估计和参数修正，并以电池组容量值作为表征量对SOH进行估算。仿真实验结果表明，SOC估计误差由1.43%降低到1.10%，SOH估计结果稳定在0.5%以内，验证了算法的快速收敛性和实时性。

关键词：SOC-SOH估计;多尺度并行扩展卡尔曼滤波;2阶RC等效模型

中图分类号：TM912         DOI：10.16375/j.cnki.cn45-1395/t.2022.02.008

0    引言

电池参数SOC和SOH是描述电池状态的两个关键参数，二者之间存在紧密联系。在对SOC进行单独估计时，若电池SOH已经产生偏移，会使得SOC估计产生较大误差。所以，对二者进行准确的估计可以保证电池能够合理的充放电，从而延长电池的寿命[1-2]。

国内外早期对SOC的估计方法有开路电压法和安时积分法，前者需要测量静止电压，缺乏实时性;后者容易在积分过程中累计误差，造成结果发散。文献[3]用模糊规则优化算法改进神经网络结构的方法，完成了对SOC的估计。但神经网络算法离不开大量实验数据的支持，并且训练方法也会对运算速度和结果精度产生较大的影响，所以通过建立电池等效模型对SOC进行估算逐渐成为研究主流。文献[4]通过建立SOC与开路电压、电池模型参数的关系，提出自适应无迹卡尔曼滤波算法。文献[5]引用噪声自适应因子，利用平方根球形无迹卡尔曼滤波算法完成对SOC的估算。文献[6]提出了自适应无迹卡尔曼滤波算法和H无穷滤波算法相结合的方法对电池状态和参数联合估计，实验结果表明该方法有更好的鲁棒性。文献[7]采用自适应无迹卡尔曼滤波算法对列车蓄电池在实际工况下的SOC-SOH进行估算。但是，以上研究均忽略了当SOC初始值存在误差时对估算结果的影响。文献[8]证明了双扩展卡尔曼滤波算法估计SOC的可行性，在SOC初值存在误差的情况下，估计结果也可较好收敛于估计值，但论文未对SOH的估算进行讨论。

针对以上问题，本文提出采用并行扩展卡尔曼算法进行SOC-SOH联合估算，通过MDEKF算法对电池组SOC和模型参数同时进行估计，将电池组容量作为表征参数，通过实时的容量参数值求得相对应的SOH，在UDDS工况下验证SOC-SOH的在线估计，达到了预期的误差精度要求，解决了卡尔曼滤波无法同时估算SOC、SOH的问题，并提高了估算精度。

1    电池模型

1.1   等效电路模型建立

文献[9]表明，等效电路模型能够准确地反映电池的物理变化和化学变化，且计算量低，可以成功应用于电池SOC与SOH的估算。故本文采用2阶RC电路模型，如图1所示。

图1中：[Uocv、Uout]为开路电压和端电压，[I]为电池工作电流，[R0]为欧姆内阻，[C1、R1、U1]为电化学极化电容、电阻和电压，[C2、R2、U2]为浓度极化电容、电阻和电压。

根据基尔霍夫定律得到系统方程和观测方程。定义放电电流方向为正，充电电流方向为负。

系统方程：

[dU1dt=-1R1C1U1+1C1I，dU2dt=-1R2C2U2+1C2I，dSSOCdt=-1QnI.]            （1）

观测方程：

[Uout=Uocv（SSOC）-R0I-U1-U2]   ，         （2）

式中：[Qn]为电池的标称容量，[SSOC]为电池SOC     的值。

将式（1）进行在k时刻的离散化并化简得到：

[xk=Axk-1+BIT， k，yk=Cxk+DIT， k+Uocv（SSOC）.]         （3）

其中：[x=U1， U2， SSOCT]，[y=Uout]，

[A=1-TsR1C10001-TsR1C10001]，[B=TsC1TsC2-TsQn]，

[C=[-1， -1， 0]]，[D=-R0]，k表示时刻k中每个变量的值;[Ts]代表采样周期，是从k时刻到k+1时刻的时间，是常量值;[IT， k]表示k时刻的电池工作电流。

1.2   模型参数辨识

采用最小二乘法[10]识别式（1）和式（2）中电池的未知参数[R0]、[R1]、[R2]、[C1]、[C2]和非线性函数[Uocv（SSOC）]。选取三星公司生产的INR18650-30Q锂离子电池，10个电池并联成电池组作为研究对象，实验平台为ITECH公司生产的ITS5300电池充放电测试系统（ITS 5300 Battery Test System）。电池基本参数：标称容量为3 000 mA·h，标称电压为3.6 V，放电截止电压为2.5 V，充电截止电压为4.2 V。对电池进行恒流脉冲放电实验，实验中电池端电压曲线图如图2（a）和图2（b）所示，将安时积分法所得值设为端电压真实值，相对比得到端电压模型值与真实值误差如图2（c）所示。由图2可以看出，两者误差值基本稳定在±0.05%以内，模型准确，可以进行电池模型参数辨识。

1.2.1    电池欧姆内阻辨识

参数辨识的原理取决于电池的物理行为。根据图2可知，一旦放电电流执行或停止，端电压立即下降或上升，因为电容器[C1]、[C2]的电压[U1]、[U2]在開始放电时不会突然改变，所以欧姆内阻[R0]可以通过开始/结束放电时端电压的变化来确定。在图2中选取一个放电周期，选取[ta]、[tb]、[tc]、[td]时间点的端电压，可以计算欧姆内阻[R0]：

[R0=|VT（tb）-VT（ta）|+|VT（td）-VT（tc）|2|I|].      （4）

1.2.2     电池极化电阻和极化电容辨识

参数[R1]、[R2]、[C1]、[C2]的识别分为两步：第一步确定时间常数[τ1]、[τ2];第二步识别参数[R1]、[R2]、[C1]、[C2]，给出公式用以辨识极化电阻和极化电容：

[U（t）=U（t0）e-t-t0τ+IR（1-e-t-t0τ）]  ，         （5）

式中：[τ=RC]，[t0]为松弛过程的初始时间。

通过使用MATLAB函数“自定义方程”在曲线拟合工具箱，确定了时间常数[τ];通过式（7）确定[U1（tc）]、[U2（tc）]。参数求解公式如下：

[R1=U1（tc）I（1-e-tc-taτ1），R2=U2（tc）I（1-e-tc-taτ2），C1=τ1R1，C2=τ2R2.]                       （6）

电池参数辨识完成，结果如表1所示。

1.3    OCV-SOC曲线实验标定

采用曲线拟合的方法对非线性函数OCV-SOC进行辨识[11]，通过间歇恒流脉冲放电实验并将电池在放电结束后静置2 h，确保松弛过程结束。为了准确地拟合测量数据，采用6阶多项式：

[Uovc（SSOC）=4.723 6S6SOC-10.556S5SOC+3.877 1S4SOC+7.131 5S3SOC-7.695 9S2SOC+]

[3.802 4S1SOC+2.869 1.]                                    （7）

该多项式的拟合结果图如图3所示。

1.4   扩展卡尔曼滤波算法

卡尔曼滤波[12]是一种高效率的递归滤波器，能够从一系列不完全包含噪声的测量中估计动态系统的状态，其适用范围为线性系统。在非线性系统中，通常采用扩展卡尔曼滤波（EKF）[13-14]，EKF的基本思想是将非线性系统线性化。对非线性函数的Taylor展开式进行1阶线性化阶段，忽略其余高阶项，从而将问题转化为线性。

EKF算法在估算电池状态时有很大的局限性。电池在使用的过程中，电池内部的锂离子活跃性会逐渐变差，电池寿命会随着参与化学反应的锂离子数目减少而逐渐衰减。等效电路模型是根据电池内部的电化学反应而建立，当电池老化时，电池内部电化学反应程度发生变化，导致电池模型参数产生相应的改变。EKF算法在估算电池状态时将电池内部参数当作定值，使得估计结果会有较大误差。

随着电池的使用，电池老化不可避免。由于电池老化产生的电池内部参数改变会导致估计结果产生较大的偏差，为了最大程度地减小此类偏差产生的影响，在EKF算法的基础上进行改进，让等效电路模型参数进行在线自我调节，使电池模型更加贴合真实情况下的电池，在保证模型的基础上提高估计精度。

2    MDEKF算法的实现

提出多尺度并行扩展卡尔曼算法（MDEKF）对电池状态和参数进行估计。该算法将设计2个并行的扩展卡尔曼滤波器（EKF）分别用于状态滤波和参数滤波。考虑到电池内部参数随时间改变程度较小，在多尺度的构想下分别对2个滤波器设定不同的采样时间，以便达到减小计算量，使结果更加快速收敛的目的。

在电池模型建立中已经将电池模型进行了离散化处理，电池模型的状态和参数的空间方程如     式（8）—式（12）所示：

[dθdt=θk+1-θkTs]  ，                        （8）

[xk+1=F（xk， θk， Ik）=]

[1-TsR1C10001-TsR1C10001xx+TsC1TsC2-TsQnI+ωxk] ，  （9）

[θk+1=θk+ωθk]      ，                    （10）

[Uout， k=G（xk， θk， Ik）=Uocv（SSOCk）-U1-U2-R0I+υk] ，    （11）

[xk=[U1， k， U2， k， SSOCk]T，θk=[R0， k， R1， k， R2， k， C1， k， C2， k， Qk].]            （12）

其中：下标[k]表示变量在步骤[k]中的值;[Ts]、[ts]为2个时间尺度下的采样时间;[x]表示电池状态，[θ]表示所有电池模型需要迭代的参数，[ωxk]和[ωθk]是电池状态和参数在步骤k时的过程噪声，与电池状态和参数无关，它们的协方差矩阵分别为[Qx]和[Qθ]，与式（18）中的[Qk]不为同一变量;[ʋxk]和[ʋθk]是电池状态和参数在步骤[k]时的测量噪声，它们的协方差矩阵为[Rk]。

多尺度并行扩展卡尔曼滤波算法（MDEKF）就是同时运行状态滤波器和参数滤波器，在不同时间尺度下对电池状态和参数进行运算，用电池容量表征SOH，从而完成该算法对SOC-SOH的联合估算。算法实现结构如图4所示。

状态和参数的估计方程和具体实现步骤为：

Step 1  算法初始化，对[θ0、x0、Pθ0、Px0]赋初始值。实现途径见式（13）：

[Pθ0=E[（θ-θ0）（θ-θ0）T]， θ0=E[θ]，Px0=E[（x-x0）（x-x0）T]， x0=E[x].]   （13）

Step 2  计算参数滤波器的时间更新方程。参数濾波器的采样时间为[Ts=6 s]，步长[k∈1， 2， …， ∞]。时间更新方程见式（14）：

[P-θk=Pθk-1+Qθ， θ-k=θk-1].             （14）

Step 3  计算参数滤波器的测量更新方程。测量更新方程见式（15），得到[θk]后将该值传递给状态过滤器进行计算，在一个采样周期后，状态过滤器返回执行Step 2更新电池参数。

[Kθk=P-θk（Cθk）T[CθkP-θk（Cθk）T+Rk]-1，θk=θ-k+Kθk[Yk-G（xk， θ-k， Ik）]，Pθk=P-θk-P-θkKθkCθk.]      （15）

其中：[Cθk=∂G（xk， θk， Ik）∂θ|θ=θk].

Step 4  计算状态滤波器的时间更新方程。参数滤波器的采样时间为[ts=0.1 s]，步长[k∈1， 2， …， ∞]。时间更新方程见式（16）：

[x-k=F（xk-1， θ-k-1， Ik-1）]，[P-xk=Ak-1Pxk-1ATk-1+Qx]. （16）

其中：[Ak-1=∂F（x， θk-1， Ik-1）∂x|x=xk-1].

Step 5  计算状态滤波器的测量更新方程。测量更新方程见式（17），该式计算可得第k步的SOC，在一个采样周期后，状态过滤器返回执行Step 4。因为2个滤波器采样周期不同，当2个滤波器采样时间在宏观时间尺度上相等时，状态滤波器接受参数滤波器更新的参数[θk+1]，继续更新SOC。

[Kxk=P-xk（Cxk）T[CxkP-xk（Cxk）T+Rk]-1，xk=x-k+Kxk[Yk-G（xk， θ-k， Ik）]，Pxk=P-xk-P-xkKxkCxk.]     （17）

其中：[Cxk=∂G（x， θk， Ik）∂x|x=xk].

在Step 3中更新了电池参数，提取电池容量参数Q，对SOH进行估计。在Step 3运行结束后返回Step 2更新参数，重复该过程，提取容量Q并更新SOH估计值（[SSOH]）。[SSOH]估计公式如式（18）所示：

[SSOHk=QkQ0]  .                        （18）

上述步骤中，[θ0、x0、Pθ0、Px0]是算法的初始值，[θ0]可以由电池实验数据计算得到，[x0]是电池状态初值，[Pθ0、Px0]分别是参数滤波器和状态滤波器的初始系统参数协方差矩阵，表示每次迭代的交付误差。[Qx]和[Qθ]是过程噪声的协方差矩阵，表示模型参数的初始误差，[Rx]表示测量误差。因此，通过降低[Q]值，使模型对电池模型的精度提高;通过降低[R]值，使算法实测值更加准确。[K]为卡尔曼增益，右上角的“-”表示算法中变量的预估值，顶部标签“^”表示算法中变量的估计值。

如果状态观测器的[Qx]取值过小，算法将不再考虑端电压的实测值，此时算法近似于库伦计数法。当SOC初始值误差较大时，得到的结果无法收敛;若[Rx]取值过小，算法将完全依赖于实测值，此时算法近似于开路电压法，精度无法达到预期。对于参数过滤器来说，如果[Qθ]取值过小，算法将会认为初始电池参数的取值无限逼近真实值，将会使参数过滤器不再更新电池参数，使算法变为EKF;若[Rθ]取值过小，会使参数滤波更新范围变大，导致算法发散。所以为保证算法性能，[Qx]、[Rx]、[Qθ]、[Rθ]应取合适的值，具体取值思路及极端取值造成的影响参考文献[15]。本文取值为：

[Qx=10-600010-600010-6，Rx=1，Px=100010001，Qθ=diag（10-4， 10， 10-3， 10， 10-3， 10-3），Rθ=0.1，Pθ=diag（10-4， 10， 10-3， 10， 10-3， 10-2）.]    （19）

3    实验验证与分析

通过UDDS行驶工况对提出的MDEKF算法进行验证。将离线估计的SOC作为真实值，并用EKF算法与本算法作比较，验证算法精度与稳定性;将容量估算值作为表征量，估计出SOH，通过讨论SOH的估计值再次反证SOC估计的准确性，从而完成双扩展卡尔曼滤波的SOC-SOH估算。

图5是MDEKF算法和EKF算法的SOC估计结果，MDEKF算法和EKF算法的SOC初始值设为0.8。从图5中可以看出，2种算法都能在初始SOC不正确的情况下追踪真实SOC，MDEKF算法的SOC估计精度的平均误差控制在1.10%，比EKF算法的平均误差1.43%降低了0.33%，而最大误差也由EKF的2.68%降低至2.26%。由时间初始时间段可以看出，MDEKF算法和EKF算法都可以在SOC初始值错误的情况下，估计值收敛于真实值，而对算法的采样时间进行多尺度思想优化后，MDEKF算法的收敛速度远远高于EKF算法。2种估计算法的数值结果如表2所示。

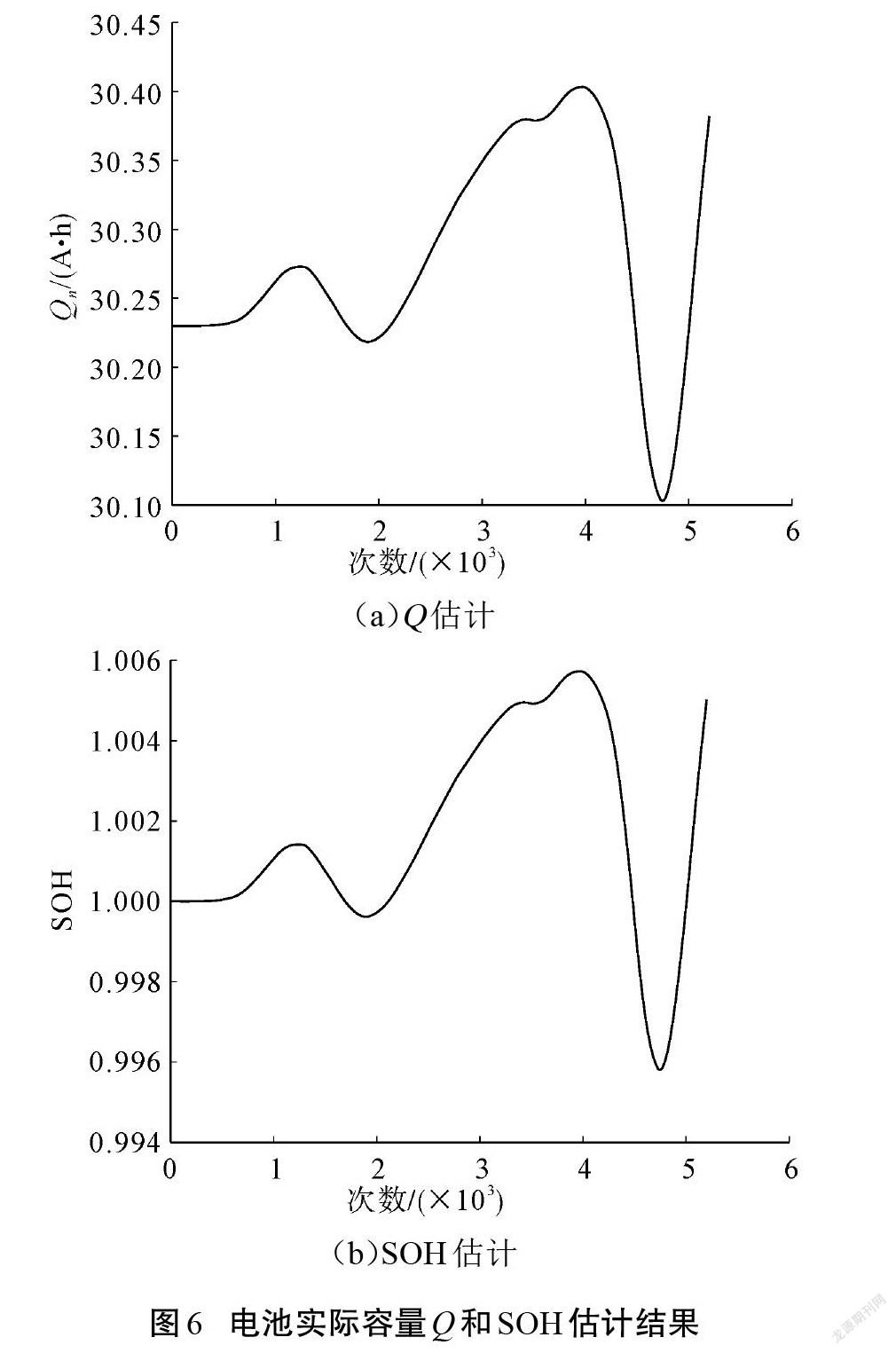
图6是在UDDS工况下采用MDEKF算法进行的电池实际容量[Q]估计和SOH估计。由于该工况时间周期较短，电池充放电次数还不足以使电池老化、出现额定容量下降的现象，所以默认在该工况运行中电池SOH真实值为1。由[Q]估计结果得知，电池在工况实验内估计容量值较好收敛于电池额定容量;SOH估计值相较于真实值，溢出偏移误差最大值为0.58%，亏损偏移误差为0.41%，估计结果总体误差不超过0.99%，由此证明了电池处于健康状态，验证了算法的预测性能准确。估计误差数值如表3所示。

4    結论

本文在2阶RC等效电路的基础上提出了多尺度并行扩展卡尔曼滤波算法（MDEKF），通过仿真测试验证算法的估计性能。结果表明，MDEKF算法可以实现SOC-SOH的联合估算，保证了估计精度，同时降低了运算量，使得SOC估计可以在初始值错误的情况下，能够快速作出反应并收敛于真实值，避免了因初始值错误而导致无法对电池状态进行估计。估计结果收敛后与EKF估计结果相比，平均误差由1.43%降低到1.10%。

参考文献

[1]     马华，从长杰，王驰伟.储能用锂离子动力电池研究进展[J].化学工业与工程，2014，31（3）：26-33.

[2]     孙道明.动力锂离子电池SOC和容量估计方法研究[D].杭州：浙江大学，2021.

[3]     钱建文，杜翀，田欣，等.一种改进T-S模糊神经网络估计锂电池SOC的方法[J].电源技术，2020，44（9）：1270-1273.

[4]     宫兵，凌六一，何业梁，等.基于自适应无迹卡尔曼滤波的锂电池SOC估计[J].电源技术，2020，44（11）：1594-1599.

[5]     刘楠，叶望博，李明，等.自适应平方根球型卡尔曼滤波下的SOC估计[J].电源技术，2021，45（2）：173-176，239.

[6]     王志福，李仁杰，李霞.基于混合AUKF和HIFF的锂离子电池SOC估计[J].电池，2021，51（4）：380-384.

[7]     郭佑民，戴银娟，付石磊.城轨车用复合动力储能系统蓄电池SOC和SOH估计[J].铁道科学与工程学报，2020，17（11）：2920-2928.

[8]     唐传雨，韩华春，史明明，等.基于DEKF的储能电池系统SOC估计方法研究[J].电力工程技术，2021，40（3）：7-14.

[9]     吴小慧，张兴敢.锂电池二阶RC等效电路模型参数辨识[J].南京大学学报（自然科学版），2020，56（5）：754-761.

[10]   陈息坤，孙冬.锂离子电池建模及其参数辨识方法研究[J].中国电机工程学报，2016，36（22）：6254-6261.

[11]   ZHENG F D，XING Y J，JIANG J C，et al.Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries[J].Applied Energy，2016，183：513-525.

[12]   彭丁聪.卡尔曼滤波的基本原理及应用[J].软件导刊，2009，8（11）：32-34.

[13]   万亚坤，李阳春，马浩天，等.基于扩展卡尔曼滤波算法的锂电池SOC估计[J].蓄电池，2020，57（5）：243-246，250.

[14]   王党树，王新霞.基于扩展卡尔曼滤波的锂电池SOC估算[J].电源技术，2019，43（9）：1458-1460.

[15]   ZHU Q，XIONG N，YANG M L，et al.State of charge estimation for lithium-ion battery based on nonlinear observer：an H∞ method[J].Energies，2017，10（5）：1-19.

Estimation of battery state parameters based on a multi-scale double extended Kalman filter algorithm

KONG Dehao1，LIU Shengyong*1，2

（1.School of Electrical， Electronic and Computer Science， Guangxi University of Science and Technology，

Liuzhou 545616， China; 2. Guangxi Key Laboratory of Automobile Components and Vehicle Technology（Guangxi University of Science and Technology）， Liuzhou 545006， China）

Abstract： Accurate estimation of state of charge （SOC） and state of health （SOH） of the battery and    rational utilization can extend its life. Multi-scale double extended Kalman filter （MDEKF） algorithm was adopted based on extended Kalman filter algorithm to improve the accuracy of SOC-SOH online estimation. Firstly， 2-RC equivalent circuit model was established. Secondly， the least square method was used to identify the model parameters. Then， a filter with double structures was designed to           estimate the battery SOC and modify the parameters， and battery SOH was estimated with battery pack capacity as representation. The simulation results verify the fast convergence and real-time performance of the algorithm. The SOC estimation error decreases from 1.43% to 1.10%， and the SOH estimation   result is stable within 0.5%.

Key words： SOC-SOH estimation; multi-scale double extended Kalman filter; 2-RC equivalent model

（責任编辑：黎  娅）