巨震下设置黏弹性阻尼RC框架结构抗倒塌分析

万黄晨 张敏

摘  要：为研究传统抗震结构设置黏弹性阻尼器对巨震作用的抗倒塌性能，采用增量动力分析（incremental dynamic analysis，IDA）方法，针对II类场地23条具有代表性的巨震波作用对结构楼层位移、能量耗散、结构倒塌的易损性曲线及结构塑性铰分布等分别进行动力弹塑性分析。工程算例分析表明：巨震作用下，设置黏弹性阻尼器的减震结构楼层最大位移和层间最大位移角均明显减小，其倒塌概率远低于相应传统抗震结构相应值，而抗倒塌安全储备系数明显高于相应抗震结构相应值;另外，减震结构塑性铰远未达到承载力丧失的程度，而抗震结构的塑性铰处于承载能力即将失效状态。由此表明，巨震作用下，黏弹性阻尼器减震结构相较于传统抗震结构能有效耗散地震能量，改善框架结构的屈服机制，增大结构抗倒塌安全储备，因而能显著提高结构抗倒塌性能。

关键词：巨震;黏弹性阻尼器;增量动力分析法;有限元结构模型;动力响应分析

中图分类号：TU352.1        DOI：10.16375/j.cnki.cn45-1395/t.2022.02.004

0    引言

近年来全球多地发生烈度巨大的地震，如汶川大地震以及“3·11”日本地震等，导致大量建筑倒塌。这些地震烈度较高，远超罕遇烈度地震的范畴，这种特大地震通常称为巨震。巨震及其引发的次生灾害造成了重大的人员伤亡和财产损失。如何防止或减弱巨震带来的损失已成为国内外学者关注的热点。

传统建筑结构主要是通过增大其承载能力或提高其弹塑性变形能力来抵抗大震的作用。然而在远超大震水平的巨震作用下，会引起结构较大损伤，甚至发生整体倒塌，如何保证巨震作用下结构不发生倒塌是众多学者关注的问题。结构振动控制是防震减灾的重要技术手段之一，由于黏弹性阻尼器构造简单，抗剪切稳定性高，微小的振动也能向被加固的结构提供阻尼，并可重复使用，较黏滞阻尼器和金属阻尼器性价比高[1]，因而得到越来越广泛的应用。能否通过设置黏弹性阻尼器自身变形耗散地震能量以确保结构在巨震作用下不发生倒塌，是一个值得研究的问题。

目前，众多学者针对传统建筑结构在巨震下产生的震害开展了研究。马玉虎等[2]在漩口中学巨震区同一场地选取10个RC框架进行震害考察，认为抗震目标应该由之前的“大震不倒”向“巨震不倒”转变。吕大刚等[3]提出由“三级水准设防原则”向“四级水准（巨震）设防原则”转变，并确定巨震设防风险导向的解析方法，通过指定目标下倒塌概率值计算得到巨震作用下的峰值地面加速度值，这为后续研究提供了理论依据。周云等[4]根据设置黏弹性阻尼器结构的性能特征和响应特点，提出以层间位移为控制函数，并按该函数优化布置阻尼器。李创第等[5-6]基于小震作用下研究了黏弹性阻尼器单自由度随机响应和多层基础隔震响应，并且简化了黏弹性阻尼器在地震激励下的求解过程。夏雨等[7]研究黏弹性阻尼器的支撑刚度与减震性能间的关系，结果表明黏弹性阻尼器支撑刚度与其减震性能呈正相关。张敏等[8]研究了在小震作用下设置黏弹性阻尼器框架的相关减震性能参数，认为阻尼器支撑刚度達到一定值时，阻尼器支撑基本不影响阻尼器对结构的减震性能，并在此基础上提出了计算设置黏弹性阻尼器框架地震作用的计算方法。

现阶段，大多数文献主要是对小震作用下设置黏弹性阻尼器结构的减震性能进行研究，而对于巨震作用下黏弹性阻尼器的减震性能研究相对较少。鉴于此，本文针对按抗震要求配筋的框架结构设置黏弹性阻尼器，在II类场地23条具有代表性的巨震波作用下，研究该结构能否实现“巨震不倒”的目标，并针对该结构进行巨震作用弹塑性动力响应分析，主要包括结构弹塑性层间位移分析、结构自身耗能分析、阻尼器耗能分析、结构易损性分析、以及结构塑性铰分布分析，进而研究结构设置黏弹性阻尼器框架在巨震作用下的抗倒塌性能。

1    基于IDA的易损性分析法

1.1   增量动力分析（IDA）的基本原理

增量动力分析 （incremental dynamic analysis，IDA） [9-10]是一种可以对结构进行精细定量分析的弹塑性研究方法，可对结构的地震易损性进行量化评估。IDA法将一组地震波按比例系数缩放后加载在结构上，通过逐步增加步长，得到结构的非线性时程响应，从而获得地震动强度指标（intensity measure，IM）和结构破坏指标（damage measure，DM）之间的关系，最后绘制成曲线，这条曲线即为IDA曲线。

1.2   地震波的选取

理论上选取地震波数量和种类越多，分析结果越精确，由此产生的工作量也会相应增加。因此，选取合理的地震波数量至关重要。黄炜元等[11]对中等高度的建筑进行增量动力分析研究，结果表明，取22条地震动记录可以满足较精确的地震分析需求。本文选取适用于Ⅱ类场地的4条人工地震波和19条实际观测记录的地震波，共计23条地震波。

1.3   地震动强度指标IM的选取

地震动强度指标主要有峰值地面加速度（peak ground acceleration，PGA）、峰值地面速度（peak ground velocity，PGV）、加速度反应谱（acceleration response spectrum，简称Sa（T1））等，为了与《建筑抗震设计规范》（GB 50011—2010）[12]中规定的设防烈度更好地对接，本文选用PGA作为地震动强度指标。根据文献[13]和表1中给出的建议值，选择超越概率为万年一遇的地震峰值加速度为巨震峰值加速度，见表1。故设防地震烈度为8度（0.30g）的巨震峰值加速度应为870 cm/s2。

表1    巨震峰值加速度建议值

[地震烈度 7度 7度

（0.15g） 8度 8度

（0.30g） 9度 PGA值 290 435 580 870 1 160 ]

1.4   结构破坏指标DM的选取

常用的DM指标主要有结构层间最大位移角、顶层位移、层间位移等，文献[14]详细分析了结构性能指标和地震动水平衡量指标对结构的影响以及选用建议。《建筑抗震设计规范》（GB 50011—2010）将弹性和弹塑性层间最大位移角[θmax]作为判定结构安全性能的指标。在巨震作用下，结构通常都会发生弹塑性变形，为了对接规范，本文以弹塑性层间最大位移角[θmax]作为结构倒塌破坏指标。根据《建筑抗震设计规范》（GB 50011—2010）规定，钢筋混凝土结构处于倒塌状态的弹塑性层间最大位移角[θmax]的临界值为1/50。

1.5   易损性分析步骤

基于IDA的易损性分析基本步骤如下：

Step 1  建立结构弹塑性分析模型。

Step 2  根据结构所在场地及震害信息，选用m条地震动记录与合适的IM指标。在某一地震波的IM指标下加载地震波，对混凝土框架结构分别进行弹塑性动力时程分析，若结构在给定IM指标下共有n条地震波的IM指标超过限定值，此时可认为在这n条地震波的作用下结构将发生倒塌，那么在该地震动强度下结构发生倒塌的概率为n/m，本文的m取23。

Step 3  由较低地震动强度指标固定步长逐步增大，重复Step 2，直到IM指标达到限值，得到该结构在不同IM指标下的DM指标。

Step 4  结构在选定IM指标下达到或超过给定临界值的概率，用超越概率[Pf]表示，其表达式    如下：

[Pf（μD≥μC/SIM）=φ（lnμD-lnμCβ2D+β2C）]，        （1）

式中：[φ（·）]为标准正态分布的累计概率函数，[SIM]为地震动强度指标值，[μD]为结构地震需求反应函数，[μC]为结构抗震能力概率函数， [μD]、[μC]分别为[μD]与[μC]的均值，[β2D]与[β2C]分别为[μD]与[μC]的对数标准差。根据文献[15]研究结论，[μD]与[μC]均服从对数正态分布，当以PGA为变量时，[β2D+β2C]取0.5。

ATC-63报告[16]中建议采用抗倒塌安全储备系数[σCMR]（collapse margin ration，CMR）作为量化评价结构抗倒塌能力大小的指标。汤保新等[17]将[σCMR]定义为50%倒塌概率的地震动强度指标值[SIM50%倒塌]与相应的结构设防大震的地震动强度指标值[SIM设防大震]之比，即：

[σCMR=SIM50%倒塌SIM设防大震] .                          （2）

2    有限元结构模型的建立

2.1   结构信息

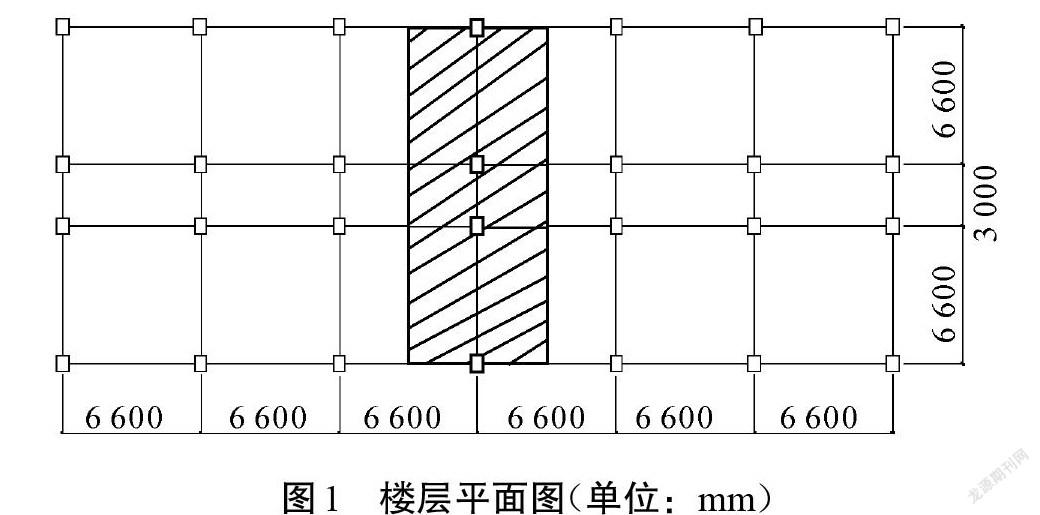
本文的工程算例为一栋10层钢筋框架结构。设计地震分组为第二组，Ⅱ类场地土，抗震设防烈度为8度（0.30g），设防类别为丙类，结构自身阻尼比为5%。本结构总高度为34.2 m，首层高度为     4.0 m，标准层高度为3.3 m;框架梁的截面尺寸均为[300  mm×600  mm]，框架梁的纵筋型号采用HRB400;柱子的截面尺寸均为[600  mm×750  mm]，柱子的受力纵筋型号采用HRB400;箍筋型号均采用HPB300。本结构梁柱均采用[C40]混凝土，屋面与各楼层恒荷载标准值均为[4.5] [kN/m2]，活荷载标准值均为[2.0] [kN/m2]，框架梁上墻体自重折算后的标准值为[3.2] [kN/m]。结构的平面如图1所示，分析一榀框架（计算单元如图1阴影所示），根据PKPM设计软件计算结构框架梁与柱配筋如图2所示，图中各数分别为结构梁柱单侧配筋面积，单位为[mm2]。

图2框架结构在各楼层设置黏弹性阻尼器以增强减震性能，防止巨震作用下上述框架结构发生 倒塌。

2.2   黏弹性阻尼器参数确定与布置方式

本文采用的黏弹性阻尼器是一种与阻尼器两端相对速度相关的平动式耗能器，采用Maxwell力学模型[18]来模拟黏弹性阻尼器。即一个弹簧单元与阻尼单元串联，如图3所示，该模型为理想状态下的Maxwell力学模型。

Maxwell的模型力学关系如下：

[dc（t）+dk（t）=d（t）]，                     （3）

[Kddk（t）=Cddc（t）=fd（t）].                （4）

经过傅里叶变换得：

[Dk（ω）+Dc（ω）=D（ω）]，                  （5）

[KdDk（ω）=iωCdDc（ω）=Fd（ω）]，            （6）

式中：[Cd]和[Kd]分别为黏弹性阻尼器的阻尼系数和弹簧单元刚度系数， [dc（t）]和[dk（t）]分别为阻尼单元和阻尼器弹簧单元的位移，[d（t）]为该阻尼器两端的相对位移，[fd（t）]为黏弹性阻尼器的阻尼力，[ω]为谐振的圆频率，[Dc（ω）]和[Dk（ω）]分别为[dc（t）和dk（t）]的傅里叶变换，[D（ω）]为[d（t）]的傅里叶变换，[Fd（ω）]为[fd（t）]的傅里叶变换。

令[Fd=K*（ω）D（ω）]，代入式（5）、式（6）中得到：

[K*（ω）=Cdηω2+iCdω1+η2ω2]，                     （7）

[η=CdKd].                                （8）

式中：[η]为[fd（t）]的松弛时间系数，[K*（ω）]为黏弹性阻尼器的复刚度，[i=-1]。相关研究表明，黏弹性阻尼器的抗震能力由松弛时间系数和阻尼器的阻尼系数共同决定，因此，选取合适的阻尼器参数对结构的抗震能力至关重要。根据文献[9]，本文各层阻尼器均取[η=0.1]，当阻尼器在各楼层水平设置时，各楼层阻尼器阻尼系数均取[Cd=5.0×107] N·s/m。

参照文献[19]，阻尼器宜在楼层连续布置，不宜间断，且宜在楼层平面对称分布。

阻尼器在实际工程中一般按楼层对角线方式倾斜安装。因此，本文采用SAP2000软件建模时阻尼器沿楼层对角线布置。根据力学原理，沿楼层对角线倾斜布置阻尼器的阻尼力与水平布置阻尼器的阻尼力的力学关系可按下列推导。

为了使阻尼器沿楼层对角线倾斜布置与水平布置达到同样的减震效果，阻尼器的阻尼力应满足下列关系。

当阻尼器水平布置时：

[Fd=Cd⋅u]，                       （9）

当阻尼器斜向布置时：

[Fd=Cd⋅（ucosθ）].                 （10）

假设结构水平振动，上述2种布置方式的阻尼力应满足下列要求：

[Fd=Fd⋅cosθ]，                  （11）

由式（9）—式（11）化简得：

[Cd=Cd（cosθ）2]，                     （12）

式中：[Fd、Fd]分别为水平式和斜撑式布置阻尼器的作用力，[u]为层间位移，[Cd、Cd]分别为水平式和斜撑式布置阻尼器的阻尼系数，[θ]为斜撑式布置阻尼器与水平楼面的夹角。

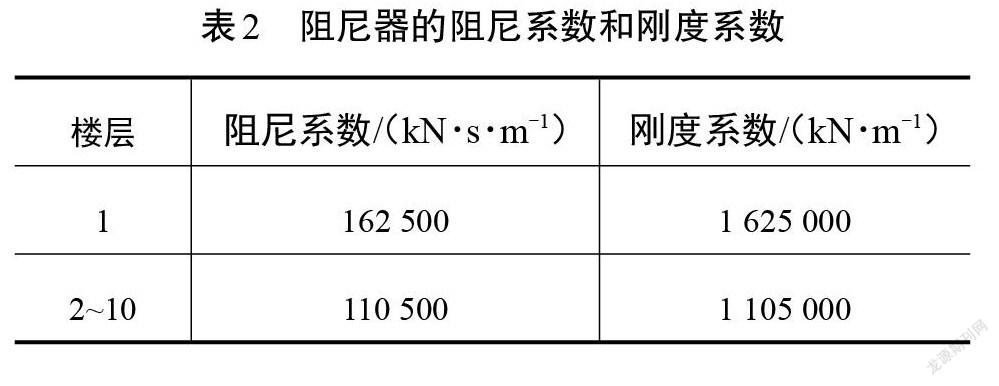
考虑第一楼层层高与其他楼层的区别，根据式（12），各楼层黏弹性阻尼器的阻尼器系数调整如 表2所示。

根据文献[19]及上述分析，本工程将各楼层阻尼器按图4连续布置在对角线上。

3    动力响应分析结果

3.1   楼层最大位移与层间最大位移角响应

采用SAP2000软件模拟传统无阻尼器抗震结构（简称抗震结构，下同）和设置黏弹性阻尼器的减震结构（简称减震结构，下同），分别在23条地震波作用下进行研究，计算抗震结构和减震结构的楼层最大位移和层间最大位移角响应，使用Matlab软件绘图。限于篇幅原因，仅列出El-Centro、PARKFIELD和RH2TG040这3条巨震波作用下的响应结果，分析表明其他20条地震波作用效果与上述3条地震波类似。

在巨震作用下，由图5和图6可看出，在设置黏弹性阻尼器后，減震结构楼层最大位移较抗震结构相应值显著减小，这在上部楼层表现尤其明显。结构的层间最大位移角均出现在结构底部。而抗震结构底层的层间最大位移角均接近甚至超过《建筑抗震设计规范》（GB 50011—2010）中弹塑性层间最大位移角，这表明传统抗震结构薄弱部位在结构首层，且在巨震作用时已经接近或者发生倒塌。对比之下，减震结构均未发生倒塌现象。相对于传统抗震结构，结构薄弱部位最大层间位移角降低均在50%以上，表明黏弹性阻尼器能够有效抵抗巨震作用，具有较强的减震性能。

3.2   结构能量分析

在巨震作用下，传统抗震结构依靠自身变形来耗散地震能量，而设置黏弹性阻尼器后框架结构通过阻尼器滞回变形以耗散地震能量。本文针对23条地震波，分别记录了抗震结构和减震结构在巨震作用下的能量。结构能量之间的关系见式（13）：

[EI=EH+EDP+EDC]，                    （13）

式中：[EI]为地震输入结构框架的总能量，[EH]为框架结构自身的总滞回耗能，[EDP]为阻尼器耗能，[EDC]为框架结构自身阻尼耗能。

由于各地震波持时不同，选取每条地震波单位时间内的耗能平均值，23条地震波作用下的结构能量分析见表3。由表3可知，在巨震作用下，地震输入减震结构与相应抗震结构的总能量相差无几。在减震结构中，黏弹性阻尼器消耗了大部分在抗震结构中本应该由结构自身耗散的能量，大大降低了结构自身的总滞回耗能，减少了弹塑性损伤，因此，减震结构的自身总阻尼器耗能（[ED]）与地震输入总能量之比[ED/EI]远大于传统抗震结构，表明减震结构有更好的抗震性能。

3.3   黏弹性阻尼器耗能分析

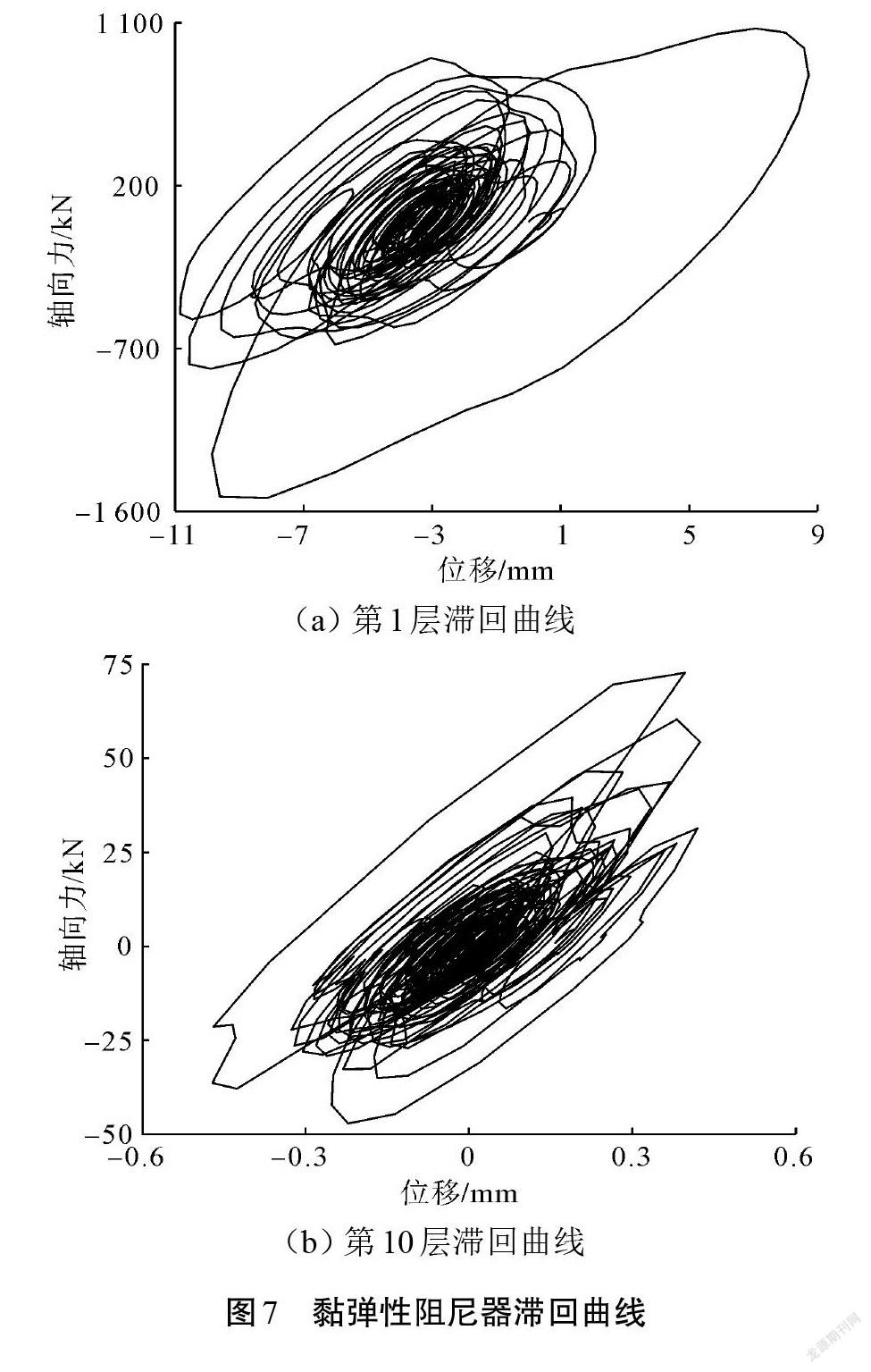
以El-Centro波（持时30.02 s）为例，经分析表明其他波作用下阻尼器滞回曲线及各楼层阻尼器耗能与El-Centro波类似。

图7和图8分别为El-Centro波作用下，第1层和第10层黏弹性阻尼器的滞回曲线及结构各楼层阻尼器的耗能分布曲线。从图7可见，黏弹性阻尼器的滞回曲线的形状比较饱满，呈现“梭形”，结构底层的滞回环面积较大，表明其在底层耗散了大部分地震输入结构的能量。由图8可知，黏弹性阻尼器在底层的滞回环曲线面积最大，阻尼器耗能由下部楼层到上部楼层依次减少，因而结构底部阻尼器耗能作用大于上部楼层。在巨震作用下，抗震结构底部弹塑性层间位移较大，因而底部受损伤程度较严重，设置黏弹性阻尼器能显著降低结构底部的损伤，提高结构的减震能力。

3.4   结构易损性分析

根据第1.5节步骤，使用SAP2000对减震结构和相应抗震结构分别进行非线性动力时程分析得到相关数据，导入式（1）可计算出减震结构和相应抗震结构的倒塌概率。研究表明地震反应函数和抗震概率函数呈现对数正态分布，将所得数据拟合成曲线，得到结构倒塌易损性曲线，如图9所示。由图9可知，按我国抗震规范设计的传统抗震框架结构，抵抗巨震作用的能力明显不足，巨震作用下，发生倒塌的概率较大，倒塌概率大概为48%。设置黏弹性阻尼器框架结构在巨震作用下的倒塌概率曲线随着地震动增大而缓慢上升，表明黏弹性阻尼器能有效降低结构在巨震作用下的弹塑性动力响应，在地震加速度0.87g处，倒塌概率很小，因而显著提高了结构巨震作用的抗倒塌性能。

据式（2）可计算出传统抗震结构和相应减震结构的抗倒塌储备系数[σCMR]，分别为1.80和3.14，可见在设置黏弹性阻尼器后，[σCMR]值明显增大，结构的抗倒塌性能得到了显著的提高。

3.5   结构塑性铰分布

在SAP2000中，通常使用自定義铰来模拟塑性变形后的结构性能。本文使用主方向的弯矩铰来模拟梁中间处产生的塑性铰，用剪力铰来模拟梁两端产生的塑性铰，使用PMM相关铰来模拟柱产生的塑性铰。图10为SAP2000软件中塑性铰力-位移曲线，A是起始点;B代表铰的屈服点，即弹塑性变形的临界点;C代表结构的承载力逐渐开始丧失;D代表残余强度;E代表构件完全失效。其中，超过B的塑性铰变形将被铰显现。根据SAP2000中文版使用指南[20]中规定：塑性铰的能力水平分别用点IO（立即使用）、LS（生命安全）、CP（防止倒塌）来表示，并分别用品红色、蓝色、青色、绿色、黄色来表示。

在巨震作用下，减震结构与相应抗震结构框架在El-Centro波作用下的塑性铰发展过程及分布情况如图11所示。由图11可知：1）地震刚开始时，塑性铰最先出现在结构底层的柱端，此时两结构均处于IO和LS状态，其中抗震结构首先出现塑性铰，发展较快，减震结构的塑性铰随后出现。2）随着地震波持续加载，传统抗震结构底层塑性铰很快出现承载力丧失的现象，结构出现较大变形，塑性铰由下往上快速发展。虽然减震结构在底层也出现了塑性铰，但基本处于IO和LS状态，远未进入失效状态。

通过分析发现，其他22条地震波在巨震作用下结构塑性铰发展与此波相似。

4    结论

通过分析一个10层框架结构工程案例，研究了黏弹性阻尼器减震结构与相应传统抗震结构在巨震作用下的动力响应，结论如下：

1）相比于传统抗震结构，设置黏弹性阻尼器的减震结构在最大层间位移、层间最大位移角、结构自身耗能上均表明其有着良好的抗震性能，显著增强了结构抵抗巨震作用的能力。

2）结构楼层设置的黏弹性阻尼器滞回曲线图形比较饱满，表明阻尼器耗能较大。在结构底部楼层耗能较大，表明黏弹性阻尼器显著降低了结构底部楼层的最大层间位移角，显著降低结构损伤，从而提高了结构抵抗巨震作用的能力。

3）在巨震作用下，减震结构的抗倒塌安全储备系数CMR值明显高于相应抗震结构CMR值，表明黏弹性阻尼器能大量耗散地震动输入结构的能量，显著提高减震结构在巨震下的抗倒塌安全性能。

4）抗震结构和减震结构在地震刚开始时在底层均出现塑性铰。随着时间的推移，抗震结构的塑性铰逐步向上扩展，而减震结构的塑性铰略微向上扩展，且均处于IO和LS状态，远没有到承载力丧失的程度，表明黏弹性阻尼器能有效减少结构的塑性变形，改善结构的屈服机制。

参考文献

[1]     张耀笑. 金属阻尼器与黏弹性阻尼器兼用的高层钢框架结构减震性能研究[D]. 镇江：江苏科技大学，2017.

[2]     马玉虎，陆新征，叶列平，等. 漩口中学典型框架结构震害模拟与分析[J]. 工程力学，2011，28（5）：71-77.

[3]     吕大刚，周洲，王丛，等. 考虑巨震的四级地震设防水平一致风险导向定义与决策分析[J]. 土木工程学报， 2018，51（11）：41-52.

[4]     周云，徐赵东，邓雪松. 黏弹性阻尼结构中阻尼器的优化设置[J]. 世界地震工程，1998，14（3）：3-5.

[5]     李创第，朱腾飞，柏大炼，等.实用黏弹性阻尼器耗能结构非平稳地震响应的快速求解[J].广西科技大学学报，2018，29（4）：13-20.

[6]     李创第，陶欣欣.设置粘弹阻尼器的基础隔震结构平稳响应分析[J].广西科技大学学报，2015，26（2）：20-25，30.

[7]     夏雨，李锦博，余颖烨.带支撑黏弹性阻尼器弱非线性耗能结构的随机地震响应分析[J].广西科技大学学报，2021，32（3）：21-26.

[8]     张敏，庞华英. 带支撑黏弹性阻尼器框架减震性能分析[J]. 应用力学学报， 2020，37（1）：418-426，498.

[9]     KIM J，LEE S，CHOI H. Progressive collapse resisting capacity of moment frames with viscous dampers[J]. The Structural Design of Tall and Special Buildings，2013，22（5）：399-414.

[10]   BAKER J W，CORNELL C A. A vector‐valued ground motion intensity measure consisting of spectral acceleration and epsilon[J]. Earthquake Engineering and Structural Dynamics，2005，34（10）：1193-1217.

[11]   黄炜元，张超，周云，等. 基于IDA的铅黏弹性阻尼减震结构地震易损性研究[J]. 土木与环境工程学报， 2021，43（3）：75-82.

[12]   中华人民共和国住房和城乡建设部. 建筑抗震设计规范：GB 50011—2010 [S]. 北京：中国建筑工业出版社， 2010.

[13]   姚攀峰，吕大刚. 结构工程中巨震峰值加速度的探讨[C]//中国土木工程学会. 第九届全国防震减灾工程学术研讨会论文集. 2016：41-51.

[14]   刘慧杰. 基于增量动力分析的RC框架结构地震易损性研究[D]. 西安：长安大学，2019.

[15]   VAMVATSIKOS D，CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics，2002，31（3）：491-514.

[16]   Federal Emergency Management Agency. Quantification of building seismic performance and factors：FEMA P695[R]. Washington DC，2009.

[17]   湯保新，叶列平，陆新征. 丙类与乙类设防RC框架结构抗地震倒塌能力对比[J]. 建筑结构学报，2011， 32（10）：30-38.

[18]   李创第，王博文，昌明静. 设置支撑的广义Maxwell阻尼耗能结构系统均匀与非均匀随机地震响应分析[J]. 桂林理工大学学报， 2020， 40（3）：523-529.

[19]   张敏，庞华英. 设置黏弹性阻尼耗能框架结构减震性能分析[J]. 计算力学学报，2019，36（6）：739-746.

[20]   北京金土木软件技术有限公司. SAP2000中文版使用指南[M]. 北京：人民交通出版社，2012.

Collapse resistance analysis of RC frame structure with viscoelastic damping under mega earthquake

WAN Huangchen1， ZHANG Min*1，2

（1. School of Civil Engineering， East China Jiaotong University， Nanchang 330013， China;

2. School of Civil Engineering， Jiangxi Science and Technology Normal University， Nanchang 330000， China）

Abstract： The collapse resistance of frame structure with viscoelastic dampers is studied. For the frame structure subjected from 23 representative mega earthquake waves in the class II site， the incremental dynamic analysis method is used for dynamic elastoplastic study of the floor displacement， energy     dissipation， collapse vulnerability curve and distribution of structural plastic hinge. The analysis of     engineering example shows that the floor displacement and the story layer angle of the damping     structure with viscoelastic dampers are obviously reduced under the mega earthquake， the collapse  probability is much lower than the corresponding value of the traditional frame structure without       viscoelastic damper， but the safety reserve coefficient of collapse resistance is obviously higher than the corresponding value of the traditional structure. In addition， the plastic hinges of the damping structure are far from bearing capacity loss， but the plastic hinges of the traditional frame structure are in the state of bearing capacity failure. From this， the viscoelastic damper structure can effectively dissipate the seismic energy， improve the yield mechanism of the frame structure， and increase the structural collapse resistance safety reserve， so the viscoelastic dampers can significantly improve the collapse resistance performance of the structure.

Key words： mega earthquake; viscoelastic damper; incremental dynamic analysis; finite element    structural model; dynamic response analysis

（责任编辑：罗小芬）