小学数学教师“问题提出”课堂教学行为研究
2022-04-11张莎莎宋乃庆蔡金法
张莎莎,宋乃庆,蔡金法
小学数学教师“问题提出”课堂教学行为研究
张莎莎1,宋乃庆1,2,蔡金法3
(1.西南大学 数学与统计学院,重庆 400715;2.西南大学 教育学部,重庆 400715;3.美国特拉华大学 数学系,纽瓦克 19716)
基于课堂教学视频的分析,以参加重庆小学数学“问题提出”教学工作坊不同学习阶段的6名教师为对象,从问题提出教学任务的设置、处理学生提出的数学问题两个方面分析小学数学教师的问题提出课堂教学行为.研究发现,除一位教师外,5位小学数学教师在参加问题提出教学工作坊后基本上能够顺利实施问题提出教学.小学数学教师选择的问题提出教学内容领域、执行任务所用的引导语及选取学生提出的问题方面具有较强的相似性;参加工作坊学习时间较长的教师在课堂教学中设置的问题提出任务数量、情境类型比学习时间较短的教师更加丰富,为学生提供了更多的学习机会,在处理学生提出的问题时更为灵活.这些研究结果进一步说明工作坊对于帮助小学数学教师进行问题提出教学的有效性.
小学数学教师;问题提出;课堂教学行为
1 问题提出
当今世界综合国力的竞争实质上是科技创新能力的竞争,创新型人才的培养已成为人类共同面临的重大课题.进入新时代,中国正在加快向创新型国家前列迈进,对教育发展提出了新的要求——培养大批符合时代发展需求的拔尖创新型人才.创新型人才的培养要靠教育,要靠改革现有的教育内容、教育思想和教育方法来实现[1].当前中国学生最缺乏的创新人才的基本素质是好奇心、想象力和批判性思维[2],让学生学会提问题有助于其好奇心、想象力和批判性思维的发展[3].爱因斯坦曾言:“提出一个问题往往比解决一个问题更重要,因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题、新的可能性、从新的角度去看旧的问题,需要有创造性的想象力,而且标志着科学的真正进步.”[4]中国著名教育家顾明远先生也说道:“不会提问的学生不是学习好的学生.”[5]“学会提问”是学生进行思考,展开深度学习的基本功,是导向新发现的转折点,是提高学生“自己即学习的主人”的意识的重要环节[6].问题提出(problem posing)长期被认为是至关重要的智力活动,是数学创造的一种形式,能够激发学生的创造性思维[7].此外,问题提出为学生提供了更多的学习机会,还可以作为透视学生思维和概念理解的窗口,促进学生问题提出、问题解决及非认知能力的发展[8].
自1989年美国数学课程标准中明确提出要给学生提出数学问题的机会[9],问题提出开始被数学教育研究者作为独立的研究对象,理论研究到实践研究日益丰富[10],涵盖了数学教材中问题提出任务分析、学生及教师问题提出能力的评估、问题提出与问题解决及非认知能力的关系探索、问题提出数学教学实践课例开发等研究领域.然而,尽管不同国家的数学课程标准一再强调问题提出[11–12],数学教材中的问题提出活动比例只占很小一部分,且主要分布在“数与代数”领域[13–14].如此对教材中问题提出的随意支持,使得教师难以在实际课堂中承担实施问题提出教学的重要工作,教师在课堂上很少给学生创设问题提出的机会.为帮助中国小学数学教师学习如何通过提出数学问题来教数学,在重庆、北京、杭州等地开展了一系列小学数学“问题提出”教学工作坊,由一位在问题提出和教师教育领域具有丰富研究经验的学者进行顶层设计,基于现有的数学教材内容,重点是如何设计问题提出任务并通过问题提出来教授数学[15].已有研究发现,经过工作坊主题式培训,小学数学教师的问题提出能力有所提高[16],在一定程度上转变了问题提出教学信念,提升了课堂教学能力[17–18],积累了成功的问题提出教学案例,呈现了数学课堂中问题提出教学的概貌[19].然而,目前还未有研究直接详细描述问题提出课堂教学实践现状,对于教师在问题提出数学课堂教学中需要怎样的支持是十分缺乏的.鉴于此,利用重庆小学数学问题提出教学工作坊提供的研究对象和实践基础,基于课堂教学视频分析的视角,分析参加工作坊不同学习阶段的6名小学数学教师的问题提出课堂教学行为,管窥小学数学教师问题提出课堂教学行为实然样态,为改进问题提出教学实践、反馈培训效果、厘正培训内容提供参考和建议.
2 研究设计
2.1 研究对象
研究对象的选择为重庆市小学数学“问题提出”教学工作坊中的研修教师.小学数学“问题提出”教学工作坊两年内共连续开展了4期,每期持续3天时间.为保证学员的自主性、积极性和参与度,每一期学员的选拔均采用自下而上的方式,由学员自主报名参加.由于工作坊时间安排与教师工作时间有部分重叠,4期全部参加的学员共15名.限于篇幅,工作坊开展的具体情况另文有详细描述[20],此处不再赘述.
采用目的性随机抽样的方式,综合考虑了学校地理位置、性别、教龄、职称等背景变量,使研究对象更具代表性,同时遵从自愿原则,从15名学员中选取了3名教师作为研究对象.为便于更好地说明工作坊的培训效果,在仅参加第三期工作坊的40名学员中选择3名作为研究对象.将4期工作坊均参加的3名教师编号为A1、A2、A3;只参加一期工作坊的3名教师编号为B1、B2、B3.研究对象具体情况如表1所示.

表1 研究对象具体背景信息
2.2 课堂教学视频分析框架
课堂视频分析法是借助于教学录像的课堂观察方法,在帮助研究者捕获复杂的课堂教学行为和教师反思教学等方面具有独特的优势,其重点在于开发合适的编码工具.由于课堂教学行为通常是复杂的,有许多可以调查的显著特征,因此需要确定与数学问题提出最相关的课堂教学行为.许天来基于蔡金法提出的数学教学框架[21],提炼出数学问题提出教学的一个框架,如图1所示.
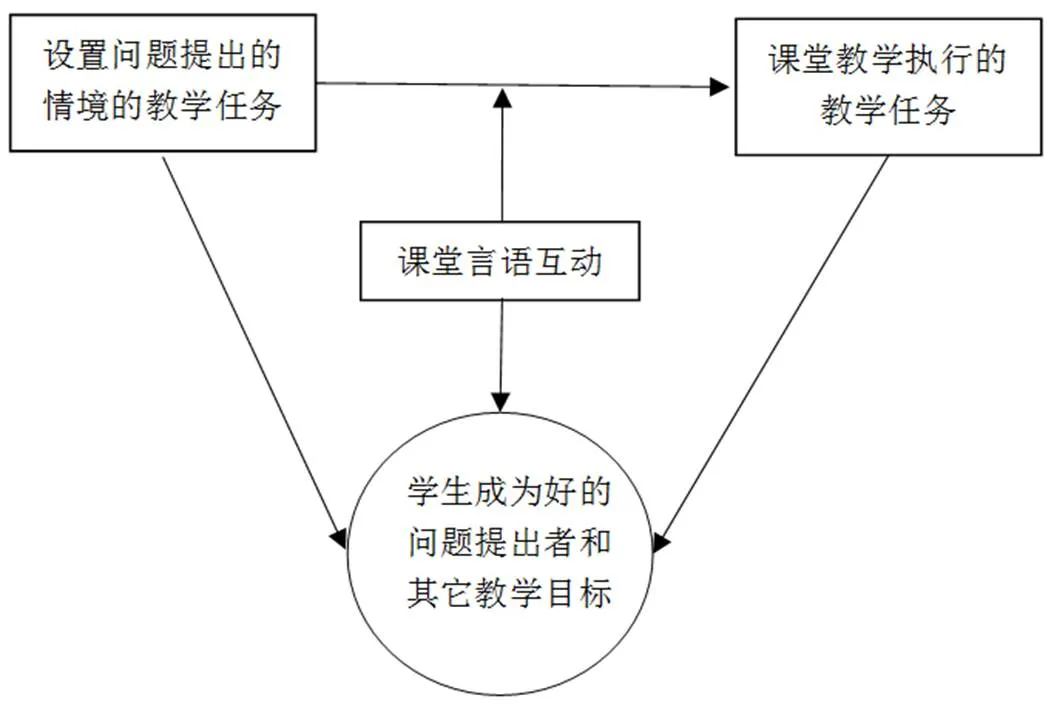
图1 数学问题提出教学的一个框架[24]
这一框架强调教师将问题提出作为教学目标和教学手段,合理设置问题提出情境的教学任务,师生通过课堂言语互动共同参与问题提出的过程,通过对这些教学任务的组织和实施,最终达成数学课程标准中关于问题提出的教学目标和其它教学目标.尽管这一框架未突显教师角色,但是“实际上,从确定学习目标、设计课堂言语互动,到选取合适的教学任务,这些都是由教师来完成的”[22].也就是说,在数学问题提出教学过程中教师行为起主导作用,学生行为、师生互动行为是由教师行为引发的,逻辑上不是并列关系.故此,将“教学行为”限定为“教师的教学行为”,但并未与学生的学习行为、师生互动行为相脱离,而是将之视为教师教学行为实施后的结果[23].
此外,有学者提出一般数学课堂教学中一个完整的问题提出活动通常要经历如下几个具体的教学过程:教师呈现问题提出情境(包括数学情境、现实情境、科学情境),教师给出“问题提出”任务的具体要求(对问题数量、难度或其它方面要求的引导语),学生提出问题、分析问题,教师或学生选取一个或多个问题最终解决问题[25].依据数学问题提出的教学框架及问题提出活动具体的教学过程,教师设置的问题提出教学任务以及处理学生提出的问题可以清楚地描绘出运用问题提出教授数学的过程.因此,研究重点关注教师设置问题提出教学任务及处理学生提出的数学问题两个主要教学行为方面.数学课堂教学始于教师设置的教学任务,教师选择和使用的任务是学生学习质量的主要决定因素.教学任务为学生的学习和数学思维的发展提供了智力环境,不仅控制学生对内容特定方面的注意力,而且控制他们处理信息的方式.由于并不是所有内容均适合问题提出教学,教师在教学中可能还会设置传统的问题解决任务,因此对教学任务的编码既包括问题提出任务,也包括问题解决任务.当问题提出用于课堂教学时,提示在问题提出任务中起着重要作用.有研究发现问题提出任务中的不同要求或提示会影响学生或教师的问题提出表现和问题提出过程[26],提示的含义部分取决于先前设置的任务的性质.因此,对设置的问题提出教学任务的要求(提示语)进行编码.教师如何处理学生提出的问题是以学生提出数学问题为前提的,是通过问题提出进行教学的一个重要方面.因此,首先需要对学生提出的数学问题进行编码.之后,再对教师处理学生提出的数学问题的方式进行编码,包括教师对学生提出的数学问题的关注程度,选择解决哪些问题,忽略哪些问题以及延迟关注哪些问题等.在初步拟定分析框架后征求问题提出领域研究相关专家意见,以形成正式的数学问题提出课堂教学行为编码与分析框架,如表2所示.
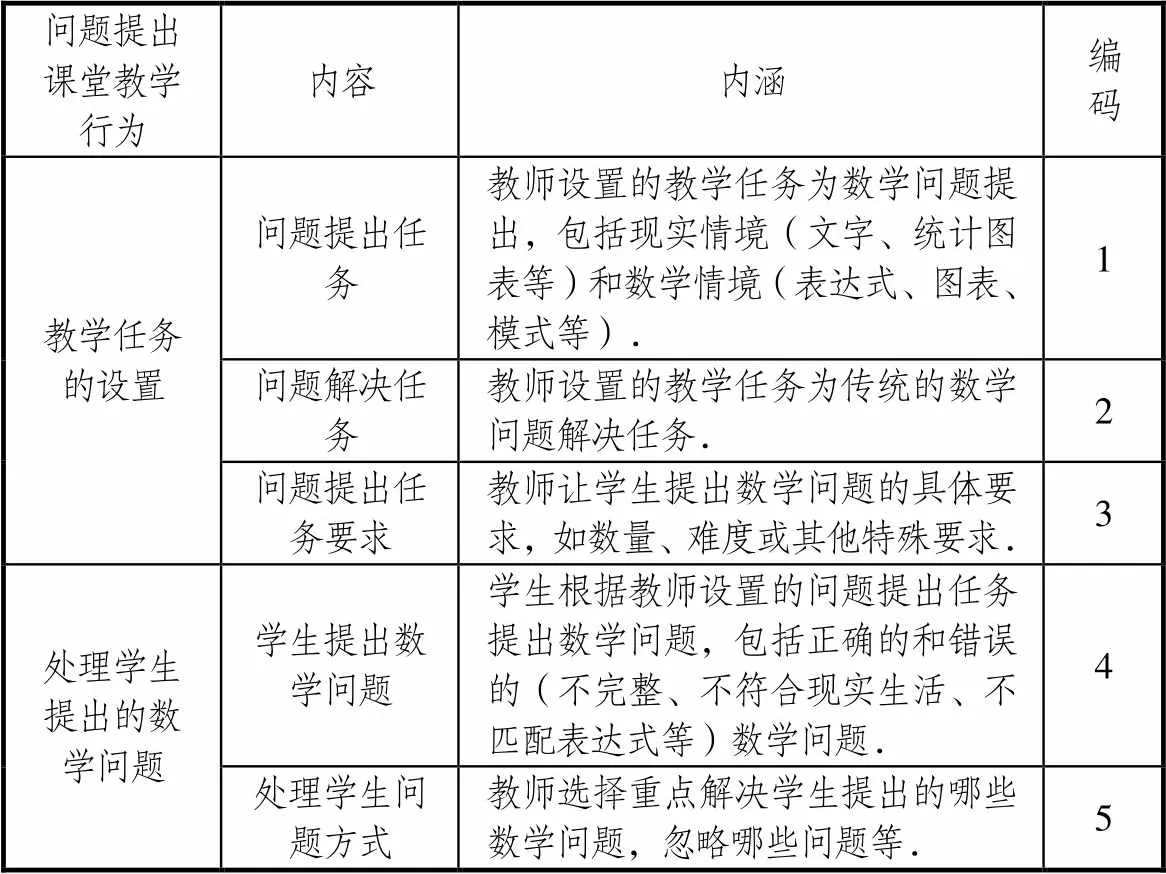
表2 问题提出课堂教学行为分析框架及编码
2.3 数据收集与编码
课堂教学视频于2020年秋季学期至2021年春季学期录制,距离2019年6月最后一次工作坊结束一年余的时间,为研究对象在课堂中尝试运用问题提出教学留出充足的时间.为遵守新冠肺炎疫情防控规定,最大限度地降低对被试正常教学秩序的影响,授课内容由研究对象自主选定,采用线上直播课及线下参与式观察的方式,运用录像设备记录课堂中发生的真实境况.采用质性分析软件NVivo 12 Plus进行编码与分析,首先将6位教师的课堂教学录像依次编号为VA1—VB3,逐一导入软件;然后,为便于回溯检查编码,以一个完整的话语结构为单位,在软件内容栏为课堂教学录像建立逐字稿;最后根据上述分析框架建立节点系统并对逐字稿进行编码,编码时由两名研究者独立进行,编码不一致之处通过讨论直到达成一致.
3 研究结果
研究结果分别从教师数学问题提出任务的设置和对学生提出的数学问题的处理两个方面进行呈现.
3.1 数学问题提出任务的设置
表3显示了6位教师所授课时的具体教学内容、时长、教学目标及课堂教学中设置的问题提出教学任务和问题解决教学任务数.可以看出,仅B1设置的课堂教学均为问题解决任务,没有涉及问题提出的教学任务,其余5位教师均设置了不同数量的问题提出任务,B1为何没有真正实施数学问题提出课堂教学将在后面部分进行细致讨论.可以发现,尽管录课时教材编排的教学内容涉及了“数与代数”“图形与几何”“统计与概率”不同的数学内容领域,然而,5位真正实施数学问题提出课堂教学的教师都不约而同地选择了“数与代数”领域开展问题提出教学,教学内容涉及不同年级且均为新授课.

表3 教师所授课时“内容”“时长”“教学目标”“教学任务数”
进一步分析各课例所设置的教学任务及其所在的教学环节、教学时间,如表4所示.可以看出,A组教师用于问题提出进行教学的时间均超过了10分钟,约占整节课的四分之一;而B组教师相对而言时间较少,尤其是B2仅用了不到3分钟的时间.5位小学教师在不同教学环节使用问题提出,除A2只在课堂练习环节运用问题提出开展教学,其余4位教师均将问题提出用于引入新课这一环节.5节课所设置的11个问题提出教学任务中,4个为现实生活情境,如A1设置的问题提出任务一;7个为纯数学情境,如A1设置的问题提出任务二.进一步分析两组教师创设的问题提出任务情境类型,可以看出B组教师设置的问题提出任务只有现实生活情境,A组教师设置的任务不仅有现实生活情境,且多为纯粹的数学情境.无论是生活情境还是数学情境,均是不同程度对现有教科书的改编而创设的,A组教师相对于B组教师的常规加工(将教科书中问题解决情境删去问题形成问题提出情境)而言,更擅长对教科书创造性加工以创设多样的问题提出任务情境.
教学任务是实现教学目标的重要支撑,针对同一个教学目标可以选择不同的教学任务.无论是问题提出任务还是问题解决任务,都应以教学目标为核心指向.这里根据课堂教学目标来审视教师设置的教学任务的合理性和有效性.A1设置的两个问题提出任务紧密围绕教学目标,且具有针对性和层次性:相较于教师直接给出问题让学生解决,任务一更能激发学生的求知欲,发展学生的问题提出能力,为学生创造更多交流表达的机会;相对于全班同学解决同一个问题,问题提出任务二能让学生积极主动地参与到数学活动中,不仅从整十数加减法自主迁移到整百数的加减法,进一步体验算法的多样化,而且每个学生都能根据自己的生活经验建构不同的数学问题,从而感受整百数加减法与生活的密切联系,同时进一步加深对加减法意义的理解,还为教师评估学生的理解提供重要路径.A2设置的两个问题提出任务指向3个教学目标,学生根据表达式编题不仅巩固了如何用字母表示数和数量关系,而且有助于理解“8”“+2”所蕴含的数量关系,在现实生活情境中唤起学生对字母表示数的理解,进一步理解用含有字母的式子表示两数之积、和或差的数量关系的普遍适用性,感受符号化思想.这种“逆向”的教学任务不仅激发了学生的学习兴趣,而且为学生提供了广阔的思维空间.而让学生根据数量关系的陈述写代数式,如教师设置的问题解决任务“1只手有5个手指,2只手有10个手指,只手有( )个手指”,仅能展现学生单方面的思维,削减了学生参与数学活动的机会.A3设置的3个问题提出任务主要针对教学目标1和目标3,和问题解决任务相比较而言,根据算式编数学问题能拓展学生的数学思维,而不仅限于“购物”这一情境,有助于学生在自己建构的生活情境中理解一位小数加减法的意义,感悟数学与生活的密切联系,提升解决简单的一位小数加减法实际问题的能力.B1虽然没有设计问题提出任务,但其课堂中的问题解决任务同样是围绕教学目标来设置的:通过任务一让学生经历梯形面积的推导过程,发展学生的空间观念和推理能力;任务二和任务三旨在让学生掌握计算方法,解决不同层次的实际问题.B2设置的教学任务主要指向教学目标1和目标3,让学生根据熟悉的情境提数学问题激发了学生的学习兴趣,能培养学生的问题提出能力和语言表达能力,学生解决自己提出的数学问题增强其学习的内驱力.B3设置的两个教学任务是为实现教学目标1和教学目标3而设计的,任务一根据现实情境提出数学问题,让学生主动投入到数学学习中,为不同学生提供不同的学习机会,让学生在实际情境中体会分数加减法的意义;任务二相对于常规的问题解决任务,能挖掘不同学习程度的学生的潜力,有助于学生掌握简单异分母分数加减法的计算方法,解决自己提出的实际问题,获得成就感.可以发现,教师设置的教学任务均指向教学目标,只是相对问题解决任务而言,同一教学目标下适宜地使用问题提出任务具有独特的优越性.

表4 各课例设置的教学任务具体信息
在数学问题提出任务中,引导语或者说对学生提出数学问题的要求是一个重要方面,不同的引导语对学生提出数学问题的思维过程及结果产生不同影响,例如“你能提出数学问题吗?”“你能尽可能多地提出数学问题吗?”“你能提出不同难度的数学问题吗?”3种不同层次的引导语,分别适用于学习基础较为薄弱、中等和优等的学生,能够为学生提供不同的学习机会.由表4可以看出,教师使用的引导语既有相似之处,又有差异.首先,相似之处体现在教师在引发学生提出数学问题时都使用了比较直接的措辞——“你能提出什么数学问题”.差异体现为两个根据表达式提出数学问题的任务,A1明确要求学生根据算式来编数学问题,对于低年级学生来说具有明确的指向性,有利于学生明白教师的意图,提出教师预设的指向教学目标的数学问题;A3要求学生尽可能多地提不同情境的数学问题,这是唯一一个鼓励学生尽可能多地提出数学问题的任务,有益于学生在具体情境中理解小数加减法,体会一位小数加减法与生活的密切联系,发展学生的量感,提升问题解决能力;B2对提问前提条件的强调(提问时用上3个已知条件),致使学生在提出数学问题时思维受限,学生能较快提出教师所预期的与教学目标密切相关的乘加、乘减数学问题.值得注意的是,尽管不同问题提出任务的引导语具有相似性,但由于情境类型的不同,实际对学生提出问题的要求是有所差异的.如“根据这3个算式0.8+0.6,0.8–0.6,1.2–0.6提问题”实际上是要求学生“提出与特定数学运算相匹配的数学问题”,而“妈妈买了一些毛线,给爸爸织毛衣用去了7/10,给红红织手套用去了1/20.你能提出什么数学问题并解答?”是要求学生“根据已知信息提出数学问题”,5位教师设置的所有问题提出任务只涉及这两类,并未涉及另外两种——“根据相同的数学结构提出不同的问题”“根据给定信息和示例问题提出额外的数学问题”.
3.2 对学生提出的数学问题的处理
由于教师选取的对象是学生提出的数学问题,首先对学生提出问题的总数和错误问题的数量进行编码和统计.如表5所示,总体而言,5节课中学生并未提出与学习内容无关的问题.学生提出的问题总数在一定程度上可以反映教师给学生的学习机会的多寡,A3教师执教的课例,学生提出问题数量最多(18个),B2教师最少(4个),并且其中两个为不正确的数学问题,这与其引导学生提问时使用的引导语有关.相对于B组教师而言,A组教师为学生创造了更多的学习机会.错误问题是指学生所提出的不是数学问题,或者提出的数学问题不完整,或不满足任务要求,或不符合现实生活情境,如A1的课例中,学生就任务二提出的“一班有900个皮球,二班有600个皮球,一共有多少个?”和B2的课例中学生提出的“买文具盒比买书包贵多少元?”被编码为不正确的数学问题,前者不符合生活实际,后者根据情境买书包要比买文具盒用的钱多.从错误问题数量来看,低年级学生相对高年级学生在提数学问题时似乎更容易出错.
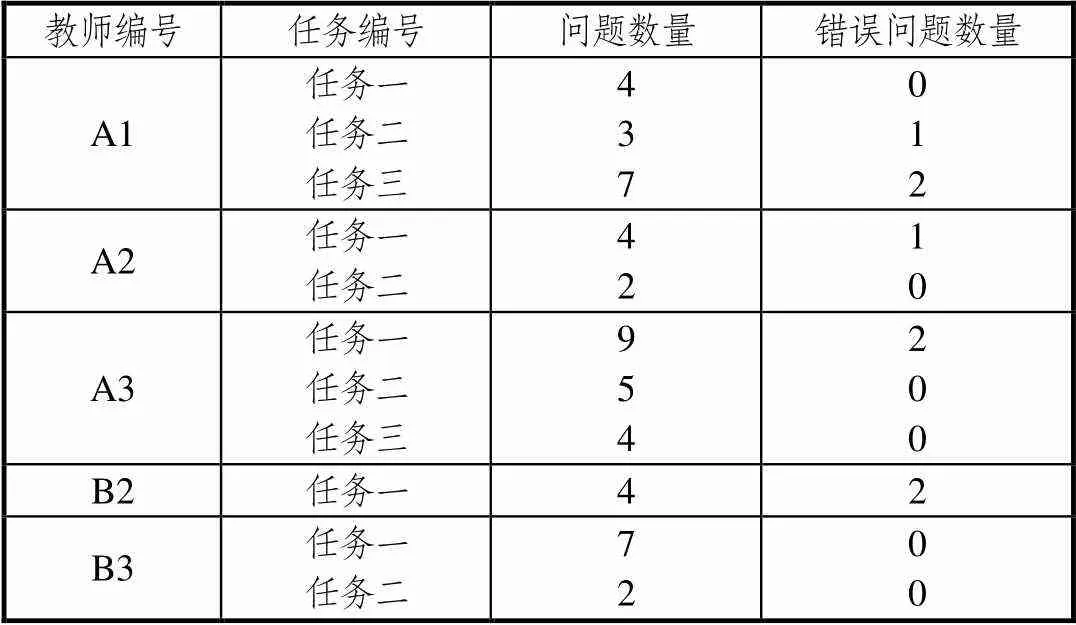
表5 学生提出的数学问题总数及错误问题数
5节课中的问题提出活动都遵循了前述问题提出教学的大致过程,即教师出示问题提出任务后,学生提出问题,再由教师总结学生提出的数学问题或选取一个或多个问题并解决.由于课堂教学时间有限,教师不可能解决学生提出的每一个问题,如何处理学生提出的数学问题,筛选需要重点解决的问题关乎课堂教学的顺利展开和教学目标的达成.研究发现,尽管5位教师在处理学生提出的问题时有所差异,但可以概括为一个普遍的模式:教师选择与教学目标紧密相关或是与教科书相契合的数学问题来重点解决,忽略了那些与该节课教学目标不太相关的问题.具体来说,A1在学生针对任务一提出的4个数学问题中选取了两个,即教科书中原本呈现的两个整十数加减法的问题,另外两个问题是学生已经学过的内容与该节课教学主题无关,教师只进行了点评,没有组织学生解决;引导学生针对任务二和任务三提出的数学问题进行总结概括:求总和用加法,求相差数、剩余用减法,深化加减法意义的理解.A2对两个问题提出任务中,学生提出的两个能够引发未知数范围讨论的问题进一步延伸,突破教学难点.A3在学生根据3个数学表达式提出丰富的问题情境后,总结学生所提问题情境的特点,遗憾的是没有利用学生所提的问题开展算法和算理的探究.B2由于在引导学生提问时所用的引导语限制了学生思维,教师就学生提出的两个正确的数学问题展开问题解决教学.B3对任务一的一个简单的加法问题和比较大小的问题通过与全班学生快速讨论解决,另外5个问题是该节课要重点探究解决的问题——异分母分数加法和减法,然而学生所提的5个问题与教科书呈现的问题类型相同但并不完全一致,教师并未从学生所提的问题中进行选择,而是拘泥于课本呈现的两个问题继续展开教学;任务二是在练习环节设置的,由于课堂教学时间已经接近尾声,教师和学生快速口头解决了学生提出的两个问题并结束了该节课.可以看出,教师处理学生提出的数学问题的模式折射出教师对教学目标的关注以及对教科书的重视程度,A组教师比B组教师在处理学生所提的数学问题方面更为自然与灵活.
4 结论与讨论
基于课堂视频分析的视角,从教师设置的问题提出任务、处理学生提出的数学问题两个方面对6位不同学习阶段的小学数学教师问题提出课堂教学行为进行分析,主要得出以下结论:(1)除一位教师外,参加不同学习阶段的问题提出教学工作坊的5位小学数学教师能够顺利实施问题提出教学;(2)不同学习阶段的小学数学教师选择的问题提出教学内容领域、设置的任务情境、所用的引导语及选取学生提出的问题方面具有较强的相似性;(3)学习时间较长的教师在课堂教学中设置的问题提出任务的数量、情境类型比学习时间较短的教师更为丰富,为学生提供了更多的学习机会,在处理学生提出的问题时更为灵活.
经过小学数学问题提出教学工作坊不同阶段的学习,多数教师可以不同程度地掌握问题提出教学的基本方法.这再次印证了主题式教师专业发展活动在帮助参培教师消解理论到实践转化困难方面的有效性[18],教师经由工作坊培训后愿意采用问题提出上课,且总体效果不错.B1之所以未能成功将问题提出融入数学课堂教学,可能是以下两方面的原因.一是内部因素,该教师职前教育经历并非数学和教育学专业,且在参加培训时入职不到两年,对小学数学教学内容及教育教学方法还未有清晰的理解与把握.此外,问题提出被认为是一种不太常规的教学手段,对于该教师而言,操作更加困难.二是外部因素,该学员仅参加了第三期工作坊的学习,这一期培训是在前期培训的基础上开展的,更偏重于课堂教学实践,加之培训中展示的课例并非都是真正的问题提出教学,造成该教师对问题提出理解出现偏差.培训中虽然构建了学习共同体,但采用了随机分组的形式,并未考虑学员教龄等因素,致使新手教师在学习中未得到深入交流学习的机会.虽然该学员有将问题提出运用于课堂教学的欲望,但种种因素导致始终没有付诸实践.
无论是学习时间较长还是学习时间较短的教师,问题提出课堂教学内容不约而同地选择了“数与代数”领域中的内容,设置的问题提出任务情境均是基于现有教科书内容改编而成,且密切关注教学目标,执行问题提出任务时采用比较直接的引导语,对学生问题的选取同样指向教学目标,但对学生提出的错误问题关注度不够.这可能与教材中占比很小的问题提出绝大多数在数与运算领域呈现,空间观念与度量领域中问题提出很少[27]密切相关.教科书是课程标准的具体化,是教师开展教学活动的主要依据,对现有的课程材料稍作修改既不会过多地干扰教学目标和内容,同时也不会给教师增添较多额外的教学负担.另一方面也侧面说明工作坊中设计问题提出任务的方式对学员设计和实施问题提出教学产生了潜移默化的影响,因为对现有教科书的再设计正是工作坊中帮助教师运用问题提出教学的重要方式之一.教师在引导学生提问时的要求明确且细致,可能由于学生在课堂上很少有机会提出问题,明确的指示可以避免造成小学生理解障碍,多次细致地引导能够避免学生出现天马行空的问题,引领学生逐步靠近教学目标,但从某种程度上同时限制了学生的思维和学习机会.选取学生提出的问题与教科书内容保持高度一致,体现出教科书在教师教学中的重要地位及教师对教学目标的关注.由于课堂教学的即时性以及课时的限制,造成教师对于学生提出的“非典型”错误问题没有给予较多关注.
学习时间较长的教师在课堂教学中设置的问题提出任务的数量、类别及情境的类型比学习时间较短的教师更为丰富,为学生提供了更多的学习机会,在选取学生提出的问题时更为灵活.教师专业发展的一般路径表明:教师通过学习,能够促进自身知识的增长和教学信念的转变,进而改进课堂教学行为[28].调查显示,教师在参加工作坊之前并没有或很少有数学问题提出学习的经历及教学经验,教科书中已有的问题提出活动“提出与给定类型的运算相匹配的问题”占比最低,从而说明教师设置问题提出任务情境、类型的差异主要是受不同阶段的工作坊学习经历的影响.4期工作坊的培训内容各有侧重,第三期工作坊在专家理论引领的基础上,围绕小学数学问题提出教学课例的研讨而展开,课例展示、课堂观摩作为广大学员较喜爱的培训形式,虽然能够快速促进他们问题提出实践知识的获得,但理论是实践的先导,对于仅参加第三期工作坊的教师而言,问题提出理论认知不如4期均参加的教师那么深刻.此外,教师的问题提出教学信念在他们如何开展问题提出教学方面起着关键作用,但是教师教学信念具有较强的稳定性,其改变不是一朝一夕之事.小学数学教师的问题提出教学信念的发展是从他们参加工作坊教师专业发展项目开始的,只有持续性的专业发展才能深化教师的问题提出教学信念,从而使得问题提出课堂教学中设置的任务情境、类型等越发多样,为学生创造的学习机会越多.
研究中检视了6位小学数学教师的问题提出课堂教学行为,弥补了当前问题提出实践研究缺乏的些许不足,为一线教师教学实践、教师专业发展活动的变革提供了参考,但仍然存在一定的局限性.首先,样本量可能限制了研究结论的普遍性;其次,由于问题提出作为不太常规的教学手段需要教师花费大量的时间来备课,因此录课课时有限,以致未能在更为丰富的课堂情境中探索教师的问题提出课堂教学行为.未来要使问题提出教学成为常态仍任重而道远,可运用设计研究方法,研究者和一线教师共同设计问题提出的教学任务,而后进行课堂实施,实施后再改进,以形成成熟的问题提出教学案例.还可进行实验研究,探索问题提出教学对学生数学学习的影响.
[1] 林崇德.对未来基础教育的几点思考[J].课程·教材·教法,2016,36(3):3–10.
[2] 朱邦芬.如何学习知识——从一所高中和一个大学物理系的成功谈起[J].清华大学教育研究,2014,35(2):1–7.
[3] CAI J, HWANG S, JIANG C, et al. Problem-posing research in mathematics education: Some answered and unanswered questions [M]. New York: Springer, 2015: 3–34.
[4] EINSTEIN A, INFELD L. The evolution of physics [M]. New York: Simon and Schuster, 1938: 95–96.
[5] 顾明远.不会提问的学生不是学习好的学生[J].福建教育,1998(10):1.
[6] 钟启泉.深度学习:课堂转型的标识[J].全球教育展望,2021,50(1):14–33.
[7] 张辉蓉,冉彦桃,刘蝶,等.教师“问题提出”教学知识建构[J].数学教育学报,2019,28(2):13–17.
[8] 张玲,宋乃庆,蔡金法.问题提出:基本蕴涵与教育价值[J].中国电化教育,2019(12):31–39.
[9] NCTM. Curriculum and evaluation standards for school mathematics [M]. Reston: NCTM, 1989: 22–28.
[10] 陈婷,李兰,蔡金法.中国小学数学“问题提出”教学的研究与实践——基于《小学数学教师》和《小学教学》(数学版)中“问题提出”文章的分析[J].数学教育学报,2021,30(1):19–24.
[11] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:8.
[12] 日本文部科学省.中学校学习指导要领解说·数学编[M].东京:东洋馆出版社,2008:31.
[13] CAI J, JIANG C. An analysis of problem-posing tasks in Chinese and US elementary mathematics textbooks [J]. International Journal of Science and Mathematics Education, 2017, 15 (8): 1 521–1 540.
[14] 胡典顺,薛亚乔,王明巧.中国和美国小学数学教材中问题提出的比较研究[J].数学教育学报,2016,25(4):37–41.
[15] CAI J, HWANG S. Teachers as redesigners of curriculum to teach mathematics through problem posing: Conceptualiza- tion and initial findings of a problem-posing project [J]. ZDM Mathematics Education, 2021 (53): 1 403–1 416.
[16] 李欣莲,宋乃庆,陈婷,等.小学数学教师“问题提出”表现研究[J].数学教育学报,2019,28(2):1–6.
[17] 宋乃庆,周莞婷,陈婷,等.小学数学教师“问题提出”的教学信念研究[J].数学教育学报,2019,28(4):24–29.
[18] 宋乃庆,张莎莎,陈婷,等.基于“问题提出”的小学数学教师主题式专业发展:理论建构与实践探索[J].数学教育学报,2021,30(1):12–18.
[19] ZHANG H, CAI J. Teaching mathematics through problem posing: Insights from an analysis of teaching cases [J]. ZDM Mathematics Education, 2021 (53): 961–973.
[20] LI X, SONG N, HWANG S, et al. Learning to teach mathematics through problem posing: Teachers’ beliefs and performance on problem posing [J]. Educational Studies in Mathematics, 2020, 105 (3): 1–23.
[21] 蔡金法.中美学生数学学习的系列实证研究:他山之石,何以攻玉[M].北京:教育科学出版社,2007:277.
[22] 蔡金法.小学数学教师的专业素养——以如何上好一堂课的视角来探讨[J].小学教学(数学版),2014(Z1):10–14.
[23] 喻平.教学认识信念研究[M].北京:科学出版社,2016:167.
[24] 许天来,蔡金法.作为教学目标和教学手段的数学问题提出[J].小学教学(数学版),2019(10):9–14.
[25] 徐冉冉,李丹杨,姚一玲,等.指向教学改进的“问题提出”数学教学[J].数学教学,2020(10):1–8.
[26] CAI J, SILBER S. Pre-service teachers’ free and structured mathematical problem posing [J]. International Journal of Mathematical Education in Science & Technology, 2017, 48 (1–2): 163–184.
[27] 胡典顺,蔡金法,聂必凯.数学问题提出与课程演变:两个版本小学数学教材的比较[J].课程·教材·教法,2015,35(7):75–79,36.
[28] CAI J. Longitudinally investigating the effect of teacher professional development on instructional practice and student learning: A focus on mathematical problem posing [Z]. Newark, DE: The University of Delaware Unpublished Manuscript, 2017.
Research on “Problem Posing” Classroom Teaching Behaviors of Elementary Mathematics Teachers
ZHANG Sha-sha1, SONG Nai-qing1, 2, CAI Jin-fa3
(1. School of Mathematics and Statistics, Southwest University, Chongqing 400715, China;2. Faculty of Education, Southwest University, Chongqing 400715, China;3. Department of Mathematics, University of Delaware, Newark DE 19716, USA)
Based on the analysis of classroom teaching video, taking 6 teachers who participated in the “problem posing” teaching workshop in elementary mathematics in Chongqing as the object, this paper analyzes the “problem posing” classroom teaching behaviors of elementary mathematics teachers from two aspects: the setting of problem posing teaching tasks and dealing with the mathematical problems posed by students. The study found that except one teacher, five elementary mathematics teachers can basically successfully implement the problem posing teaching after participating in the workshop. There are strong similarities in the field of teaching content they choose, the prompts used in performing tasks and screening the problems posed by students; Teachers with long learning time set more problem posing teaching tasks, situation types in classroom teaching and they provide more learning opportunities for students and are more flexible in dealing with students' problems than teachers with short learning time. These findings further illustrate the effectiveness of the workshop in helping elementary mathematics teachers with teaching through problem posing.
elementary mathematics teachers; problem posing; classroom teaching behaviors
2021–10–26
国家社科基金后期资助项目——中小学问题提出的理论与实践探索(20FJKB006);西南大学引进人才(教育部“长江学者”讲座教授)计划项目——数学问题提出对教师专业发展和学生创新能力提升的长期跟踪研究(SWU118118);小学数学教师“问题提出”教学能力测评模型构建研究(2021-06-020-BZPK01);北京师范大学中国基础教育质量监测协同创新中心研究生自主课题资助(BJZK-2018A1-18012)
张莎莎(1990—),女,河南安阳人,博士生,主要从事数学教育研究.
G623
A
1004–9894(2022)02–0046–07
张莎莎,宋乃庆,蔡金法.小学数学教师“问题提出”课堂教学行为研究[J].数学教育学报,2022,31(2):46-52.
[责任编校:周学智、陈汉君]
