认知弹性理论下的结构不良试题探析——以“2021年全国甲卷理科数学第18题”为例

高田田 陈豫眉

(西华师范大学数学与信息学院,637002)

认知弹性理论最早是斯皮罗提出的,他依据知识的复杂程度,将知识分为结构良好领域的知识和结构不良领域的知识,强调知识的情境性．从学习观的维度来看,他提出将学习分为初级学习和高级学习,高级学习阶段强调掌握概念的复杂性,要求学生能够有效利用已习得的知识分析新的情境,同时能够将己有的知识迁移至新的情境中去,灵活解决问题[1]．

所谓结构不良试题,是相对于结构良好试题而言的,并不是指试题本身有误,而是指构成问题的初始状态、算子、目标状态三者存在某种不确定性,因而通常没有所谓的标准答案．解决结构不良问题，能有效地激发学生学习的求知欲,帮助学生从多个方面去把握问题的本质,追求知识蕴含的价值,有效形成跨学科综合解决问题的能力．因此,结构不良试题对促进学生的素养养成和学习能力的提升具有重要意义[2]．

基于认知弹性理论,斯皮罗提出解决结构不良问题的两大原则,一是“多元表征”,从多个角度审视问题,增强学生知识迁移的能力;二是建立“纵横交叉形”知识结构,从多个维度展示知识与知识之间、知识与情境之间的联系,提高学生应用知识的能力.在此基础上，本文依据问题解决的一般过程,把结构不良问题解决的过程划分为三阶段:表征问题空间阶段、解决问题阶段、评估解决方案阶段．下面以一道高考题为例，对此进行探究.

试题呈现(2021年全国甲卷理科数学18题)已知数列{an}的各项均为正数,记Sn为{an}的前n项和,从下面① ② ③ 中选取两个作为条件,证明另外一个成立．

① 数列{an}是等差数列;

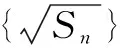
③a2=3a1．

注若选择不同的组合分别解答,则按第一个解答计分．

一、表征问题空间

该题给出三个条件,要求在三个条件中选取两个作为题目的条件,剩下一个作为要证明的结论,共有三种组合方式:选择① ② 为条件，选择① ③ 为条件或选择② ③ 为条件．该题作为结构不良试题,由三道结构良好试题组成,每个结构良好的试题都要进行一次表征．

该题考察的是数列问题,主要是进行抽象表征,显性条件是已知数列{an}的各项均为正数,Sn为{an}的前n项和;隐性条件是首项a1是正数,若数列{an}是等差数列,则公差d>0；若数列{an}是等比数列,则公比q>0．若之后遇到解析几何、立体几何等试题,可结合文字、数式、图表等进行形象表征．

面对三种组合方式,学生脑中会浮现几个问题：(1)每个条件都有意义吗?是否与初始条件矛盾?(2)这三种组合方式都可以证明出最后结论吗?(3)哪种组合方式解题更简单?(4)需要运用哪些知识?(5)是否有多种解题途径?(6)哪种解题途径更快捷?

二、解决问题的过程

从三个待用条件中选取两个作为条件,剩下的一个为要证明的结论,共有三种选法．

情形1选择① ③ 为条件．

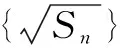
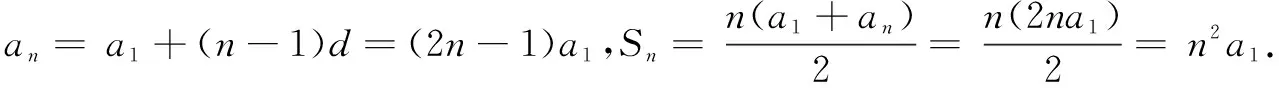
情形2选择① ② 为条件．

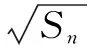
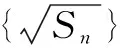
情形3选择② ③ 为条件(也是全国卷甲卷文科第18题)

分析要证明{an}为等差数列,转化为证明an-an-1是一个常数,利用an=Sn-Sn-1求出an的通项公式,注意一定要讨论n=1的特殊情况．

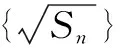
注在实施解决方案过程中可能会遇到许多事先无法预料的突发情况,因此,必须对其进行弹性监控,不断调整和评价解决方案的实际效果．随着问题状态的变化,解决方案需要不断地修改与完善．

三、评估解决方案

本题以数列为背景,考察等差数列的定义,an与Sn之间的转化,等差中项的性质及等差数列基本量的计算等,显然情形1的解题思路学生接触较多,较为容易想到．

而2020年新高考Ⅰ卷第17题,从探究三角形存在有意义的角度而言,选择条件③ 会与初始条件矛盾,可见条件③ 的推理具有不可行性．而本题每个条件的推理都具有可行性,无形中降低了难度．此类问题需要考生依靠问题界定的初始条件,通过分析每一个条件选项的可行性,根据既往经验和现有情境对条件选项一一作出预测性判断,然后选择一个最佳的、最合情的条件进行尝试性探究[3]．

本题是在限定的三个条件中选两个作为条件,另一个作为结论,原题就变成一个结构良好的封闭题．这种题型有一定的开放性,但开放度非常有限．所以我们把这种题称为半结构不良题更为合适[4].但即使是以这样的半结构不良题作为试题,也是高考历史上的一大突破．虽然此题难度不大,但要求学生通盘考虑所给的三个条件,对给出的三个条件进行预判,选出最利于解决问题的条件．这种要求学生先分析后选择的试题,考查学生对数学本质的理解和对数学问题的洞察力,从而真正考查了学生的数学核心素养．作为全国卷甲卷,又是新开发的题型,因此命题者在问题的设置上降低了很多难度.一方面在问题设置上并没有要求考生自行补充条件,并且缺少的条件不多,命题者给出3个条件让考生来选择;另一方面,题目放在解答题18题的位置,通过数列这类高考要求不高的题目来设置问题，也降低了难度要求．今后是否可能会在要求更高的立体几何、解析几何或导数中引入此类题型还不清楚[5]．

四、建议

学生所遇到的题目基本都是结构良好的题目,通常采用题海战术,找寻问题的规律,增强对概念的掌握,形成解题的一般模式．但在日常生活中所遇到的问题大多属于结构不良问题,基于弹性认知理论,笔者提出以下几点建议．(1)学生面对结构不良试题时要注重对试题进行多元表征,多维分析,发展自身的弹性认识;(2)在运用案例进行实际学习时,不应将案例与相应的知识点进行简单的“一一配对”,而是应当实现不同情境与知识之间的相互联系,面对一个知识点,要使用多个相关的、代表不同情境的案例来帮助理解,最终形成一个知识点和相应的案例所交替构成的“纵横交叉形”结构;(3)教师要为学生创造尽可能贴近真实数学问题的学习情境;(4)教师可以利用现代信息技术，以具有概括性强的数学概念为主干,以相关的案例为分支,将数学概念镶嵌在多个与其相关的背景案例中,利用真实情境实现数学概念之间的联系,形成概念群．学生可以依据自身情况,选择一个案例情境进入,展开自主学习,构建具有个人特色且能够灵活迁移的数学知识结构．