问题驱动探究 落实核心素养*——以“空间向量基本定理”教学设计为例

宋 军 吴现荣

(贵州省都匀第一中学，558000) (黔南民族师范学院数学与统计学院，558000)

《普通高中数学课程标准》(2017年版)指出,定理教学的意义不仅在于让学生掌握“书本知识”,更重要的是让他们从中体验数学家概括数学定理的心路历程．美国数学家哈尔斯说过，“问题是数学的心脏”,问题是思维活动进行的原动力和牵引力,而数学核心素养又是在学生与情境、问题的有效互动中得到提升的．为了体验数学家发现空间向量基本定理的心路历程,追寻数学发展的历史足迹,把数学的学术形态转化为学生易于接受的教育形态,根据空间向量基本定理产生的背景和它发展的需要等方面去设计“前后一致逻辑连贯”、符合学生思维发展水平的问题.在这些问题的驱动下,不仅能使学生在发现、探究、思考中完成定理的自然习得,还能发展和落实数学抽象、直观想象、逻辑推理等数学核心素养,培养终身学习的兴趣．本文以“空间向量基本定理”教学设计为例，对此进行探讨.

一、设置问题,引入课题

问题1(1)两个向量有什么关系?是怎样研究的?

生:共线与不共线,由向量共线的条件知研究共线问题,也就同时研究了不共线问题．

(2)三个向量有什么关系?怎样研究?

生:共面与不共面,由平面向量基本定理，研究共面问题,也就同时研究了不共面问题．

(3)四个向量有什么关系?怎样研究?

师:在(1)(2)的基础上,类比是重要的:两个向量共线,一个向量用另一个向量表示;三个向量共面,一个向量用另外两个(此时这两个向量不共线)向量表示,叫做平面向量基本定理;四个向量呢?一个向量能否用另外三个(此时这三个向量不共面)向量表示吗?怎样表示?

设计意图数学知识的内部发展促进知识的自然延伸或突破,这种从数学内部提出问题,有利于发挥数学发展的内部动力,有利于建立“前后一致,逻辑连贯”的数学学习过程．

①

设计意图用向量的减法知识解决问题2,该问题的结论是空间向量基本定理的特例,其特殊在于点P在平面ABC上．

②

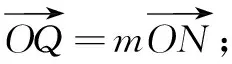
③

问题4由① ② ③ 有何发现?

设计意图让学生直观感知空间向量基本定理,从具体的素材“平面向量基本定理”模型中经历一个从直观的“形”到具体的“数”的抽象概括过程,使空间向量基本定理的生成自然而然,发展学生的数学抽象素养．

问题5请同学们分别作出下列向量,这些向量都在上述直线OA,OB,OC构成的空间内吗?

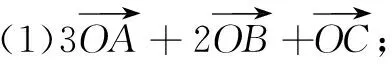
设计意图让学生自己动手作图验证、操作确认,自然水到渠成地得到定理,深刻理解定理的形成过程．

二、 抽象概括,诠释定理

师:若将所有的向量的始点放在一起,则整个空间被向量的终点填满．即空间内的任意向量都可以用三个不共面向量的表示;反之,由这三个不共面向量表示的向量都在这个空间内．于是有:

空间向量基本定理如果e1,e2,e3是空间内的三个不共面向量,那么对于这一空间内的任意向量p,存在唯一的实数组λ1,λ2,λ3,使得p=λ1e1+λ2e2+λ3e3．

我们把不共面的向量e1,e2,e3叫做表示这一空间内所有向量的一组基底．定理中给定一组基底,表示向量p的实数λ1,λ2,λ3的唯一性可从代数角度作如下证明:

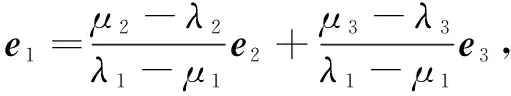
问题6在空间向量基本定理中的实数λ1,λ2,λ3的任意性和唯一性,当λ3=0中它是什么定理?当λ2=λ3=0时它是什么定理?

设计意图理解有关定理间的联系,事实上,一个非零向量可以表示与之共线的任一向量,两个不共线的向量可以表示与之共面的任一向量,这正是由一维的向量共线条件推广到二维的平面向量基本定理,再进一步推广到三维的空间向量基本定理,这种表示是唯一的．这三个结论都可看成向量分解的唯一性,只不过范围不同而已,体现了类比思想,从而形成数学定理体系,有利于定理的内化、迁移与灵活应用．

三、例题讲解,加深理解

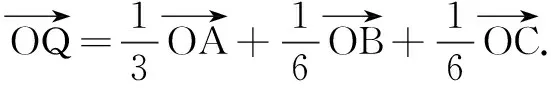
设计意图解此类问题的关键是找所求向量与基底间的关系,运用向量加减法的平行四边形法则和三角形法则来寻求．这一过程体现转化与化归的思想,体会基底选择的重要性,选定空间不共面的三个向量作基底后,任意空间向量,都用基底来表示,为向量的运算提供极大的便利,同时也是用空间向量解决立体几何的基本出发点．

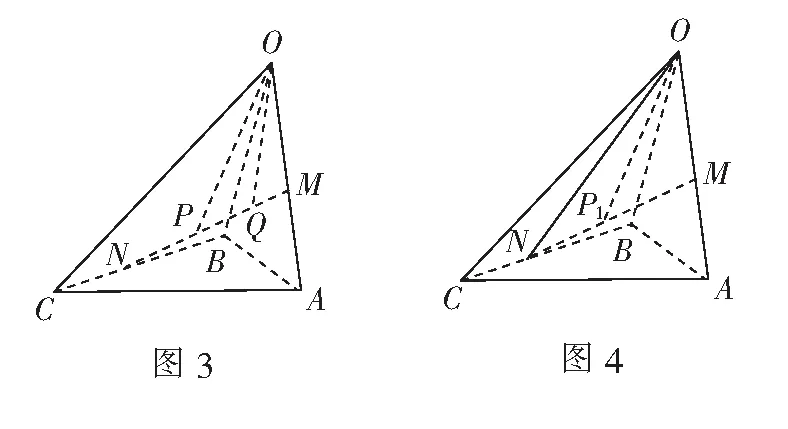
变式求证四面体对棱中点的连线交于一点,且互相平分．

设计意图空间向量基本定理解决几何问题的通解通法是选好一组不共面的基底,并用它们表征其余空间向量,体现了向量基底的思想,进一步深化对空间向量基本定理的认识,感受到向量数形二重性在证明空间几何问题中的独特魅力．

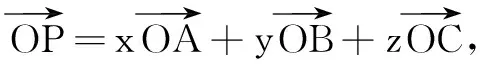
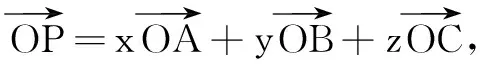
设计意图从一般到特殊,回归教材选修2-1第88页思考题的第2个问题,这更有利于理解空间向量基本定理．

四、课堂小结,反思提炼

(1)提出问题的方法:从向量线性运算的问题引出“用不共线的两个向量表示平面内任意向量”的研究课题,这样做到承前启后,达到“自然且水到渠成”引入学习内容的效果．

(2)研究的基本思路:从特殊到一般,获得一般规律的猜想,再进行严格的逻辑论证．

(3)归纳概括定理的内涵,通过例题说明基底的作用．

(4)提出正交分解和坐标表示的研究任务:将基底特殊化“e1⊥e2,e1⊥e3,e2⊥e3,|e1|=|e2|=|e3|=1”．并将定理与空间直角坐标系联系起来,有什么新发现?