落实“三会” 提升素养
2022-04-11孔新华
孔新华
(江苏省木渎高级中学,215101)
我国发展学生素养的核心体系是从培养学生应具备的正确价值观,以适应终身发展和社会发展的需要,重视处理人与自我、人与世界的关系.“社会参与”、“自主发展”维度的许多指标都表明了这一点.例如“能够用科学的思维来理解事物、解决问题和指导行为”,“自觉而有效地获取、评估、识别和使用信息”,“具有数字化生存能力并积极使用‘互联网+’等社会信息化发展趋势”,“善于发现和提出问题,对解决问题有兴趣和热情,并能够根据特定情况和特定条件选择和确定合理的解决方案”.落实到数学学科,便细化为会用数学眼光观察世界, 会用数学思维思考世界, 会用数学语言表达世界,即通常简称的“三会”.“三会”生动地描绘了数学育人功能中的三个重要特征:“数学眼光,数学思维和数学语言”.这三个在数学学习中的行为往往是相互关联的,是数学核心素养被“内化”的结果.从数学的角度看世界,需要学生具有“数学抽象”和“直观想象力”的能力;使用数学思维思考世界,需要学生具备“逻辑推理”和“数学运算”的能力;用数学语言表达世界,需要学生具备“数学建模”和“数据分析”的能力.
本文结合课堂教学中的实例,谈谈如何在课堂教学中落实学生的“三会”,从而达到数学核心素养的提升.
一、会用数学眼光观察世界
生活中无处不数学,观察各种现象要多从数学的角度出发,形成数学眼光,培养深度思考能力,看到他人所看不到的.数学眼光就是从数学现象中抽象出数学本质.在教学中,要利用切合学生实际的情境,引导学生用数学的眼光观察问题、发现问题,使用恰当的数学语言、模型描述问题,用数学的思想、方法解决问题,从而提高学生的数学学科核心素养.
案例1(饮料罐问题)某饮料厂为降低成本 ,要将某罐装材料降到最小,假设此罐装饮料筒为正圆柱体(视上、下底面为平面),上、下底面圆的半径为R,高为h,若体积为V,试问当R与h之比是多少时用料最少?
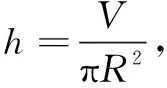
设计意图用基本不等式或导数可以得到结果.在建模活动设计时,如果直接给出数据,就容易变成应用题了.加了“头”、“尾”活动,给学生一定的自主发散的空间,也有利于教师在过程中的观察和评价.
还可以将问题延伸:请学生到市场上作调查,研究哪些饮料的罐体大体上符合或者不符合自己的计算结果,并尝试解释其原因.考虑到饮料罐的手持性,便于冷藏或加热,饮料罐的上下底厚度和侧面的厚度有差异,导致用料的变化,同时还要考虑运输和销售成本,这样会产生误差,才会出现现实中我们看见的各种形状.
数学建模是一种“问题引领”、向学生生活领域延伸的数学化方式与途径.要求学生能够从问题情境中提出、发现、理解、解决问题并能够适当拓展问题.强调数学与生活、数学与学生已有的学习经验的联系.从而学生用数学眼光观察世界的能力便得到很大提升.
二、会用数学思维思考世界
用数学思维思考世界主要途径就是在整个数学学习的过程渗透逻辑推理.在数学探究活动中充分发挥不同推理形式的功能,从而提高学生的数学思维品质.思维是人的心理活动的一种高级形式.思维指的是人脑对客观现实的概括和间接反映,属于人脑的基本活动形式.数学思维就是用数学思考问题和解决问题的思维活动形式.逻辑推理是数学学科的重要特点,贯穿于整个数学学习和应用的过程.在探索解决问题的过程中,思路的形成随着问题的难易程度和表述形式都体现水平的差异.




数学课堂教学肩负着传承科学精神和理性文明的历史使命,应着力于揭示数学本质,培养学生的数学思维,从而让学生的数学思维得到发展,在生动活泼的数学思维活动中提升数学核心素养.这样通过典型的例子的自主探索,体验数学思维在实际问题中探索的过程与方法,并享受到成功的喜悦,是学生喜闻乐见的教育形态.
三、会用数学语言表达世界
数学学习离不开数学语言表达能力,如何将语言应用能力通过数学思维,数学语言表达等途径将之内化?这就要求在课堂教学中十分重视数学的语言表达,才能使数学语言应用能力得到提升,从而真正使数学核心素养得到提升.数学建模是对实际问题数学化,即用数学的语言去表达问题、用数学的方法构建模型,通过数学模型的解决去解决实际问题.数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、确定参数、计算求解、检验结果、改进模型,最终解决实际问题[1].
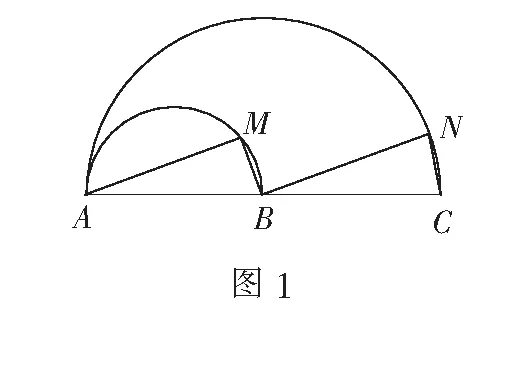
案例3太阳冉冉升起,波光粼粼的海面格外美丽,然而危险常常与美丽同在,冰山、暗礁不断考验着航行的船只.一艘轮船在沿东北方向直线航行的途中,某时刻观测到位于轮船正东40海里处有一座小岛.距离该岛30海里以内的圆形海域布满了暗礁.如果这艘轮船不改变航线,继续航行,那么它是否有触礁的危险?轮船沿什么方向航行恰好与暗礁区“擦肩而过”?
解析该问题的本质是直线与圆的位置关系.以小岛为原点O,东西方向为x轴,建立如图2所示直角坐标系,则圆O的方程为x2+y2=900,轮船所在位置P(-40,0).
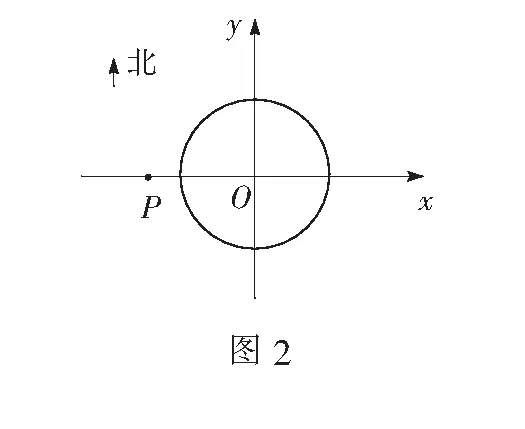
(1)航线所在直线方程为x-y+40=0.
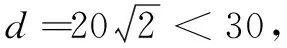

(2)若航线所在直线垂直于x轴,则与圆相离,不符合题意.
故可设航线所在直线l的方程为y=k(x+40).
方法1O到l的距离d=30,解得
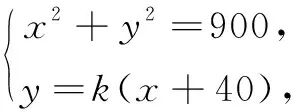
(3)此航线处在暗礁区的长度是多少?

方法2① 由x2+40x+350=0, 求得两交点坐标,用两点间距离公式;
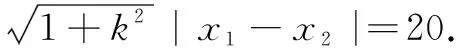
用数学语言表达世界,即能够把情境数学化,从情境中抽象出数学概念并用数学的语言提出问题的.具体表现在日常生活和实践中善于运用数学思想方法去思考和解决问题,会用一般性思维去思考问题,能透过现象把握本质、以简驭繁.数学教育要在人与世界之间搭建起一座座数学的“立交桥”.这是在发展学生核心素养的主旨之下,数学课程在处理人与自我、人与社会、人与环境关系上的自觉的价值拓展,展现了勇于克服种种教育功利羁绊的育人大视野.
教育就是为了育人,立德树人,把教育的宗旨定在人的发展上,这就超越了知识,更超越了分数,甚至超越了能力.让人成为目的,让学生站在教育的中央,让教师与学生都成为学习者,这些都是全球教育共同面临并正在探索的问题[2].
