针对特高压直流接入受端电网的TCSC装置定容选址规划

李湘旗，章 德，廖长风，李 勇，马俊杰

(1.国网湖南省电力有限公司经济技术研究院，湖南 长沙 410007；2.湖南大学电气与信息工程学院，湖南 长沙 410082)

中国的新能源与负荷的分布在地域上存在着严重不匹配的情况，为满足西电东送的需求，中国正在大力发展大容量、远距离特高压直流输电技术[1]。受益于高输送容量和较低的建造成本，基于电网换相换流器(line-commutated converter, LCC)的高压直流输电(high voltage direct current, HVDC)技术目前在中国应用最为广泛[2]。然而，LCC-HVDC存在换相失败的问题，在发生连续换相失败情况下，将会导致直流保护动作出口闭锁[3]，给受端电网造成严重不利影响。目前，中国绝大多数大规模交直流混联系统都呈现着“强直弱交”特征，交流系统网架结构较为薄弱。以2025年湖南电网目标网架为例，在规划方案中，有一回±800 kV特高压直流落点湘南地区。当系统发生直流闭锁故障后，将通过与外部电网联络通道紧急调度来填补有功缺额，而大规模的潮流转移可能会导致部分线路过载，造成系统输电阻塞问题，从而大面积切负荷，给系统带来严重经济损失。

针对输电阻塞问题，已有许多研究者提出了相应改善方案。文献[4-5]分别针对自由电力市场下和大规模风电接入下系统潮流变化造成的线路过载问题，提出了传输线路切换优化模型，通过切除部分传输线路来满足线路潮流安全约束。这种方式虽然可以在一定程度上改善潮流分布，但无法最大化利用系统线路传输容量，当系统发生大规模潮流转移时，仍可能导致部分线路过载，给电力系统稳定运行带来严重影响。新建变电站及输电线路虽可以有效地解决输电阻塞问题，然而新建变电站存在经济性差且选址困难的问题[6]。文献[7-8]基于晶闸管控制的串联电容器(thyristor controlled series capacitor, TCSC)提出了一种电力系统阻塞疏导方法，TCSC可以通过连续地调节所补偿线路的电抗来控制线路潮流[9]，进而可以高效地缓解系统输电阻塞问题；文献[10]基于TCSC改善了风电并网对网络功率分布的影响。除此之外，还可以通过TCSC的快速响应能力提升系统的暂态稳定性[11]以及降低系统的短路电流水平[12]。因此，为满足含特高压接入受端系统发生直流闭锁故障后的大规模潮流转移需求，亟需要一种针对该系统的TCSC装置定容选址规划方法。

本文将LCC-HVDC直流闭锁故障作为安全约束加入到规划模型中。目前针对安全约束下规划问题，已有大量文献做了相关研究。文献[13]采用模糊聚类法将风电场和负荷出力的数据聚类成多个确定性的运行场景，提出了计及N-1安全约束的含风电场输电网扩展规划模型；文献[14]基于安全距离模型，配电网N-1安全评估方法和指标，提出一种考虑N-1安全的多目标DG选址定容规划模型；文献[15]为了在改变系统网架结构的同时保证系统安全性，建立考虑N-1安全网络约束的输电网结构优化模型；文献[16]分析了考虑节点电压限制和N-1潮流约束的DG出力上限求解方法，提出了一种考虑N-1安全约束的DG出力控制可视化方法；文献[17]建立了考虑风电和负荷波动及系统N-1故障多场景的备用容量优化模型。文献[13-17]中提出的N-1规划方案，虽能有效地保证系统安全性，但也导致了N-1安全约束下最优潮流问题规模大，计算耗时长的问题[18]。文献[19]提出了将机组组合与电网线路N-1安全校核直接闭环的发电计划优化模型。然而其N-1故障校核中，没有设置切负荷等紧急控制方案。文献[20]提出在含可再生能源接入的电力系统输电网络结构优化模型，将该优化问题分为经济调度问题和N-1校验问题，2个问题交替求解。对输电网结构和机组出力进行优化，文献[21]利用多场景技术对风电、负荷的不确定性进行建模，在此基础上建立了计及N-1安全网络约束的发输电双层随机规划模型。文献[19-21]中下层N-1校验均选取造成系统切负荷的N-1故障返回上层，然而造成系统切负荷的故障不均是对系统整体造成影响最大的故障，且当针对特高压直流接入的受端系统发生直流闭锁故障时，可能无法避免采取切负荷紧急控制。故本文选取新的指标判断下层N-1故障是否通过校验，返回上层规划。

针对上述文献分析，本文建立了针对特高压直流接入受端电网的TCSC装置定容选址规划模型。所提模型主要创新点包括：

1)针对特高压直流接入受端系统发生直流闭锁故障后所造成大规模潮流转移问题，通过加装TCSC装置进行改善；

2)综合考虑TCSC投资建设成本及系统运行成本，构建双层规划模型，降低了N-1约束下优化规划的求解难度；

3)下层N-1故障校验中，通过各机组有功出力与最优出力的偏移量选取对系统造成严重影响的故障返回上层，进行规划优化。

1 规划模型

1.1 TCSC工作原理

TCSC工作原理如图1所示，Xij为原线路电抗；XTCSC为晶闸管控制串联电容器，为可运行在容性状态或感性状态。运行在容性状态下时，线路电抗减小，有功潮流增加；运行在感性状态下时，线路电抗增加，有功潮流减小。

图1 TCSC等效电路模型Figure 1 Equivalent circuit of TCSC

通过加装TCSC，节点i与节点j之间线路电抗将被调节为

XL=Xij+XTCSC

(1)

将TCSC的控制作用等效为系统线路传输功率，不需要对系统原导纳矩阵做任何修改[22]。支路有功潮流可计算为

(2)

1.2 上层规划模型

1)目标函数。考虑TCSC装置建设的经济性，TCSC定容选址规划模型中，上层模型以加装TCSC装置投资成本最小为目标，上层目标函数设定为

(3)

2)等式约束。节点潮流方程为

(4)

支路潮流方程为

(5)

式中lij,s为线路状态。若线路正常运行，则值为1，若线路因故障而断开，则值为0。

3)不等式约束。支路潮流约束为

Pij,min≤Pij,s≤Pij,max

(6)

式中Pij,min、Pij,max分别为支路传输功率上、下限。

发电机出力及调节约束为

(7)

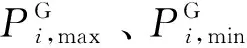
联络通道功率传输约束为

(8)

切负荷约束为

(9)

TCSC调节约束为

(10)

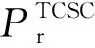
最低运行成本约束为

(11)

1.3 下层优化模型

下层优化模型以运行成本最小为目标，考虑了节点潮流方程等等式约束和发电机出力及调节等不等式约束。在上层规划给出TCSC配置方案基础上进行最优潮流计算。通过计算结果分析给出对系统造成影响较大的N-1故障及其最低运行成本，各发电机及联络通道有功出力区间，并返回上层。

(12)

2 模型求解

为改善由于加入多个N-1安全约束所造成的优化模型规模增加的问题，并同时考虑TCSC装置加装成本及系统运行成本，本文将规划模型分为上层TCSC定容选址规划和下层最优潮流。通过下层最优潮流优化结果分析选取对系统造成严重影响的N-1故障作为约束返回上层，上层针对这些故障进行TCSC定容选址规划，并将规划结果再次传递给下层，通过上下层相互迭代得到最终规划结果。

其中，下层最优潮流主要包含以下3个部分。

2)考虑各单独N-1安全约束下最优潮流模型。判断各故障下发电机及联络通道在最优潮流下，有功出力是否在有功出力区间内，如若不在，则说明系统需要对此N-1故障进行较强的预防控制，将对系统造成影响较大的N-1故障返回上层。

3)考虑全部N-1安全约束下最优潮流模型。本文在上层规划中还加入了最低运行成本约束，通过求解含全部N-1故障下的最优潮流得出每个故障下的最低运行成本。

具体求解过程如图2所示。

图2 算法流程Figure 2 Algorithm flowchart

3 算例分析

3.1 仿真算例

在修改后的IEEE 39节点中，对本文提出优化模型进行验证。系统拓扑结构如图3所示，原IEEE 39节点系统中，31节点与39节点上发电机替换为外部大电网联络通道，17节点上接入一条特高压直流输电线路，输送有功功率为1 000 MW，各故障设置如表1所示。可中断负荷节点设置为3、4、7、8、18，可中断负荷量设置为节点负荷总量50%。故障后运行状态下，发电机有功可调节量设置为系统最大有功出力的10%，pf均设置为0.05。系统中各成本参数如表2所示。系统连接发电机，联络通道及特高压直流线路潮流约束设置为600 MV·A，其余线路潮流约束Pij,max如表3所示，系统基准容量设置为100 MV·A。每条线路上安装TCSC装置单位上限为5组，每组额定容量为20 MV·A[12]。本文所提出的上下层规划优化模型在GAMS中采用SBB求解器进行求解，算法流程通过MATLAB实现。

图3 算例拓扑Figure 3 Topology of test system

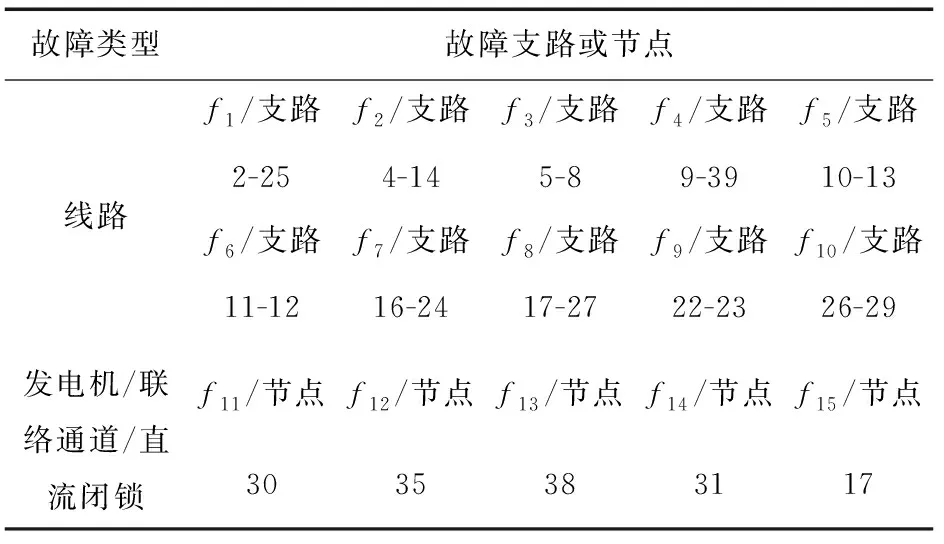
表1 故障设置Table 1 Fault settings

表2 系统成本系数Table 2 System cost coefficient $/MW·h

表3 线路潮流约束参数Table 3 Branch power flow constraints parameter

3.2 算例结果分析

图4 安装不同数目TCSC装置下的最优解Figure 4 Optimal solution with different TCSC numbers

此外，对加装TCSC装置前后系统，在直流闭锁故障后，对各元器件状态进行分析比较，研究TCSC装置在系统发生直流闭锁故障后所起到的具体作用。选取支路传输功率上限Pij,max=5，系统发生直流闭锁故障后最优潮流分布如图5所示，各元器件状态如表4、5所示。当系统发生直流闭锁故障后，主要通过联络通道紧急调度来填补系统出现的大量有功缺额，进而系统无法避免的出现大规模潮流转移。然而线路3(2-3)已经达到支路潮流约束上线，无法继续增加有功传输量，从而导致节点3切除负荷0.709 p.u.，当系统加装TCSC装置后，可通过线路40(25-26)上TCSC装置增加向节点26上功率传输，进而通过线路42(26-27)、31(17-27)、30(17-18)、7(3-18)增加对节点3的有功功率传输。从而有效地改善了系统由于大规模潮流转移所导致输电阻塞而造成的切负荷。因此，本文提出TCSC装置规划模型能够有效地改善含特高压直流接入受端系统直流闭锁故障下的切负荷问题。

图5 直流闭锁故障后系统最优潮流(Pij,max=5)Figure 5 Optimal power flow after DC blocking fault

表4 直流闭锁故障后发电机出力结果对比Table 4 Generator output after DC blocking fault

表5 直流闭锁故障后切负荷结果对比Table 5 Load shedding after DC blocking fault

4 结语

本文提出了一种针对含特高压直流接入的受端系统TCSC装置定容选址双层规划模型，同时考虑了TCSC装置加装成本与系统运行成本。下层规划选取对系统最优潮流造成影响较大的故障返回上层，通过迭代得到数组有效优化解。

通过不同支路潮流约束下的优化结果对比可知，受端交流系统网架越薄弱，故障下潮流转移时输电阻塞问题越为严重，TCSC对此问题的改善效果越加显著。因此，针对中国特高压直流接入下受端系统网架大多存在“强直弱交”问题，本文所提方法模型能够取得良好改善效果。直流闭锁故障后各元器件的状态对比结果表明，通过TCSC装置控制潮流可以有效地解决系统发生直流闭锁故障后发生大规模潮流转移导致的线路过载所造成切负荷问题。综上，本文所提出TCSC装置定容选址双层规划模型可同时提高含特高压接入受端系统的经济性和稳定性。