角度对梁柱四角钢连接节点力学性能的影响
2022-04-11龚富涛孙国华
龚富涛,孙国华
(苏州科技大学 土木工程学院,江苏 苏州 215011)
当前建筑设计越来越追求新颖和美观,各种复杂结构日益增多,抗弯钢框架中梁柱斜交情况越来越多。我国《高层民用建筑钢结构技术规程》(JGJ 99-2015)[1]仅对钢框架结构的梁柱正交连接节点给出了相关设计规定,对于梁柱斜交连接节点并未提及,国外学者对梁柱斜交节点的相关研究成果相对较少。Ball[2]依托Los Angeles国际机场航站楼项目开展了4个足尺斜向骨狗式梁柱连接节点的低周往复加载试验,试验发现此类连接节点的锐角区域应力集中,易断裂,最大节点转角未超过0.04 rad。Kim等[3]采用有限元方法对梁柱斜交节点进行了精细化数值模拟,分析发现连接锐角区域应变需求远大于钝角区域。Hunn等[4]对斜交盖板连接节点进行了系统的有限元分析,研究表明正交连接节点的力学性能明显优于斜交节点,但对于倾角小于15°的斜交节点可忽略角度影响。Mashayekh等[5]对1个足尺正交连接节点和2个25°足尺斜交连接节点进行了低周往复加载试验,研究发现正交连接节点极限转角可达到0.06 rad,斜交连接节点仅达到0.04 rad,通过在钢梁腹板开设斜缝可提高节点的变形能力,但降低了节点的初始转动刚度和抗弯承载力。Hong[6]对焊接骨狗式梁柱连接节点滞回性能进行了数值模拟,分析结果表明对于倾角小于10°的节点仍可按现行规范的有关规定设计。
目前,国内外学者仅对梁柱斜向刚性连接节点进行了初步研究,对于半刚性梁柱斜向连接节点尚未开展研究。基于此,本文对斜向梁柱四角钢连接节点的力学性能进行了探索性研究,重点分析角度对梁柱四角钢连接节点力学性能的影响,进一步研究了顶部钝角及底部锐角单肢弧形角钢的滞回性能,研究成果可为此类节点的工程应用提供参考。
1 角度对梁柱四角钢连接节点力学性能的影响
1.1 模型设计
分析的BASE模型选取钢框架梁柱在反弯点之间的部分,图1给出了BASE模型的几何尺寸。BASE模型的钢梁倾角为30°(倾角指斜梁和水平线的夹角),钢柱采用H型钢,截面尺寸为HW400 mm×400 mm,钢柱长度为3 m。钢梁采用H型钢,截面尺寸为HN450 mm×200 mm,钢梁长度为2.4 m。顶、底单肢弧形角钢截面为L200 mm×12 mm,腹板角钢截面为L110 mm×110 mm×10 mm。BASE模型所有部件的钢材强度等级均为Q235B,部件间采用10.9级M20高强螺栓连接,根据《钢结构高强度螺栓连接技术规程》[7]的要求,施加155 kN预拉力。本次分析共设计了4个不同角度的梁柱斜交四角钢连接节点,具体参数见表1所列。

图1 BASE模型的几何尺寸

表1 模型信息
1.2 有限元模型的建立
BASE模型的所有部件均采用C3D8R实体单元。为更精确地模拟出节点域及连接角钢的力学性能,在梁柱节点区域采用精细网格,在节点的其他区域采用较粗网格。所有接触法向设置为硬接触,切向采用摩擦模拟,摩擦系数0.3。螺栓预紧力采用Bolt load方式分两步施加,第一步先施加100 N的预拉力,确保平稳建立接触;第二步施加155 kN预拉力。图2给出了BASE模型的整体网格划分。

图2 BASE模型的网格划分
材料的本构模型对于有限元仿真分析的正确性至关重要。本文采用Mises屈服准则考虑钢材的弹塑性行为,采用随动强化模型考虑钢材的包辛格效应,采用三折线模型描述钢材的应力应变关系,见图3。其中,fy为钢材屈服强度;fu为钢材极限抗拉强度;εy为钢材屈服应变;εu为钢材极限应变;E为钢材弹性模量;Et为钢材切线模量。对于Q235B钢材,取fy=235 MPa,fu=400 MPa,E=206 000 MPa,Et=0.01E。参考文献[8],对于10.9级高强螺栓,取fy=940 MPa,fu=1 140 MPa。

图3 钢材的应力-应变关系曲线
通过对BASE模型的柱端截面进行耦合,并在耦合点施加铰接约束。通过对钢梁端部截面进行耦合,并建立梁端的局部坐标系,令X=0,为防止钢梁面外失稳,对耦合点沿Y方向施加垂直于梁轴线的位移。图4给出了柱端、梁端的耦合设置。加载制度参考美国SAC(1997)[9]规范,图5给出了具体加载制度。其中,θ为节点转角;N是加载步。

图4 边界条件

图5 加载制度
1.3 有限元模型的验证
为确保有限元分析的正确性,对文献[5]中的25°斜交梁柱连接节点试件S2进行模拟验证。采用上述建模方法建立了试件S2的精细化有限元模型,材料属性、边界约束、加载制度等均与文献[5]一致。图6给出了试件S2的有限元模拟和试验结果的对比。由图6可知,有限元模型可精确评估斜交梁柱四角钢连接节点的滞回性能,数值模拟的滞回曲线与试验曲线吻合较好,进一步证实了本文有限元分析的合理性及可靠性。

图6 试件S2的数值模拟验证
1.4 结果分析
1.4.1 应力分布
图7给出了JD系列模型在节点转角±0.05 rad荷载级别下的应力云图。由图7可知,梁端施加正向位移时,钢梁受拉侧翼缘和钢柱翼缘脱离,另一侧翼缘和钢柱翼缘接触,钝角弧形角钢和锐角弧形角钢短肢大部分区域进入屈服阶段。反向加载时,变形及应力分布状态相反。随着钢梁倾角的增加,钢梁腹板、腹板角钢、翼缘角钢进入屈服的区域扩大,损伤趋于严重,并在腹板角钢和翼缘弧形角钢的中部区域形成塑性区。

图7 JD系列试件的应力云图
1.4.2 滞回曲线
图8给出了JD系列模型的滞回曲线。从中可知,由于翼缘及腹板角钢的张开与闭合,导致JD系列模型滞回曲线的中部出现轻微捏缩,但总体上JD系列模型的滞回曲线仍较为饱满,进一步说明顶、底弧形角钢及腹板双角钢的充分发展塑性。此外,锐角角钢Mises应力明显高于钝角弧形角钢。模型JD-1、JD-2的滞回曲线区别较小,进一步说明当钢梁倾角小于15°时,角度对斜交梁柱四角钢连接节点的滞回性能影响较小。

图8 滞回曲线
1.4.3 骨架曲线
图9给出了JD系列模型的骨架曲线。由图9可知,各试件的骨架曲线呈双线性特征,在弹性阶段,JD系列模型的抗弯承载力迅速上升;在节点进入屈服后,呈现明显的强化特性。钢梁倾角越大,JD系列模型的屈服后刚度越大。钢梁倾角为0°及15°的模型,其正向抗弯(梁由锐角侧向钝角侧转动为正,反之为负)承载力分别为163.23、165.40 kN·m,进一步说明当节点倾角小于15°时,倾角对梁柱四角钢连接节点的力学性能影响可忽略。钢梁倾角为30°和45°的模型,其正向抗弯承载力分别为217.63、251.43 kN·m,比模型JD-1的抗弯承载力增加33.3%和54.0%。此外,对于45°试件JD-3,试件的负向抗弯承载力高于正向抗弯承载力。
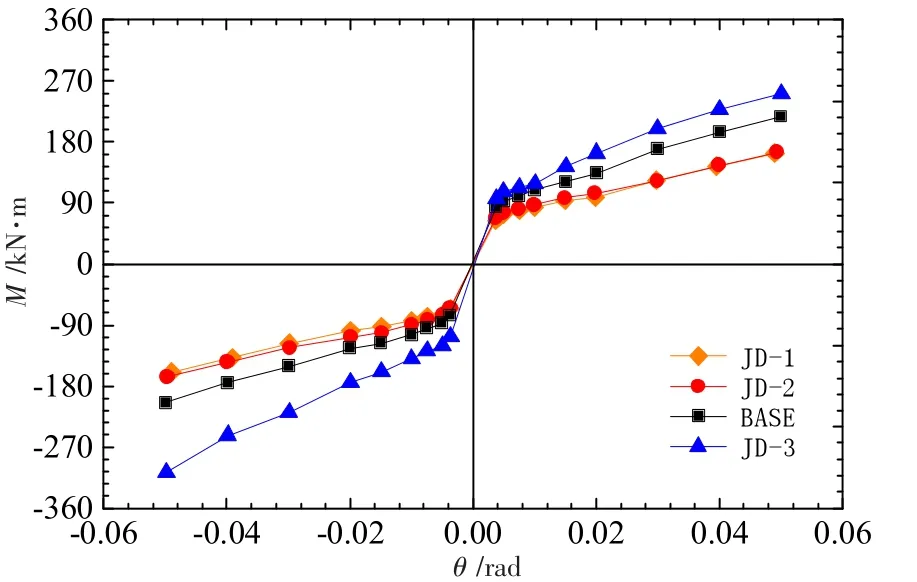
图9 骨架曲线
1.4.4 刚度退化曲线
图10给出了JD系列模型的转动刚度退化曲线。由图10可知,JD系列模型在节点转角达到0.02 rad前,节点的转动刚度退化迅速;在节点转角超越0.02 rad后,节点的转动刚度下降缓慢。在相同荷载级别下,角度越大,节点的初始转动刚度越大。在节点转角为0.037 5 rad时,角度分别为0°、15°、30°、45°的斜交梁柱四角钢节点的初始转动刚度分别为17 480、17 771、21 282、27 122 kN·m/rad,即随着钢梁倾角的增加,节点转动刚度显著增大。特别是在角度大于15°后,节点转动刚度增加尤为明显。

图10 刚度退化曲线
1.4.5 等效黏滞阻尼比
图11给出了JD系列模型的等效黏滞阻尼比。由图11可知,加载至节点转角0.02 rad时,等效黏滞阻尼比达到最大值,分别为0.263、0.247、0.239、0.216。随着角度的增加,JD系列模型的等效黏滞阻尼比呈降低趋势。加载至节点转角0.05 rad时,JD系列模型的等效黏滞阻尼比大于0.18,这充分说明梁柱斜向四角钢连接节点的滞回环仍较为饱满,通过弧形角钢发展塑性提供了较大的耗能,节点具有较好的耗能能力。
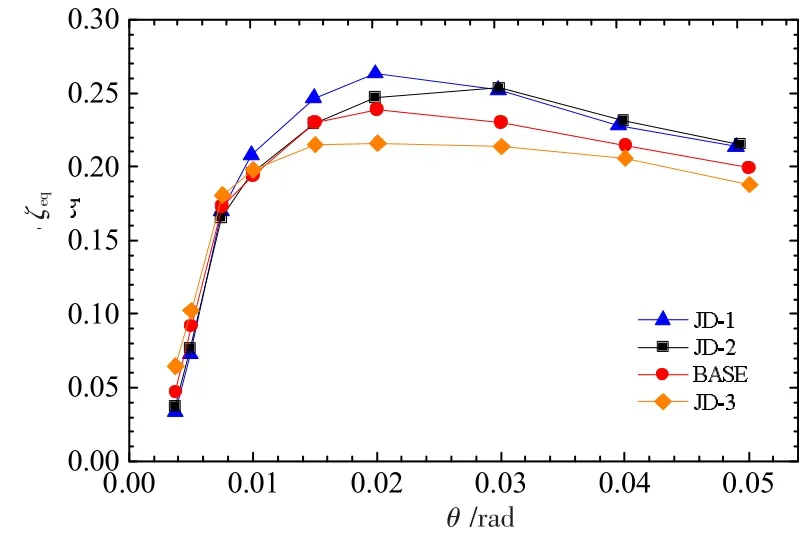
图11 等效黏滞阻尼比
2 角度对单肢弧形角钢力学性能的影响
2.1 模型设计
为进一步评估梁柱斜交四角钢连接节点中的顶、底单肢弧形角钢的力学性能,对顶、底单肢弧形角钢进行独立受力分析。将单肢弧形角钢分别和短柱和模拟钢梁翼缘的钢板连接,在钢板端部施加往复推拉荷载,模拟节点转动过程中角钢的张开和闭合(见图12与图13),角钢与柱翼缘采用2颗10.9级M20高强螺栓连接,与钢梁翼缘采用4颗10.9级M20高强螺栓连接,弧形角钢可由钢板弯折制作。表2给出了单肢弧形角钢BASE模型的详细几何尺寸。在此基础上,分析设计了3个15°、30°、45°锐角和钝角单肢弧形角钢。图13给出了有限元分析的具体加载制度。

图13 单肢弧形角钢的加载制度

表2 单肢弧形角钢BASE模型的几何尺寸
2.2 单肢弧形角钢的有限元模型验证
为确保单肢弧形角钢数值模拟的可靠性,首先对文献[10]的单肢角钢试件L8-58-4进行了模拟验证。本文采用1.2节建模方法建立了试件L-8-58-4的精细化有限元模型,试件的几何尺寸及材料力学性能均与试验一致。图14给出了试件L8-58-4有限元模拟和试验滞回曲线的对比。由图14可知,有限元模拟的滞回曲线与试验结果基本一致,说明ABAQUS程序能够较为精确地模拟单肢弧形角钢的力学性能。

图14 试件L8-58-4的数值模拟验证
2.3 钝角单肢弧形角钢的力学性能分析
2.3.1 应力分析
图15给出0°、15°、30°、45°钝角单肢弧形角钢在极限位移下的应力云图(图中灰色代表钢材屈服)。由图15可知,短柱和钢梁翼缘都处于弹性状态,且Mises应力水平较低,钢柱无明显变形,高强螺栓应力水平相对较高,但尚无明显变形。角钢短肢的大部分区域发展塑性,圆弧段和柱翼缘分离明显。随着角度增加,角钢张角逐渐增大。在达到极限变形时,弧形角钢几乎处于拉直状态。
2.3.2 滞回曲线
图16给出了0°、15°、30°、45°钝角单肢弧形角钢的滞回曲线。由图16可知,四个单肢弧形角钢的滞回曲线呈旗帜形状,且较为饱满,但主要聚焦于第一象限,具有一定的耗能能力。由于角钢张开与闭合导致其滞回曲线在第四象限略显捏缩,且曲线不具有对称性。此外,随着角度的增加,其滞回曲线趋于饱满。

图16 钝角弧形角钢的滞回曲线
2.3.3 骨架曲线
图17给出了0°、15°、30°、45°钝角单肢弧形角钢的骨架曲线。由图17可知,钝角单肢弧形角钢在往复荷载作用下的骨架曲线呈双线性特征,因钢材材料硬化,后期刚度呈现明显的强化特征。随着钢梁倾角的增加,钝角单肢弧形角钢屈服后刚度强化明显,同级荷载下弧形角钢轴向承载力提高明显。

图17 钝角弧形角钢的骨架曲线
2.3.4 轴向刚度
图18给出了0°、15°、30°、45°钝角单肢弧形角钢的轴向刚度退化曲线。由图18可知,单肢弧形角钢轴向刚度前期退化迅速,位移较大时轴向刚度退化均匀、缓慢。对于0°、15°、30°、45°节点钝角角钢的初始刚度分别为49.1、54.6、66.9、81.3 kN/mm,与0°节点相比,15°、30°、45°节点钝角角钢的初始刚度分别提高了11%、36%、66%,钝角单肢弧形角钢初始刚度提高明显。

图18 钝角弧形角钢的刚度退化曲线
2.4 锐角单肢弧形角钢力学性能分析
2.4.1 应力分析
图19给出0°、15°、30°、45°锐角单肢弧形角钢在极限位移下的应力云图。由图19可知,锐角单肢弧形角钢和钝角单肢弧形角钢整体应力水平相当,钢柱和钢梁翼缘均处于弹性状态,角钢短肢的大部分区域弯曲进入塑性阶段。此外,随着角度的增加,塑性区域已发展至角钢水平肢的端部。与钢梁翼缘相连的弧形角钢水平肢并未产生明显变形。
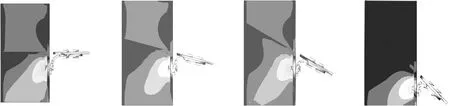
图19 锐角弧形角钢的应力云图
2.4.2 滞回曲线
图20给出了0°、15°、30°、45°锐角单肢弧形角钢的滞回曲线。由图20可知,角度对锐角单肢弧形角钢的滞回环形状有一定影响,四个试件滞回曲线均较为饱满,除0°模型外,随着角度的增加,锐角单肢弧形角钢的滞回环趋于饱满,充分说明锐角单肢弧形角钢塑性发展充分,耗能能力强。

图20 锐角弧形角钢的滞回曲线
2.4.3 骨架曲线
图21给出了0°、15°、30°、45°锐角单肢弧形角钢的骨架曲线。由图21可知,锐角单肢弧形角钢的骨架曲线呈双线性特征,且具有有明显的屈服后承载力。在弧形角钢拉伸位移20 mm时,当倾角由0°增至45°,所对应连接的轴拉承载力分别为164.1、122.4、137.9、169.9 kN,低于具有相同角度的钝角单肢弧形角钢结果。这也是斜向梁柱四角钢连接节点正、负向抗弯承载力产生差异的主要原因。当角度较小时,其轴拉承载力主要由锐角单肢弧形角钢的弯曲提供。当角度较大时,由于弧形角钢的锐角处空间有限,锐角区域角钢短肢长度受限,同时短肢产生竖向轴力,轴拉承载力有所提升。在相同轴拉位移下,锐角单肢弧形角钢的抗拉承载力低于钝角单肢弧形角钢值。

图21 锐角弧形角钢的骨架曲线
2.4.4 轴向刚度
图22给出了0°、15°、30°、45°锐角单肢弧形角钢的轴向刚度退化曲线。由图22可知,四个锐角单肢弧形角钢的初始轴向刚度分别为49.1、42.8、48.4、62.6 kN/mm,锐角弧形角钢的倾斜角度越大,所对应的初始轴向刚度也越大。在相同倾角下,锐角单肢弧形角钢的初始轴向刚度低于钝角单肢弧形角钢结果。
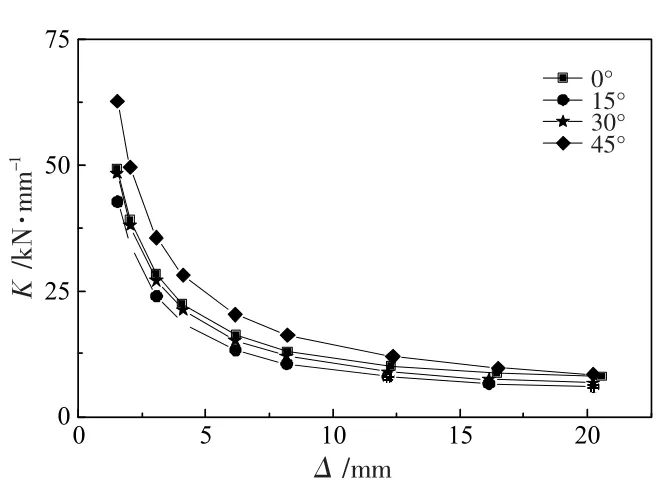
图22 锐角弧形角钢的轴向刚度退化曲线
3 结论
(1)随着角度的增加,斜向梁柱四角钢连接节点的滞回环趋于饱满,其初始转动刚度和抗弯承载力均呈增加趋势;对于角度小于15°时的斜向梁柱四角钢连接节点,可忽略角度影响。
(2)钝角及锐角单肢弧形角钢均具有较为饱满的滞回环,耗能能力较强。除0°单肢弧形角钢外,随着角度的增加,钝角及锐角单肢弧形角钢的轴拉刚度和抗拉承载力均呈增大趋势。
(3)相同轴拉位移下,锐角弧形角钢的轴向刚度和抗拉承载力低于相应角度的钝角单肢弧形角钢结果。
