追求数学本质 探讨合理优化

李瑶晖

前言：“烙饼问题”是人教版义务教育课程标准实验教科书，四年级上册“数学广角”的内容。主要目的是通过一些简单的问题，向学生渗透一些优化的数学思想。笔者在教授烙饼问题时发现，当前一线教学中，部分教师选择直授结论：饼数X3。在咨询了前辈教师之后了解到，烙饼问题由于过于贴近生活实际题型变换复杂，教学中不好操作，学生只能抽象思考难以理解，所以部分教师选择走捷径。

笔者在翻阅大量资料后，利用信息技术制作flash插件，通过新颖课堂模式，让学生“亲自操刀”烙一烙，从而使其可以直观感受烙饼，便于学生理解烙饼的本质，理解“优化”的本质。重点在于，引导学生思考烙饼的本质不是“烙张数”而是“烙面数”。

【教学目标】

1.通过生活中的简单事例，初步体会运筹思想在解决实际问题中的应用。

2.尝试从优化的角度在解决问题的多种方案中寻找最合理的方案，培养分析问题的能力，训练思维的严谨性和周密性。

3.通过各种教学活动，使学生深深地感受到数学与生活的密切联系。

【教学重点】运用优化的方法解决烙饼的问题。

【教学难点】设计烙饼的最合理方案，让学生理解烙饼是烙面数而不是烙张数。

【教学过程】

一、创设情境，引出问题

通过学生熟知的数学荒岛历险记引出故事。

小胖的咔布因为偷吃国王的食物被国王抓走了，罗克必须答对国王的数学题，并且让咔布生产食物送给国王才会放走小胖的咔布。

国王的题目是：国王、数学王子和公主花花每人吃1张饼，平底锅里每次最多只能烙2张饼，两面都要烙，每面3分钟，国王要求必须用最短的时间烙好饼！

你能帮助罗克解决难题么？

提出疑惑，烙饼为什么是数学问题？数学在我们日常生活中处处可见，我们通过数学的思维可以更好地解决日常生活的难题，虽然是烙饼，但其中也确实存在着数学思维。今天我们就一起来研究“烙饼问題”（板书课题）。

二、探究体验，体会过程

（一）提取信息

分析问题，从中找出数学信息。要烙三张饼，一张饼两个面，烙一次3分钟，求最短时间。

（二）实际操作（由简入繁，从简单问题着手）

1、烙1张饼

提出问题：烙1张饼需要多长时间？引发学生思考。将1张饼分为正反面，那么第一次烙正面即正1，第二次烙反面即正2，每次3分钟，一共用了6分钟。学生口述，老师用flash操作，教会大家使用烙饼小程序。

2、烙2张饼

提出问题：烙2张饼需要多长时间？给学生思考的时间。

将2张饼分为正反面即正1、正2、反1、反2，那么第一次烙两张饼正面即正1、正2，用去3分钟，第二次烙两张饼的反面即反1、反2，用去3分钟，一共用时6分钟。学生口述完过程，将黑板右侧的表填完整。

提出疑问：为什么烙1张饼和2张饼所用的时间相同？

3、烙3张饼

提出问题：烙3张饼需要多长时间？学生同桌讨论。

方案一：将3张饼分为正反面即正1、正2、反1、反2、正3、反3，

第一次烙两张饼正面即正1、正2，用去3分钟，第二次烙两张饼的反面即反1、反2，用去3分钟，第三次烙正3，用去3分钟，第四次烙反3，用去3分钟，一共用时12分钟。

方案二：将3张饼分为正反面即正1、正2、反1、反2、正3、反3，那么第一次烙两张饼正面即正1、正2，用去3分钟，第二次烙反1、正3，用去3分钟，第三次烙反2、反3，用去3分钟，一共用时9分钟。学生口述完过程，将黑板右侧的表填完整。

比较两种方案并分析区别：方案一锅里有空余，方案二锅里每次都填满了，得出结论：每次总烙2张饼，别让锅有空余，也就是同时烙，这样最省时间。也就解答了烙1张和2张饼用的同样时间的疑惑。

4、烙4张饼

提出问题：烙4张饼需要多长时间？

将4张饼分为2组，先烙2张同时烙，再烙2张同时烙，一共用了4次，12分钟。

学生口述完过程，将黑板右侧的表填完整。

5、烙5张饼

提出问题：烙5张饼需要多长时间？

将5张饼分成2组，先烙2张同时烙，再烙3张交替烙。一共用了5次，15分钟。

学生口述完过程，将黑板右侧的表填完整。

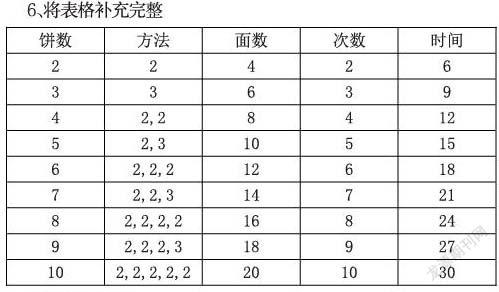
6、将表格补充完整

（三）得出规律

观察上表，你能发现什么规律？学生发言。

1、当烙双数张饼时，两张两张烙就好了;当烙单数张饼时，先两张两张烙，最后再烙三张。

2、每1张饼都需要烙2个面，两张饼有4个面，锅里一次只能烙2张饼，并不是烙完了2张饼，而是烙了2个面。

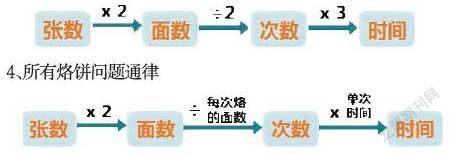
3、本题规律

4、所有烙饼问题通律

三、总结提高

你有什么学习收获？

通过今天的研究，我们知道了烙饼中蕴含的数学思想——优化，数学在生活中处处可见，通过运用数学思维可以帮助我们解决日常生活中的很多问题，希望同学们可以通过烙饼问题的学习，培养优化思维，合理安排时间！