高速长杆弹对有限直径金属厚靶的侵彻分析
2022-04-09赵均海孙珊珊
王 娟,赵均海,周 媛,孙珊珊,吴 赛
(1. 长安大学理学院,西安 710064;2. 长安大学建筑工程学院,西安 710061;3. 长安大学基建处,西安 710064)
长杆弹高速侵彻问题一直是近年来的研究热点[1 − 2],不同于刚性弹,高速长杆弹撞击靶体时,弹靶界面的压力远远超过材料的屈服强度,碰撞应力足以使弹体变形及消蚀[3],关于该问题最初建立的分析模型是流体力学模型,随后此模型被不断改进和发展[4]。Anderson等[5]利用柱形空腔膨胀理论推导了靶体阻力和侵彻速度之间的关系,建立了与时间相关的侵彻模型。国内孙庚辰等[6]通过对弹体头部流动区进行分析,提出了一维简化新模型。兰彬[7]将靶体响应区进行了新的分区,对侵彻模型进行了改进。楼建锋[8]总结了现有长杆弹理论模型,编制了统一计算程序。然而,已有对高速弹体侵彻问题的研究大多是建立在半无限靶体或者有限厚靶体的基础上,未考虑靶体侧面自由边界对侵彻产生的影响,少有的对消蚀弹侵彻有限平面尺寸靶体的探究还主要停留于试验[9 − 10],理论分析则大都忽略了靶体侧面边界的影响,由于当靶体尺寸较小时,这种假设带来的结果与试验偏差明显[9 − 10],蒋志刚等[11]提出了有限柱形空腔膨胀理论,首次以系统的理论建立了长杆弹侵彻有限直径金属厚靶的理论模型,然而该模型只适用于理想弹塑性材料、采用的Mises准则只适合于剪切屈服极限和拉压屈服极限关系为τs=0.577σs的材料,且未讨论侵彻影响因素。随后宋殿义等[12]和王娟等[13]基于此理论进行的靶体侧面边界分析也仅是针对刚性弹,并未对发生侵蚀的高速长杆弹侵彻问题进行研究。
统一强度理论考虑了作用于双剪单元体上的全部应力分量及其对材料破坏的不同影响,可以十分灵活地适用于各种不同的材料[14],包括金属[15]、混凝土[16]、岩石[17 − 18]等,在国内外得到广泛的应用,是求解侵彻复杂应力问题更合理的新强度准则[18]。由于材料强度准则的建立和选用是研究靶材抗侵彻性能的重要环节,同时为了扩大解的适用范围并充分发挥靶材潜能,本文考虑中间主应力的影响,建立基于统一强度理论的有限柱形空腔膨胀模型,推导线性硬化有限直径金属厚靶在弹体高速(1500 m/s~2200 m/s)侵彻时的阻力和深度计算公式;将计算结果与试验结果、其他公式结果对比验证,文献[11]的结果仅是本文结论的一个特例;得到一系列基于不同强度准则的解析解,有效预测了不同靶弹半径比金属靶材的侵深区间;讨论了强度参数、撞击速度及靶体半径对弹道性能的影响,可为金属装甲防护设计提供一定参考。
1 统一强度理论
统一强度理论的数学表达式为[14]:

式中: σ1、 σ2和 σ3分别为双剪应力单元体的三个主应力;α为材料的拉压强度比;b为反映中间切应力及相应面上正应力对材料破坏影响程度的参数,也是选用不同强度理论的参数, 0≤b≤1。
2 基于统一强度理论的有限柱形空腔膨胀模型
2.1 计算模型
有限柱形空腔膨胀模型[11]如图1所示。设柱体半径为rt,t时刻空腔半径为rc(最大值rcf),弹塑性边界半径为rp,r˙c为常数。膨胀过程分弹塑性阶段(rp 图1 有限柱形空腔膨胀模型Fig.1 Finite cylindrical cavity expansion model 由式(1)可得金属材料的等效应力为[13]: 式中, σr和 σθ分别为径向应力和环向应力。 根据线性硬化材料的本构关系,并联立式(3)可得应力-应变关系方程为: 式中:σoy为材料的初始屈服应力; εr和 εθ分别为径向应变和环向应变;E和ν分别为材料的弹性模量和泊松比。 2.2.1 弹塑性阶段(rp 由于应力和质点速度连续[19],由式(6)和式(7),可得: 2.2.2 塑性阶段(rp≡rt) 式中,rc2为第二阶段结束时的空腔半径。 假设 εeq为等效应变, εf为材料单向拉伸断裂应变,基于Hill的塑性功假设[20 − 21]可知: 当rp=rt,第一阶段结束时的空腔半径rc1为: 由式(14)和式(15)可得: 当rc1≤rcf 根据Tate模型方程[22]中: 式中: ρd和 σd分别为弹体的密度和屈服应力;Yd为弹体的特征强度;R为 靶体的阻力;l0和v0分别为弹体的初始长度和速度;l和v分 别为t时刻弹体的长度和速度;u和x分别为靶体侵彻速度和深度。 若rd为弹体半径,取R=A1,rcf可近似取[11]: 若Yd 若Yd>R时,磨蚀先停止,剩余弹体视为刚体,以v=vc2=u侵彻直至v=0 ,vc2则为[11]: 若Yd 式中: 将u=u0,v=v0代入式(17),可求得u0为: 若Yd>R, 总侵深D包括磨蚀侵彻阶段侵深x1和刚性侵彻阶段侵深x2,即: 式中,x1、x2和x1结束时弹体剩余长度l1为[11]: 取文献[9]和文献[10]中试验数据,代入本文公式计算侵深及阻力。文献[9]试验靶板由4340钢制成,密度ρ=7850 kg/m3,弹性模量E=200.6 GPa (Ep=0),泊 松 比υ=0.29,屈 服 应 力σoy=1.365 GPa;钨弹杆长L0=77.9 mm,密度ρd=17 730 kg/m3,特征强度Yd=1.33 GPa,屈服应力σs=1.3 GPa,极限应力σst=1.33 GPa。文献[10]试验靶板为6061-T6511铝合金制成(ρ=2710 kg/m3,E=68.9 GPa,Ep=46 MPa,υ=1/3,σoy=365 MPa);4340钢弹杆长L0=71.1 mm,ρd=7830 kg/m3,σs=1.14 GPa,Yd=σs=1.17 GPa。其他材料参数、试验值和理论计算值汇总见表1所示。 表1 侵彻计算结果汇总Table 1 Summary of calculation results for penetration 图2为当b=0.6时本文公式与文献[9]试验结果、文献公式[9,11]的对比曲线。计算中根据膨胀体所经历阶段分情况运用MATLAB编程计算侵彻阻力及深度。由图2可知:本文公式结果、文献[11]和文献[9]公式结果分别和试验结果对比的平均相对误差为2.00%、5.47%和8.27%;当rt/rd=4.9时,本文结果的最大误差为7.36%,文献[11]的最大误差为10.26%,文献[9]的最大误差可达20%以上,本文结果与试验吻合的最好。 图2 侵彻深度对比Fig.2 Comparison of penetration depth 图3为当b=0.4时本文公式与文献[10]试验结果的对比,两者平均相对误差为3.25%,吻合较好。 图3 侵彻深度对比Fig.3 Comparison of penetration depth 图4为基于文献[9]试验参数的理想弹塑性靶材和线性硬化靶材侵深的比较,当rtr˙c/c≤rcf 图4 不同靶材侵彻深度对比Fig.4 Comparison of penetration depth for different targets 表2为根据本文式(18)、文献[11]和文献[9]公式计算阻力Rt。当rt→∞时,后两者Rt=4.41 GPa,本文公式结果Rt=4.64 GPa,即当本文结论应用于半无限金属靶体时,靶体抗侵彻能力提高了5%。将本文公式应用于文献[10]可得Rt→R∞=1.25 GPa。 表2 不同靶弹半径比时的侵彻阻力计算值Table 2 Penetration resistance of projectiles with different ratios of target radius to projectile radius 图5和图6为b不同时,Rt、Dmax与靶弹半径比rt/rd的关系曲线。由图可知:强度参数b对Rt和Dmax均有较大影响,b值越大,中间主应力效应越明显,Rt越大,Dmax越小。即考虑中间主应力的影响,可以更加客观的表现材料的强度潜能,使构件发挥自身抗侵彻能力,侵彻计算中不宜忽略。 图5 不同b值时侵彻阻力对比Fig.5 Comparison of penetration resistance with different b 图6 不同b值时侵彻深度对比Fig.6 Comparison of penetration depth with different b 不同的材料,b值各不相同,同时b还是选用不同强度准则的参数,当其取不同值时,统一强度理论退化为不同的强度准则,由此所得的结果差别很大,对于金属类材料,采用Tresca屈服准则(b=0)与采用双剪屈服准则(b=1)相比,所得侵彻阻力最大可减小33.33%,侵深最大可增加15.93%。由此说明强度准则的选用对侵彻终点效应的预测也具有重要作用,实际应用中应选择合适的强度准则进行计算,从而更好地合理设计和节约材料。例如本文通过计算,对钢靶取b=0.6时所得结果与试验结果最为吻合,此结果也代表了基于一种新的、针对此靶材更加合适的强度准则的解;若为其它靶材(如铝合金靶材),可取得适合自身的b值进行计算(本文通过计算取b=0.4,与文献[13]一致)。 本文计算方法可以得到一系列解析解,文献[11]所得结果(Mises屈服准则结果)为本文Ep=0、b=0.366 时 的特例(只适合τs=0.577σs的材料);继而得到某一特定工况下弹体侵深的上限值和下限值,有效预测侵彻深度的范围,表3为不同靶弹半径比时金属类靶材侵深的预测区间。 表3 不同靶弹半径比时弹体侵深预测区间Table 3 Penetration depth ranges for projectiles with different ratios of target radius to projectile radius 图7为基于文献[9]试验数据,取Ep=46 MPa时靶弹半径比rt/rd对侵彻深度Dmax和侵彻阻力Rt的影响曲线,由图可知:随着rt/rd的减小,Rt不断减小,Dmax不断增大;当rt/rd<20,Rt/R∞随着rt/rd的减小急剧减小,Dmax迅速增大,rt/rd=4.9与rt/rd=19.88相比,Rt减小了41.30%,Dmax增长了32.61%,此时靶体自由边界对侵彻性能的影响显著,不能继续按半无限靶体进行计算;当rt/rd≥20时,Rt/R∞>0.93,随着rt/rd的增大Dmax减小的速度缓慢,rt/rd=77.66与rt/rd=19.83相比,Dmax只减小了4.19%;当rt/rd≥30时,Rt/R∞>0.97,Dmax相比Rt→R∞时仅增大1.9%。这是由于弹体侵彻靶体的瞬间产生冲击波,该冲击波与靶体产生相互作用,改变波所穿过的靶体介质的材料特性,当冲击波碰上靶体侧面自由边界时,波中的部分能量将被反射回靶体,出现一定范围的靶材破坏响应区,在一定程度上削弱靶体抗侵彻能力;从空腔膨胀理论角度分析,当靶体塑性区域到达侧面边界,边界会向外膨胀,靶体提供的阻力将会变小,弹体所能达到的侵彻深度则变大。 图7 侵彻阻力、侵彻深度与靶弹半径比的关系Fig.7 Relationships among Rt, Dmax and rt/rd. 图8为rt/rd不同时,最终侵深Dmax与撞击速度v0的关系曲线,由图可以看出:v0越大,Dmax越大,当v0≤700 m/s时,Dmax随着v0的增大增长缓慢,而当v0>700 m/s时,Dmax随着v0的增大显著增长。同时,当v0越小,随着rt/rd的减小,Dmax的增长幅度越大,甚至成倍增长,例如当v0=700 m/s时,rt/rd=6.25与rt/rd=19.88相比,Dmax增长了2.04倍。 图8 侵彻深度与弹体撞击速度的关系Fig.8 Relationship between penetration depth and impact velocity 本文采用统一强度理论,研究了较高速长杆弹侵彻有限直径金属厚靶的机理和计算模型,并讨论了弹道终点效应的影响因素。主要结论如下: (1) 采用统一强度理论,建立长杆弹高速侵彻线性硬化有限直径金属厚靶的侵彻阻力和深度计算模型,对半无限金属靶体同样适用。将计算结果与试验、文献公式结果对比,本文结果精确度更高。 (2) 本文方法可以得到一系列基于不同强度准则的解析解,文献[11]结果仅为本文的一个特例。强度参数b对计算结果影响很大,即考虑中间主应力效应,可以更加客观的表现出材料的强度潜能。 (3) 弹体撞击速度v0和靶弹半径比rt/rd对侵彻结果的影响较大。rt/rd=4.9与rt/rd=19.88相比,Rt减小41.30%,Dmax增长32.61%,表明当rt/rd<20时,靶体自由边界对侵彻性能的影响显著,不能继续按半无限靶体进行计算。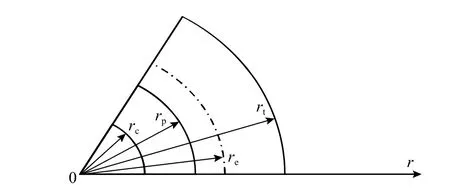
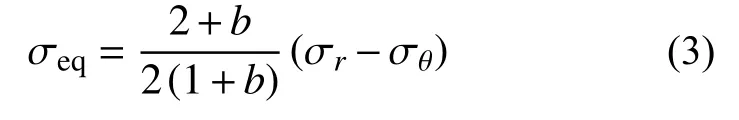
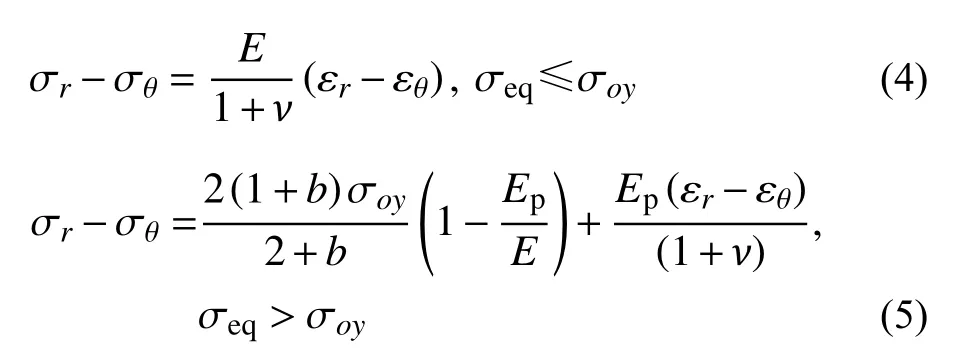


2.2 空腔膨胀应力计算




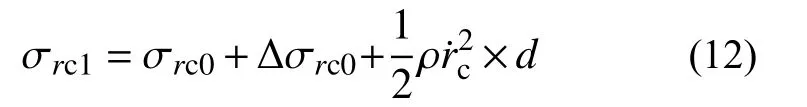

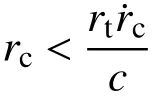
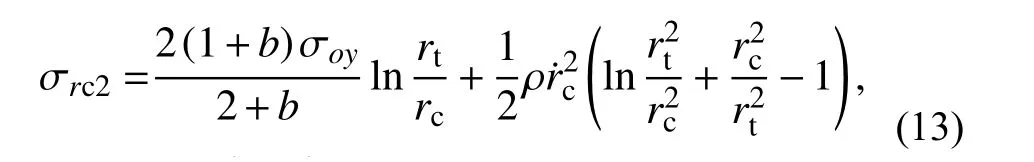


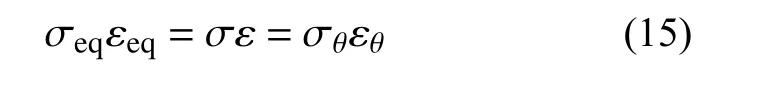
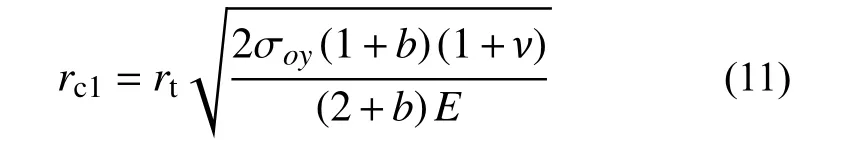



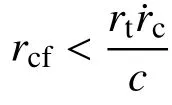
2.3 扩孔耗能和空腔壁平均应力计算






3 长杆弹侵彻有限直径金属厚靶效应
3.1 侵蚀长杆弹侵彻模型分析

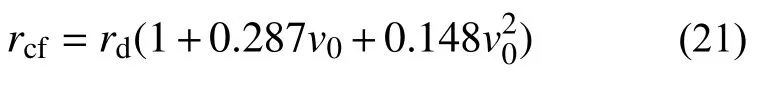

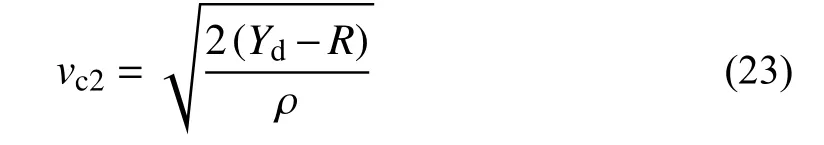
3.2 侵彻深度计算


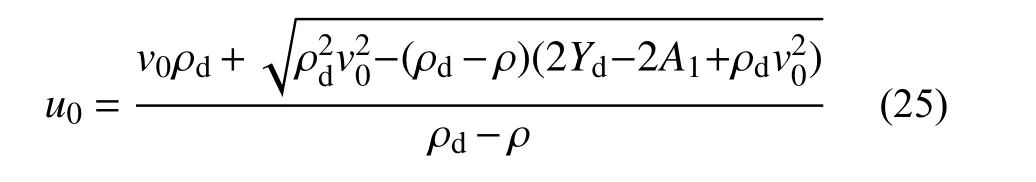


4 算例及讨论
4.1 模型验证





4.2 强度参数的影响



4.3 靶体半径的影响

4.4 撞击速度的影响

5 结论
