CFG桩复合地基有限元模型建立与影响因子分析
2022-04-09湖北省城市地质工程院湖北武汉430000
熊 斌(湖北省城市地质工程院,湖北 武汉 430000)
采用至少两种加固方式,通过桩-桩间土组合加固地基的方式称为复合地基[1]。由水泥、粉煤灰、碎石等构成的CFG桩是一种刚性桩,具有提高地基承载力,减少地基沉降变形,增强地基稳定性的作用[2]。有限元法是研究CFG桩复合地基的一种常用方法,对于分析桩长、桩径、桩间距等参数变化和方案优化具有重要价值[3]。因此,本文对CFG桩复合地基有限元模型建立与影响因子进行了分析。
1 CFG桩复合地基有限元模型的构建
1.1 有限元模型构建方法与步骤
有限元法是一种数值模拟方法,大约在1960年确立和发展起来,实质是将连续的结构离散为有限个结构进行分析,操作步骤[4]为:结构离散化→形函数选择→建立单元应力和节点位移关系→建立单元上节点力和节点位移的关系→建立整体平衡方程→求解未知节点位移和单元应力。
结构离散化是将整体模型分割为有限个单元,例如三角形单元、四边形单元、四面体单元、六面体单元等。形函数表示单元内部节点的位移模式,用矩阵形式表示:(w)=[N](δ)e,(w)为任意点位移的分量列阵,[N]为形函数矩阵,(δ)e为单元节点的位移列阵。单元应力和节点位移的关系可表示为:(ε)=[B](δ)e,其中(ε)为单元内任意点的应变列阵,[B]为应变矩阵,(δ)e意义同前。根据相关物理方程可进一步导出:(σ)=[D][B](δ)e,其中(σ)为单元内任意点的应力列阵,[D]为与材料性质有关的弹性或弹塑性矩阵,[B]、(δ)e意义同前。单元节点力和节点位移的关系可表示为:(F)e=[k]e(δ)e,其中(F)e为单元等效节点力列阵,[k]e为单元刚度矩阵。集合所有单元刚度列阵和等效节点列阵,可建立整个结构的平衡方程:[K](δ)=(R),其中[K]为结构整体刚度矩阵,(δ)为所有单元节点的位移列阵,(R)为总体荷载列阵。根据上面的关系式,界定边界条件,即可求解所有未知节点位移,再根据已求得节点位移计算各单元应变、应力。对于线性问题,可根据各关系式一次求出结果。对于非线性问题,需要经过修正相关矩阵或采用增量法求解。
1.2 有限元建模和分析软件
用于桩-土复合地基建模和分析的常用软件有ANSYS、ABAQUS、MIDAS、PLAXIS等,这几款软件在我国均应用多年,有效性和可靠性得到检验,可用于CFG桩复合地基有限元建模和分析。ABAQUS进入中国较晚,但功能十分强大,尤其在非线性分析方面有其独到之处,采用参数化建模方式,单元种类多,并实现了操作界面中文化,容易满足实际工程的各种需求,因此本文案例采用ABAQUS软件进行桩-土复合地基建模和分析。
1.3 有限元模型的简化处理
完全模拟实际桩-土复合地基,模型将异常复杂,而且要耗费大量计算资源,这样做并无必要,本文对模型进行合理简化,既便于计算处理,又可反映主要特征。假定CFG桩为线弹性体,符合广义胡克定律。地基土、褥垫层为弹塑性体。在施工荷载作用下,地基土物性参数不发生变化。桩、土、垫层为各向同性、单一、均质、连续体。
1.4 本构模型选取
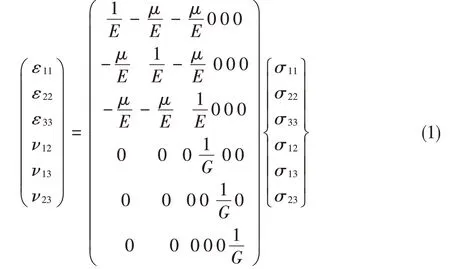
CFG桩符合广义胡克定律,本构模型的应力-应变关系如下:
式中,σij(i,j=1,2,3)为主应力,εij(i,j=1,2,3)为主应变,(νij=i,j=1,2,3)E为切向应变,μ为纵向弹性模量,为泊松比,G为切向弹性模量。
土、垫层本构模型采用摩尔-库仑(Mohr-Coulomb)模型,遵循非关联屈服法则,其函数表达式为:

式中,σ、τ分别为材料的正应力和剪切应力,φ为材料的内摩擦角,c为材料的黏聚强度。
在三轴试验中,主应力σ1>σ2>σ3,则摩尔-库仑屈服准则控制函数表达式[5]为:
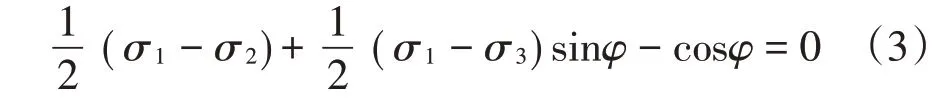
桩-土接触面采用独立模块,接触面的作用有法向和切向之分,法向接触为修正的硬接触,切向接触会产生弹性滑移变形,利用罚(penalty)摩擦计算方法处理。
1.5 参数设置
CFG桩单桩桩径(d)取0.4m,桩长(l)取22m,重度(γ)取24kN/m3,弹性模量(E)取20000MPa,泊松比(μ)取0.15,地基土含水率(w)取21.0%,γ取15.8kN/m3,孔隙比(e)取1.037,粘聚力(c)取22kPa,内摩擦角(φ)取24.1°,压缩模量(Es)取9.70MPa,变形模量(Eo)取29.1MPa,μ取0.25。褥垫层(砂垫层)厚度(δ)取0.2m,γ取20kN/m3,E取50MPa,μ取0.2。承压板(筏板)厚取1m,尺寸取1.3m×1.3m,γ取30kN/m3,E取200000MPa,μ取0.2。桩-土切向作用的摩擦系数取0.41。
1.6 单元选择、网格划分及边界处理
CFG桩、土、垫层、承压板均采用C3D8单元模拟,复合地基设置为正方形,重点考察桩-土接触特性,对桩周侧面的土单元网格进行局部加密处理。桩、土、垫层全局单元近似尺寸(approximate global size)为1.1、0.12和0.12,桩、土全局种子(local seed)为0.08和0.1。以X、Y、Z方向进行U1、U2、U3位移约束。
1.7 初始地应力设置
土体在未受到任何扰动之前,其应力场处于平衡状态,土体重力与相邻土体传递的构造应力大小相等而方向相反。以土体重力与构造应力来观察,由于土体应力状态平衡,位移为零,此即初始地应力平衡状态。创建有限元模型时,若以已沉降固结尺寸来模拟,由于不知道土体原始应力状态,土体在自重应力作用下必然产生变形,影响模型受力分析,数值模拟结果显然不够准确,因此需建立初始应力场,该应力场与地应力(重力)平衡,地基中的应力平衡后便可实现有初始应力但初始应变为零,如此才能在有限元模型上施加工程荷载。
1.8 模型可靠性验证
本文采用单桩进行桩-土复合地基静载试验,并与有限元模型的数值模拟结果进行对比。以200kPa为增量,从零施加荷载至1400kPa,观察地基沉降量。根据试验结果发现,随着荷载增加,数值模拟结果与静载试验的差距逐渐增大,但荷载加至1400kPa时,两者沉降量差距也只有5mm左右,表明有限元模型参数设置合理,为后续研究奠定可靠基础。
2 CFG桩复合地基影响因子分析
2.1 数值模拟方案设计
设计CFG桩复合地基影响因素如下:桩长(l)18m、20m、22m和24m;桩径(d)0.3m、0.4m、0.5m、0.6m;桩间距(s)0.8m、1.2m、1.6m、2.0m;荷载均为1400kPa。
2.2 桩长对桩身竖向应力的影响
2.2.1 单桩复合地基桩长对桩身竖向应力的影响
单桩复合地基桩径(d)均为0.4m,桩间距(s)均为1.2m,而桩长(l)变化,桩身竖向应力(σ)大小也有所差别。例如深度(h)为10m时,l=18m,σ=6.3MPa;l=20m,σ=5.7MPa;l=22m,σ=6.2MPa;l=24m,σ=5.9MPa,如表1所示。考虑桩长一定时,桩身竖向应力随着深度增加而减小,桩顶处竖向应力最大,桩底端竖向应力最小,说明竖向荷载作用在CFG桩上,向桩周土传递的荷载随着深度增加而增加,至桩底端竖向应力不足桩顶应力的1/3。桩长越长,桩底端竖向应力越小,说明桩侧面积越大,可向桩周土传递的荷载越多。
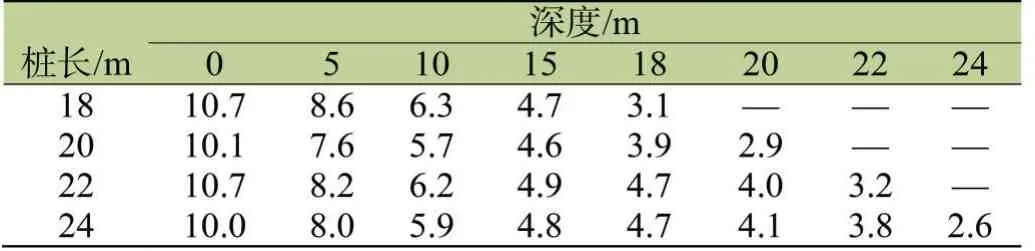
表1 单桩复合地基桩长对桩身竖向应力的影响/MPa
2.2.2 多桩复合地基桩长对桩身竖向应力的影响
多桩复合地基桩径(d)均为0.4m,桩间距(s)均为1.2m,而桩长(l)变化。多桩复合地基桩长对桩身竖向应力的影响,与单桩复合地基桩长对桩身竖向应力的影响有所不同。考虑桩长一定时,随着深度增加,桩身竖向应力先增大再减小,而不是一直减小下去,见表2。这是因为多桩复合地基传递荷载时,存在负摩阻区,即桩身竖向应力最大值以上的深度部分。在负摩阻区,桩周土对桩产生负摩阻力,使地基土中的应力向桩身传递,导致桩身竖向应力出现增大现象,而在负摩阻区以下,桩侧正摩阻力发挥作用,桩身竖向应力也随之减小。桩长变化时,中性点位置也发生了变化。随着桩长增加,中性点位置下移,说明桩长越长,负摩阻区越大。原因在于桩长增加,桩身竖向应力产生的沉降固结效应越明显,土体向桩身传递的应力越多,导致负摩阻区扩大。

表2 多桩复合地基桩长对桩身竖向应力的影响/MPa
2.3 桩径对桩身竖向应力的影响
2.3.1 单桩复合地基桩径对桩身竖向应力的影响
单桩复合地基桩长(l)均为22m,桩间距(s)均为1.2m,而桩径(d)变化,桩身竖向应力(σ)大小差别较明显,见表3。单桩桩径越小,桩身竖向应力越大,例如深度(h)为10m时,d=0.3m,σ=9.9MPa;d=0.4m,σ=6.2MPa;d=0.5m,σ=4.7MPa;d=0.6m,σ=3.7MPa。这是因为桩身竖向应力大小与桩截面积有关,桩截面积越小,桩身受到的应力必然越大,这种情况属于桩的尺寸效应。同样可以看到,在桩径一定的情况下,随着深度增加,桩身竖向应力逐步减小,其原因与本文2.2.1小节桩身传递应力的原理一致。由表1还可以看到,桩径d=0.5m与d=0.6m的桩身竖向应力差距,明显小于桩径d=0.3m与d=0.4m的桩身竖向应力差距,这说明随着桩径的增大,通过增大桩径来减小桩身竖向应力的增益在减弱,换句话说,无限制增大桩径是没有意义的。
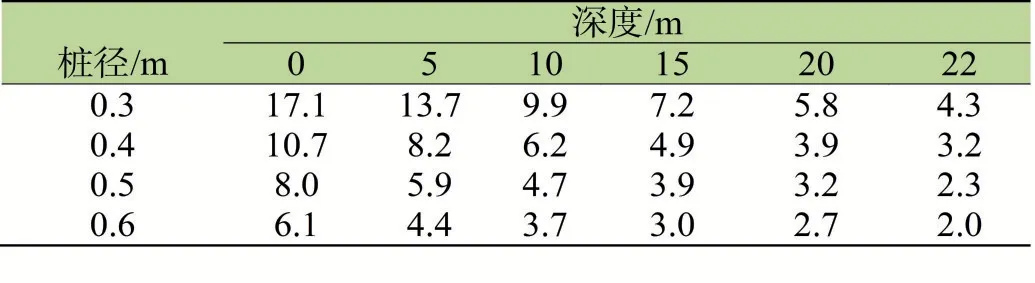
表3 单桩复合地基桩径对桩身竖向应力的影响/MPa
2.3.2 多桩复合地基桩径对桩身竖向应力的影响
多桩复合地基桩长(l)均为22m,桩间距(s)均为1.2m,而桩径(d)变化。与单桩复合地基桩径对桩身竖向应力影响的结果类似,多桩复合地基桩径越大,深度一致时桩身竖向应力越小,见表4。同样可以看到,在桩径一定时,也存在随着深度增加,桩身竖向应力先增大后减小现象,这种特征与单桩复合地基是不同的,原因正如本文2.2.2小节揭示的存在负摩阻区效应一样。通过表4还可以看到,随着桩径增大,中性点所在深度减小,这是因为桩径增大后,多桩复合地基群桩效应的桩-土相对位移有所减小,进而减少了负摩阻区深度。对于多桩复合地基而言,桩径过小或过大都不合适,桩径过小桩身竖向应力太大,容易产生刺入破坏,而桩径过大,难以充分发挥桩的承载力。

表4 多桩复合地基桩径对桩身竖向应力的影响/MPa
2.4 桩间距对桩身竖向应力的影响
2.4.1 单桩复合地基桩间距对桩身竖向应力的影响
单桩复合地基桩长(l)均为22m,桩径(d)均为0.4m,而桩间距(s)发生变化。随着桩间距增大,在深度一定情况下,桩身竖向应力亦随之增大。例如深度(h)为10m时,s=0.8m,σ=3.2MPa;s=1.2m,σ=6.2MPa;s=1.6m,σ=11.1MPa;s=2.0m,σ=15.9MPa,如表5所示。因为桩间距增大,意味着每一根桩承受的荷载加大,因而桩身竖向应力增大。由表5还可看到,桩间距越大,桩身上承受的竖向应力衰减速度加快.例如s=0.8m时,桩顶与桩底端承受的竖向应力差Δσ=5.3-1.7=3.6MPa;而s=2.0m时,桩顶与桩底端承受的竖向应力差Δσ=26.2-5.3=20.9MPa。
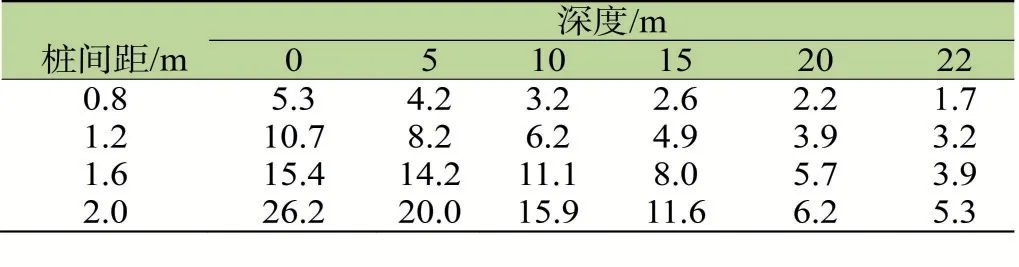
表5 单桩复合地基桩间距对桩身竖向应力的影响/MPa
2.4.2 多桩复合地基桩间距对桩身竖向应力的影响
多桩复合地基桩长(l)均为22m,桩径(d)均为0.4m,而桩间距(s)发生变化随着桩间距增大,在深度一定情况下,多桩复合地基桩身竖向应力同样增大,如表6所示。对于多桩复合地基而言,桩间距增大意味着同样地基面积里桩的数量减小,每一根桩要承担更多的荷载,因而桩身竖向应力增大了。由表6还可看到,当桩间距一定时,随着深度增加桩身竖向应力先增大再减小,说明在深度范围内存在负摩阻区。将表6数据与表5数据进行比较,可以发现多桩复合地基桩身竖向最大应力值大于单桩复合地基桩身竖向最大应力值,因为多桩复合地基桩间土受到强烈压缩,桩-土位移加大,土体产生的负摩阻力增大了应力。
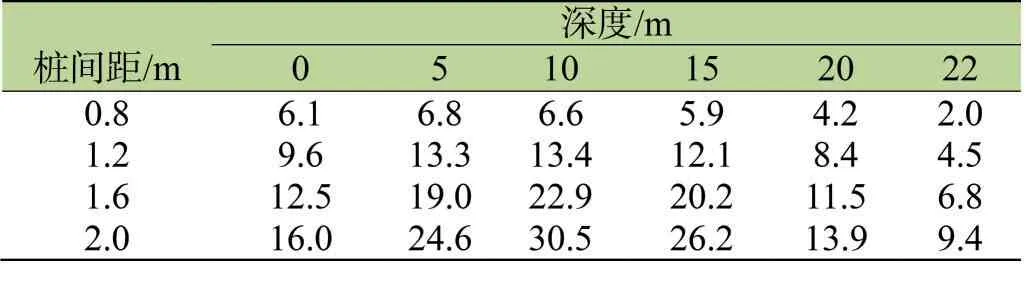
表6 多桩复合地基桩间距对桩身竖向应力的影响/MPa
3 结语
阐述了CFG桩复合地基有限元模型的构建方法,结合数值模拟结果分析桩长、桩径、桩间距三个因素对桩身竖向应力的影响。多桩复合地基存在单桩复合地基没有的负摩阻区,其桩身竖向应力也呈现不同特征,通过对三个因素影响结果的分析有助于CFG桩复合地基的设计和应用。
