基于跳距优化的DV-Hop定位算法
2022-04-09侯华曹俊俊王曹杨沛钊
侯华 曹俊俊 王曹 杨沛钊


摘要:为提高DV-Hop算法的定位精度,该文针对DV-Hop算法存在的跳距误差累计问题提出了一种改进方案。改进的算法从减少误差的产生和扩散两方面对原始算法进行了优化,通过让锚节点以多个通信半径广播信息来降低计算平均跳距时产生的初始误差,同时又让未知节点选择累积误差最小的跳距计算距离,以减少锚节点平均跳距在通信过程中导致的误差扩散。在MATLAB中对改进的算法与原始DV-Hop算法、双通信半径改进算法、跳距加权算法以及跳距修正算法进行了比较,仿真结果表明,改进算法能够最小化定位误差,提高定位精度。
关键词:无线传感器网络;DV-Hop算法;节点定位;通信半径;误差累计
中图分类号:TP393 文献标识码:A
文章编号:1009-3044(2022)06-0004-04
开放科学(资源服务)标识码(OSID):
1 概述
无线传感器网络由随机分布在网络中的大量传感器节点组成[1]。这些节点用来检测周围环境信息并将感知到的数据以及位置转发到被称为汇聚节点的中心位置[2]。节点的定位算法根据其采用的定位方式主要被分为两大类[3]。一类是在定位过程中需要进行测距的算法,这类算法需要通过硬件设备获取到网络中节点之间的距离才能够估计出节点的位置,常见的算法有:RSSI、TOA、TDOA和AOA等。另一类是不需要测距的算法,这类算法主要依靠网络中节点的拓扑结构和连通度来实现,不需要配备额外的测距设备,常见的算法有质心算法和DV-Hop算法等[4]。
传统的DV-Hop算法虽然操作过程简单,但是在定位精度上略显粗糙。然而因其可塑性强的特点,国内外学者提出了大量的改进方案来提高算法的定位精度。文献[5]提出为未知节点所获取的平均跳距都加上锚节点平均每跳误差这一个修正因子,以此来减少锚节点误差对未知节点距离计算的影响,最后使用runner-root算法来求取未知节点的位置坐标;文献[6]中对锚节点使用了两个通信半径,使得节点之间的跳数更加能够反映他们之间的真实距离;文献[7]在算法第二阶段中未知节点将锚节点误差作为权重因子对接收到的多个跳距加权,使每个未知节点获取的跳距都得到了修正,传统算法中节点平均跳距误差大的问题得到优化;文献[8]提出在未知节点获取跳距之后,使用锚节点的单跳误差来修正未知节点跳距中的波动,最后使用LevyPSO算法来求取未知节点的坐标。
上述改进都在一定程度上对DV-Hop算法的定位性能進行了优化,但是该算法仍然存在着不合理跳距导致的误差累计问题。因此,本文希望通过改进算法从误差的源头入手减少误差在通信过程中的扩散,提高定位精度。
2 DV-Hop算法介绍与分析
2.1 DV-Hop算法介绍
经典的DV-Hop算法最大的特点就是不需要测量节点间的距离便可以计算出未知节点的位置信息[9],分为3个阶段对未知节点进行定位。
第一阶段:跳数估计
首先将初始的跳数值设置为0,然后锚节点将自身的坐标和跳数信息打包后向网络中进行广播。在此期间,数据包每经过一个节点,跳数值就增加1。当网络中的所有节点都接收过锚节点传递的数据包后,每个传感器节点都获得了进行通信的最小跳数[10]。
第二阶段:距离计算
使用公式(1)计算锚节点的平均跳距:
[HopSizei=j≠ixi-yj2+yi-yj2j≠ihj] (1)
式中:[xi,yi]和[xj,yj]为锚节点[i]和[j]的坐标,[hj]为锚节点[i]在第一阶段中保存的到锚节点[j]的最小跳数。
使用公式(2)计算未知节点与锚节点的距离:
[dkj=HopSizei×hj] (2)
式中: [HopSizei]表示一个未知节点周围相距最近的那个锚节点的平均跳距,[hj]表示锚节点[j]在第一阶段中保存的到锚节点[k]的最小跳数。
第三阶段:未知节点计算自身的坐标
使用[x,y]表示未知节点的坐标,[xj,yj,j=1,2,……,n]表示锚节点[j]的坐标,再由公式(2)可得方程组:
[x1-x2+y1-y2=d21x2-x2+y2-y2=d22?xn-x2+yn-y2=d2n] (3)
式中:[dj,j=1,2,……,n]表示当前未知节点与各个锚节点之间的估计距离。
对式(3)整理可得:
[A=2x1-xn2y1-yn2x2-xn2y2-yn??2xn-1-xn2yn-1-yn] (4)
[B=x21-x2n+y21-y2n-d21+d2nx22-x2n+y22-y2n-d22+d2n?x2n-1-x2n+y2n-1-y2n-d2n-1+d2n] (5)
[X=xy] (6)
最后通过公式(7)计算出未知节点的坐标:
[X=ATA-1ATB] (7)
2.2 DV-Hop算法误差分析
DV-Hop定位算法的优点在于对硬件设施条件要求不高且计算简单,但是存在定位精度较低的缺点,误差主要表现在以下两方面。
原始算法中,把任意两个通信范围内的节点间的跳数都记为1。如图1中的锚节点B、B1和B2均可在1跳范围内与未知节点A进行通信,根据跳数信息,可以估计出锚节点B1和B2到未知节点A的距离相等,但实际上它们之间的距离是不同的。
传统的DV-Hop算法,未知节点选择距离最近的锚节点平均跳距来计算节点间距离进而得出自身的位置信息,如果所选择的平均跳距存在误差,那么这个误差就会传递给需要计算位置的未知节点,当未知节点计算节点间距离时,这个误差就会得到扩散,导致定位精度的降低。
3 本文改进算法
3.1 锚节点通信半径的选择
由于在传统的DV-Hop算法中所有的节点都有相同的通信半径,导致在通信范围内不论两个节点之间的真实距离如何,估计距离都设为一跳,造成很大的误差。锚节点也会将计算自身平均跳距时的误差传递给未知节点,所以在第一阶段如何降低锚节点在计算自身的平均跳距时所产生的误差是本文所要思考的。
在本文中对锚节点使用了多通信半径的方式来优化所提到的问题。考虑到计算成本,采用了3通信半径,即[R]、[13R]、[23R],其中[R]表示网络中所有节点正常进行通信时的通信半径,其余为锚节点在广播信息时所特有的通信半径。锚节点的3个通信半径将其正常通信范围内的节点分为3组,第一组为当锚节点以[13R]进行通信时,通信半径内的所有节点;第二组为当锚节点以[23R]进行通信时,通信半径内的所有节点;第三组为当锚节点以[R]进行通信时,通信半径内的所有节点。第一阶段锚节点向网络中广播信息时,第一组接收到信息的节点到锚节点的跳数被记为[13],第二组接收到信息的节点到锚节点的跳数被记为[23],第三组接收到信息的节点到锚节点的跳数被记为1。
三组节点之间的关系如图2所示,当锚节点发出信息后,通信半径内的A、B、C三个区域内的节点到锚节点的跳数分别为[13]、[23]和1。第一阶段结束后,网络中的所有节点都记录了相互之间通信的最小跳数,如果这个通信路径中包含有A、B两组节点,那么最终两节点之间的跳数值就有可能出现小数,这就使得跳数的获取更加的精确,从而定位的精度也得到了提高。
3.2 未知节点跳距选择
在传统的DV-Hop算法中,未知节点选择平均跳距时并不会考虑其他锚节点,只会选择距离最近的锚节点跳距。然而在计算锚节点平均跳距时不可避免地产生了初始误差,后续的计算步骤都将使得这个初始误差得到累计,因此如何减少锚节点平均跳距误差的扩散是本文研究的重点。因为误差在估计各个锚节点之间的距离时产生,而锚节点之间的距离大小则会决定误差累计的大小,网络中两个节点的距离越大,它们之间的跳数也会越多,导致误差累计增大。传统的算法针对这个问题的做法是使未知节点选择距离最近的锚节点平均跳距,这样的做法已经尽量避免了误差随着跳数增多的扩散,但这还不是最优的做法。本文中提出来让未知节点选择距离自身累计误差最小的锚节点的平均跳距作为自身的平均跳距,以减少锚节点平均跳距带来的误差累计。
图3中虚线表示两个节点之间的真实距离,实线表示两节点之间的通信线路。A、B兩个锚节点之间的实际距离为25,跳数值为3;A、C两个锚节点之间的实际距离为20,跳数值为4;B、C两个锚节点之间的实际距离为42,跳数为5。通过图上的数据可以计算出三个锚节点各自的平均每跳距离。
[HopSizeA=20+253+4=6.43] (8)
[HopSizeB=42+253+5=8.38] (9)
[HopSizeC=20+424+5=6.89] (10)
表1中展示了图3各锚节点之间的估计距离与真实距离的误差,根据表中数据可以得出锚节点A的平均每跳误差为:[5.71+5.723+4=1.63];锚节点B的平均每跳误差为:[0.14+0.13+5=0.03];锚节点C的平均每跳误差为:[7.56+7.554+5=1.68]。
图3中与未知节点D距离最近的锚节点是节点A,按照传统的做法,未知节点D将使用锚节点A的平均跳距来计算距离,通过这种方式计算出节点B、D之间的距离为[6.43×2=12.86],误差为[20-12.86=7.14];同样根据锚节点A的平均跳距计算出节点C、D之间的估计距离为[6.43×3=19.29],误差为[25-19.29=5.71]。
本文改进的做法中,未知节点D在网络中寻找距离其累积误差最小的锚节点。根据前面的计算数据可得,锚节点A到未知节点D的累计误差为[1.63×1=1.63];锚节点B到未知节点D的累积误差为[0.03×2=0.06];锚节点C到未知节点D的累积误差为[1.68×3=5.04]。显然,锚节点B与未知节点D之间有着最小的累积误差,因此,未知节点将获取B的平均跳距来计算距离,得出 B、D之间的估计距离为[8.38×2=16.76],误差为[20-16.76=3.24]; C、D之间的距离为[8.38×3=25.14],误差为[25.14-25=0.14]。对比发现,改进的做法明显地降低了计算距离时所产生的误差。
3.3 改进算法的具体步骤
Step 1:计算锚节点的坐标并以不同的通信半径向网络中广播它们的位置,邻居节点接收并转发跳数信息。这一过程结束后,所有传感器节点都得到了节点间可以进行通信的最小跳数值。
Step 2:改进的距离估计
1) 假设锚节点[i]和[j]是定位区域中的任意两个锚节点,通过前面的方法可以计算出锚节点[i]的平均跳距为[HopSizei],锚节点[i]与锚节点[j]之间的跳数为[hopij],锚节点[i],[j]的坐标为[xi,yi],[xj,yj]。
2) 锚节点[i],[j]之间的估计距离为:
[dij=HopSizei×hopij] (11)
3) 锚节点[i],[j]之间的距离误差为:
[Δdij=dij-xi-xj2+yi-yj2] (12)
4) 锚节点[i]的平均跳距误差为:
[averHopErri=j≠iΔdijj≠ihopij] (13)
5) 未知节点到锚节点的误差累计为:
[totalHopErrui=averHopErri×hopui] (14)
其中[hopui]表示未知节点[u]到锚节点[i]的跳数。
6) 计算未知节点与锚节点之间的距离:
[dui=HopSizeminErri×hopui] (15)
其中[HopSizeminErri]表示到未知节点[u]累计误差最小的锚节点平均跳距。
Step 3:计算未知节点位置
根据Step 2中的锚节点与未知节点间的距离,使用最小二乘法得出未知节点的坐标。
4 仿真结果分析
使用MATLAB对本文算法与原始DV-Hop算法、文献[5]算法、文献[6]算法和文献[7]算法进行比较。仿真环境为[100m×100m]的方形区域内随机分布着WSN节点,在相同网络条件下分析定位误差,实验结果取仿真100次的平均值。
对定位的结果采用相对定位误差[Er]进行处理:
[Er=i=1Nxi-x′i2+yi-y′i2N×R] (16)
式中:[xi,yi]表示未知节点的实际位置,[x′i,y′i]表示通过改进算法得出的未知节点的位置,[N]表示未知节点个数。
图4所示为当锚节点个数增加时各算法定位误差的变化。固定通信半径[R=30m],未知节点的个数等于200不变,锚节点个数从20到80个不断递增。从图中可得,增加锚节点的个数,各算法的定位误差都在降低。本文改进的算法相较于原始DV-Hop算法在定位精度上有较大幅度的提升,与其他改进的算法相比也有更优的表现。
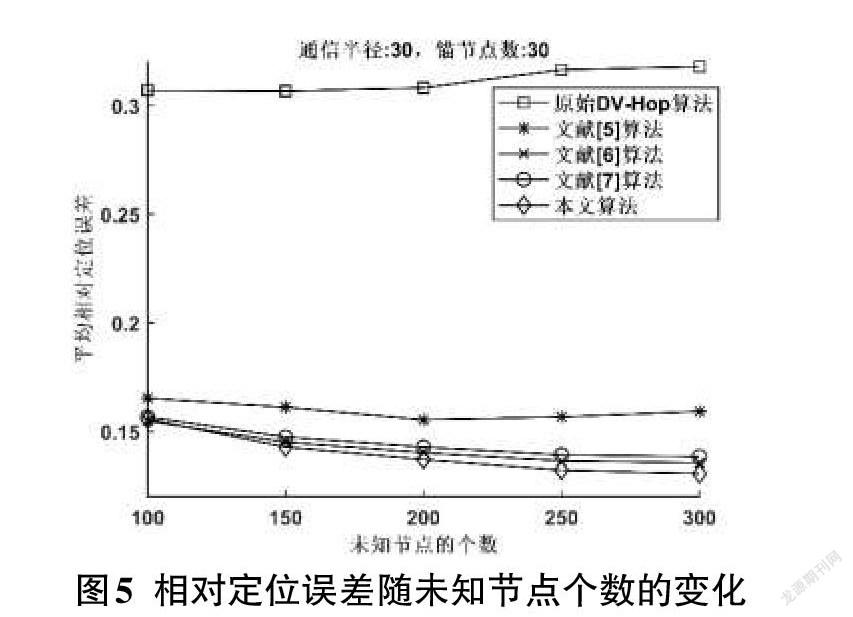
图5展示了未知节点个数增加时各算法定位误差的变化。定位時固定节点的通信半径[R=30m],锚节点个数为30,未知节点个数从100到300不断递增。从图中可以看出,当未知节点的个数小于150时,本文算法与文献[5]和文献[6]的效果很接近,但是随着未知节点个数的增加,本文算法相较于其他算法的优势逐渐显现出来。
图6为相对定位误差随定位区域面积的变化。固定300个未知节点,50个锚节点,通信半径为30m,定位区域为[100m2?200m2]。可以看出当定位区域面积增大时各个算法的定位误差都在显著增加,但是本文改进的算法整体保持最优的定位效果。
5 结论
本文针对DV-Hop算法的误差累计的问题提出了一种改进方案。改进的方案从误差产生的源头出发来降低误差的扩散,在锚节点向网络中广播信息时使用多个通信半径来减少算法的初始误差,在未知节点的跳距选择阶段使得未知节点选择累计误差最小的跳距使用,减少了误差的累计。将改进的算法在锚节点数、未知节点数以及定位区域面积变化的WSN环境下通过MATLAB做了仿真实验。对比发现,本文提出的改进对比传统DV-Hop算法在定位性能上有了明显的提升,与相关的改进算法比较也有更优的定位效果。如何进一步减小定位过程中的累计误差,提高节点的定位准确度,是后续研究的重点。
参考文献:
[1] Mehannaoui R,Mouss K N.A study with simulation of range free localization techniques in wireless sensors networks[C]//2019 International Conference on Advanced Electrical Engineering (ICAEE). Algeria.IEEE,2019:1-4.
[2] WangJ,Hou A Q,Tu Y F,etal.An improved DV-hop localization algorithm Based on selected anchors[J].Computers,Materials & Continua,2020,65(1):977-991.
[3] 吕敬祥,龙满生,尹凯.基于加权最小二乘优化的DV-HOP定位算法[J].传感技术学报,2020,33(3):450-455.
[4] 仇莹,倪晓军.基于牛顿迭代法的DV-Hop改进定位算法[J].计算机时代,2020(9):29-33.
[5] Kanwar V,Kumar A.DV-Hop-based range-free localization algorithm for wireless sensor network using runner-root optimization[J].The Journal of Supercomputing,2021,77(3):3044-3061.
[6] 周涛,蒋占军,路宇挺,等.基于粒子群的DV_Hop算法优化[J].计算机应用与软件,2020,37(3):138-143.
[7] 赵芝璞,吴栋,王艳,等.基于平均跳距和位置优化的改进DV-Hop定位算法[J].系统仿真学报,2016,28(6):1273-1280.
[8] 檀爽,毛永毅.基于最优跳距和LevyPSO算法的DV_Hop定位算法[J].传感技术学报,2018,31(6):927-931.
[9] Niculescu D,NathB.Ad hoc positioning system(APS)[C]//GlobalTelecommunications Conference,San Antonio,TX:IEEE,2001:2926-2931.
[10] Kumar S,Lobiyal D K.Novel DV-Hop localization algorithm for wireless sensor networks[J].TelecommunicationSystems,2017,64(3):509-524.
【通联编辑:代影】
