动车运用所调车作业计划优化
2022-04-08范贤徐小明钱程
范贤,徐小明,钱程
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
为保证动车组列车的安全稳定运行,动车组列车采用预防修的方式进行检修。为了安全高效地完成动车组的检修任务,动车运用所需要根据动车组的运用计划,提前制定调车作业计划。随着高速铁路的快速发展,动车组的检修任务快速增加,动车运用所的检修能力成为制约高铁运营的重要因素,提高运用所的检修能力对于高铁运营具有重要意义。动车组检修工作是保障动车组列车安全运行的关键,当前动车所面临的检修压力不断增大,以全路规模最大的动车所——上海虹桥动车所为例,日均检修量达到64~75组[1]。除了扩建动车运用所,制定高效合理的调车作业计划成为提高运用所检修能力最直接、快速和廉价的方案。此外,目前很多动车运用所还是采用手工的方式编制调车计划,不但效率低、质量难以保证,而且随着检修任务的增加,手工编制调车计划将变得越来越困难。
动车运用所调车作业计划问题是随着高速铁路发展而出现的铁路优化方面的新问题。Caprara等[2]对客运铁路的相关问题进行了总结和回顾,其中列车单元调车问题(train unit shunting problem, TUSP)与动车运用所调车作业计划问题有很多关联性。
列车单元调车问题是在给定列车时刻表的条件下,确定到发列车的解编、编组和在存车线的存放方案,使得列车单元运用无冲突,且成本最小。Freling等[3]将列车单元调车问题分解成列车单元匹配问题和列车单元停放问题两个子问题分开求解。Kroon等[4]提出了一个新的模型,综合考虑了列车单元的匹配和停放问题。Haahr等[5]运用三种不同的算法求解列车单元调车问题,并测试了不同算法的性能。Lentink等[6]提出了一个更加完整的列车单元调车问题,还包含列车单元的路由和路由成本计算这两个子问题。
Jacobsen等[7]研究了检修场内的列车调车计划问题,该问题更多地考虑了检修资源(如检修设备、检修人员等)的约束。Tomii等[8]研究了站台的列车调车问题,一种简化的列车单元调车问题。因为列车不需要解编,且存车线上只能同时停放一组列车。之后,Tomii等[9]在此基础上进行了扩展,考虑了列车的检修、清洗等任务的调度和场站工作人员的排班。
由于铁路系统的差异,当前对运用所调车作业计划问题的研究主要集中在国内,大多采用启发式方法求解。王忠凯等[10]较早地对该问题进行了研究,以检修流程要求和股道布局等为约束条件,以减少对洗车线等稀缺资源的占用和调车费用最低为目标建立模型。郭小乐等[11]以动车组在动车运用所内的总延误时间最小为目标。童佳楠等[12]考虑了检修线为双列位的情况。王家喜等[13]以最小化调车总钩数为目标,重点考虑了进路冲突约束。殷迪等[14]将调车作业计划编制问题转化为带有不定加工时长的车间调度问题。韩宝明等[15]研究了加入人工洗车的调车作业计划问题,使更加接近动车运用所的实际。
综上所述,动车运用所调车作业计划问题相比于列车单元调车问题更加关注列车在各个线区的作业和流转,需要对场站设施进行更加微观地建模。一些既有文献对动车运用所的进路冲突考虑不足,导致编制的调车计划无法应用于实践。另外,随着检修规模扩大,许多方法由于计算时间过长等原因,不适用于实践应用,因此开发一种快速的求解算法显得格外重要。
本文针对动车运用所一级检修的调车作业计划编制问题,考虑检修流程、股道占用、进路冲突等约束,以所有动车组完成检修任务的时刻之和最小为目标,建立优化模型,设计基于贪婪和邻域搜索的启发式算法进行求解,并开展算例分析,验证算法的有效性。
1 问题描述
图1所示是一种典型的尽端式动车运用所的布局,包括检修线区、洗车线区、存车线区和咽喉区的运用所出入线。每个线区有若干条作业股道,不同作业线区通过调车股道连接,动车组通过调车股道在不同的线区流转。

图1 典型的动车运用所布局
一级检修主要包含检修作业和洗车作业两项作业工序,完成这两项作业后,动车组的检修任务结束。动车组检修作业工序一般不固定,但因为未洗车而直接进行检修作业对检修车间的环境有较大影响,所以动车运用所一般倾向于采用先洗车后检修的作业顺序。同时,存车作业并不是必须的,是否需要存车作业取决于洗车线和检修线的占用情况,以及动车组完成所有的检修作业时距离出所的时间之差。例如,当检修线区和洗车线区的作业轨道都被占用时,新到运用所的动车组只能进行存车,等待检修;当动车组完成所有检修任务后,如果距离运用计划中的下一个营运任务的时间较早,也需要进行存车,等待出所执行营运任务。在极端情况下,动车组可以在无存车作业的情况下完成所有检修任务后离开动车运用所。调车作业计划问题是在已知待检修动车组的入所和出所的时间的条件下,根据运用所检修设施的具体布局,结合检修流程等检修规范,进路冲突、股道占用等实际约束,确定需要检修的动车组在存车线、检修线、洗车线等功能线区上的路由和停留方案,即确定检修动车组各项检修作业的顺序、检修作业的起始和终止时刻以及占用的作业线,使得动车组能够在规定时间内完成检修计划中规定的检修内容。
在动车运用所调车作业计划问题中,对检修和洗车线区的利用率能够反映出调车作业计划的质量,对作业线区的无效占用越少,调车作业计划的质量越高。王家喜等[14]以最小化调车钩数为目标进行求解,但是调车钩数只能从侧面反映出检修流程的优劣,不能直接反映调车计划对检修线和洗车线等关键线区的占用情况。本文中,我们以所有动车组完成最后的检修任务,开始调车离开作业线的时刻之和最小化为目标进行求解。
2 优化模型
本节中,我们将对动车运用所调车作业计划问题构建模型。为了简化问题和求解方便,我们做出如下假设:
(1)已知每一列动车组的入所和出所的时间;
(2)入所的动车组都需要进行一级检修,包括洗车作业和检修作业,两项作业的执行顺序不固定;
(3)动车组洗车作业需要的最小作业时间相同且固定,与动车组无关;
(4)动车组检修作业需要的最小作业时间相同且固定,与动车组无关;
(5)动车组调车作业需要的作业时间都是相同且固定的,与调车作业涉及的作业轨道无关。
2.1 模型参数
表1列出了本文模型中所用的参数符号。

表1 参数符号及其定义
2.2 模型表达
上文提到,对检修和洗车线区的利用率反映出调车作业计划的质量,减少对洗车线和检修线的无效占用能提高检修效率,因此,提高调车作业计划的质量需要最小化动车组对作业线的占用时长,如式(1)所示:
(1)

(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
模型中,式(3)表示动车组在作业线f上的检修顺序约束;式(4)表示动车组k执行各项检修作业的顺序约束;式(5)为作业r在作业线上的最小停留时长约束;式(6)为动车组k完成所有检修作业时刻的约束;式(7)为作业线f占用的时空相容性约束,即当作业线f上的作业j紧接着作业i执行,那么作业j的开始时间大于作业i的结束时间;式(8)为动车组k检修作业顺序的时间约束,即当动车组k的作业j紧接着作业i执行,那么作业j的开始时间大于作业i的结束时间;式(9)为作业线数量约束,作业线上第一个作业(或最后一个作业)之和等于作业线的数量;式(10)为检修动车组数量约束,动车组执行的第一个作业(或最后一个作业)之和等于动车组的数量;式(11)为动车组开始检修的时间晚于动车组入所时间的约束;式(12)为动车组检修结束的时间早于动车组出所的时间的约束;式(13)为决策变量的取值范围约束。
由于存车作业在数量上和时间上具有的灵活性,考虑存车作业将使得模型构建变得困难,同时存车线区并不是动车运用所的瓶颈资源,因此在该模型中不考虑存车作业,对问题进行了简化处理。本文需要解决的是完整的调车作业计划,即包含所有检修、洗车、存车和调车作业占用的作业轨道和时间。该模型只考虑了检修作业和洗车作业对作业线的占用,因此模型的解不是完整的可行解,仅包含检修、存车和相关的调车作业。具体来说,对于每一组动车组,在该动车组的检修流程中,在检修作业之间和在所有的检修作业完成之后插入存车作业,并安排具体的存车作业线,保证存车作业线的时空占用相容,以此得出一个完整可行的调车作业计划。
3 求解算法
动车运用所调车作业计划问题是确定动车组的检修作业顺序和检修作业的开始结束时间,同时将检修作业分配到相应的作业线上,满足作业线的时空占用相容性等约束。由于本文提出的模型为简化问题后的模型,得出的解并不是完整的调车作业计划,因此我们提出了一种两阶段的启发式算法对该问题进行求解。第一阶段通过贪婪启发式算法求出初始解,第二阶段通过对初始解进行邻域搜索来优化初始解。
3.1 贪婪算法
采用贪婪算法,通过模拟动车组在动车运用所的检修流程来获得初始解。考虑到实际调车计划的编制一般以分钟为单位,同时为了减小求解的复杂度,本文以分钟为单位,将检修规划周期离散化。例如,规划周期为16 h,则可以划分为960 min。任意一条作业线在任意一个时刻都对应一个状态,表示该作业线处于空闲状态或者被动车组占用。
存车作业并不是动车组检修的必要作业,只有当检修线和洗车线都被占用,或者动车组完成所有检修作业的时刻早于离开动车运用所的时刻时才需要进行存车。所以为了减少检修流程的时间,应尽量减少不必要的存车操作,同时考虑到未洗车动车组对检修作业和检修车间环境的影响,动车运用所一般倾向于先洗车后检修的作业顺序,但为了加快检修的速度,此顺序并不是固定的。在求解开始时,首先按照入所时间的先后顺序对动车组进行排序。动车组的检修流程如图2所示。

图2 动车组检修流程图
(1)当动车组到达运用所时,依次检查洗车线是否空闲,如果有洗车线空闲,将动车组调至该洗车线进行洗车;
(2)如果没有洗车线空闲,依次检查检修线是否空闲,如果有检修线空闲,将动车组调至该检修线进行检修;
(3)如果洗车线和检修线都被占用,那么调至存车线进行存车,同时时刻监视洗车线的占用情况,一旦有洗车线空闲,立即调车至洗车线进行洗车;
(4)洗车作业结束后检查是否有检修线空闲,如果有,调车至检修线进行检修,检修完毕后调车至存车线等待发车出所;
(5)如果没有检修线空闲,那么进行存车作业,同时时刻监视检修线的占用情况,一旦有检修线空闲,立即调车至检修线进行检修。检修完毕后调车至存车线等待发车出所。
需要注意的是调车作业对作业线的占用。调车过程中需要占用咽喉区的进出作业线,所以同一时刻只能有一项调车作业进行,同时,调车的过程中也会同时占用当前作业线和调车的目标作业线。另外,本文不考虑动车组出入所的调车作业。
3.2 邻域搜索
邻域搜索是一种求解最优化问题的启发式算法,从初始解开始,通过在当前解的邻域中寻找更优解并更新当前解,不断迭代地寻找更优解,直到满足算法终止准则。本文采用的邻域搜索算法如下:
Step 1 通过贪婪算法得到初始解s,并令sbest=s;
Step 2 对s进行邻域操作,即从s的邻域N(s)内取解s′,使得目标函数值f(s′) Step 3 如果存在这样的解s′,那么令s=s′,sbest=s′,转到Step 2; Step 4 否则,算法结束。 本文定义以下两种邻域操作: (1)插入作业操作。给定两条相同类型的作业线,将其中一条作业线上的一个作业插入到另一条作业线上的任意位置。 (2)交换作业顺序。给定一条作业线,选择作业线上的两个作业,交换这两个作业的执行顺序。 在进行邻域操作后,我们得到了一个新的解,新解对应的检修方案和目标函数值参考求初始解的贪婪算法求得,具体如下:首先,根据动车组的入所时间和动车组在洗车线上的作业执行顺序确定动车组在洗车线上的作业的开始和结束时间。随后,同时考虑入所时间,洗车作业的开始、结束时间和动车组在检修线上的作业执行顺序确定检修作业的开始结束时间,即当动车组的入所时间和洗车开始时间之间的时间满足检修用时,且不与其他动车组的检修时间冲突时,先安排动车组进行检修;否则,在洗车后进行检修,并根据洗车结束时间和检修线上一个作业的结束时间确定该动车组检修的开始和结束时间。注意,如果邻域操作得到的解是不可行解,则放弃该解。 本节以图1 中的横向尽头式的动车运用所为基础开展算例研究。该动车运用所有检修线4条,洗车线2条和存车线9条。调车计划规划周期从下午4时开始,到第二天上午8时结束,共计16 h,将时间离散为以分钟为单位,共960 min。表 2 为动车组运用计划,其中,出入所的时间以分钟为单位,并以下午4时为0时刻计算。 表2 动车组运用计划 4.2.1 普通算例的结果及分析 本文假设同一种类型的作业的最小用时都是相同的,与作业的股道和执行作业的人员无关。假设检修作业最小用时90 min,洗车作业最小用时30 min,调车作业用时5 min。本文算法通过C#编程实现,在内存为16 GB,CPU为i7-4710HQ的计算机上运行,运行时间小于1 s。表 2 中的普通算例的结果如表 3所示。表中W1(0~30)中,W1表示对应的作业线,括号内数字为动车组在作业线上的开始和结束时刻,作业之间的时间间隔表示调车作业用时,其他符号含义类似。 表3 动车组在运用所的检修方案 求解过程中发现,对于上述算例,邻域搜索并不能改进初始解。分析动车组在运用所的检修流程后发现,动车组入所后即开始检修任务,且检修过程中没有额外的存车作业。 对算例进行进一步分析,最优的检修流程为:洗车—调车—检修—调车—存车,目标函数不包含最后的调车和存车用时,那么一组动车组最小占用作业线的时长为洗车、调车和检修的最小用时之和,因此,解的下界可以通过动车组的入所时刻加检修流程最小用时求得。对于上述算例,所有动车组的入所时刻之和为3 610,一组动车组检修流程最小用时为一次调车作业、一次洗车作业和一次检修作业的最小所需用时之和,即125,那么目标函数解的下限为3 610+125×15=5 485。因此,初始解即为最优解。 4.2.2 动车组集中入所算例的结果及分析 如果出现动车组集中入所的情况时,动车组在入所时和检修过程中由于检修作业线都被占用,将不可避免地出现存车作业。因此我们在表2算例的基础上设计一个特殊的算例,如表4所示。该算例中,动车组将会在300~500之间(即当日21:00到次日0:20)集中入所,此时会出现作业线被全部占用的情况。 表4 特殊设计的动车组运用计划 在该算例下,最优解的下界为6 850,贪婪算法得到的初始解为6 985,对初始解进行邻域搜索后的解为6 975,邻域搜索后的解相比初始解可以减少总计10 min的检修用时,详细的调车计划如表5所示。 表5 初始解和邻域搜索优化后的动车组检修方案 详细分析两个解的调车计划可以发现,邻域搜索后的解相比初始解减少了两次存车作业,即动车组EMU14和动车组EMU15各减少了一次存车作业。但是由于检修过程中的存车作业具有灵活性,因此减少存车作业次数并不一定减少对作业线的占用时长。例如,EMU15虽然减少了一次存车作业,但是总的存车时长没有减少,因此完成所有检修任务的时间并没有减少。邻域搜索算法虽然对解的优化有限,甚至没有优化,但在求解过程中可以得到多组不同的解,在实际应用中,可用于改善动车组检修作业的流程,或为调车作业计划编制人员提供决策支持。 表6 不同规模算例的测试结果 对于15组动车组的算例,随机生成的5个算例中,有3个算例直接通过贪婪算法就能求出最优解,另两个算例的解的Gap值也较小。邻域搜索对该规模下的算例作用有限,只有一个算例有0.82%的改进,表明了本文提出的贪婪算法求得的初始解即为较好的解。对于20组动车组规模的算例,动车运用所的检修资源变得更加紧张,检修流程中存在多余的存车作业,Gap值明显增大。在该规模下的算例,邻域搜索取得了较好的效果,5个算例中,有4个算例对初始解有不同程度的优化,平均优化1.35%。算例测试表明所提出的算法能有效求解本文问题。 本文以动车运用所的股道布局、股道时空占用相容性和检修作业要求等为约束,以最小化完成动车组所有检修任务的时刻之和为目标,将动车运用所调车作业计划问题构建为0-1整数规划模型。由于模型的解并不是问题的完整可行解,因此设计了结合贪婪策略和邻域搜索的启发式算法。算例分析表明,基于贪婪策略的初始解算法能快速地得出较好的初始解,甚至能直接求出最优解。 本文研究的动车运用所同一时刻只允许一组动车组调车,所以调车作业进路冲突问题容易解决,但当动车运用所规模较大,进路复杂时,调车进路冲突问题将是一个值得研究的问题。同时,如果检修动车组数量继续增加,当前的算法可能不能保证得出可行解,对于大规模算例的算法改进也是值得研究的一个方向。4 算例分析
4.1 算例设计
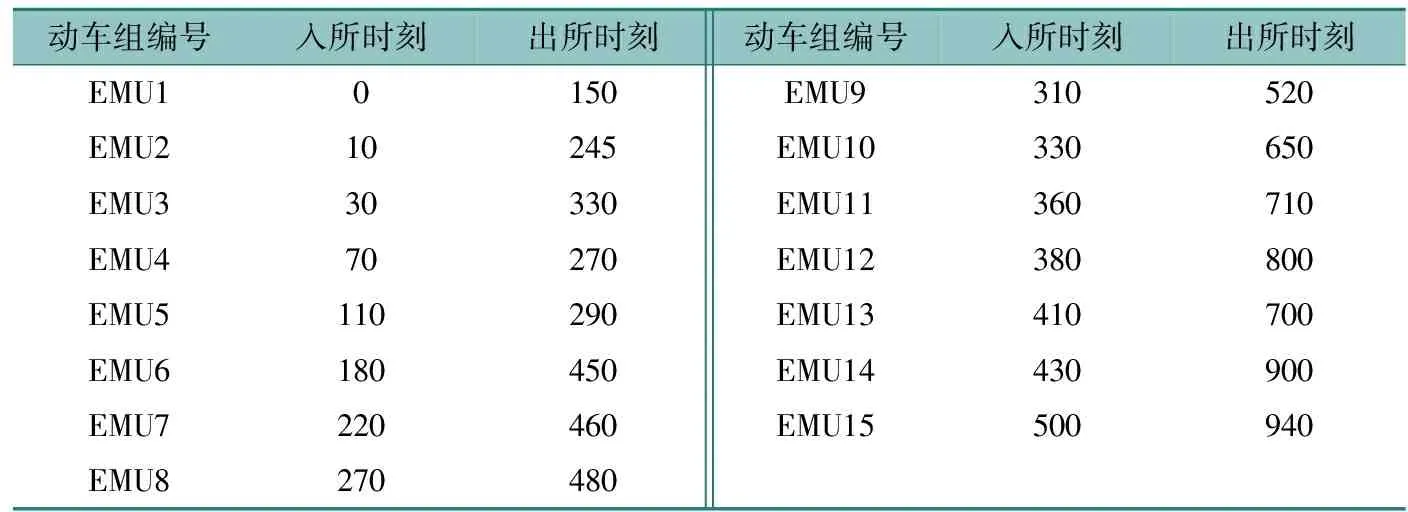
4.2 算例结果及分析



4.3 算法可靠性测试


5 结论
