空气中声速随温度变化规律的简易实验
2022-04-08郭中华
罗 京,郭中华
(兰州城市学院 物理系,甘肃 兰州 730070 )
声速的测量在声学检测、超声应用研究方面非常重要,也是大学物理实验教学中的一项基础实验. 在实验室条件下,声速的测量方法主要有驻波法和相位比较法,通常采用信号发生器、示波器、压电陶瓷换能器等实验仪器,计算声波的波长、频率进而得到声速[1-3]. 驻波法是基于驻波的形成原理,易于理解、便于测量,但实际测量中存在多级反射波的叠加;相比之下相位比较法利用入射端与接收端波在介质中传播的相位差形成李萨如图形来测量,结果较为准确,但相位的测量易受介质性质的影响.
这两种方法中,驻波法利用了声波遇到硬边界反射与入射波叠加而形成驻波的原理,相关的实验理论及讨论较多[4-6]. 而对于软边界,亦存在反射波,频率满足一定条件也可与入射波叠加形成驻波,并可依此来测量声速,但其实验设计较少,文献中对其理论的分析不够完整. 此外,空气中的声速是和温度有关的,声速随温度的变化规律在一些实验设计中也有效的实现了控制. 比如买买提等利用空调改变室内温度[7],冯升同、郭立群等利用单片机内的高速输入电路外接电阻丝加热石英玻璃管等相关元件改变管内空气的温度[8,9],但这些方法存在实验时间较长、易受实验条件限制及有一定危险性等问题.
由于突如其来的疫情影响,线上教学普及开来,教育部及时针对大学物理实验课程提出了指导性方案[10]. 设计在非实验室环境下能完成的简易物理实验,丰富在线教学实践,让更多人获得居家自主学习的体验,这不仅对于某些特殊时期的线上教育有重大意义,更为自然科学知识的普及和推广提供了良好的平台. 在驻波法测量声速的基础上,本文分析了两端开口管中驻波的实现原理,并借助生活中一些常见的器材,如智能手机,实现声波的发射和频率的测量,电阻丝加热薄不锈钢管来改变管中温度,研究空气中声速随温度的变化规律. 这种简易装置实现方便、现象直观,重在理解物理现象背后的理论,契合居家物理实验的自主学习目标,并对培养学习者的实验素养很有助益.
1 驻波法测量声速的基本原理
图1为两端开口管中声波传播示意图,声波从管的一端传播到另一端时,管的截面发生突变,使声波传播过程中的边界条件发生变化,可引起声波的反射而形成驻波[11]. 选取一段有限长、截面均匀的直管,长度L=40 cm,管口直径d=2.5 cm,在传入管中声音的频率范围内,声波的波长远大于管的口径,因此管中声波可视为平面波.设一列平面声波传播到两种分界面处,其入射波和反射波的形式为
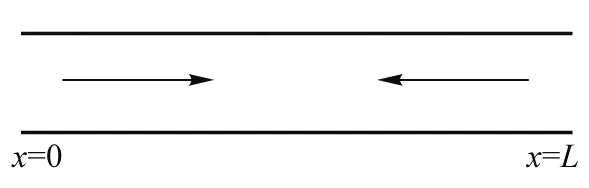
图1 管中声波传播示意图
pi=pi0exp[i(2πνt-kx)],
pr=pr0exp[i(2πνt+kx)]
(1)
根据声波的叠加原理,合成声场声压为
p=pi+pr=2pr0coskxei2πνt+[pi0-pr0]ei(2πκt-kx)
(2)

在管的末端,声压遇到截面的突变,其声场复杂,传播介质受到压力影响会对声波的传播产生阻碍,称为阻抗.在分界面处反射和透射的大小就取决于介质的特性阻抗z=ρu,ρ为介质密度,u为介质中声速.如图2所示,管口处界面发生变化,S1和S2分别为管口两侧的截面积,设界面声压反射系数为
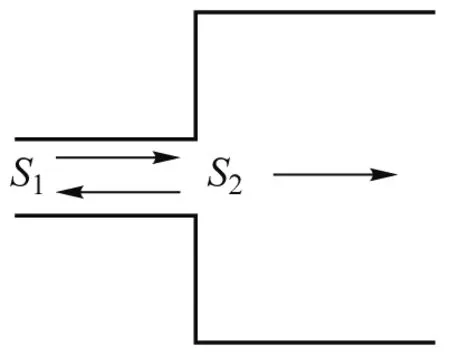
图2 管口处截面的变化
(3)
根据管中合成声压可求得管中介质质点速度,并可进一步得到管中的声阻抗[11],由此获得长度为L的有限长管中输出声阻抗为
(4)
z(0)为输入端的声阻抗.声波从入口端向右传播进入开口端时与大气耦合,大气辐射声阻抗会使一部分声波返回.由于管的孔径较小,在声音输出端声阻抗约为零,则由式(4)得到
(5)

(6)
当n=1,2,3,…时,分别对应管中基频和各阶谐频.因此,从式(6)测得同一开管中产生驻波的相邻两声波的频率差,就可求出声速u,即
u=2L(νn+1-νn)
(7)
利用式(7),只需要测量开管的长度和相邻本征振动的频率值,就可以计算出声波在空气中的传播速度.
严格来说,声速的大小与传播介质有关,既与介质的本身属性(密度、模量)有关,又与外部状态量(温度、压强)有关.而对于干燥空气介质来说,影响声波传播速度的主要因素为温度,Colwell等在实验室条件下测量了不同距离的声速,发现声速随温度变化的关系式均遵循[12]
(8)
式中T0=273.15 K,u0=331.45 m/s,为温度t=0 ℃时的声速.
2 空气中不同温度下声速的测量
2.1 声波的产生及频率的测量
声波的产生借助智能手机APP来实现,其中的Impulse软件较为好用,其界面易操作,可以设置起止频率及频率持续时间,在设定时间内发出随时间均匀变化的声音信号. 本文中频率的测量采用Spectral Pro Analyzer软件,其优点是可以直观的看到频率变化的曲线特征,同时直接用颜色区分不同的声强,频率间隔、更新速度等参量可以进行简单设置.
2.2 温度条件的形成
实验中选取一段薄不锈钢钢管,在外表面均匀地缠绕温控电加热带. 设定温控仪为指定温度,电热带发热之后,将热量传递到管中,待稳定平衡后,将温度传感器的探头伸入到管中心部,这样就可以对管中的温度实现控制. 由于采用的是开口管,管两端与外界存在一定热交换,这使得管两端的温度低于中心的温度. 选取20~60 ℃这个温度范围,沿着管长测量管中不同区域的温度,所得结果如图3所示.
从图3可以看出,在室温(20 ℃)条件下,管中温度沿着管长变化很小,随着温度值的升高,管中部区域温度几乎没什么变化,而管的两端由于温度升高与外界热交换更加剧烈,导致实际温度值降低.管长L=40 cm,中部10~30 cm区域能保持恒温条件.
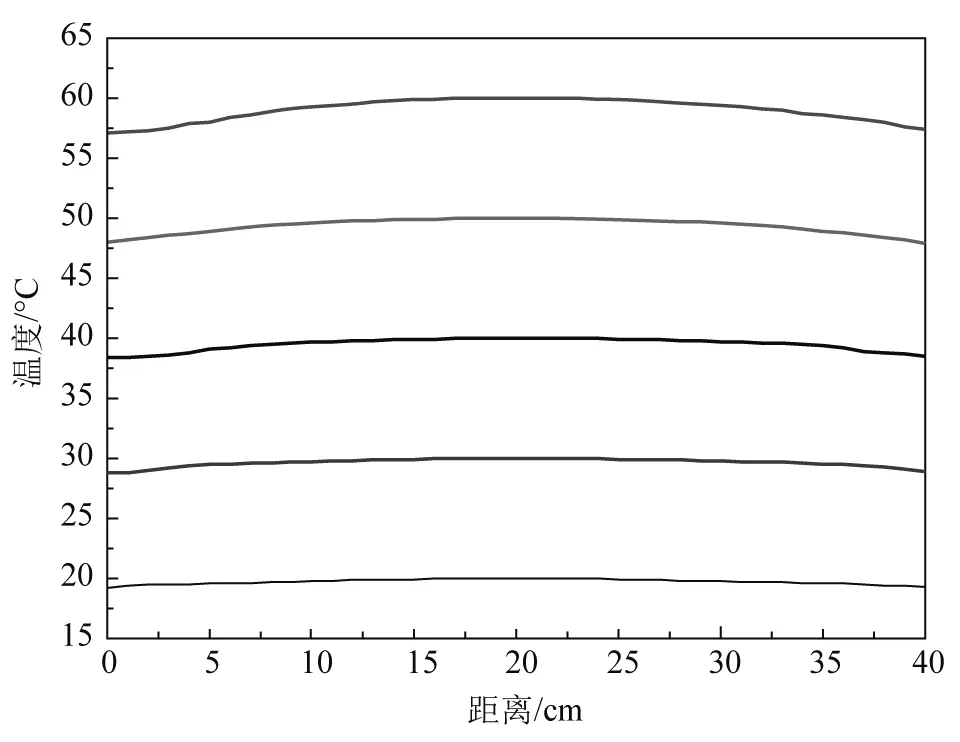
图3 管中不同位置的温度变化
2.3 测量结果及分析
实验装置如图4所示,采用两部手机,一部作为声音发射器,另一部接收频率,利用手机支架将两部智能手机固定在两侧,将直管水平固定在桌面上,使其在竖直方向上高度可调,将温度探头伸入到管的内部中心位置,进行温度的测量.

图4 实验装置图
接通温控仪和电加热带的开关,设定温控仪的控制温度,待温度稳定后,记录此时温度读数.实验时,一部手机发出的声波传播到管的另一端,被另一部手机接收,在其屏幕上显示出声音信号的频谱,手机停止发出声波后,将整个过程的频率图像截屏保存.改变温控仪的设定温度,待温度稳定以后,重复上述步骤,即可以得到不同温度所对应的波谱图.
在Impluse软件中设置起止频率为300~3 500 Hz, 持续时间为10 s. 对比没有管时直接测量的声音信号波谱图[见图5(a)]和放置管时的波谱图[见图5(b)],可以看到在图5(a)中有两条线,任意时刻有很接近的两个频率值,这可理解为手机内置传感器采集声音的振动信号时,外部声音信号也会同时引发主板的周期性振动,内置传感器感知到这些振动[13],转换为电信号,再由软件预置算法显示出对应的频率,因此有两个很接近的振动频率. 当声音通过管中传播时,图5(b)中可看到这两条线周期性的相交,由于波谱图反映的是声音频率的变化,这时不能简单将之与驻波的波形图相对应,出现这种周期性的变化可理解为在频率满足一定条件时,管中声波形成驻波,管口处为速度波腹,声压波节,这时手机传感器受到空气扰动的速度发生改变,频率也相应发生变化. 因此,测量图5(b)中交点处的频率值,可对应式(6)中的频率结果.
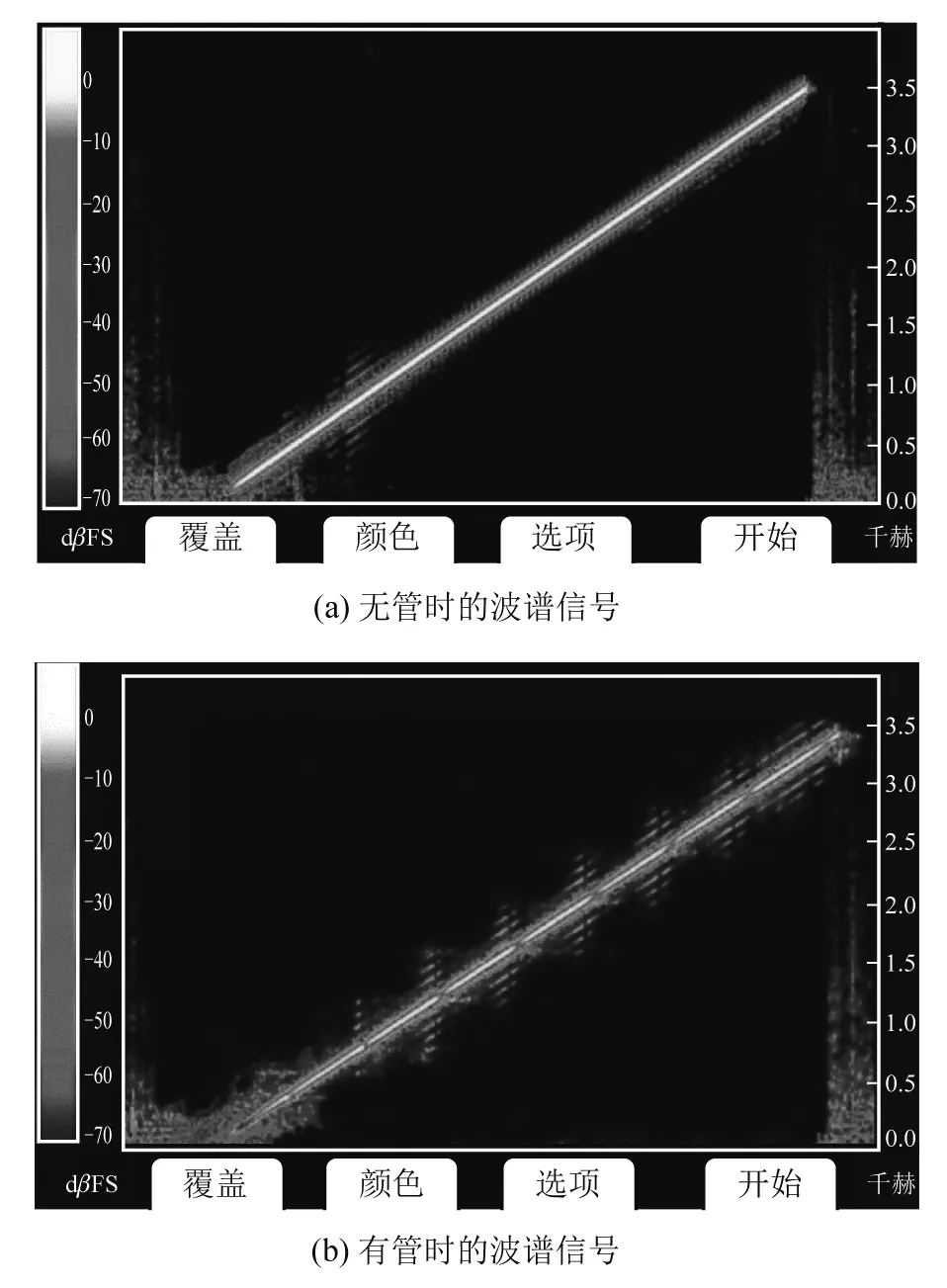
图5 波谱图(t=20 ℃)
为了精确读取频率数值,借助Gsview程序,利用比例尺原理读取出相应数据,并用逐差法计算相邻频率差的平均值,从而利用式(7)计算得不同温度下的声速实验值,数据如表1所示.将表1中的实验值和利用式(8)计算得到的理论值进行比较,可得到不同温度下的相对误差,如表2所示. 为了直观的比较,将表1和表2中数据反映的声速随温度变化的规律以及实验值和理论值的相对误差结果做图,如图6所示.
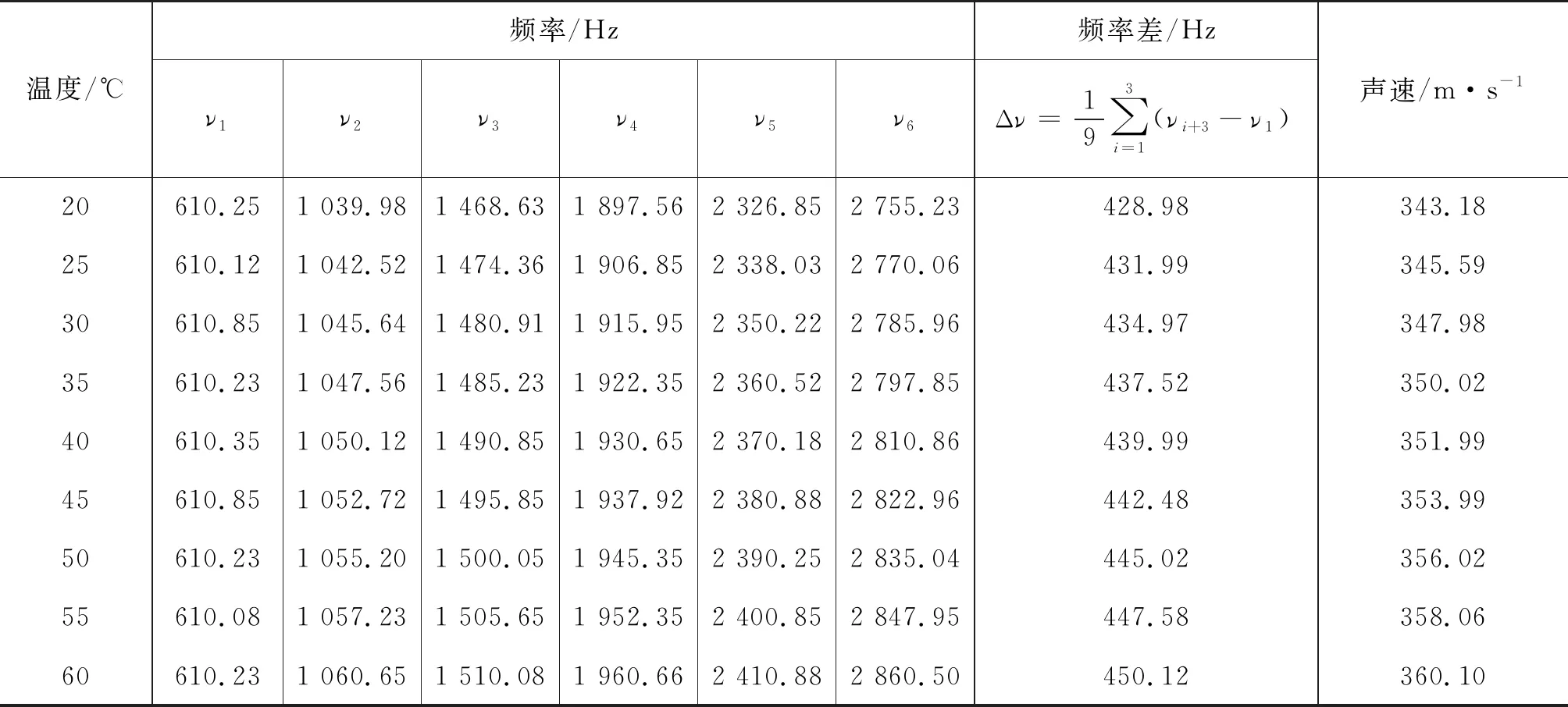
表1 不同温度下的声速
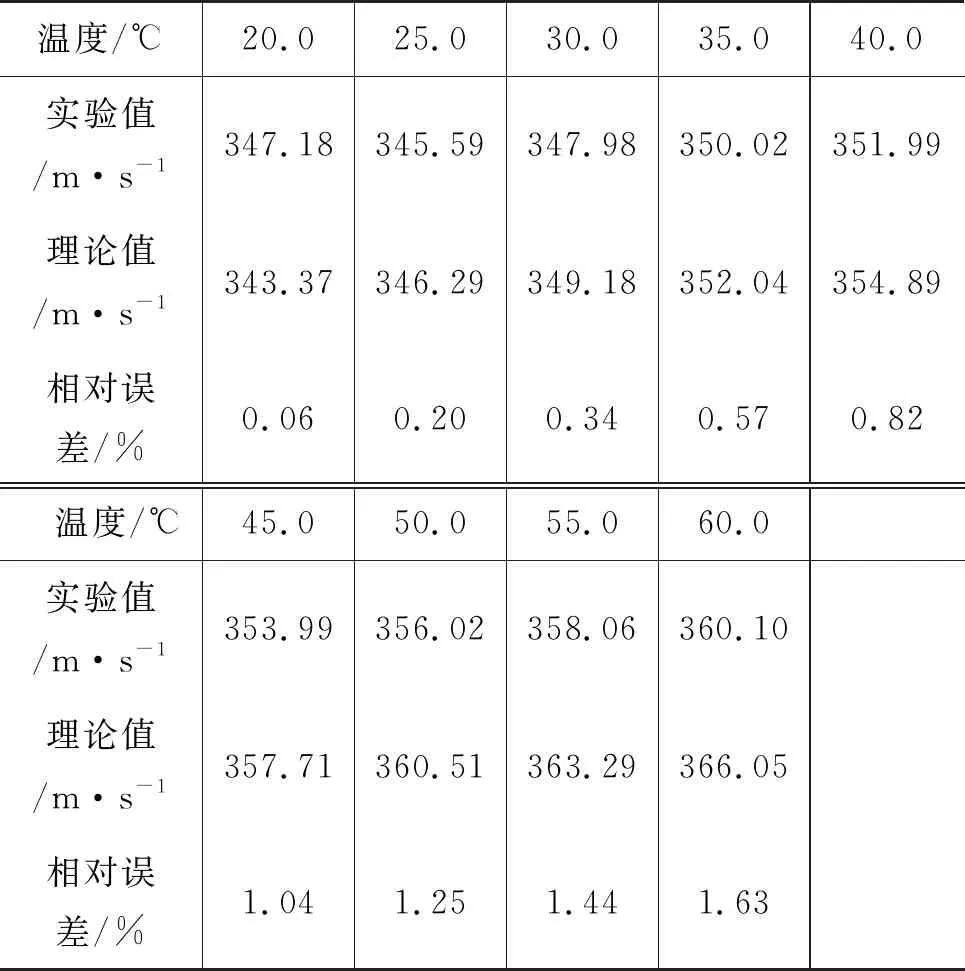
表2 不同温度下测量值的相对误差
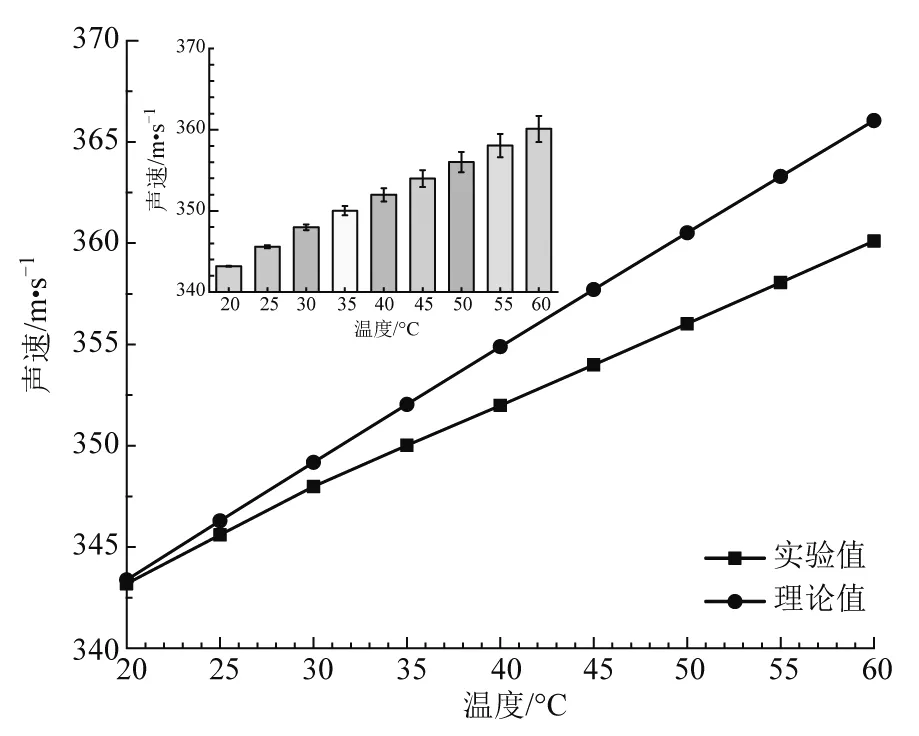
图6 声速随温度的变化及误差
从图6可以看出,声速的实验值比理论值偏小,随着温度的升高,实验值和理论值的差别越来越大,在测量范围内,所有相对误差不超过2%,其中温度40 ℃以下相对误差在1%以内,超过40 ℃则相对误差大于1%. 这是因为当温度越高时,管内温度与外界环境温差过大,热交换越发明显,管口处实际温度较理论温度值低,因而计算结果偏低.
本实验影响结果精确度的因素主要有两点:一是管口处温度与实际温度值相比较低,温度越高,偏低的数值越大,在60 ℃时可达到5 ℃,这对温度较高时测量结果的相对误差影响较大;二是波谱图的读数,测量环境越是安静,背景噪音越小,所得波谱图效果越明显,利用GSview读数越准确. 此外,本实验忽略了管口长度的校正、热胀冷缩导致的管的微小形变等因素产生的影响,在以后的实验设计中可进一步改进,但从实验结果上来看,随着温度的上升,空气中的声速不断增大,两者呈线性关系,这与声波传播速度理论相一致,且理论值和实验值的相对误差控制在2%以内,本实验方案具有一定的可行性.
3 结论
综上所述,本文根据管道中驻波的形成原理来测量不同温度条件下空气中的声速,测量结果较为准确,相对误差不超过2%,实验结果表明利用智能手机软件可实现声速的准确测量. 这种方法不仅有利于对生活中声学知识的理论学习,还可以解决离开实验室环境难以测量声速的问题,是对传统物理实验方法的改进. 本实验方案的设计基于生活中的实验器材,并不以精确测量为主要目的,更侧重于学习者对理论知识的掌握、实践动手技能和数据处理能力的初步训练,这对于提升学习者的理论知识学习能力和实验素养具有很大的益处.
