基于三次B样条小波变换和Franklin矩亚像素级图像边缘检测算法

李锦鹏，熊显名，曾启林，胡怡威，丁子婷

〈图像处理与仿真〉

基于三次B样条小波变换和Franklin矩亚像素级图像边缘检测算法

李锦鹏1,2，熊显名1,2，曾启林1,2，胡怡威1，丁子婷1

（1. 桂林电子科技大学电子工程与自动化学院，广西 桂林 541004；2. 广西高校光电信息处理重点实验室，广西 桂林 541004）

为了满足精密测量和红外与可见光图像配准对图像边缘定位的高精确度和高抗噪性的要求，提出一种基于三次B样条小波变换和Franklin矩结合的亚像素级图像边缘检测算法。首先，利用三次B样条小波窗函数对图像边缘多层分解，根据小波模极大值原理对各层检测得到初始边缘信息，随后将其边缘点与多尺度范围下3×3邻域内的点进行比较，将模值和幅角相近的点保留，建立新的边缘图像。然后，建立亚像素边缘模型，根据Franklin矩旋转不变性原理，分析图像边缘旋转至一定角度之后各级Franklin矩之间的关系，得到计算亚像素边缘点的模板关键参数，将模板在小波变换得到的新边缘图像上移动并与其覆盖下的子图进行卷积运算，进而得到图像的亚像素级边缘点。实验结果表明，并与当下表现较优的3种算法进行对比，本文提出的基于三次B样条小波变换和Franklin矩结合的算法精确度更高且抗噪性更强，能够更好地满足对于红外与可见光图像配准稳定可靠及高精度测量的要求。

边缘检测；三次B样条小波；Franklin矩；亚像素；图像配准

0 引言

边缘是一幅图像的基本特征，同时边缘检测也是图像分析和测量技术[1]的基本问题，尤其在红外图像配准以及视觉测量等领域中[2]对图像边缘检测技术的要求极高。边缘检测其实就是利用算法对图像突变信息的检索。传统的边缘检测算子有Sobel算子、Krisch算子、Roberts算子以及Canny算子，这些微分算子相对比较简单，对于复杂环境下的图像边缘把握不足，精度较差，缺乏细节。随着人民生活水平的提高和科学技术的不断发展，普通像素级别也已经无法满足机器视觉和精密测量上的需求，因此，亚像素技术在这方面显得非常重要，目前常用的亚像素边缘检测方法有：插值法，矩方法，拟合法等，其中矩方法在复杂环境下表现良好，对噪声不敏感，是一种在目前有效的亚像素图像边缘检测方法。

1993年Ghosal等[3]最早提出利用正交矩对图像边缘进行亚像素级检测的算法，首次通过计算3个不同阶次的Zernike正交矩，然后将理想状态下的灰度模型参数映射到3个Zernike正交矩上，计算得到边缘所在的直线参数，进而确定亚像素坐标。但是该算法比较局限，因为不同模板选择，坐标的计算也会产生误差，而且理想阶跃模型与实际存在差异。针对这个问题，李金泉等[4]提出了一种改进的Zernike正交矩检测算法，采用边缘梯度方向一阶导数模型的同时考虑了模板放大效应，提高了亚像素边缘检测的准确度。高世一等[5]在考虑模板放大效应的情况下，提出了新的边缘定位条件。吴一全等[6]人用了更大的模板，但是对噪声变得敏感，抗噪性较差。为此，魏本征等[7]提出了形态学梯度算子和Zernike矩相结合，使检测变得更稳定，抗噪性变强，但是对于微小的细节检测较弱。吴一全等[8]基于Franklin矩提出了一种新的边缘检测算法，但是对于边缘微小的细节把握稍显欠缺。Franklin矩所基于的Franklin函数仅有一次分段多项式组成，而且避免了复杂的高次多项式计算，在具有Zernike矩的大部分优点的同时，还具有复杂度低，数据稳定等优点，使得边缘检测得到的信息具有独立性，没有冗余。因此，本文将三次B样条小波变换和Franklin矩结合起来，提出一种多尺度取模极大值的亚像素检测算法，该方法结合小波变换的模极大值原理使得边缘细节的提取更准确，然后用改进后的Franklin矩算子对得到的图像进行亚像素边缘提取。并与基于Zernike矩的算法、基于Franklin矩的算法、基于Roberts算子和Zernike矩结合的算法进行比较。

1 三次B样条小波模极大值边缘检测原理

三次B样条小波模极大值其实就是利用三次B样条小波函数与得到的信号进行卷积运算，然后将计算结果取它的模值，最后找到里边的模极大值。在图像的处理中，小波变换的模极大值代表着包含图像信息最丰富的点，利用这个特征我们可以通过计算小波模极大值来提取准确的图像边缘信息。同时，文献[9]提出三次B样条小波的时域局部特性较接近于Gauss函数，且它的紧支集性质相比Gauss函数更好。而且，因为B样条函数是对称的，所以保证了对应相位的线性性质，避免了后期相位失真情况的出现。

式中：和积分均满足为0的条件，同时可以将它们看成两个二维小波函数。通常情况，(,)取为二维高斯函数，其表达式以及一阶偏导数的表达式为：

式中：为正态分布标准偏差。

而对于(,)Î2()任意的图像，在尺度为时的小波变换在和方向上的两个分量分别为：

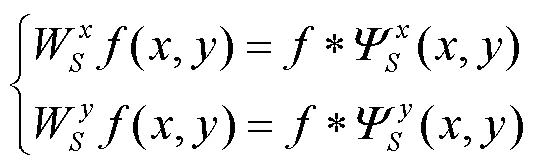
则小波变换在其尺度为的条件下，梯度上的模以及幅角分别为：

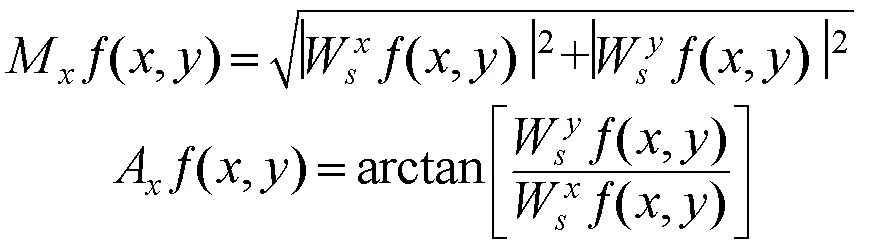
式中：(,)是二维信号；2()是函数域。

梯度模值Mf(,)对应的是目标图像在点(,)处的灰度变化情况，梯度幅角Af(,)对应的是梯度向量和水平方向的夹角。目标图像上的边缘特征点即为在梯度方向上模为其局部极大值的点。

2 基于Franklin矩的图像亚像素边缘检测

2.1 Franklin函数及其Franklin矩

Franklin函数是由Philip Franklin提出的定义在2[0,1]上的连续正交函数系[10]，它是由一组线性无关的截断幂基在正交化之后得到的。首先，考虑以下的线性无关组{(),0≤≤1}：

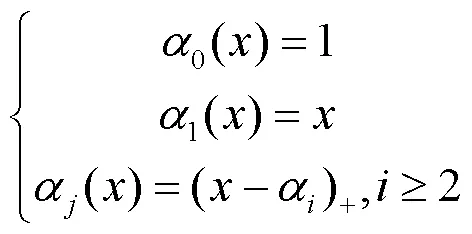
0()＝1, 0≤≤1 (6)

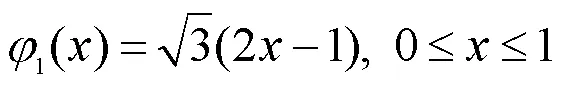
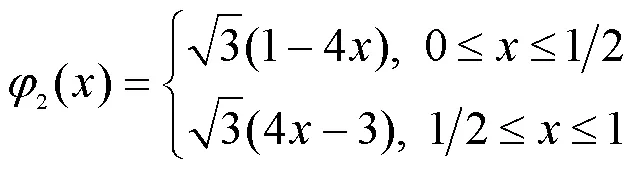
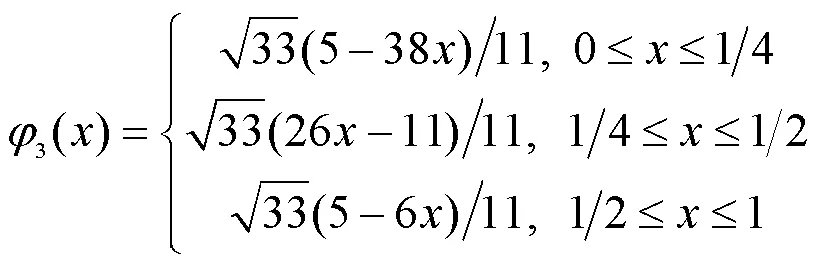
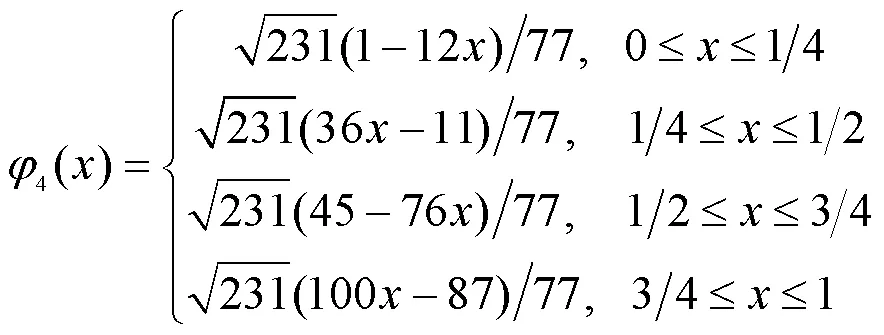
Franklin矩是由上述Franklin函数所定义的，假设第个Franklin函数记为：()，0≤≤1，≥0，而目标图像函数记为(,)，0≤，≤1，则它的第阶次Franklin矩为：

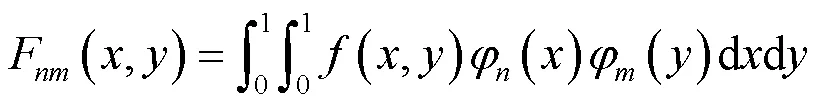
为了在极坐标中更直观地看到其Franklin矩所具有的正交性和旋转不变性，这里将目标图像函数记为(,)，则在极坐标系(,)下，图像的阶次Franklin矩为：

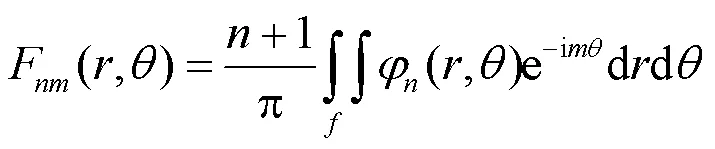
矩是对目标图像特征的定量描述，正是因为Franklin矩有着独特的正交特性，使得目标图像的每个Franklin矩都是互不干扰的，这就能将图像进行最大程度的分解，从而采用较少的Franklin矩描述图像得到更多的特征信息，以便达到降低特征维数，降低计算复杂度的目的。

2.2 基于Franklin矩的亚像素检测算法

由上述Franklin矩的极坐标定义式(12)以及它的旋转不变性可知若目标图像旋转角，则旋转之前的Franklin矩F和旋转角之后的Franklin矩¢之间的关系为：

F＝¢e－im(13)

由上述式(13)能够发现目标图像在旋转一定角度之后只是相位发生了变化而已，它的Franklin矩模值并未产生任何改变。基于Franklin矩的边缘检测算法是通过建立Franklin矩和理想亚像素模型的4个边缘参数的关系，然后再分别求解Franklin矩得到目标图像的4个边缘参数，设定合适的阈值将其进行筛选，得到精确的亚像素图像边缘点。平面亚像素边缘检测模型如图1所示。其中为理想边缘，单位圆被其分成两个区域，为图像背景灰度，为圆心到边缘的垂直距离，为边缘两侧的灰度差即阶跃高度，和对应在不同阶次Franklin矩的两条边缘，1和2分别是圆心到其两条阶跃边缘的距离，图1(a)顺时针旋转角得图1(b)。

Franklin矩的复数域阶多项式定义为：

V(,)＝R()eim(14)

式中：和为整数，且为－||非负的偶数。

由Franklin矩原理，定义为圆心到(,)的矢量长度，i为虚数单位，则径向多项式R为：

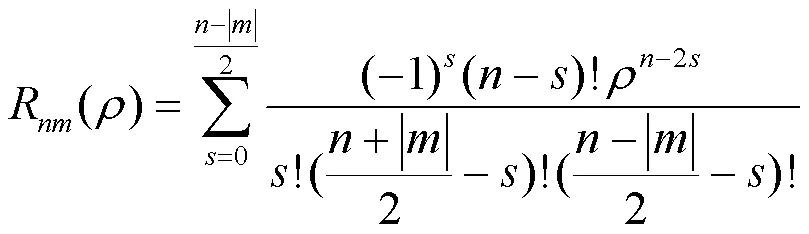
由式(15)得到部分径向多项式R值如表1所示，为圆心到点(,)的距离。

根据式(14)和表1计算出Franklin矩的复数域多项式，如表2所示。

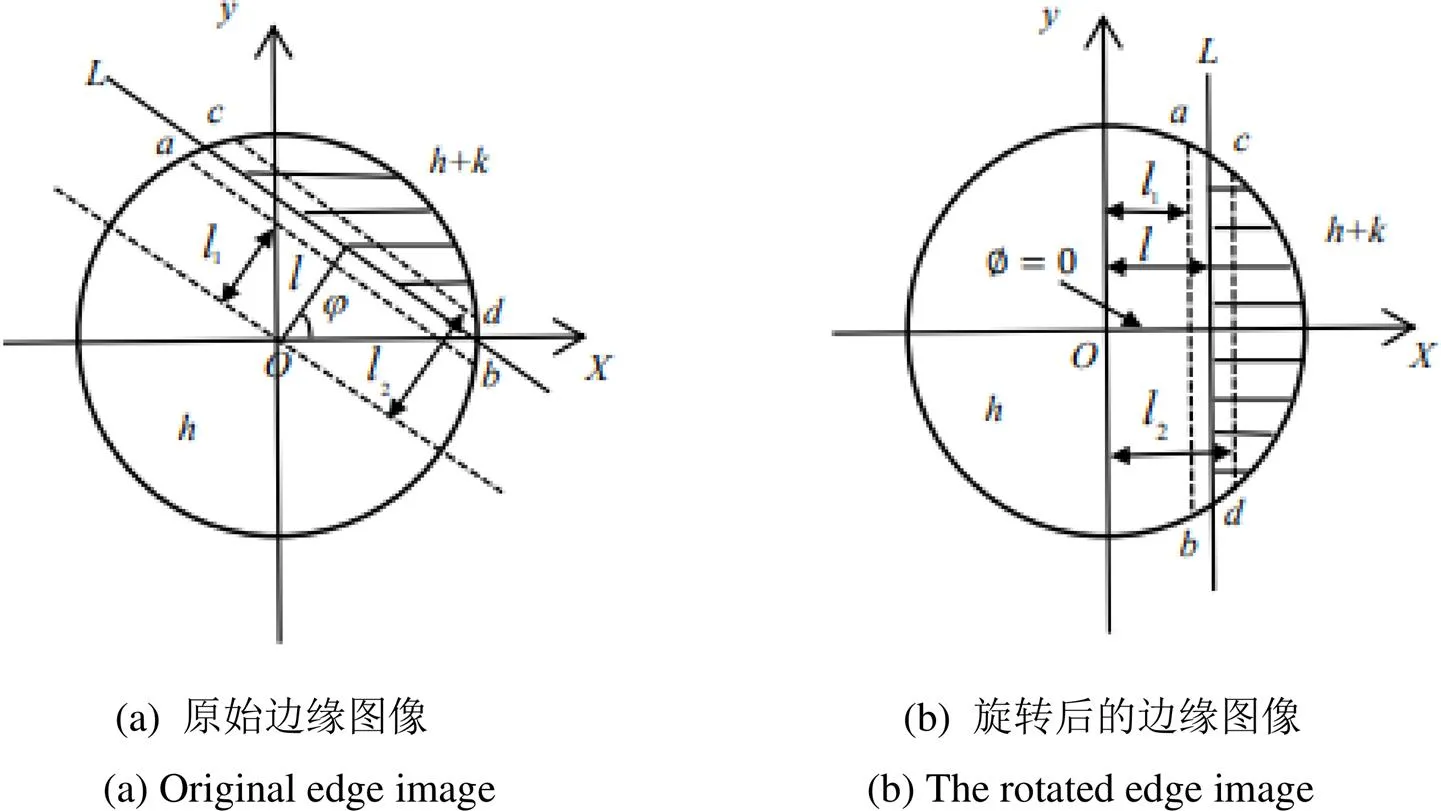
图1 亚像素边缘检测模型

表1 Franklin径向多项式Rnm

表2 Franklin矩的复数域多项式Vnm

在单位圆内，由Franklin矩定义和图1(b)中的边缘阶跃模型可得：

解20¢和40¢的方程可得：

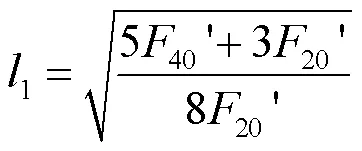
解11¢和31¢的方程可得：

根据式(13)可得：

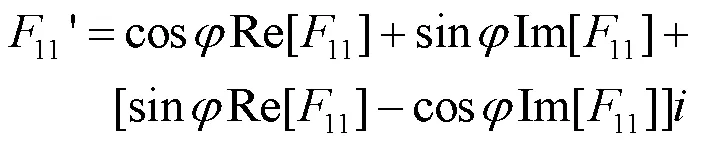
根据图1可以看出，Im[11¢]是关于轴的奇函数，所以：

微信的商业价值不言而喻。以“江小白”为人物原型的微信表情包被多次下载转发，其研发的“小白快跑”，“小白2048”，“摇骰子”，“真心话大冒险”等微信小游戏，借助时下最火的小游戏，融入江小白的元素，打造江小白专属，使酒前饭后人们的娱乐活动都深深打上江小白的烙印，拉近了与潜在消费者的距离，实现了良性互动。

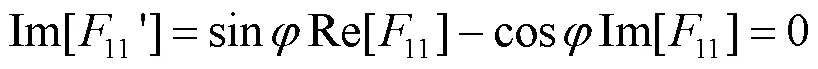
则：

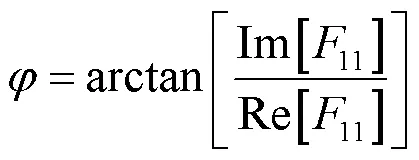
确定亚像素边缘阶跃模型的参数之后，可得Franklin矩亚像素图像边缘检测式[11]为：

式中：(s,s)为亚像素点坐标；(,)为圆心坐标。设定Franklin矩模板为×，则式(23)换算为：

模板选择过小会导致边缘提取的信息不全，过大会对噪声过于敏感，本文采用Franklin矩模板为7×7。

3 边缘检测判定和检测算法步骤

在对目标图像的具体分析时，如果整幅图像边缘提取的话，尺度就会容易过大，图像就会变得平滑，细节就会缺失[12]，利用小波窗函数原理高频之处时间细分，低频之处频率细分，能够在抑制噪声信号的前提下，得到良好的图像边缘检测效果。三次B样条小波满足本文算法对于小波基函数的3个基本条件：①高通滤波器②检测边缘的小波为奇函数③紧支窗口函数。本文基于三次B样条小波和Franklin矩的亚像素边缘检测算法步骤如下所述：

1）利用三次B样条小波函数[13]对目标图像进行多层分解，本文算法选取的层数＝3。

2）根据其小波模极大值原理对每一层进行单尺度边缘检测，计算出其得到的模极大值S(,)和对应的幅角A＝(,)，利用Otsu法（最大类间方差法）自适应确定阈值t，将所有模值进行筛选，当S(,)＞t时，E(,)即可得到目标图像的边缘信息。

4）计算Franklin矩7×7模板{00,11,20,31,40}，将这个模板在边缘图像(,)上移动，并与模板上的子图卷积运算，得到{00,11,20,31,40}。

5）根据2.2节中介绍的公式计算出平面亚像素边缘阶跃模型的参数和，代入式(24)中计算得到亚像素坐标。

4 实验结果与分析

为了验证本文算法的优越性和有效性，做了大量的验证和对比，获取了大量的参考数据，由于篇幅有限，将以两部分加以说明。本文实验环境为Intel(R) Core( TM) i5-8250U、8G RAM、MATLAB R2016b。

由于在实际应用中图像都会受到不同程度噪声的干扰，那么确定合适的阈值就显得尤为重要，不同的区域阈值会大不相同，有可能在某一区域效果良好的阈值在另一区域的效果会相对较差，本文采用一种自适应阈值方法（Otsu法）进行处理，实验效果图如图2所示。

图2 自适应阈值化图像

将自适应阈值化后的图像与模值进行对比，得到筛选后的图像边缘信息，并有效地去除噪声，并在合适尺度下进行局部对比，提取模值和幅角相近的信息，剔除部分伪边缘点，最后套入计算好的Franklin矩模板进行卷积运算，得到点坐标。

第一部分实验的目的是为了验证本算法对目标图像的边缘提取达到亚像素级别，制作一幅128×128的二值图像，在图像中插入一个半径为50的圆，圆心坐标为(64,64)，如图3(a)所示，为了验证抗噪性，在制作的二值图中加入高斯噪声，如图3(b)所示。

提取图3(b)圆上任意10个点的坐标，并用本文算法得到这10个点的亚像素坐标，计算它们的误差，表3所示。

从表3中可以看出，采用本文算法检测边缘点坐标最大误差为0.1497，能将误差控制在很小的范围内并且整体误差偏小，亚像素边缘定位精度较高。为了更进一步地验证本文算法的优越性，将在第二组实验中与基于Zernike矩的算法、基于Franklin矩的算法、基于Roberts算子和Zernike矩结合的算法进行比较。

图3 二值图像

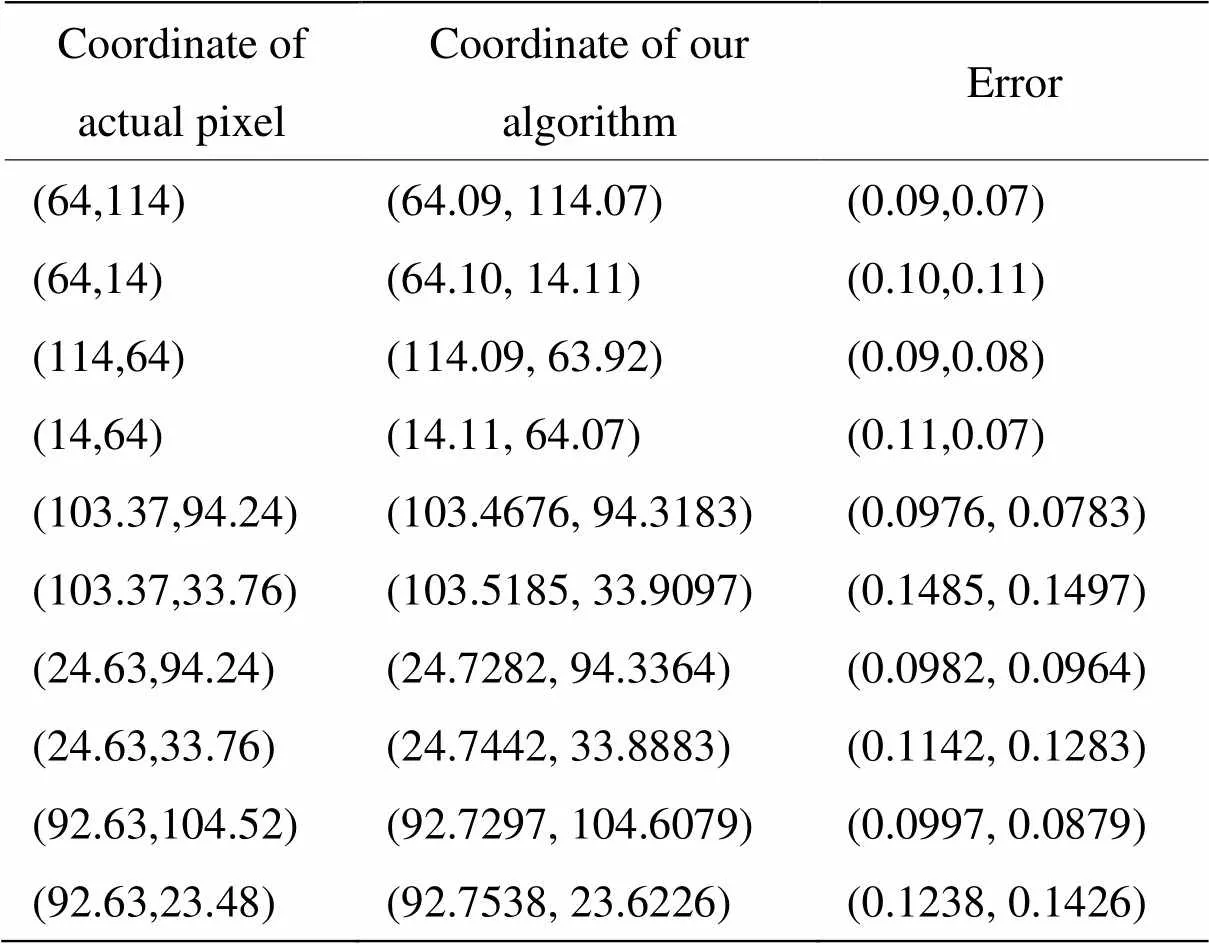
表3 检测的亚像素坐标

第二组实验中选用具有丰富纹理的Lena图像，并且为了验证鲁棒性，本文将对Lena图像加入高斯噪声，相应的结果和对比如图4(c)～(f)所示。通过对比我们可以发现，Zernike矩算法能够较好地抑制高斯噪声，但是在抑制噪声的同时也将目标图像的边缘弱化了，导致边缘信息极大缺失；Franklin矩算法在很好地抑制高斯噪声的同时能较好地提取边缘，但也存在部分细节缺失；Roberts算子＋Zernike矩结合算法在Zernike矩算法的基础上试图加入Roberts算子以增强边缘定位，但Roberts算子有着对噪声信号极其敏感的特性，所以可以看到在边缘信息得到补充的同时也带来了噪声的影响，抗噪性较差；本文基于三次B样条小波＋Franklin矩结合算法能够在抑制噪声的同时，很好保留图像边缘信息，并且定位更加准确，通过标记的小方框部分对比，可以发现本算法得到的边缘信息更加完整，细节方面对比其他3种算法也更丰富。

为了更有效地验证本文算法的实时性和抗噪性，对图4中4种不同算法的运行时间和峰值信噪比进行比较，结果分别如表4和表5所示。实验结果表明，本文算法在具有更复杂的计算流程情况下，运行时间仍与Zernike矩和Franklin矩两种算法相当，并且大幅短于Roberts算子＋Zernike矩结合算法，实时性较强，在抗噪性方面，本文算法明显大幅优于其他3种算法，结果表明，在运行时间相当的情况下，本文算法有着更优的效果，更具实用性。

图4 Lena 图像及4种算法的边缘检测结果

表4 四种算法运行时间

表5 四种算法峰值信噪比

5 结论

本文提出了一种基于三次B样条小波变换和Franklin矩相结合的亚像素级图像边缘检测算法。利用三次B样条小波对图像进行粗处理，在得到预边缘后再利用Franklin矩的特性计算出亚像素边缘点的模板关键参数，将模板在小波变换得到的新边缘图像上移动并与其覆盖下的子图进行卷积运算，进而得到图像的亚像素级边缘。实验结果表明，与基于Zernike矩的算法、基于Franklin矩的算法、基于Roberts算子和Zernike矩结合的算法相比，本文提出的算法具有更高的检测精度和更强的抗噪性，并且通过实际坐标和得到的边缘亚像素点坐标对比可知，本文的算法误差较小，图像边缘点定位可靠，在红外与可见光图像配准和精密测量上具有良好的应用前景。

[1] 金光远. 图像测量技术与系统[D]. 长春: 吉林大学, 2008.

JIN G Y. The Design and Realization for the Measuring System Based on Image Processing[D]. Changchun: Jilin University, 2008.

[2] 戴宪策, 刘昌锦. 快速亚像素图像配准算法研究[J]. 红外技术, 2015, 37(7): 579-581.

DAI Xiance, LIU Changjin. Research on fast sub-pixel image registration algorithm[J]., 2015, 37(7): 579-581.

[3] Ghosal S, Mehrotra R. Orthogonal moment operators for subpixel edge detection[J]., 1993, 26(2): 295-306.

[4] 李金泉, 王建伟, 陈善本, 等. 一种改进的Zernike正交矩亚像素边缘检测算法[J]. 光学技术, 2003, 29(4): 500-503.

LI J Q, WANG J W, CHEN SH B, et al. An improved Zernike orthogonal moment sub-pixel edge detection algorithm[J]., 2003, 29(4): 500-503.

[5] 高世一, 赵明扬, 张雷, 等. 基于Zernike正交矩的图像亚像素边缘检测算法改进[J]. 自动化学报, 2008, 34(9) : 1163-1168．

GAO S Y, ZHAO M Y, ZHANG L, et al. Improvement of image sub-pixel edge detection algorithm based on Zernike orthogonal moments[J]., 2008, 34(9): 1163-1168．

[6] 吴一全, 龙云淋, 周杨. 基于Arimoto熵和Zernike矩的刀具图像亚像素边缘检测[J]. 华南理工大学学报: 自然科学版, 2017, 45(12): 50-56．

WU Y Q, LONG Y L, ZHOU Y. Sub-pixel edge detection of tool image based on Arimoto entropy and Zernike moment[J].: Natural Science Edition, 2017, 45(12): 50-56．

[7] 魏本征, 赵志敏, 华晋. 基于改进形态学梯度和Zernike矩的亚像素边缘检测算法[J]. 仪器仪表学报, 2010, 31(4): 838-844．

WEI B Z, ZHAO Z M, HUA J. Sub-pixel edge detection algorithm based on improved morphological gradient and Zernike moment[J]., 2010, 31(4): 838-844.

[8] 吴一全, 邹宇, 刘忠林. 基于Franklin矩的亚像素级图像边缘检测算法[J]. 仪器仪表学报, 2019, 29(5): 221-229.

WU Y Q, ZOU Y, LIU Z l. Sub-pixel image edge detection algorithm based on Franklin moment[J]., 2019, 29(5): 221-229.

[9] 杨小娜, 黄欢, 徐晓煜, 等. 基于小波模极大值多尺度的图像边缘提取[J]. 贵州大学学报: 自然版, 2013, 30(1): 91-93.

YANG X N, HUANG H, XU X Y, et al. Multi scale image edge extraction based on wavelet modulus maxima[J].: Natrual Edition, 2013, 30(1): 91-93.

[10] Franklin P. A set of continuous orthogonal functions[J]., 1928, 100(1): 522-529.

[11] DA F, ZHANG H. Sub-pixel edge detection based on an improved moment[J]., 2010, 28(12): 1645-1658．

[12] 朱文斌, 雷秉山, 雷志勇. 基于小波变换的红外探测系统信号去噪[J]. 红外技术, 2018, 40(11): 1047-1051.

ZHU W B, LEI B S, LEI ZY. Signal denoising of infrared detection system based on wavelet transform[J]., 2018, 40(11): 1047-1051.

[13] 刘小豫, 韩丽娜, 赵蔷. 基于B样条小波的图像边缘检测算法[J]. 电子设计工程, 2013, 21(14): 178-180.

LIU X Y, HAN L, ZHAO Q. Image edge detection algorithm based on B -spline wavelet[J]., 2013, 21(14): 178-180.

Sub-pixel Level Image Edge Detection Algorithm Based on Cubic B-spline Wavelet Transform and Franklin Moment

LI Jinpeng1,2，XIONG Xianming1,2，ZENG Qilin1,2，HU Yiwei1，DING Ziting1

(1.,,541004,;2.,541004,)

To meet the requirements of high accuracy and strong anti-noise performance of image edge positioning for infrared and visible image registration and precision measurement, a sub-pixel image edge detection algorithm based on the cubic B-spline wavelet transform and Franklin moment is proposed. First, the image edge was decomposed using a cubic B-spline wavelet window function. Under the premise of setting the threshold, according to the principle of wavelet modulus maxima, the initial edge information is detected for each layer, and then the edge points are compared with the points in the 3 × 3 neighborhood in the multi-scale range. Points with similar moduli and amplitudes were reserved to establish a new edge image. Subsequently, a subpixel edge model is established. According to the principle of Franklin moment rotation invariance, the relationship between Franklin moments at all levels after the image edge is rotated to a certain angle is analyzed and the key parameters of the template for calculating the sub-pixel edge points are obtained. The template is moved on the new edge image obtained by wavelet transform and convoluted with the sub-image covered by it, and then the sub-image of the image is obtained from the edge points of the prime level. The experimental results show that, compared with the three algorithms with the current best performance, the algorithm based on the combination of the cubic B-spline wavelet transform and Franklin moments proposed in this paper has higher accuracy and stronger noise resistance. It can better meet the requirements for stable, reliable, and high-precision measurements of infrared and visible image registration.

edge detection, cubic B-spline wavelet, Franklin moment, sub-pixel, image registration

TP391.4

A

1001-8891(2022)03-0255-07

2020-07-05；

2020-08-19.

李锦鹏（1995-），男，硕士研究生，主要研究方向为机器视觉。E-mail：503482546@qq.com。

熊显名（1964-），男，研究员，主要研究方向为光电测量，机器视觉。E-mail：XXM5864@163.com。

国家科技重大专项课题（2017ZX02101007-003）。