带截体聚能装药正交优化设计

王瑞琪，孙 焕,2，任鑫鑫，吴家祥，黄骏逸，武双章，李裕春

(1.陆军工程大学野战工程学院，南京 210007；2.中国人民解放军31671部队，辽宁 辽阳 111000)

1 引言

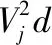
2 几何模型及正交设计

带截体聚能装药主要由高能炸药，外壳，药型罩及截体等结构组成。带截体聚能装药结构如图1所示：药型罩口径=50 mm，截体底径50 mm，截体顶角60°，截体顶直径5 mm，壳体厚度1.5 mm。

图1 带截体聚能装药几何模型示意图Fig.1 Geometric model of shaped charge with truncated body

选定罩锥角，罩壁厚，药顶高及截体间距作为正交设计的4因素，分别使用、、、表示，每个因素设置3个水平，分别用1、2、3表示，如1表示的1水平，即罩锥角取1水平。因素水平表如表1所示，各水平都在理想范围内取值。根据因素数和水平数并考虑一级交互作用，选择正交表进行试验方案设计，利用混杂有效减少试验个数，试验设计表头如表2所示。称射流穿过截体后为剩余射流，考核指标选择剩余射流断裂头部直径(简称为头部直径)和剩余射流断裂头部速度(简称为头部速度)。

表1 正交分析因素水平表Table 1 Factors and levels of orthogonal analysis

表2 试验设计表头Table 2 Design scheme of testing

3 有限元模型及材料参数

采用非线性动力学分析软件AUTODYN-2D建立二维1/2有限元模型如图2所示。模型由炸药，药型罩，外壳，截锥体和空气组成，由于炸药爆炸以及药型罩在压垮过程中材料变形大，使用Euler，2D Multi-material求解器计算；为减少网格数目并获得更好的射流形态，采用轴渐变网格的建模方式；在空气域边界建立FOLW-OUT 边界条件，目的是为了模拟无限空气域、消除边界效应；起爆方式采用装药底部端面中心点起爆方式；同时还模拟了同一结构参数无截体装药，目的是对比截体对射流成型以及运动的影响；单位制mm-mg-μs。

图2 聚能装药有限元模型图Fig.2 Finite element model

除炸药外，所有材料3使用AUTODYN内置材料库中的材料。装药壳体使用Al-2024，采用状态方程SHOCK；药型罩使用COPPER，采用状态方程SHOCK和强度模型Piecewise JC；截锥体使用NYLON，采用状态方程SHOCK；空气采用理想气体状态方程。炸药选用8701炸药，采用高能炸药JWL状态方程，参数如表3所示。

表3 8701炸药JWL状态方程参数Table 3 JWL equation of state parameters of 8701 explosives

4 计算过程及结果

数值模拟获得的典型射流形成的过程如图3所示。0时刻8701炸药起爆，爆轰波与顶外壳作用，顶外壳开始发生变形向外扩展；2.6 μs爆轰波到达药型罩锥顶，与药型罩发生剧烈碰撞，药型罩开始在爆轰波的压力作用下逐渐被压垮；7.8 μs爆轰波波阵面传到药型罩的末端位置，这时，药型罩的顶部已经被压垮，药型罩材料向中间汇聚，射流头部已经开始形成；12.4 μs时射流头部开始侵彻截锥体，并在截体内形成冲击波，射流头部由于截体的阻挡，能量和速度下降；17.3 μs时射流翼部开始撞击截体，并形成新的冲击波，加速截锥体的破坏；30.8 μs时射流穿过截体，速度下降放缓；33.3 μs时射流头部率先断裂，随后断裂为多段。如图4所示，与无截体装药形成的射流形态进行对比，带截体装药形成的射流头部平整，直径得到了大幅度提升，速度小幅度下降。

图3 典型射流形成过程示意图Fig.3 Schematic diagram of typical jet formation process

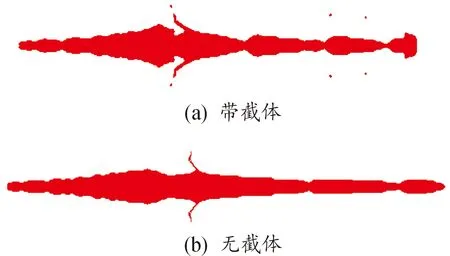
图4 射流形态图Fig.4 Comparison diagram of jet state

完成54组试验之后将数值模拟结果见表4，指标1为，指标2为。作为对比，列入了无截体装药形成射流情况，其中为无截体装药形成射流断裂头部直径；为无截体装药形成射流断裂头部速度；Δ为射流在截体作用下直径提高的百分比；Δ为射流在截体作用下速度下降的百分比。在截体作用下，头部直径平均值为5.32 mm，头部速度平均值为4 268.7 m/s。无截体作用时，头部直径平均值为2.71 mm，头部速度平均值为5 314.8 m/s。可以看出，截体作用可以使头部直径平均提高47.29%，头部速度平均下降19.66%。说明使用尼龙作为截体材料可以使剩余射流断裂头部直径大幅增加，速度小幅度下降。

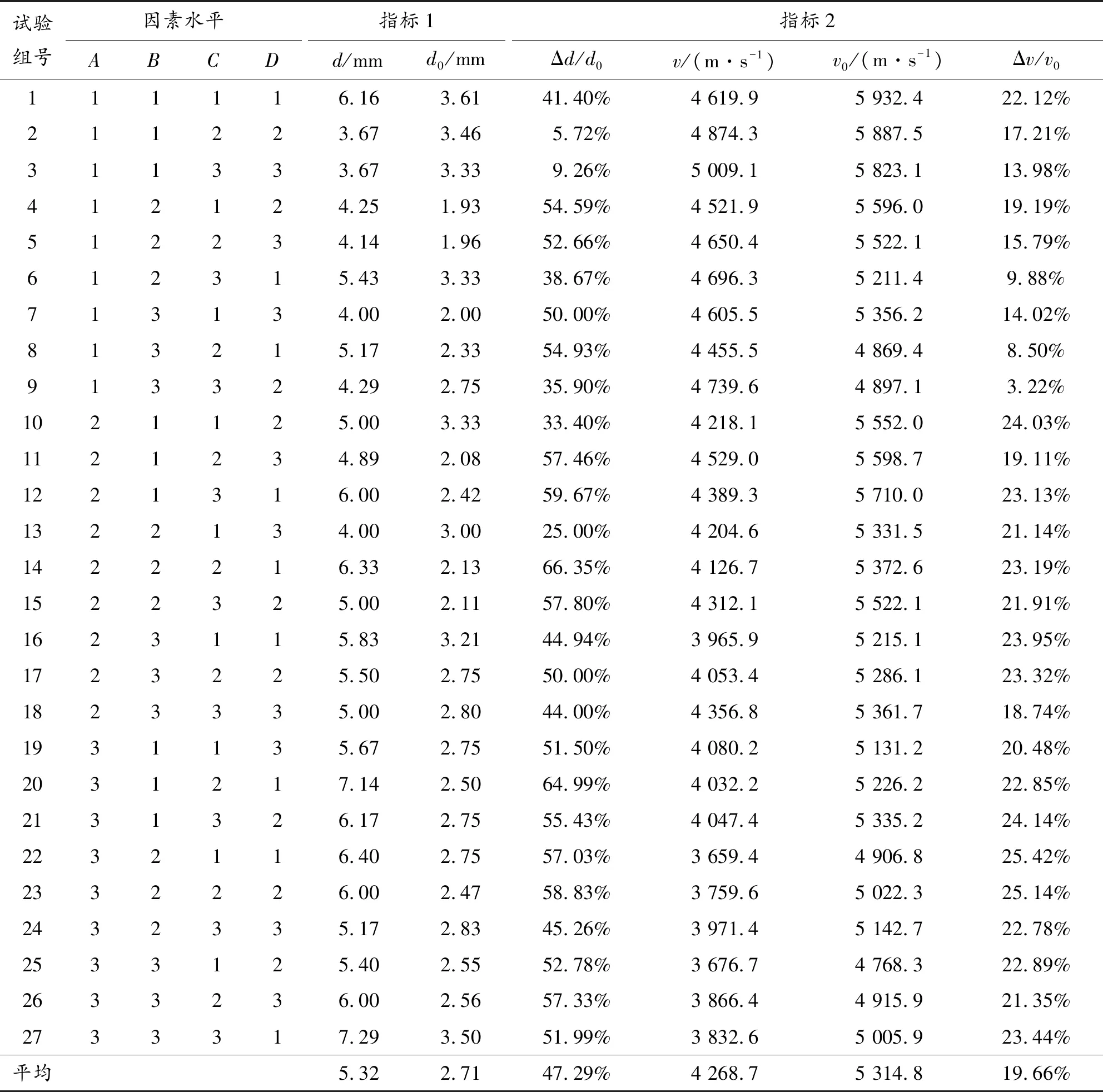
表4 数值模拟结果Table 4 Results of numerical simulation

5 数据分析及优化结果

使用极差法分析模拟试验数据，将交互列也看作一个因素，计算出各列极差值。极差值的大小反映了各因素对试验指标变化的幅度，某因素的极差越大，该因素对于考核指标的影响也就越大。

从表5中可知，对于头部直径这一考核指标，罩锥角影响最大，以3最佳；截体间距次之，以1最佳；罩锥角与药顶高交互作用×更次；罩壁厚与药顶高交互作用×再次；之后依次为××、××、。因此，各因素主次顺序为：、；×、×、××、××、。(分号代表前后因素极差相差较大，顿号代表前后因素极差相近)

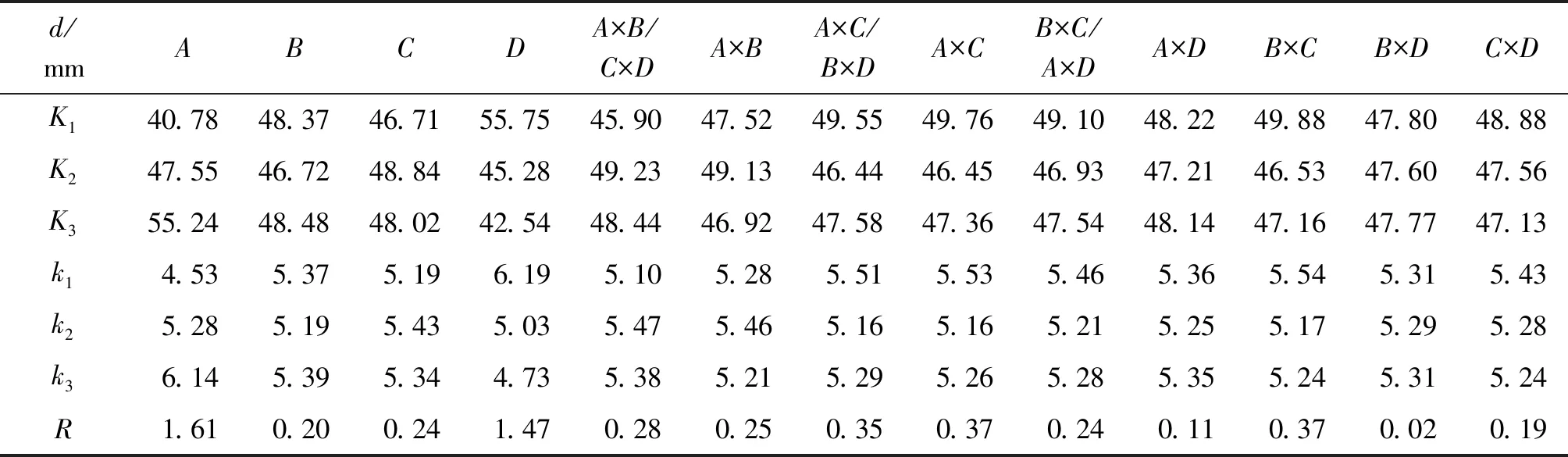
表5 极差表(头部直径为指标)Table 5 Range table (head diameter as index)

可以看出，对于头部直径这一考核指标，交互作用×、×分别位于主要因素的第三和第四位。对于交互作用×，写出其搭配表，如表6所示，可知3×2、3×3、3×1可以获得较大的直径，因此选取3×2、3×3和3×1作为×的较优搭配。对于交互作用×，写出其搭配表，可知1×1、3×2、3×3可以获得较大的直径。因此，优化结果为3111、3321、3331(27号方案)。由于3111、3321在已有27个试验中并无试验方案，对其进行建模和数值模拟，分别命名为28号和29号试验方案。由表7可以看出，28号方案和29号方案射流直径分别为6.50 mm和6.71 mm，小于27号方案的7.29 mm。因此优选27号方案3331为最优方案。

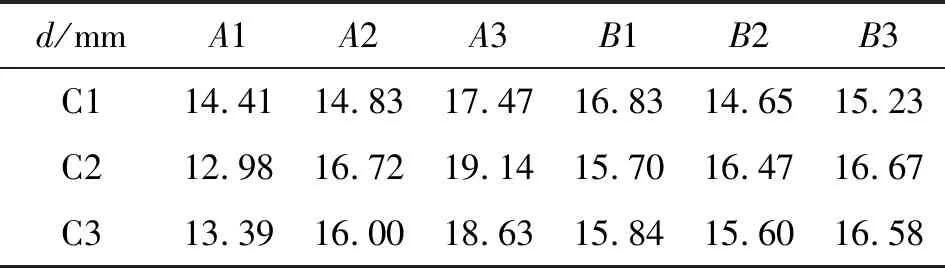
表6 A×C和B×C搭配表(头部直径为指标)Table 6 Matching table of A×C and B×C (head diameter as index)

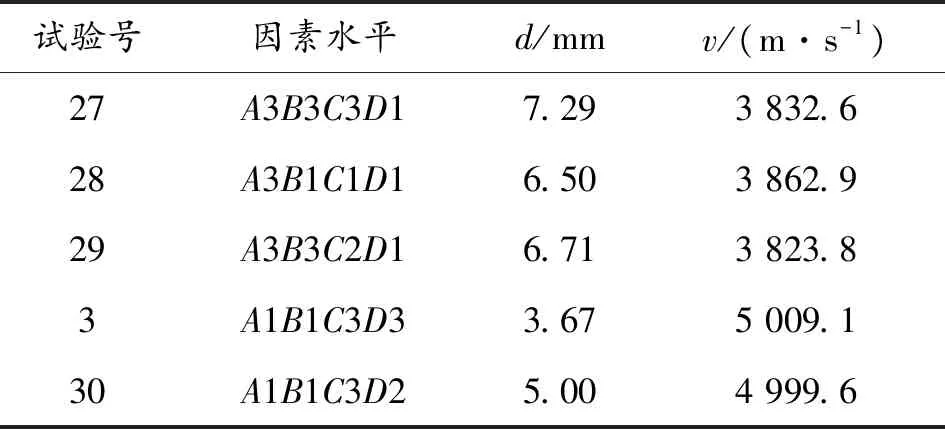
表7 优化方案对比Table 7 Comparison of optimization schemes

对于头部直径的最优结果27号方案，其对应的无截体装药形成的射流直径为3.50 mm，直径提高了51.99%，射流速度下降了23.44%。

27号方案、28号方案和29号方案射流形态见图5所示。

图5 优化方案射流形态对比Fig.5 Jet shape comparison of optimized schemes

从表8可知，对于头部速度(速度大为佳)这一考核指标，罩锥角影响最大，以1最佳；罩壁厚次之，以1最佳；药顶高更次，以3最佳；截体间距再次，以3最佳；之后依次为××、××、×。因此，各因素主次顺序为：；、、、××；××、×。

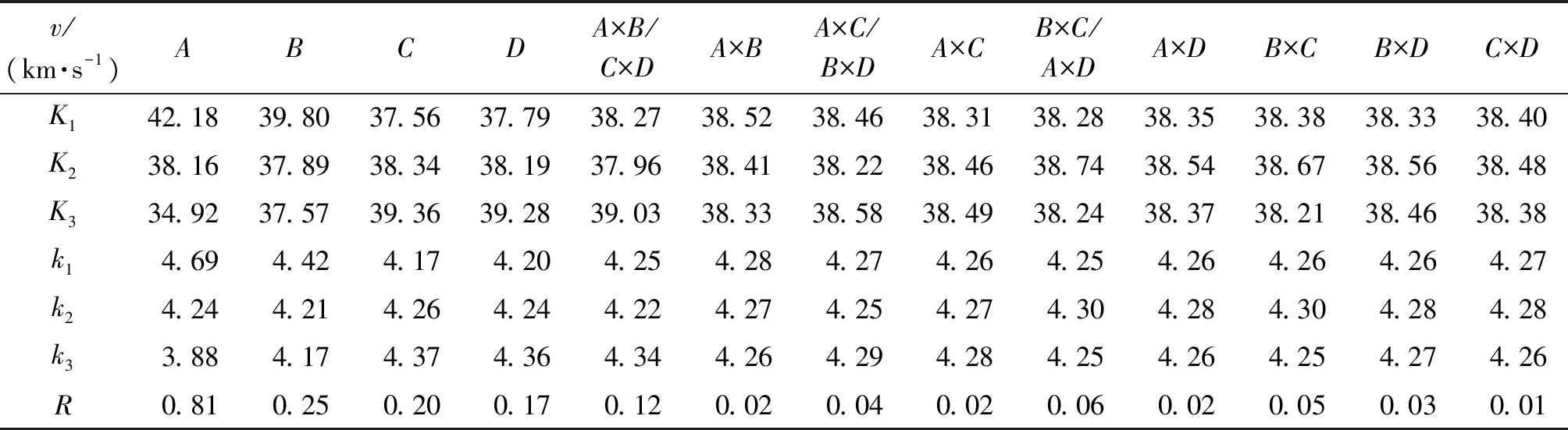
表8 极差表(头部速度为指标)Table 8 Range table (head velocity as index)

可以看出，对于头部速度这一考核指标，单因素的极差相较于交互作用的极差大，单因素对于考核指标的影响大于交互作用。容易得出，最优方案为1133(3号方案)。但考虑到交互作用××与因素的极差相差不是很大，这里再考虑××的影响进行分析。又、两个单因素极差远大于×，这里不再考虑二者的交互作用，只用考虑×，写出其搭配表，如表9所示，可知3×3、3×2以及2×3可以获得较大的速度，由于单因素相比×影响较大，且3最优，因此舍去2×3这一搭配方案，得到优化方案1132。因此，对于头部速度这一考核指标，优化方案有两个，即1133(3号方案)和1132。

表9 C×D搭配表(头部速度为指标)Table 9 Matching table of C×D (head velocity as index)

由于1132在已有27个试验中并无对应试验方案，对其进行建模和数值模拟，命名为30号试验方案。由表10可以看出，30号试验方案头部速度为4 999.6 m/s，相较于3号方案的5 009.1 m/s相差不大，但是头部直径明显较大，并考虑到3号方案截体间距大于30号方案的截体间距，在实际制造中会使用更多的外壳，因此优选30号方案1132为最优方案。对于头部速度的最优方案30号方案，其对应的无截体装药形成的射流直径为2.85 mm，直径提高了43%，射流速度下降了18%。3号方案和30号方案射流形态见图5所示。

6 结论

通过正交优化设计和数值模拟对带截体聚能装药进行分析，研究表明：① 使用尼龙作为截体材料可以使剩余射流断裂头部直径大幅增加，速度小幅度下降；② 对于剩余射流断裂头部直径指标，最优方案为27号方案，即罩锥角76°，罩壁厚1 mm，药顶高30 mm和截体间距10 mm，头部直径提高51.99%，头部速度下降23.44%；③ 对于剩余射流断裂头部速度，最优方案为30号方案，即罩锥角60°，罩壁厚0.75 mm，药顶高30 mm和截体间距17.5 mm，头部直径提高43%，头部速度下降18%；④ 对于以上两个优化方案还得结合炸高实验进行判断，为后续研究冲击裸药和带壳装药提供设计基础。