椭圆形截面杀伤战斗部破片初速分布特性研究

2022-04-08薛再清李国杰辛春亮

兵器装备工程学报 2022年3期

姜斌，沈波，薛再清，李国杰，乔良，辛春亮

(北京航天长征飞行器研究所，北京 100076)

1 引言

近年来，高升阻比气动外形技术正不断在新型飞行器中应用。由于飞行器形状的扁平化，战斗部必须向非圆化方向发展，以适应飞行器的装填空间。关于非圆截面战斗部的研究，目前已有的报道主要针对D形和多边形战斗部结构。王马法等通过对战斗部壳体在炸药内爆作用下的飞散过程进行分析，利用斜激波理论研究爆轰波对壳体的加速和变形作用，得到壳体的运动速度和方向，并进行了试验验证。Ding和李翔宇等对D形装药结构开展了一系列深入研究，提出了多种类型的D形装药结构设计方案，并通过数值仿真分析了不同种类D形装药结构的破片飞散特性，最后开展了静爆实验对D形装药结构威力场分析模型进行验证。Guo等研究了长径比及偏心起爆的偏心率对D形战斗部破片速度分布的耦合影响，分析出了D型战斗部破片受爆轰波驱动加载历程的影响。李元等针对不同结构特性的六棱柱装药结构的破片速度飞散特性开展了一系列数值分析与实验研究，为具有破片飞散密度增益的爆轰波控制式定向战斗部的应用提供丰富的数据基础。Ning等设计了一种可作为变几何装置组成部分的三棱柱形装药结构，通过数值仿真及静爆实验对炸药内爆作用下的破片飞散特性及破片对目标打击特性开展了相关研究，建立了破片飞散特性分析模型。综上所述，现已开展研究的非对称截面杀伤战斗部，其非对称面为平面或某一固定曲率值的曲面，还未见到有关变曲率截面的有关报道。

本文中提出了一种椭圆形截面杀伤战斗部结构，定义了该种装药结构下的结构特征参数，并据此建立了相应的数值计算模型，对不同扁率装药结构的起爆过程及破片飞散过程进行了数值模拟分析，研究结果可为类似战斗部的工程设计提供参考方法。

2 椭圆形截面战斗部结构模型

2.1 椭圆形截面战斗部结构参数定义

表1 椭圆形截面战斗部结构形状参数Table 1 The parameters of the ellipse warhead

图1 椭圆形截面战斗部结构示意图Fig.1 The schematic of the ellipse warhead

2.2 数值计算模型

依据上节所述战斗部的有关结构和尺寸，利用TrueGrid六面体网格划分软件建立椭圆形截面战斗部数值计算模型。辛春亮等的研究证实了炸药及其附近区域应划分细密网格以反映出足够频宽的冲击波特性，从而大大提高计算准确度，通过试算分析网格尺寸分别为3 mm、2.5 mm、2 mm和1.5 mm的计算结果，发现网格尺寸在2 mm时计算结果的收敛性已基本稳定，其既能满足计算精度又不过多增加计算时间，全模型剖面图和去掉空气、外壳体及上端盖的战斗部模型如图2。

图2 战斗部数值计算模型示意图Fig.2 The numerical model of warhead

运用LS-DYNA软件中的流固耦合算法模拟炸药爆炸及其对破片的驱动过程，其中炸药和空气域采用Euler算法，壳体和破片采用Lagrange算法。运用*ALE_MULTI_MATERIAL_GROUP关键字定义炸药和空气域的多物质组AMMG，以进行界面重构；运用*CONSTRAINED_LAGRANGE_IN_SOLID关键字定义炸药与破片和壳体的流固耦合作用。壳体与破片之间定义侵蚀面面接触，破片之间定义侵蚀单面接触，在空气域的边界设置压力外流边界条件。

本研究中的装药选用B炸药，状态方程采用JWL形式：

(1)

式中：为压强，为相对体积，为比内能，、、、、为常数，其数值如表2所示。

表2 炸药状态方程参数Table 2 The parameters of JWL model of Composition B

战斗部的内外层壳体和上下端盖均选用LY-12硬铝材料，采用*MAT_PLASTIC_KINEMATIC的各向同性硬化弹塑性材料模型。空气选用理想气体模型。各材料具体参数如表3～表5所示。

表3 LY-12硬铝材料参数Table 3 The parameters of LY-12

表4 空气材料参数Table 4 The parameters of air

表5 钨合金材料参数Table 5 The parameters of tungsten alloy

2.3 数值计算方法检验

根据文献[10]中对圆柱形战斗部的实验研究结果，本文中建立了如图3(a)所示的数值计算方法验证模型，从而验证上文所述的流固耦合计算方法以及相关材料的力学性能参数的合理性。破片飞散情形如图3(b)所示，利用后处理输出节点的速度信息，统计加速完全后每枚破片的速度，取其算数平均值为1 344.66 m/s，相较于试验测得的平均速度1 404.01 m/s，其相对误差为4.23%，可以认为本研究的数值计算方法能够很好地满足计算需求。

图3 数值模拟验证模型图Fig.3 The numerical model for validation

3 结果与讨论

3.1 数值计算结果

对椭圆形截面战斗部(=0.4)采用中心线起爆方式，起爆过程如图4所示，可以看出主装药起爆后，产生的高温高压爆轰产物气体随着爆轰波的传播向外膨胀，同时驱动破片向外飞散。椭圆形截面边界线具有变曲率的特点，靠近长轴方向的边界线曲率较大，随着破片的飞散，破片之间的间隙迅速变大，爆轰产物发生泄漏，靠近短轴方向的边界线曲率较小，破片之间的间隙变化缓慢，爆轰产物泄露较少。

图4 椭圆形截面战斗部起爆过程示意图Fig.4 The initiation process of an elliptical warhead

图5展示了起爆后300 μs时破片飞散的情形。从轴向视图可以看出，与传统回转体战斗部相比，椭圆形截面战斗部周向破片呈现不均匀分布，战斗部短轴方向的破片速度和密度均大于长轴方向，并随着扁率k值的增大，这种趋势愈发明显。从侧视图可以看出，装药结构靠近中间截面处会形成一段区域，该区域中的破片在同一时刻沿周向方向飞散的距离相等，即速度相等，飞散几乎不受轴向稀疏波的影响，为了便于讨论装药截面形状对破片周向飞散特性的影响，下文中所述的破片飞散速度均为中间层破片。

图5 300 μs时不同扁率的战斗部破片飞散示意图Fig.5 Schematic for fragment dispersion of different flattening warhead at 300 μs

3.2 装药结构破片初速度特性分析

椭圆形截面为1/4对称结构，针对不同扁率的战斗部，选取与x轴正方向夹角90°范围内的破片进行统计，得到破片速度分布曲线如图6。圆截面战斗部破片周向速度分布均匀，其平均值为1 815.49 m/s。按照表6中所示数值计算模型的装填质量值，采用Gurney公式计算出其破片飞散速度理论值为1 973.46 m/s，与统计得到的破片飞散速度平均值相比，其相对误差为8.7%，说明了本研究中的数值计算方法具有一定的可靠性。随着扁率的增加，战斗部自身装药量逐渐减少，装填比不断提高，导致破片速度呈现整体下滑。但是观察图6中圈选的短轴方向破片速度，发现存在高扁率大于低扁率的情况，分析其原因，主要得益于扁率增大导致短轴方向破片速度增益效果明显，弥补了整体速度降低带来的影响。

图6 破片速度分布曲线Fig.6 Fragment velocity distribution curve

表6 圆截面战斗部数值计算模型质量分布Table 6 Mass distribution of circular section warhead numerical calculation model

图7(a)为=04的椭圆形截面战斗部周向角分别为0°和90°处的2枚破片的速度曲线，=0°处的破片速度为1 430 m/s，=90°处的破片速度为1 727 m/s。为了进一步说明装药截面形状对破片加速过程的影响，对这两枚破片的速度进行求导，得到其加速度曲线如图7(b)。从图中可以看出，加速度曲线可以被划分为3个区域，即Ⅰ-Ⅲ区，区域Ⅰ可被视为爆轰波初始冲击加载过程，其中=90°处的破片由于距离起爆点较近，所以它首先具有加速度，由于=0°处的破片具有更大的驱动装药量，所以其获得的初始加速度更大；区域Ⅱ可被视为爆轰产物的驱动过程，=0°处的破片加速度急剧下降至0，而=90°处的破片维持在一段相当长的时间内具有加速度；区域Ⅲ中，由于大量的爆轰产物泄露及稀疏波的引入，2个方向的破片加速度均趋近于0。对比2个方向的破片加速过程，可以得到装药截面形状影响了爆轰产物对破片驱动的过程，=0°处破片所在位置的边界线曲率较大，破片间的间隙扩展迅速，爆轰产物还未对破片驱动完全就已大量泄漏，这也与图4中观察到的现象相吻合。

图7 不同周向角破片速度和加速度曲线Fig.7 Curve of fragment velocity and acceleration with time at different circumferential angels

为了对比研究扁率对长轴方向破片加速过程的影响，分别对4种扁率战斗部=0°处的破片速度进行求导，得到其加速度曲线如图8。4枚破片的加载历程大体相似，由于四枚破片到起爆点的距离相等，所以他们在同一时刻受到爆轰波加载获得加速度，但随值的增大，受爆轰波初始加载获得的加速度峰值逐渐降低，这是造成他们之间最终速度差异的重要原因。以分别为0和0.4为例，图9所示为=8 μs 时战斗部爆轰加载压力云图，为更直观感受=04的装药结构压力梯度，附加了炸药截面的压力云图。从图中可以看出由于圆截面的轴对称特性，其周向破片受到的爆轰波加载是均匀的，且在爆轰波刚抵达破片表面时，没有稀疏波对其强度造成干扰；而对于=04的装药结构，由于爆轰波会先斜入射驱动长轴方向两侧的破片，相应地会产生稀疏波追赶爆轰波阵面，造成爆轰波阵面强度被削弱，这就是不同扁率战斗部长轴方向破片获得的初始加速度峰值存在差异的原因。

图8 4种扁率战斗部长轴方向破片加速度曲线Fig.8 Curve of fragment acceleration with time in the long axis direction of four kinds of flattening warhead

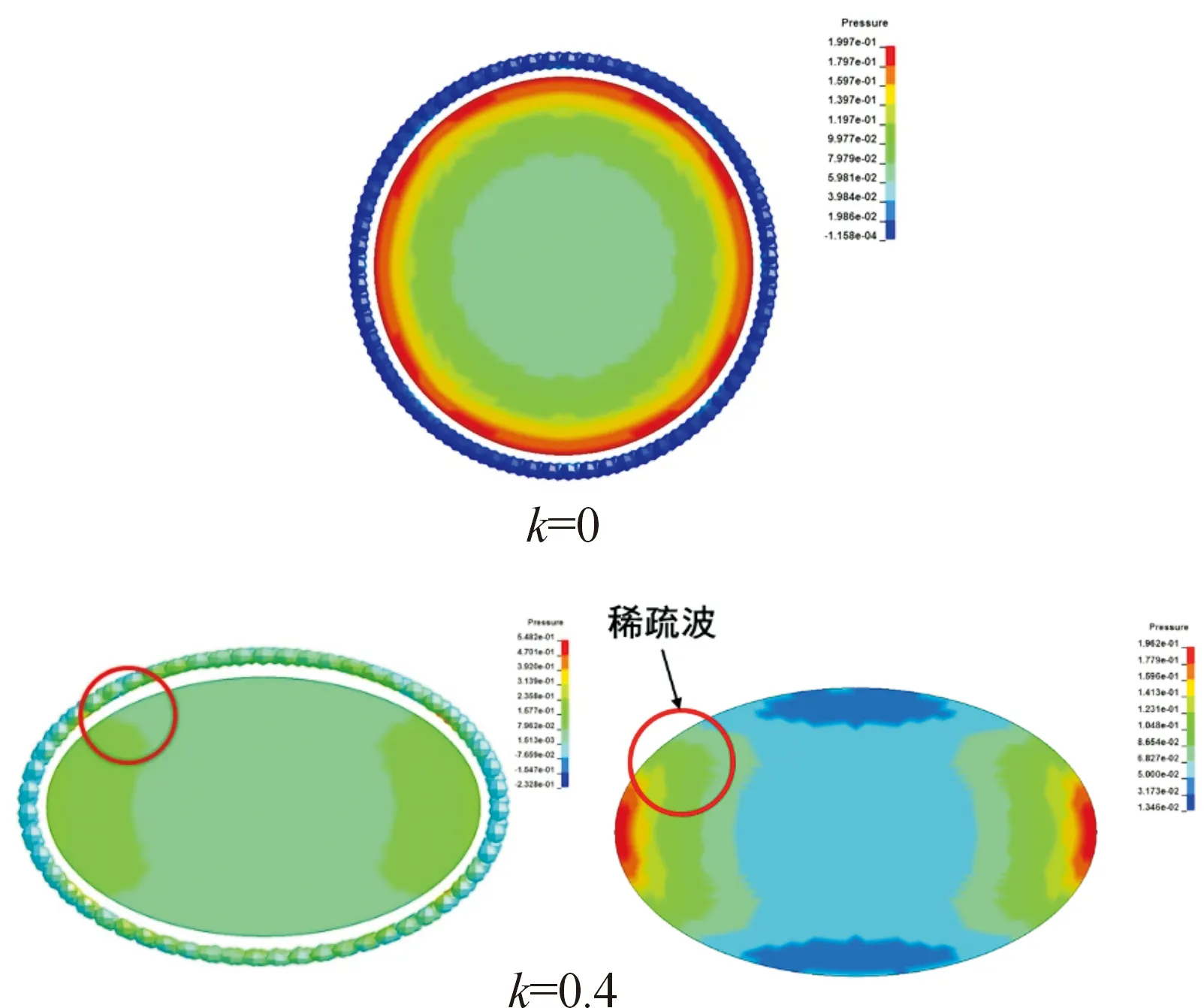
图9 t=8 μs时2种扁率战斗部爆轰加载压力云图Fig.9 Detonation loading pressure nephogram of two kinds of flattening warhead at 8 μs

3.3 基于一维等熵流体理论的破片驱动过程分析

上节已基于数值计算结果对椭圆形截面战斗部长轴和短轴方向破片的加速驱动过程进行定性分析，为更加准确判断破片经历的加速历程，采用爆炸对活塞的一维抛射理论对其定量分析。如图10(a)所示，以长轴方向破片驱动过程为例，将长轴方向的破片取为一宽度为的小微元，并假设破片微元两侧为刚性约束且破片微元为刚性。图10(b)为两等质量抛体在中心起爆下装药爆炸驱动过程。

图10 椭圆形截面战斗部一维抛射模型示意图Fig.10 One-dimensional projectile model of an elliptical warhead

爆轰产物的流动可以按照气体一维等熵流动的运动规律进行描述，当等熵指数取=3时，流动方程组可写为：

(2)

根据其特征线法，可得方程组的一般解为：

(3)

利用它可解出2个方向的扰动波交会后流场参数的变化规律。

已知爆轰波面后C-J参数分别为：

2区流场参数可由下式求解

(4)

上式中的任意函数(-)由抛体的运动规律确定。根据牛顿第二定律：

(5)

其中，为抛体的截面积，为运动速度，为作用在抛体壁面上的压力。由于

故

(6)

其中，为壁面处产物的声速。将上式代入式(5)后可得

(7)

其中，为炸药质量，=，为抛体质量。

已知各道右传波都是以自己的波速(+)传播，并且沿特征线，各道波速保持不变。因此，当其追赶上移动着抛体时便发生反射，在此瞬时，爆轰产物速度立即由降低为壁面处产物的速度，声速也立即变为壁面处产物的声速，故有

+=+

(8)

即

(9)

将式(7)代入上式得到

(10)

解此方程可得

(11)

(12)

将此结果代入式(11)后得到

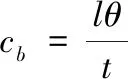
(13)

其中

(14)

将式(13)代入式(7)，积分

最后得到

(15)

此即为单一药柱一维接触爆炸驱动抛体的运动速度随时间变化规律，考虑到

则

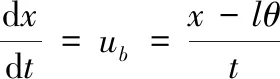
(16)

求解该式得到

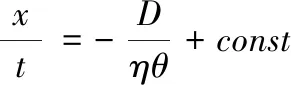
(17)

利用边界条件：=，=，便可解出被抛物体运动的轨迹为

(18)

从左侧抛体传回来的压缩波与运动着的右侧抛体在点相碰，因此点的参数可由下面两式联立求解

(19)

得到

(20)

将椭圆形截面战斗部(=04)长轴和短轴2个方向的和值分别代入上式可得-和-：

-=2586 μs，-=1478 μs

如图11所示，分别将2个时刻的对应点在加速度曲线上进行标记，可以发现当-=2586 μs时，长轴方向破片加速过程已接近完全，说明从其对侧破片反射回来的压缩波还未来得及对其作用，就由于稀疏波的过早引入衰减至没有驱动能力，其加载过程主要受2区的状态参数的影响。当-=1478 μs时，短轴方向破片刚刚经历了一段高加速度峰值的加速过程，其后续还将维持一段时间的持续加速过程，说明其受到了从对侧破片反射回来的压缩波的作用，其加载过程主要受2区和4区的共同影响。这也与上节中分析得到的长轴和短轴2个方向破片加速历程相符。