2022年高考立体几何复习及命题趋势预测

【摘 要】 本文通过对近三年立体几何考查内容分析、学生在立体几何中存在问题剖析和2022年高考立体几何10大热点问题预测等方面进行阐述，供考前备考参考.

【关键词】 立体几何;核心素养;全国卷;热点预测

立体几何研究的对象是现实世界中物体的形状、大小与位置关系，是高中数学教学的重要内容，也是高考考查的主要内容之一，其内容包含立体几何初步和空间向量两部分. 对于立体几何初步单元，《普通高中数学课程标准》[1]要求学生以长方体为载体，认识和理解空间点、直线、平面的位置关系;用数学语言表述有关平行、垂直的性质与判定，并对某些结论进行论证;了解一些简单几何体的表面积与体积的计算方法;运用直观感知、操作确认、推理论证、度量计算等认识和探索空间图形的性质，建立空间观念[2]. 对于空间向量单元，要求学生在学习平面向量的基础上，利用类比的方法理解空间向量的概念、运算、基本定理和应用，体会平面向量和空间向量的共性和差异，运用向量的方法研究空间基本图形的位置关系和度量关系，体会向量方法和综合几何方法的共性和差异，运用向量方法解决简单的数学问题和实际问题，感悟向量是研究几何问题的有效工具[3].下面我们从近三年考查立体几何内容分析、学生在立体几何中存在问题剖析和2022年高考立体几何10大热点问题预测等方面进行阐述，供考前备考参考.

1 近三年考查内容分析

1.从近年来全国各套高考数学试题来看，立体几何一般包括二至三道客观小题，一道两问的主观解答题，总分在22～27分之间，约占全卷总分的15%～18%，难度整体上相对保持稳定，难易适中，分文理科的题目相同，顺序微调，或者题干条件相同，问题稍有区别，难度差逐渐缩小，有利于文理同卷的平稳过渡.要求学生在不同的问题情景中，运用直观感知、操作确认、推理论证和度量计算等认识和探索空间图形的性质，能够依托空间向量建立空间图形及图形关系的想象力，建立空间观念，培养学生的直观想象、数学抽象、逻辑推理、数学运算、数学建模等核心数学素养[4，5].客观题以单项选择题、多项选择题或填空题呈现，除了涉及三视图，空间图形翻折，数学文化时给出图形外，其它情形一般不给出图形，主要考查画图、识图和用图的能力，侧重于简单几何体（柱、锥、台，球）或简单组合体基本量的计算，相关性质的考查等;主观解答题以简单几何体（柱、锥、台）或不规则几何体为载体，主要采用“一半证明、一半计算”相结合的模式，第一问侧重考查位置关系的证明，以垂直证明题型为主，考查学生的空间想象能力和逻辑推理能力，第二问侧重度量关系的计算，以角或距离的运算为主，解题方法一般包含综合几何方法或空间向量方法等两种以上的计算方法，要求学生灵活地选择解题方法，从不同的角度解决立体几何问题，其中一定有一种空间向量方法，要求学生能够运用空间向量解决一些简单的实际问题，体会用空间向量解决数学问题的思路.

2.近三年全国卷考查内容分析

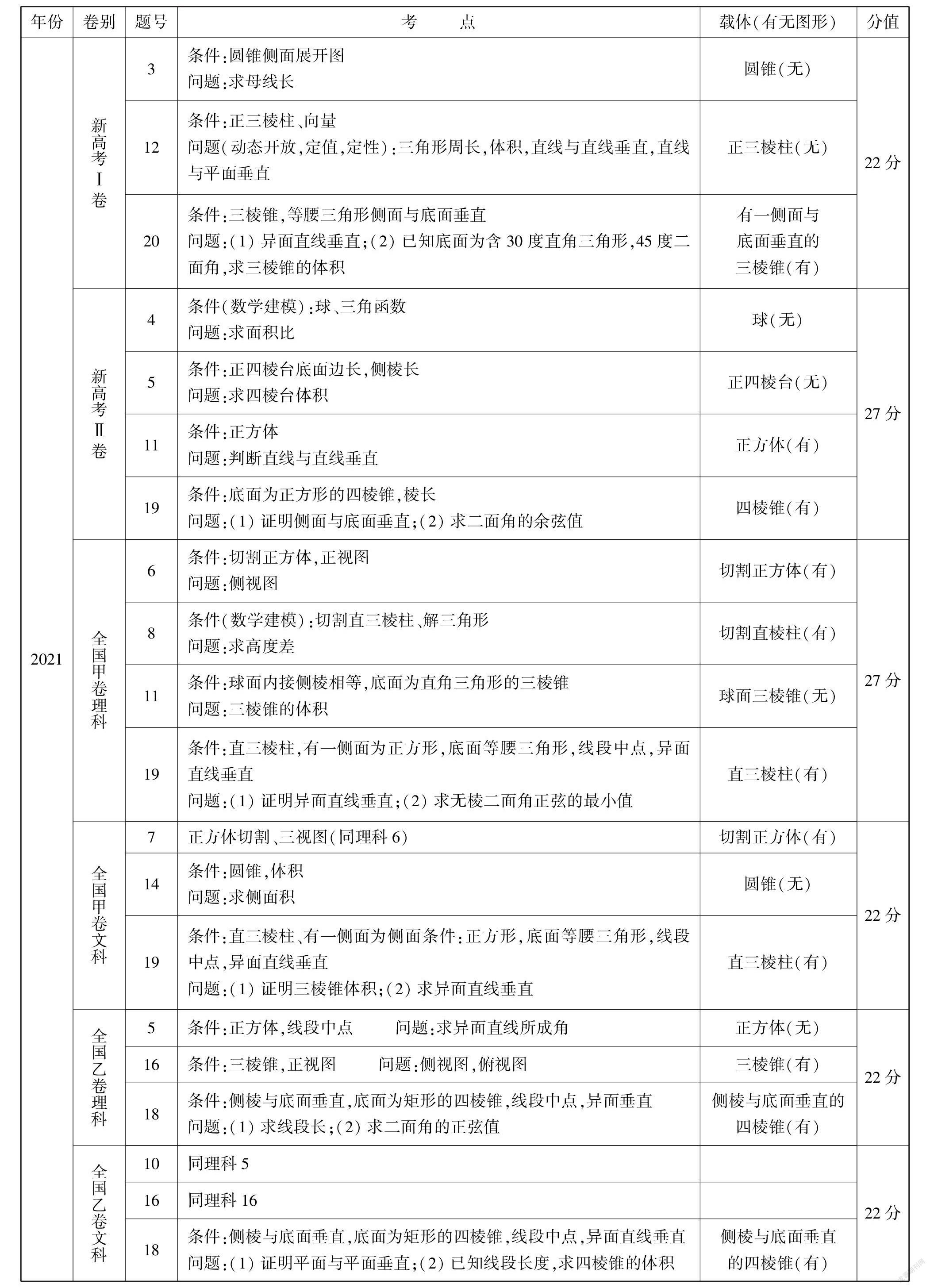
年份卷别题号考  点载体（有无图形）分值

2021

新高考Ⅰ卷

3条件：圆锥侧面展开图问题：求母线长圆锥（无）

12条件：正三棱柱、向量问题（动态开放，定值，定性）：三角形周长，体积，直线与直线垂直，直线与平面垂直正三棱柱（无）

20条件：三棱锥，等腰三角形侧面与底面垂直

问题：（1）异面直线垂直;（2）已知底面为含30度直角三角形，45度二面角，求三棱锥的体积有一侧面与底面垂直的三棱锥（有）22分

新高考Ⅱ卷

4条件（数学建模）：球、三角函数问题：求面积比球（无）

5条件：正四棱台底面边长，侧棱长问题：求四棱台体积正四棱台（无）

11条件：正方体问题：判断直线与直线垂直正方体（有）

19条件：底面为正方形的四棱锥，棱长问题：（1）证明侧面与底面垂直;（2）求二面角的余弦值四棱锥（有）27分

全国甲卷理科

6条件：切割正方体，正视图问题：侧视图切割正方体（有）

8条件（数学建模）：切割直三棱柱、解三角形问题：求高度差切割直棱柱（有）

11条件：球面内接侧棱相等，底面为直角三角形的三棱锥问题：三棱锥的体积球面三棱锥（无）

19条件：直三棱柱，有一侧面为正方形，底面等腰三角形，线段中点，异面直线垂直

问题：（1）证明异面直线垂直;（2）求无棱二面角正弦的最小值直三棱柱（有）27分

全国甲卷文科

7正方体切割、三视图（同理科6）切割正方体（有）

14条件：圆锥，体积问题：求侧面积圆锥（无）

19条件：直三棱柱、有一侧面为侧面条件：正方形，底面等腰三角形，线段中点，异面直线垂直

问题：（1）证明三棱锥体积;（2）求异面直线垂直直三棱柱（有）22分

全国乙卷理科

5条件：正方体，线段中点  问题：求异面直线所成角正方体（无）

16条件：三棱锥，正视图  问题：侧视图，俯视图三棱锥（有）

18条件：侧棱与底面垂直，底面为矩形的四棱锥，线段中点，异面垂直问题：（1）求线段长;（2）求二面角的正弦值

侧棱与底面垂直的四棱锥（有）22分

全国乙卷文科

10同理科5

16同理科16

18条件：侧棱与底面垂直，底面为矩形的四棱锥，线段中点，异面直线垂直问题：（1）证明平面与平面垂直;（2）已知线段长度，求四棱锥的体积侧棱与底面垂直的四棱锥（有）22分

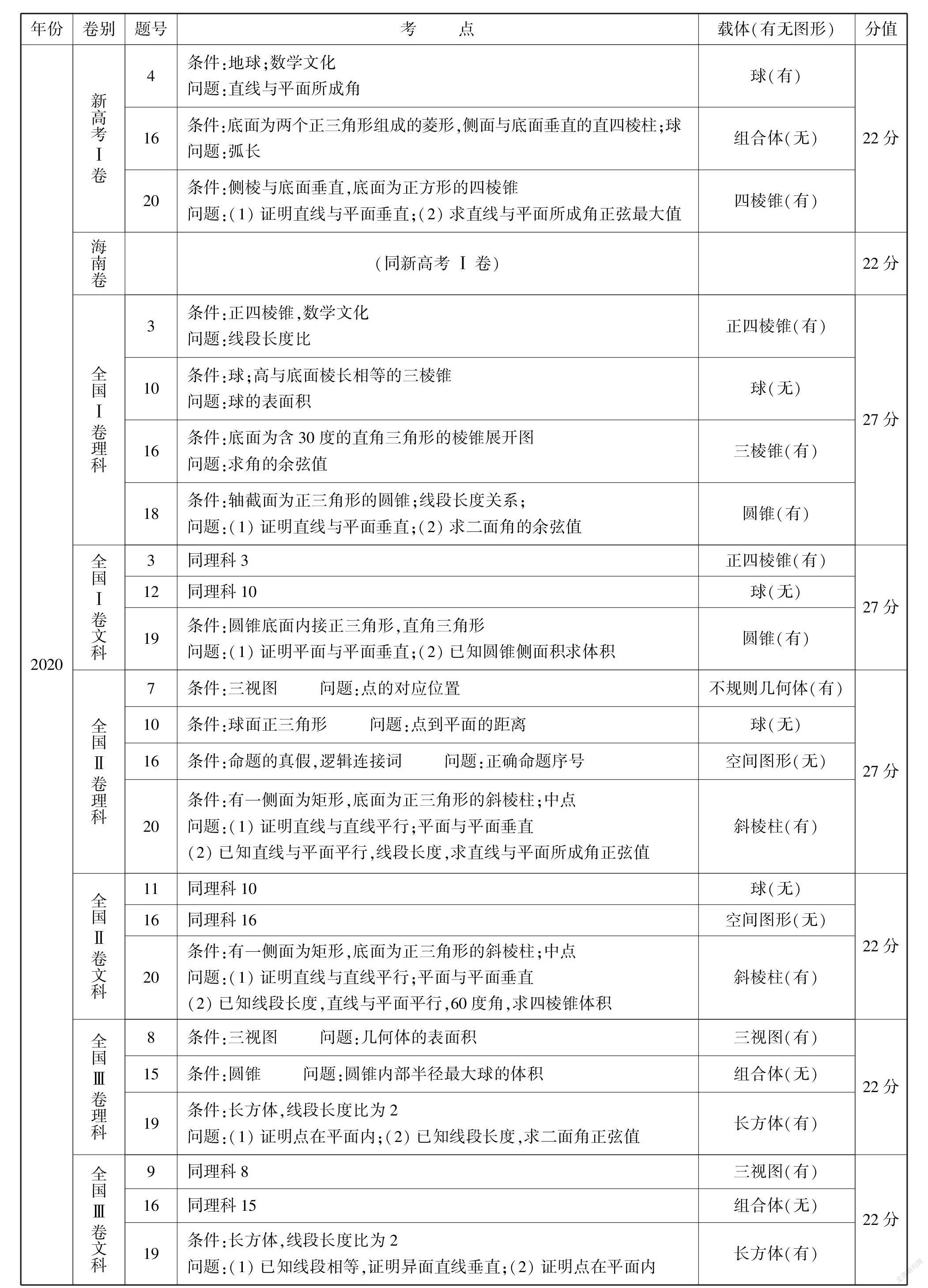
2020

新高考Ⅰ卷

4條件：地球;数学文化问题：直线与平面所成角球（有）

16条件：底面为两个正三角形组成的菱形，侧面与底面垂直的直四棱柱;球

问题：弧长组合体（无）20条件：侧棱与底面垂直，底面为正方形的四棱锥问题：（1）证明直线与平面垂直;（2）求直线与平面所成角正弦最大值四棱锥（有）22分

海南卷（同新高考Ⅰ卷）22分

全国Ⅰ卷理科

3条件：正四棱锥，数学文化问题：线段长度比正四棱锥（有）

10条件：球;高与底面棱长相等的三棱锥问题：球的表面积球（无）

16条件：底面为含30度的直角三角形的棱锥展开图问题：求角的余弦值三棱锥（有）

18条件：轴截面为正三角形的圆锥;线段长度关系;

问题：（1）证明直线与平面垂直;（2）求二面角的余弦值圆锥（有）27分

全国Ⅰ卷文科

3同理科3正四棱锥（有）

12同理科10球（无）

19条件：圆锥底面内接正三角形，直角三角形问题：（1）证明平面与平面垂直;（2）已知圆锥侧面积求体积

圆锥（有）27分

全国Ⅱ卷理科

7条件：三视图  问题：点的对应位置不规则几何体（有）

10条件：球面正三角形  问题：点到平面的距离球（无）

16条件：命题的真假，逻辑连接词  问题：正确命题序号空间图形（无）

20条件：有一侧面为矩形，底面为正三角形的斜棱柱;中点问题：（1）证明直线与直线平行;平面与平面垂直（2）已知直线与平面平行，线段长度，求直线与平面所成角正弦值斜棱柱（有）27分

全国Ⅱ卷文科

11同理科10球（无）

16同理科16空间图形（无）

20条件：有一侧面为矩形，底面为正三角形的斜棱柱;中点问题：（1）证明直线与直线平行;平面与平面垂直（2）已知线段长度，直线与平面平行，60度角，求四棱锥体积斜棱柱（有）22分

全国Ⅲ卷理科

8条件：三视图  问题：几何体的表面积三视图（有）

15条件：圆锥  问题：圆锥内部半径最大球的体积组合体（无）

19条件：长方体，线段长度比为2问题：（1）证明点在平面内;（2）已知线段长度，求二面角正弦值长方体（有）22分

全国Ⅲ卷文科

9同理科8三视图（有）16同理科15组合体（无）

19条件：长方体，线段长度比为2问题：（1）已知线段相等，证明异面直线垂直;（2）证明点在平面内长方体（有）22分

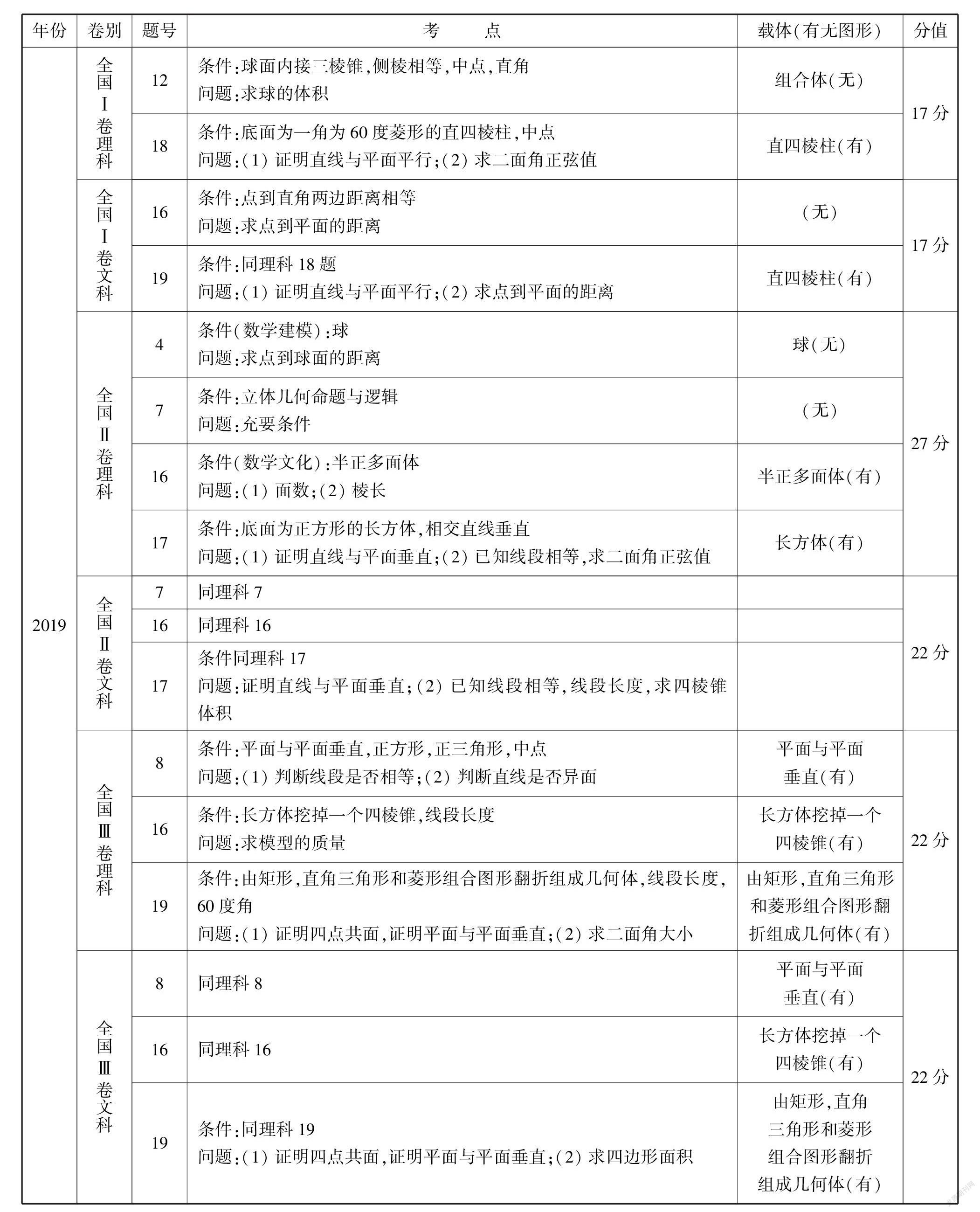
2019

全国Ⅰ卷理科

12条件：球面内接三棱锥，侧棱相等，中点，直角问题：求球的体积组合体（无）

18条件：底面为一角为60度菱形的直四棱柱，中点问题：（1）证明直线与平面平行;（2）求二面角正弦值直四棱柱（有）17分

全国Ⅰ卷文科

16条件：点到直角两边距离相等问题：求点到平面的距离（无）

19条件：同理科18题问题：（1）证明直线与平面平行;（2）求点到平面的距离直四棱柱（有）

17分

全国Ⅱ卷理科

4条件（数学建模）：球问题：求点到球面的距离球（无）

7条件：立体几何命题与逻辑问题：充要条件（无）

16条件（数学文化）：半正多面体问题：（1）面数;（2）棱长半正多面体（有）

17条件：底面为正方形的长方体，相交直线垂直问题：（1）证明直线与平面垂直;（2）已知线段相等，求二面角正弦值长方体（有）27分

全国Ⅱ卷文科

7同理科7

16同理科16

17条件同理科17问题：证明直线与平面垂直;（2）已知线段相等，线段长度，求四棱锥体积

22分

全国Ⅲ卷理科

8条件：平面与平面垂直，正方形，正三角形，中点问题：（1）判断线段是否相等;（2）判断直线是否异面平面与平面垂直（有）16

条件：长方体挖掉一个四棱锥，线段长度问题：求模型的质量长方体挖掉一个四棱锥（有）

19条件：由矩形，直角三角形和菱形组合图形翻折组成几何体，线段长度，60度角问题：（1）证明四点共面，证明平面与平面垂直;（2）求二面角大小由矩形，直角三角形和菱形组合图形翻折组成几何体（有）

22分

全国Ⅲ卷文科

8同理科8平面与平面垂直（有）

16同理科16长方体挖掉一个四棱锥（有）

19条件：同理科19问题：（1）证明四点共面，证明平面与平面垂直;（2）求四边形面积由矩形，直角三角形和菱形组合图形翻折组成几何体（有）22分

2 立体几何存在问题剖析

1.识图能力和用图能力弱. 对有几何图形的问题，几何图形观察不够，不能从平面几何中走出来，正确认识各元素的空间位置和图形的空间结构;不能正确从几何图形的直观图或三视图中想象对应的三维结构图，从中提取所需要的基本图形.

2.作图能力薄弱.对于没有图形的客观小题，不能作出满足题意的几何图形.作出的图形过大或过小都影响对几何体的观察;作出的图形中，实线和虚线不分.可见线都是实线，看不到的线都是虚线.基本作图能力的薄弱影响了学生对图形的观察与分析，制约了识图能力的提高.

3.三种数学语言的转换能力不强.立体几何包含自然语言、符号语言和图形语言三种语言.对于点、直线和平面之间的关系是用“∈”还是“”分辨不清;不能正確地进行语言间的转化，例如对应命题真假判定题型，给出符号语言，不能借助长方体图形或实物模拟实验进行判断.

4.逻辑推理不严谨.证明过程主观臆断，逻辑混乱;表达不准确，定理内容记忆不准确，使用定理时有漏写条件现象.5.运算不准确.在计算几何图形的面积或体积时用错公式;计算组合体的面积或体积时有漏算或多算现象;使用向量方法解题时，向量符号不加箭头，将点的坐标，法向量求错.

6.解题过程不完整.在解题过程中需要添加的辅助线不加说明;解题过程中出现条件中没有的字母;在利用空间向量解题时，建立空间直角坐标系之前需要证明垂直关系的没有进行论证;没有建立空间直角坐标系的过程或错用左手坐标系.3 2022年高考立体几何10大热点问题预测

热点1 与球相关问题

解答与球相关的问题时一般不需要画球，关键是定球心的位置（利用球的定义确定球心，补体确定球心或者利用两条垂线的交点确定球心），定球半径长，注意两点：（1）将球的问题化归为由球心和其它点组成的多面体问题解答;（2）用好球中垂径定理，R2=r2+d2，其中，R表示球半径长，r表示球截面圆的半径长，d表示球心距.在使用球中“垂径定理”解题时，注意几何体中三个关键点：（1）球心O;（2）截面Γ圆心O1;（3）截面Γ上的特殊点.

题1 已知球O的面上四点A，B，C，D，DA⊥平面ABC，AB⊥BC，DA=AB=BC=3，则球O的体积等于.

1.答案：9π2 .

题2 （单选题）已知平面α截一球面得圆M，过圆心M且与α成60°二面角的平面β截该球面得圆N.若该球面的半径为4，圆M的面积为4π，则圆N的面积为（  ）.

A. 7π   B.9π   C.11π   D.13π

2.答案：D.

热点2 与逻辑相关问题

以立体几何问题为载体的命题真假的判定题型，如果题目中没有给出图形，常常借助长方体图形或利用直尺纸张模拟试验排除不正确的命题.注意和充要条件相结合的立体几何命题真假的判定.

题3 （多选题）如图1，已知六棱锥PABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论正确的是（  ）.

A. PD⊥BF

B.线段PE的长是点P到直线DE的距离

C.过点C作直线AE的垂线，则此垂线必垂直于面PAE

D.直线PD与平面ABC所成的角为45°

3.答案：ABD.题4 （单选题）设α，β，γ为平面，m，n，l为直线，则m⊥β的一个充分条件是（  ）.

A.α⊥β，α∩β=l，m⊥l

B.α∩β=m，α⊥γ，β⊥γ

C.α⊥γ，β⊥γ，m⊥α

D.n⊥α，n⊥β，m⊥α

4.答案：D.

题5 （多选题）已知M是正方体ABCDA1B1C1D1的棱DD1的中点，下列结论正确的是（  ）.

A.过M点有且只有一条直线与直线AB，B1C1都相交

B.过M点有且只有一条直线与直线AB，B1C1都垂直

C.过M点有且只有一条直线与直线AB，B1C1都相交

D.过M点有且只有一条直线与直线AB，B1C1都平行

5.答案：ABD.

热点3 平行问题

平行问题是解答题中重要的证明题型，包含直线与直线平行，直线与平面平行，平面与平面平行.底面为平行四邊形，矩形，菱形，梯形等均含有平行关系.涉及线段中点的问题一般和三角形中位线定理、梯形中位线定理相联系.注意空间直线与直线平行的证明题型.

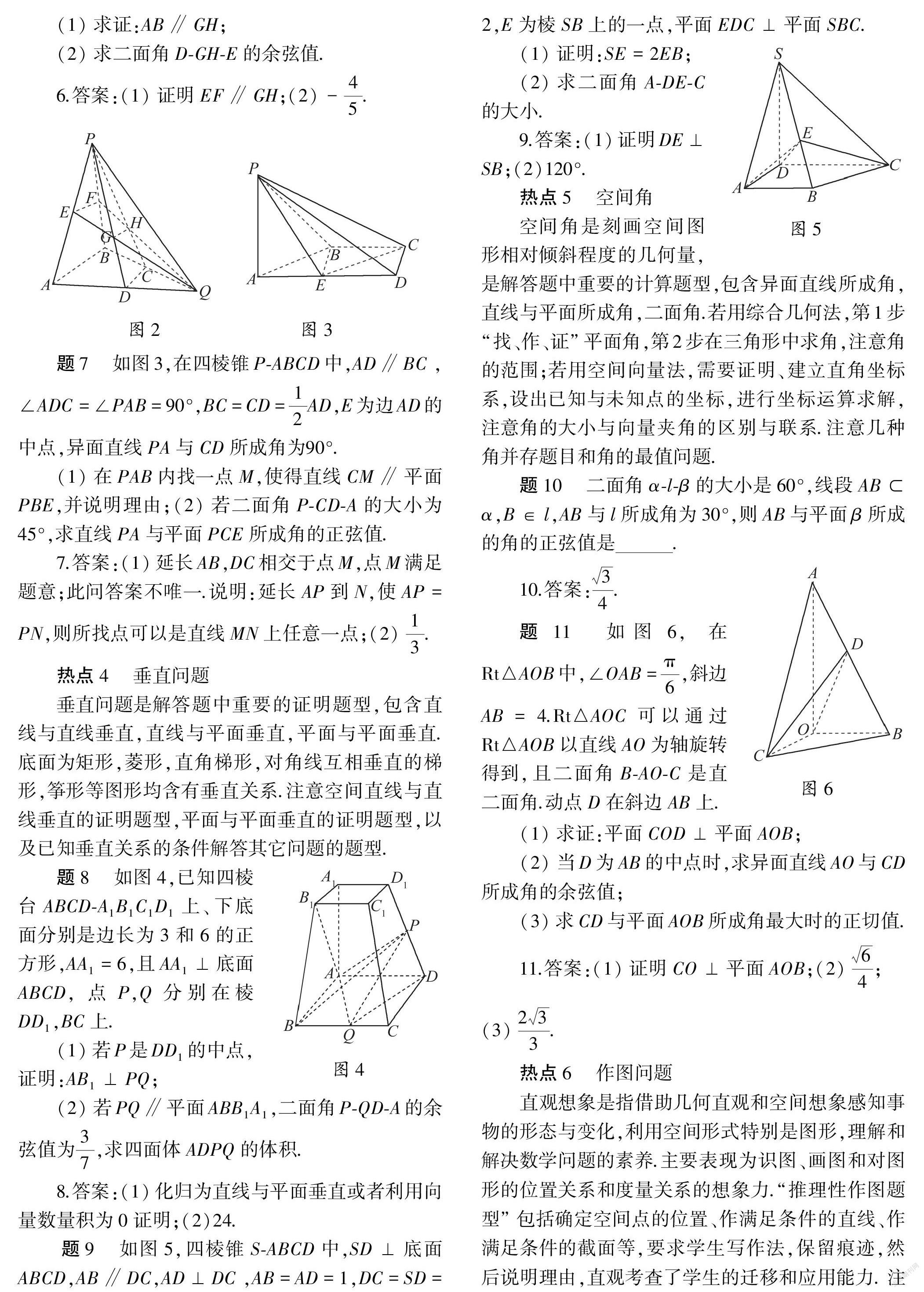
题6 如图2所示，在三棱锥PABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH.

（1）求证：AB∥GH;（2）求二面角DGHE的余弦值.

6.答案：（1）证明EF∥GH;（2）-45.

题7 如图3，在四棱锥PABCD中，AD∥BC ，∠ADC=∠PAB=90°，BC=CD=12AD，E为边AD的中点，异面直线PA与CD所成角为90°.

（1）在PAB内找一点M，使得直线CM∥平面PBE，并说明理由;（2）若二面角PCDA的大小为45°，求直线PA与平面PCE所成角的正弦值.

7.答案：（1）延长AB，DC相交于点M，点M满足题意;此问答案不唯一.说明：延长AP到N，使AP=PN，则所找点可以是直线MN上任意一点;（2）13.

热点4 垂直问题

垂直问题是解答题中重要的证明题型，包含直线与直线垂直，直线与平面垂直，平面与平面垂直.底面为矩形，菱形，直角梯形，对角线互相垂直的梯形，筝形等图形均含有垂直关系.注意空间直线与直线垂直的证明题型，平面与平面垂直的证明题型，以及已知垂直关系的条件解答其它问题的题型.图4

题8 如图4，已知四棱台ABCDA1B1C1D1上、下底面分别是边长为3和6的正方形，AA1=6，且AA1⊥底面ABCD，点P，Q分别在棱DD1，BC上.

（1）若P是DD1的中点，证明：AB1⊥PQ;

（2）若PQ∥平面ABB1A1，二面角PQDA的余弦值为37，求四面体ADPQ的体积.

8.答案：（1）化归为直线与平面垂直或者利用向量数量积为0证明;（2）24.

题9 如图5，四棱锥SABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC ，AB=AD=1，DC=SD=2，E为棱SB上的一点，平面EDC⊥平面SBC.图5

（1）证明：SE=2EB;（2）求二面角ADEC的大小.

9.答案：（1）证明DE⊥SB;（2）120°.

热点5 空间角

空间角是刻画空间图形相对倾斜程度的几何量，是解答题中重要的计算题型，包含异面直线所成角，直线与平面所成角，二面角.若用综合几何法，第1步“找、作、证”平面角，第2步在三角形中求角，注意角的范围;若用空间向量法，需要证明、建立直角坐标系，设出已知与未知点的坐标，进行坐标运算求解，注意角的大小与向量夹角的区别与联系.注意几种角并存题目和角的最值问题.

题10 二面角αlβ的大小是60°，线段ABα，B∈l，AB与l所成角为30°，则AB与平面β所成的角的正弦值是.图6

10.答案：34.

题11 如图6，在Rt△AOB中，∠OAB=π6，斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角BAOC是直二面角.动点D在斜边AB上.

（1）求证：平面COD⊥平面AOB;

（2）当D为AB的中点时，求异面直线AO与CD所成角的余弦值;

（3）求CD与平面AOB所成角最大时的正切值.

11.答案：（1）证明CO⊥平面AOB;（2）64;（3）233.热点6 作图问题

直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.主要表现为识图、画图和对图形的位置关系和度量关系的想象力.“推理性作图题型”包括确定空间点的位置、作满足条件的直线、作满足条件的截面等，要求学生写作法，保留痕迹，然后说明理由，直观考查了学生的迁移和应用能力. 注意利用几何中的公理、判定定理和性质定理等结论进行操作确认和推理认证.图7

题12 如图7，已知正三棱锥PABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连结PE并延长交AB于点G.

（1）证明：G 是AB的中点;（2）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积.

12.答案：（1）证明PG⊥AB;（2）在平面PAB内，过E作PB的平行线交PA于点F，F为点E在平面PAC内的正投影F;（3）四面体PDEF的体积为43.

题13 如图8，在三棱柱ABCA1B1C1中，侧棱AA1⊥底面ABC，AB=AC=2AA1，∠BAC=120°，D，D1分别是线段BC，B1C1的中点，P是线段AD的中点.

（1）在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1;

（2）设（1）中的直线l交AB于点M，交AC于点N，求二面角AA1MN的余弦值.

13.答案：（1）在平面ABC内，过点P作直线l∥BC，然后论证;（2）155.

热点7 距离问题

空间距离是刻画空间图形相对远近程度的几何量，是解答题中重要的计算题型，包含两点间的距离（含多面体和旋转体表面上两点间最短距离）、点到直线间的距离、点到平面间的距离、直线与直线间的距离、直线与平面间的距离和平面与平面间的距离等.求距离时，若用综合几何法，第1步利用平面与平面垂直的性质定理或相关结论确定垂足位置，第2步解三角形求距离线段的长;若用空间向量法，利用相关距离公式计算求解.注意“等积法”求点到直线的距离和点到平面的距離.题14 在正三棱柱ABCA1B1C1中，AB=1.若二面角CABC1的大小为60°，则点C到平面ABC1的距离为.

14.答案：34.

题15 在棱长为2的正方体ABCDA1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为.

15.答案：255.

热点8 动态几何问题

立体几何动态问题包括空间点的运动、平面图形的翻折、几何体的平移和旋转等，解答此类问题要注意运动前后有关几何元素的“不变性”与“不变量”. 注意点的运动轨迹问题，对于求相关几何量的范围或最值问题时常常和基本不等式、函数、导数等知识相关联.

题16 （单选题）在梯形ABCD中，∠ABC=π2，AD∥BC，BC=2AD=2AB=2.

将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为（  ）.

A.2π3   B.4π3

C.5π3   B.2π

16.答案：C.

题17 如图9，在三棱锥PABC的平面展开图中，AC=1，AB=AD=3，AB⊥AC，AB⊥AD，∠CAE=30°，则cos∠FCB=.

17.答案：-14.

题18 （单选题）正方体ABCDA1B1C1D1的棱长为2，动点E，F在棱A1B1上，动点P，Q分别在棱AD，CD上，若EF=1，A1E=x，DQ=y，DP=z，（x，y，z大于零），则四面体PEFQ的体积（  ）.

A.与x，y，z都有关

B.与x有关，与y，z无关

C.与y有关，与x，z无关

D.与z有关，与x，y无关

18.答案：C.

题19 如图10，已知平面四边形ABCD中，AB=BC=3，CD=1，AD=5，∠ADC=90°.沿直线AC将△ACD翻折成△ACD′，直线AC与BD′所成角的余弦的最大值是.

19.答案：69.热点9 开放型题型

立体几何中开放性问题包括存在型、举例型和结构不良型等，这需要学生根据题目条件去探索结论成立的条件，或者根据结论去探究问题成立的条件.对于存在型问题可以先猜后证或者利用空间向量法计算解答.

题20 已知正方形ABCD中，E、F分别是AB、CD的中点，将△ADE沿DE折起，如图11所示，记二面角ADEC的大小为θ（0<θ<π）.

（1） 证明BF∥平面ADE;

（2）若△ACD为正三角形，试判断点A在平面BCDE内的射影G是否在直线EF上，证明你的结论，并求角θ的余弦值.

20.答案：（2）点A在平面BCDE内的射影G在直线EF上， cosθ=14.

题21 如图12，在四棱锥PABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3.E为PD的中点，点F在PC上，且PFPC=13.

（1）求证：CD⊥平面PAD;（2）求二面角FAEP的余弦值;（3）設点G在PB上，且PGPB=23.判断直线AG是否在平面AEF内，说明理由.

21.答案：（1） 33;（2） 直线AG在平面AEF内.

热点10 数学文化与数学建模

数学模型搭建了数学与外部世界联系的桥梁，把数学问题与生活情境相结合，让数学生活化，生活数学化，使学生在实际生活中体会到数学的用途，并运用所学的知识，解决实际问题. 将考查方式与育人方式相结合，通过真实的几何问题情境体现数学的核心价值.题22 我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸. 若盆中积水深九寸，则平地降雨量是寸.

（注：①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸）

22.答案：3.

题23 （单项题）《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱，若阳马以该正六棱柱的顶点为顶点，以AA1为底面矩形的一边，则这样的阳马的个数是（  ）.

A.4   B.8   C.12   D.16

23.答案：D.

立体几何知识点的考查覆盖面广，且形式多样，选择题、填空题和解答题三类题型，一应俱全.在注重考点全覆盖的基础上，以考查点、线、面的位置关系为主线，既重点考查了有关线面平行与垂直关系的判断等必备知识，又通过角度求解、距离计算和面积体积计算等考查学生的关键能力与学科素养，以中档试题为主，体现“通过立体几何的基本图形，在考查必备知识的基础上，注重对通性、通法的考查”的命题思路.

参考文献

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.5.

[2] 人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 普通高中教科书（必修2）[M].北京：人民教育出版社，2020.

[3] 人民教育出版社，中学数学课程教材研究开发中心. 普通高中教科书（选择性必修1）[M].北京：人民教育出版社，2020.

[4] 教育部考试中心.聚焦核心素养 考查关键能力——2021年高考数学全国卷试题评析[J].中国考试，2021（07）：7076.

[5] 教育部考试中心. 以评价体系引领内容改革 以科学情境考查关键能力——2020年高考数学全国卷试题评析[J].中国考试，2020（08）：2934.

作者简介 刘才华（1969—），山东宁阳人，泰山名师，市学科带头人，中学高级教师;发表论文260余篇.