飞行Ma12 条件超燃发动机流场及燃烧特征分析
2022-04-07何粲邢建文欧阳浩邓维鑫肖保国
何粲 邢建文,†,1) 欧阳浩 邓维鑫 肖保国,†
* (中国空气动力研究与发展中心空天技术研究所,四川绵阳 621000)
† (中国空气动力研究与发展中心高超声速冲压发动机技术重点实验室,四川绵阳 621000)
引言
飞得更高更快一直是人类不断追寻的目标,作为飞行器的心脏,发动机可以说是制约其速度的核心部件.多年来,吸气式超燃冲压发动机凭借其简单构型、不需携带氧化剂等诸多优点一直是高超声速飞行器的理想推进系统之一.目前国内针对超燃冲压发动机的研究按照飞行马赫数范围可以分为两部分,首先是飞行马赫数4~ 7 的双模态超燃冲压发动机,其次是飞行马赫数Ma≥7 的高马赫数超燃冲压发动机[1].
经过60 多年的研究,双模态超燃冲压发动机关键技术逐渐被突破,在飞行演示试验中已能克服燃烧室的内阻和飞行器的外阻,产生正推力,即将进行工程应用[2-4].高马赫数超燃冲压发动机可用作大气层内超高速、高机动飞行器和可重复使用、低成本空天运输系统动力系统的一部分,有助于进一步提高高超声速武器的突防能力,具有极高的军事和民用价值.但与低马赫数超燃冲压发动机不同,高马赫数超燃冲压发动机仍然面临诸多关键科学和工程技术难题.因此,超燃冲压发动机下一步的重点研究方向之一是在现有超燃冲压发动机的研究基础上将其工作速域向上拓展,开展高马赫数超燃冲压发动机研究.
高马赫数超燃冲压发动机与马赫数4~ 7 发动机相比有以下几个特点:(1)燃烧室入口气流速度更高,通常在1500 m/s 以上,更高的流动速度给燃料混合、点火和燃烧组织带来了更大的难度;(2)阻力更大,更难实现推阻平衡,导致对混合和燃烧效率有更高的要求;(3)来流总温更高,燃烧室的热负荷急剧上升,发动机热防护技术更加困难.这些特点使得高马赫数超燃冲压发动机的研究极具挑战性,需要数值模拟、地面试验以及飞行试验的强有力结合才可能取得突破性进展.
以日本M12 系列及澳大利亚RESTM12 模型发动机[5]为代表,目前国外对高马赫数的发动机已经开展了一系列试验[6]与计算研究[7].其中M12 系列的研制目的是获得设计点为Ma12,工作范围为Ma10~ 15 的超燃冲压发动机.M12 系列发动机均为2D 构型,其研制经历了一个不断优化改进的过程,相较于M12-01[8],M12-02 做了两方面的改进[9].一是增加进气道压缩比,以提升燃烧室入口气流的静温(提升至1400 K)和密度;二是应用hypermixer 进行燃料喷注,以增强燃气掺混,改善发动机的稳焰特性和点火能力[10].
M12-02 开展了总焓为4,5,7,9 MJ/kg,分别对应飞行马赫数9,10,12,14,4 种工况条件下的试验.试验结果表明M12-02可以获得稳定且强烈的燃烧,燃烧带来的压升幅度增加且强燃烧时间延长,在高焓条件下的燃烧室性能相较于M12-01 得到显著改善.燃烧室性能随着气流总焓增加而提高,在设计点7 MJ/kg 时获得最佳性能.研究结果为改善高焓条件下超燃冲压发动机燃烧室性能提供了参考与支撑.但需要注意的是,结果也显示随着来流速度的进一步增加,M12-02 燃烧室性能将急剧下降[10].同时CFD 预测在M12-02 燃烧室出口燃气温度超过2600 K 时,由燃气热离解导致的净释热损失很显著[11].
近年来,国内针对飞行马赫数7 以上的高马赫数发动机也开展了一些地面试验及计算的研究,姚轩宇等[12]基于力学所JF12 长试验时间激波风洞开展了Ma7.0和Ma9.5 的氢燃料点火和燃烧试验.卢洪波等[13]在航天十一院FD-21 高能脉冲风洞完成了模拟Ma8,高度31 km 飞行条件的超燃试验.周建兴[14]等构造了一种圆截面高马赫数发动机并评估了其在Ma7~ 10 内的性能.Zhang和Li[15]针对M12-02 发动机开展了计算与分析[16].
中国空气动力研究与发展中心针对高马赫数发动机开展了建模与计算研究[17],以及基于不同燃料的一系列点火和燃烧地面试验[18-22].从以往研究可知,对于高马赫数发动机内流动及燃烧特性彻底理解尚有距离,计算与试验能力均有待进一步提升.本文将基于AHL3D 软件平台开展针对高马赫数发动机的计算方法改进与验证,并针对M12-02 发动机[23]不同状态进行三维数值模拟,验证改进后的方法对于该类高马赫数发动机的模拟能力,分析高马赫发动机内波系、参数分布及燃烧性能的特征.
1 数值模拟方法及验证
1.1 数值模拟方法
本文基于AHL3D 软件对发动机开展三维定常计算.AHL3D 软件平台可以模拟二维或三维、定常或非定常、完全气体或化学非平衡流动[24],可以对激波边界层干扰[25]、稳焰、燃烧[26]等复杂现象进行模拟,其对超燃冲压发动机的计算能力得到了大量算例的验证.这里简单介绍使用的控制方程与求解方法.
采用求解直角坐标系下的三维N-S 方程,形式如下

式中,Q=(ρ,ρu,ρv,ρw,ρEt,ρYi)T,E,F,G表示无黏通量,Fv,Gv,Ev表示黏性通量,S为源项,u,v,w为x,y,z方向速度,ρYi表示气体的密度和组份的质量分数,气体的总内能Et=e+(u2+v2+w2)/2,其中e表示热力学内能.
求解三维化学反应控制方程采用隐式有限体积法离散,无黏通量为AUSM PW+格式,黏性通量的计算方法采用Gauss 定理构造方法.湍流模型采用考虑可压缩性修正的wilcox2006 两方程湍流模型[27].
1.2 可压缩修正湍流模型
流体的可压缩性对湍流的演变有很大的影响,尤其是脉动压力和脉动速度散度之间的相关(或称压力-散度项)、可压缩性引起的湍流动能的耗散率(或称可压缩性耗散率)的影响最为重要,但在常规两方程模型中未考虑这两项的影响,本文对计算软件进行了基于wilcox2006 模型[27]的可压缩性修正.
考虑可压缩修正的wilcox2006 两方程湍流模型为

考虑膨胀耗散和压力膨胀的Sarkar可压缩修正时,对应的参数

1.3 激波串算例验证
算例是Waltrup 经典圆截面隔离段试验[28]中的一个模型,其直径69.85 mm,长度578 mm.计算采用的网格如图1 中所示,网格总量288 万,壁面网格距离1.0 μm.

图1 隔离段网格Fig.1 The grid of the isolator
计算状态为:来流马赫数2.6,总温289 K,进口总压为3.06 atm (1 atm=101.3 kPa),进口静压为0.15 atm,出口静压为1 atm.分别采用原始wilcox2006 湍流模型及经过可压缩修正的湍流模型对隔离段进行计算,将计算所得壁压与试验压力对比如图2 所示.
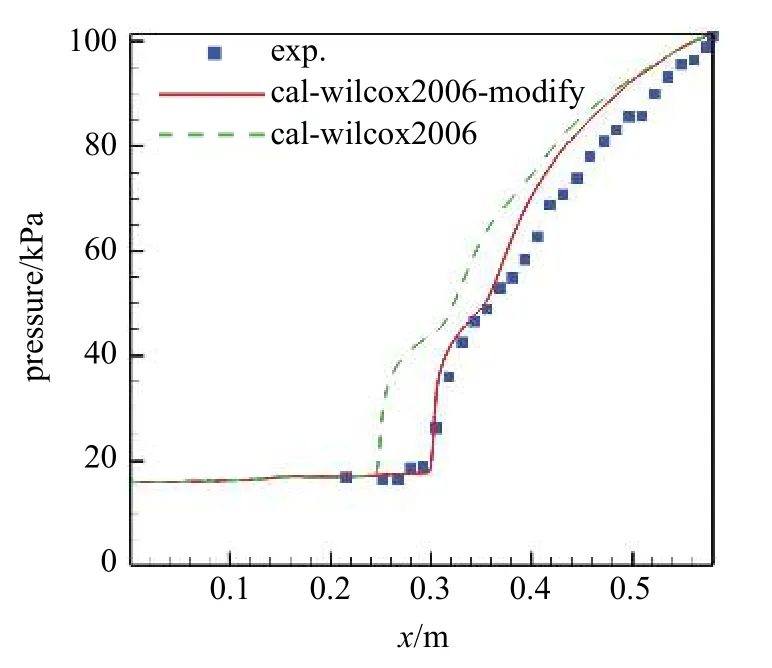
图2 采用经过可压缩修正的湍流模型与原始模型计算所得压力与试验对比Fig.2 Comparison of simulations to experimental pressures with compressible modified turbulence model and initial model
可见湍流模型经过Sarkar可压缩修正后,压力分布与试验结果更加吻合,经过可压缩修正的湍流模型更加准确地预测了的激波串位置.
2 高马赫数超燃冲压发动机冷态及燃烧模拟
基于AHL3D 软件平台,选用进行可压缩修正后的湍流模型对日本M12-02 高马赫数超燃冲压发动机开展冷态与燃烧状态的三维数值模拟,并对不同状态下发动机内流场结构、燃烧释热、推阻特性等进行分析.
2.1 物理模型
本文针对图3 所示日本的M12-02 发动机开展研究.发动机总长2.9 m,由二维侧压式进气道、平行段、等直燃烧室及扩张喷管组成.进气道入口截面尺寸为0.25 m × 0.2 m.进气道与扩张喷管的顶部与底部均为平板,侧壁与来流夹角分别为7.4°及8.9°.等直燃烧室长1.7 m,宽0.070 7 m.

图3 M12-02 发动机构型[23]Fig.3 Configuration of M12-02 scramjet model[23]
燃料为氢气,为增强混合采用流向涡支板进行燃料喷注,喷注系统详细结构如图4 所示[23],喷注装置位于进气道之后平行段的侧壁上.模拟氢气燃烧时采用13 组分33 方程简化模型[29].壁面采用无滑移壁面条件,考虑为等温壁,壁温为300 K.
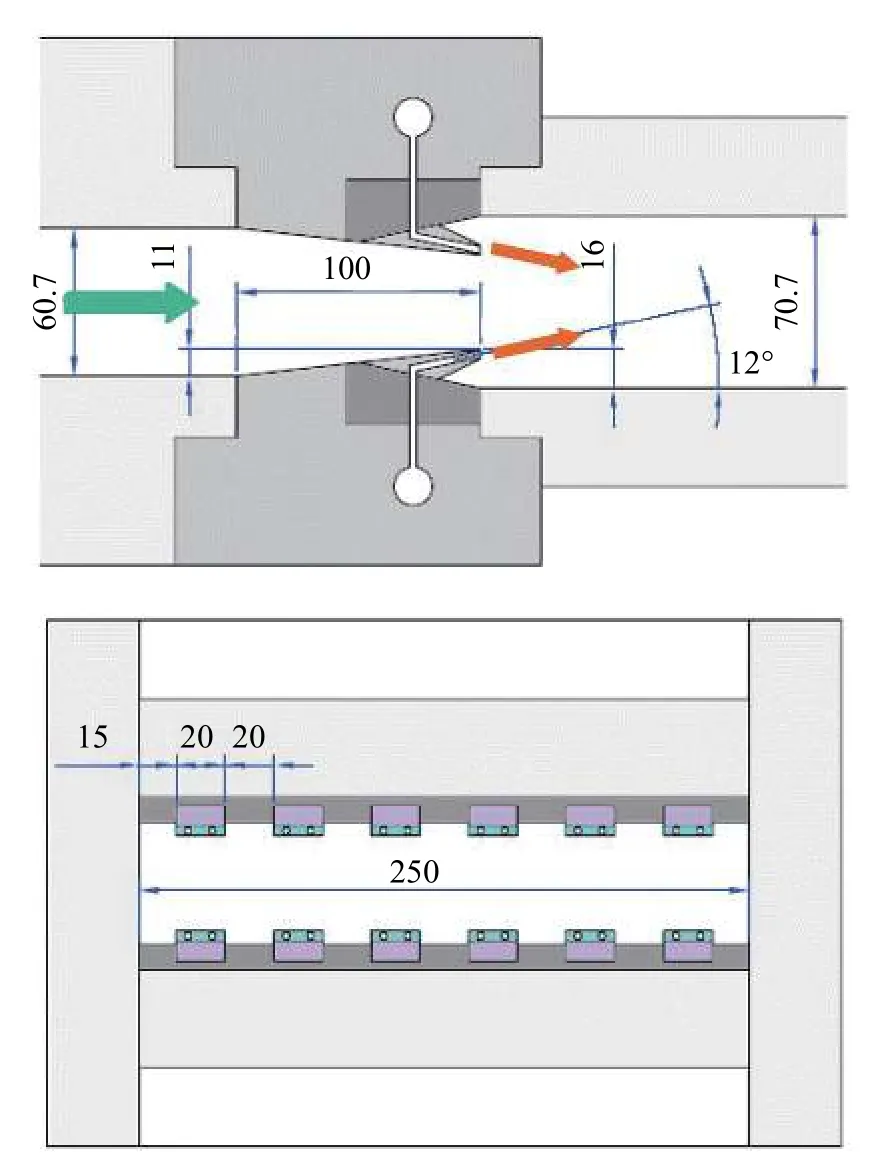
图4 M12-02 喷射模块结构[23]Fig.4 Injector structure of M12-02 scramjet[23]
由于所研究的高马赫数发动机构型沿展向(z方向)对称,为减少计算量,采用半模计算,总网格量约3000 万,如图5 所示.为能准确模拟边界层流动,壁面法向第一层网格高度为1 μm,以确保y+≤ 1.来流边界固定为来流参数,出口采用外推.计算过程收敛判断准则为:流场结构不再明显改变,密度最大残差下降3 个量级如图6 所示,入口流量+喷油量与出口流量差别小于2%,继续计算2 万步后流量变化量小于0.2%.

图5 M12-02 模型计算网格Fig.5 The mesh topology of M12-02 model

图6 密度残差收敛曲线Fig.6 Convergence curve of density residual
2.2 计算与试验的对比验证
针对上文介绍的发动机模型开展三维定常数值计算,计算状态与M12-02 发动机地面试验状态保持一致,进气道入口马赫数为6.72,速度为3480 m/s,静压4.0 kPa,静温677 K,氮气与氧气质量分数分别为0.203 1 与0.796 9.分别采用未经过可压缩修正的wilcox2006 模型与经过可压缩修正的wilcox2006 模型对发动机的冷态与燃烧状态(当量比(equivalence ratio,ER) 0.5和1.0)进行三维数值模拟,计算所得壁面压力与文献中的试验数据进行对比,如图7 所示.
从图7(a)中冷态下的压力分布可以看出,采用经过可压缩修正的湍流模型后,软件对该类问题的模拟能力明显增强,计算所得壁面压力波动位置及幅度均与试验值吻合良好.图7(b)中则给出了当量比1 条件下氢气燃烧状态下的壁压对比,可见增加了可压缩修正后,燃烧室后部的压力与试验值吻合得相对更好.

图7 采用经过可压缩修正的湍流模型与原始模型计算所得压力与试验对比Fig.7 Comparison of simulations to experimental pressures with compressible modified turbulence model and initial model
图8 中对称面波系分布更直观地展示了原始模型与修正后模型计算所得激波及其反射波系的差别.可见经过可压缩修正后计算所得激波角更大,且差异在经过多次激波反射后被放大,燃烧室后部的反射激波位置与原始模型结果相比已存在不可忽略的明显区别,修正后的模型计算所得激波位置与试验吻合更好.同时对比两种模型所得激波后高压区范围,可见头两道激波后高压范围相差不大,但对于后续反射激波,修正后的湍流模型计算得到的高压区域更大,反映了反射激波强度更大,激波带来的压升与试验值吻合也更好.
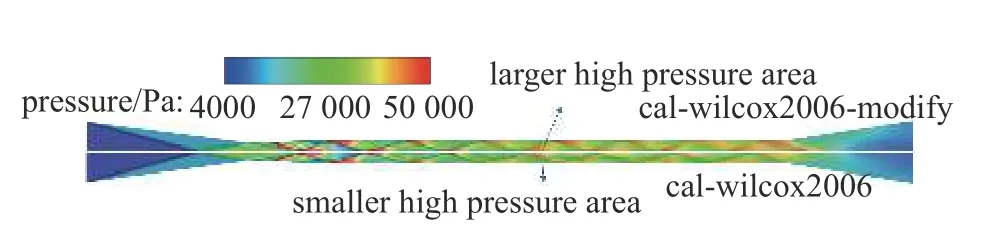
图8 采用经过可压缩修正的湍流模型与原始模型计算所得压力云图对比Fig.8 Comparison of numerical pressure with compressible modified turbulence model to initial model
总的来说,计算结果验证了经过可压缩修正的程序对该类高马赫数问题具有较好的模拟能力.
2.3 发动机内波系结构及参数分布特征
对于固定来流条件的高马赫数超燃冲压发动机,未注油的冷态情形下发动机内激波、膨胀波波系主要由流道结构决定.如图9 中对称面马赫数及波系云图可见,冷态时进气道入口处形成上下对称的激波,进气道与平行段转折处形成膨胀波,入口激波与注油位处收缩转折带来的激波一同在上下壁面之间反射,等直燃烧室内形成贯穿流道的反射波系,直至喷管扩张处形成膨胀波.
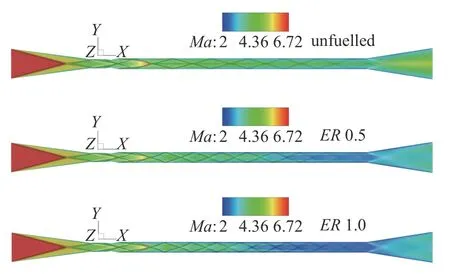
图9 不同状态下对称面马赫数及波系云图Fig.9 Centerline planes of Mach number and shock systems for different cases
图10 中一维平均马赫数、静温、静压沿程分布反映了冷态流场参数的整体趋势,可见平均马赫数从入口处逐渐下降,直到降至燃烧室出口处达到最小值(3.3),在扩张喷管内不断增加至出口处的4.18,而平均静温趋势相反,从入口开始逐渐升高至1789 K,从喷管开始下降至出口处的1284 K,反射波系的存在使得平均静压有一定的波动,压力峰值在注油位下游的激波交汇处,静压沿燃烧室流向小幅增加.

图10 不同状态下一维质量平均马赫数/静温/静压Fig.101 D mass averaged Mach number and static pressure and temperature for different cases
区别于双模态超燃冲压发动机燃烧的强弱可以改变原有波系,形成激波串等新的流动结构[18],对于工作在Ma12 的高马赫数发动机而言,燃料注入并点火后,尽管化学反应带来的热释放会引起波系及流动参数变化,但并未改变激波与膨胀波系贯穿流道的基本结构.当量比0.5 时,激波角相较冷态时明显增大,反射激波数量增多,燃烧室及尾喷管段马赫数明显下降.等直燃烧室出口处,平均马赫数达到最小值2.5,平均静压与静温增至最大值,分别为68 kPa及2630 K.
当量比1.0 时,激波角进一步增大,激波在上下壁面间反射次数增多,燃烧室内马赫数进一步下降,温度整体提升,平均马赫数最小为2.3,平均静温最高为2730 K,均位于燃烧室出口(x=2.435 m)处,但平均静压峰值前移至x=2 m 处,为82.15 kPa.对比平均静温曲线,可知在燃烧室前半段当量比0.5 的平均静温略高于当量比1.0,燃烧室后半段(x> 1.76)当量比1.0 才展现出更高的温升.
2.4 高马赫数发动机燃烧性能分析
为便于对不同当量比下高马赫数发动机燃烧特性有更综合直观的认识,图11 中给出了当量比0.5 与1.0 条件下4 种组分(OH,H2O,O 及H)的一维质量加权平均质量分数的分布曲线.

图11 不同状态下OH/H2O/O/H 一维质量平均质量分数Fig.111 D mass averaged mass fraction of OH/H2O/O/H for different cases
OH 质量分数的分布规律与上文中一维平均静温一致,当量比0.5 时燃烧室前半段OH 更多,燃烧室后半段OH 变化较小,直到喷管处OH 不断下降,而当量比1.0 时OH 从注油位后不断攀升直至燃烧室出口/尾喷管入口处.如果说OH 的分布反映了点火与燃烧,那完全产物H2O 则反映了H2与O2反应是否充分完成,燃料热值能否完全释放出来.H2O 的分布并非单调递增,当量比0.5 时在燃烧室中后段(x=1.88 m) H2O 的质量分数达到峰值后在燃烧室尾部略微降低,直到尾喷管中又小幅度增大.当量比1.0 时这种变化更明显,H2O 质量分数一直增长到燃烧室后部(x=2 m)处,开始明显下降,直至尾喷管中回升.分析H2O 质量分数的下降主要与燃烧室后部的静温水平有关,平均静温高达2730 K,局部静温更高,高温使得H2O 更易离解.
当量比的增加更明显地体现在H 原子质量分数的差异之上,高当量比时H 原子整体更多.而分析O 原子沿程分布规律,可见与当量比1.0 时O 原子在整个燃烧室内逐渐增多相比,当量比0.5 时O 原子生成主要发生在燃烧室前半段,生成速率更快.两种状态下,O 原子复合均主要发生在尾喷管内,O 质量分数明显减小且幅度相当.
图12 中进一步给出了不同当量比下三维燃烧流场中静温、OH 以及H2O 的分布,当量比0.5 时,燃烧室前段温升更明显且均匀,OH 也更多,H2O 的生成主要发生在前段,可见贫油状态下,燃烧距离相对较短,大部分反应在燃烧室前段完成.而当量比1.0 时,燃烧室前段温升与贫油时相比相对略低,温升与OH 生成反映了燃烧反应在燃烧室后段一直持续,燃烧距离较长.

图12 不同状态下流场中静温、OH 及H2O 分布Fig.12 Distribution of static temperature,OH and H2O in flow field for different cases
为进一步增加对燃烧及火焰结构的理解,引入火焰指数GFO[30]定义如下

式中,YO为氧气质量分数,YF为燃料质量分数,GFO可以区分预混火焰及扩散火焰(非预混),GFO为正时代表此处为预混火焰,GFO为负时则为扩散火焰(非预混).
从图13 中当量比0.5 及1.0 状态下流场中火焰指数分布可知,两种情形下流场中绝大部分的燃烧均属于非预混燃烧,火焰为扩散火焰.仅在注油装置hypermixer 沿流向不远处有少部分预混燃烧区域,且预混火焰的位置恰好在注油孔位置的下游.与当量比0.5 时相比,当量比1.0 时更充分的燃料使得预混燃烧区域相对更多.对燃烧形式的认识可以为下一步高马赫数发动机数值模拟中模型的选取与进一步优化提供参考.
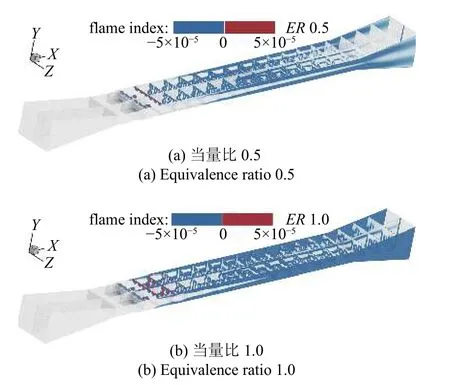
图13 不同状态下流场中火焰指数分布Fig.13 Flame index distribution in flow field for different cases
燃烧反应永远伴随着能量的转化,对于绝热系统而言,化学反应前后系统总焓值恒定不变,总焓由生成焓与总显焓(静显焓与动能之和)组成.燃烧是将燃料的生成焓转化为总显焓的过程.燃烧系统的很大部分能量在化学反应之前都以燃料生成焓的形式存在,化学反应使分子重组.燃烧改变了系统的组分,使反应物向生成物转化.产物的生成焓小于反应物的生成焓,所减少的生成焓提升了系统的总显焓.因此对于绝热系统而言,增加的总显焓等于减小的生成焓(燃烧释热),总显焓增量此时就是燃烧释热量.能量的改变和转移表现为燃烧释热,引起了温度和压力的增加,改变了发动机的流动速度.
针对本文研究的等温壁燃烧系统,化学反应前后系统总焓不再恒定不变,总焓减小量等于壁面传走热量,此时总显焓变化量等于减小的生成焓(即燃烧释热)减去壁面传走热量.冷态时燃烧释热为零,总显焓减小量等于壁面传走的热量,本文称为“壁面热损失”.热态时总显焓变化量等于燃烧释热减去壁面传走的热量,本文称为流道内可利用的“有效释热”.其中总显焓通过以下公式计算

上式中积分沿流向的每个截面进行,ci指的是第i个组分的浓度,Hi(T)与Hi(298.0) 分别指的是温度为T与298.0 K 时第i个组分的静焓,|V|2/2 是气流的动能.V为计算单元表面的流动速度,ds为表面微元的面积向量.
将释热量Hrx对x进行求导,可获得沿流向的释热率HRx,如下式所示

计算得到不同状态下发动机有效释热量与释热率沿流向分布如图14 所示.可见冷态时发动机壁面热损失沿流向基本呈线性分布,壁面传热带来均匀的热损失.

图14 不同状态下燃烧有效释热量及释热变化率分布Fig.14 Distribution of effective heat release and heat rate for different cases
当量比0.5 与1.0 时,注油位后,燃烧释热开始增加,经过一小段距离的累计后可以抵消壁面热损失,随后有效释热量沿流向逐渐增大至燃烧室后部又开始减小,可见燃烧室后部氢燃烧效果较差.该区域静温明显超过Kutschenreuter[31]提出的2500 K 界限,即静温超过2500 K 时,H2与O2反应可获得的净燃烧释热开始迅速减少,性能显著下降.与尾喷管中O 原子复合,完全产物H2O 质量分数增加相符,尾喷管有效释热略有提升.当量比0.5 与1.0 状态下,沿流向释热率均出现波动的情形,释热率较高的波峰处与流场中激波交汇位置较为吻合,可见激波交汇带来的温升与压升有利于燃烧释热.
将燃烧释热(有效释热与壁面传走热量之和)用氢燃料热值无量纲化得到发动机燃烧效率(热值转化率)曲线如图15 所示.可见当量比0.5 时燃料少,更利于掺混,燃烧效率高,发动机出口处约为90%,当量比1.0 时发动机出口燃烧效率约为60%.且根据燃烧释热计算的燃烧效率在燃烧室后部也出现减小的情况,这与H2O 离解吸热相符.

图15 不同状态下燃烧效率分布Fig.15 Distribution of combustion efficiency for different cases
在分析发动机性能时,壁面传热导致的能量损失是不可忽略的一部分,影响着燃烧热的利用率,图16以当量比1.0 状态为例给出了无量纲壁面热流分布(以进气道入口段壁面热流无量纲),反映了壁面热流的相对变化量.图中同时给出了对称面波系分布,可见激波与壁面交汇区域壁面热流明显升高,且随着反射激波沿流向减弱,所带来的壁面热流升高逐渐减少,激波在流道中央交汇的位置壁面热流则相对略小.高马赫数发动机内激波与反射波系常贯穿于流道中,发动机总体设计中必须考虑激波与壁面交汇带来的高热流区域.

图16 当量比1.0 状态下无量纲壁面热流分布Fig.16 Nondimensional wall heat flux distribution for equivalence ratio 1.0 case
最后,分析计算所得M12-02 发动机各部件的推阻力情形,采用动压与面积的乘积对推力进行无量纲,得到推力系数

其中 ρ∞为来流密度,u∞为来流速度,A为进气道入口的横截面积.以同样的方式对摩阻进行无量纲,给出各分部件摩阻系数CFD.计算所得整机及各分部件推力系数与摩阻系数如表1 所示.

表1 M12-02 发动机不同部件推力系数及摩阻系数Table 1 Thrust and friction coefficients of different components for M12-02 scramjet
可见不同状态下燃烧室均为阻力部件,燃烧与冷态相比燃烧室阻力变小,但当量比从0.5 提升至1.0 燃烧室阻力变化较小,总推力系数的差异主要由尾喷管贡献.不同状态下进气道摩阻基本不变,尾喷管摩阻差异较小,燃烧会导致燃烧室摩阻及整机总摩阻减小.
3 结论
针对飞行Ma12 条件下M12-02 超燃冲压发动机开展计算方法的改进以及多状态下精细三维数值模拟,分析发动机内激波与膨胀波波系、参数分布以及燃烧性能特征.结果表明:
(1) 基于AHL3D 软件,对计算方法完成了基于wilcox2006 模型的可压缩性修正.修正后的方法计算所得激波位置及强度与M12-02 发动机试验值吻合良好,在激波串模拟、高马赫数发动机模拟上均展现了更优的能力.
(2) 区别于双模态发动机燃烧的强弱可以改变原有波系并形成激波串等新的流动结构,该高马赫数发动机内形成贯穿流道的激波与反射波系,燃烧热释放并未改变波系贯穿流道的基本结构,且随着当量比增加,激波角增大,反射激波数量增多.
(3) 当量比0.5 时,燃烧室前半段温升、OH 及O 原子质量分数比当量比1.0 时更高,燃烧反应主要发生在燃烧室前部;当量比1.0 时,OH 与静温在整个燃烧室内沿流向不断升高,反应距离更长.O 原子复合主要发生在扩张喷管中.
(4) 流场中绝大部分的燃烧均属于非预混燃烧,火焰为扩散火焰,可为下一步高马赫数发动机数值模拟中模型的选取与进一步优化提供参考.
(5) 燃烧室后段平均静温超过2500 K,完全产物H2O 减少,H2与O2燃烧效果变差.发动机可利用的有效释热在燃烧室前段增加,在燃烧室后段减小.当量比0.5 与1.0 下燃烧室阻力差值较小,总推力系数差异主要由尾喷管贡献.不同状态下进气道摩阻基本不变,尾喷管摩阻差异较小,燃烧会导致燃烧室摩阻及整机总摩阻减小.
(6) 激波与壁面交汇区域壁面热流明显升高,且随着反射激波沿流向减弱,所带来的壁面热流升高逐渐减少,发动机总体设计中必须考虑激波带来高热流区域的影响.
