压气机流动稳定性自适应控制方法研究进展1)
2022-04-07许登科徐瑞泽孙大坤孙晓峰
许登科 董 旭 †, 徐瑞泽 李 佳 孙大坤,, 孙晓峰
* (北京航空航天大学能源与动力工程学院,北京 100191)
† (北京航空航天大学航空发动机研究院,北京 100191)
** (北京航空航天大学杭州创新研究院,杭州 310023)
引言
航空发动机追求更高性能的趋势使得压气机的负荷水平不断提高,从而面临更加严峻的流动稳定性问题.未来智能航空发动机[1]的搭建更是对压气机流动稳定性的自适应控制提出了更为严苛的要求.为了实现这种智能控制,必须首先回答3 个关键问题:压气机的失稳边界如何预测?如何发展流动失稳控制策略和设计方法?如何实现压气机流动稳定性在线监测和系统辨识?从20 世纪50 年代开始,各国学者围绕这3 个问题进行了大量的研究并取得了一系列成果.然而,截止目前的研究工作对于回答这3 个问题仍然有一定距离.
压气机的失稳边界如何预测一直以来都是难点和焦点.目前的压气机设计仍然基于Wu[2-3]在20 世纪50 年代提出的两类流面理论.压气机的稳定裕度一方面通过在二维通流设计阶段选取合适的经验参数来保证,另一方面在三维造型完成后通过定常数值模拟进行校核.其中,经验参数的选取标准来源于不断积累的大量实验数据和设计师自己的设计经验,这些很难满足当代先进压气机的设计需求.定常数值模拟只考虑非定常流动的时均效果.在压气机失速起始尚未形成明显失速团的时候,这种流场变化会被时均效应抹掉从而仍然得到流场收敛解.因此,定常数值模拟往往会对压气机的稳定裕度做出乐观的评估,这也就为压气机的实际稳定裕度是否达到要求埋下了隐患.设计定型的压气机进行试车实验时一旦发现稳定裕度不足,要么采取扩稳措施进行补救,要么重新设计.而补救措施的能力往往是有限的,一旦需要重新设计将会损失惨重.新一轮的设计方案仍然没有可靠的评估工具在设计阶段就进行稳定裕度的校核,那么试车结果的不确定性是可想而知的.因此,为压气机设计阶段发展可靠的流动稳定性预测工具是工程上的迫切需求.
当压气机稳定裕度不足时如何发展可靠的扩稳措施增加稳定裕度也是实现稳定性自适应控制的关键环节.在失速发生之前就会出现的周向扰动波的发现使得研究人员对于失速演化过程有了突破性的认识和理解.这一发现首先是由Moore和Greitzer[4]于1986 年合作提出的M-G 模型在理论上预测得到的.M-G 模型是可以包含周向扰动的非线性模型,捕捉到了具有周向分布特征的周向大尺度失速先兆波.这一大尺度先兆波,也就是模态型扰动波[5-6],很快由Mcdougall 等[7]率先在单级低速大轮毂比的压气机实验中发现.随后Garnier 等[8]也在实验中测到了周向模态型扰动波的演化过程.这一失速先兆波的发现为各国学者发展扩稳措施提供了新思路.基于“反声原理”的主动控制技术[9-10]开始出现,这一技术的扩稳思路是通过激励器产生与失速先兆波幅值相等相位相反的扰动波来对消失速先兆波从而阻止失速.然而,激励器的带宽、全周传感器的昂贵费用、大规模数据处理系统以及激励器本身对于其进一步应用到工程上的真实压气机中都是巨大的挑战.最致命的是1993 年Day[11]在实验中发现了不同于模态型扰动波的另一种周向小尺度失速先兆波,被称为Spike 型失速先兆波[12-13].这种先兆波的周向尺度与叶片通道尺寸相当,而且一旦出现这种扰动,压气机很快就会失速.即使主动控制技术的传感器在周向布置得足够密以至于能够捕捉到这种尺度的失速先兆波,也没有足够的时间留给激励器去产生与之对消的扰动波.因此,基于“反声原理”的主动扩稳控制技术在具体实施过程中阻力重重.
另一方面,以机匣处理为代表的被动控制技术在压气机扩稳方面取得了很好的效果.从Koch[14]在一台单级轴流压气机上偶然发现机匣处理在实验中取得扩稳效果开始,截止当前机匣处理已经有50 多年的发展历史了.机匣处理由于其结构简单、可靠性高以及抗进气畸变能力强[15]已经被广泛应用于工程中.传统机匣处理结构多样[16-18],有带背腔的穿孔板、轴向缝或槽、周向槽、斜槽以及蜂窝结构等,但不同结构的扩稳效果差异明显.即使结构相同,但开孔率、缝或槽深、腔深等几何参数稍有改变也会引起扩稳能力的显著变化.传统机匣处理由于其特殊结构对叶尖间隙流动和主流流场的干扰过大,不可避免地会带来压气机总体性能变化尤其是效率下降、通用性差等一系列问题.究其原因,主要在于缺乏对于机匣处理结构参数的理论设计准则.目前研究人员对于传统机匣处理的设计仍然是基于经验和试错的方法.正如Smith和Cumpsty[19]所说,人们对于机匣处理产生扩稳效果的原因仍然没有很好的理解.那么,如何建立相应的理论设计准则并基于此发展可靠的扩稳措施是亟待解决的关键问题.
为了不影响设计定型的压气机本身的气动性能,当其工作在靠近失速边界时是实施扩稳措施的最佳时机.因此,在发动机运行阶段如何在线实时监测稳定性从而为扩稳措施提供可靠的触发信号是实现自适应控制的关键一步,这也就是失速预警技术.传统预警方法各种各样,主要基于小波分析[20]、傅里叶分析[21]以及方差分析[22]等信号处理技术,但其最大的局限性在于预警时间不足以支持作动机构执行扩稳措施.因此,发展新的失速预警技术将预警时间大大提前才有可能实现稳定性控制,这也是构建自适应扩稳控制方法必须克服的困难.
综上所述,只有在上述提到的3 个关键问题上有所突破,才能搭建起压气机流动稳定性的自适应控制系统.因此,本文主要围绕风扇/压气机全局稳定性理论预测模型方法、基于壁面阻抗调控的扩稳方法和基于气动声学原理的失速预警方法3 方面的发展历史与最新进展进行概述,并最终阐述如何利用这3 个关键技术构建面向未来智能航空发动机的流动稳定性自适应控制方法.
1 流动稳定性预测
1.1 理论模型的发展
在当前压气机设计体系中,D因子[23]作为与稳定性相关的特征参数仍然发挥着不可替代的作用.根据实验得到的D因子和损失参数的关联曲线可以建立熵增与损失系数之间的关系.D因子反映了压气机叶片吸力面减速扩压段的逆压梯度,从而表征了吸力面附面层分离的难易程度.D因子大于临界值,则吸力面附面层容易分离,这也就为形成旋转失速团提供了条件.其本质上是一个二维局部参数,仅能刻画展向各个基元叶型各自的流动情况.而旋转失速是一个全局稳定性问题,并不能由局部流动情况来表示.另外,压气机叶片通道局部的流动分离与旋转失速之间的关系尚不清楚.因此,在压气机设计过程中仅通过D因子等经验方法来保证稳定裕度存在着很大的不确定性,发展流动稳定性预测工具成为了工程上的迫切需求.
压气机流动稳定性理论模型从1955 年的Emmons 模型[24]开始至今已经发展了60 余年.Emmons模型基于线性稳定性分析的思想将压气机内的流动稳定性问题转化为研究背景流场对任意小扰动的响应,如果所有小扰动都随时间衰减最终系统恢复原来的状态那么判定当前系统是稳定的.Emmons 模型通过假设背景流二维定常无黏不可压,扰动场无旋,将扰动速度势满足的Laplace 方程作为扰动场的主控方程,其本质上是一个线性常微分方程.根据线性系统的特征值理论,可以通过特征值的正负号来确定小扰动的演化趋势,从而判断压气机系统的稳定性.Emmons 等[24]认为叶片通道堵塞是旋转失速发生的重要原因,因此提出了一个表示叶片通道出口有效流通面积的参数,并假设其为进口气流角的函数,并由此推导出了一个失速起始的判据,即叶片通道出口有效流通面积关于进口气流角正切值的导数一旦超过临界值,压气机内的流场就会变得不稳定.该模型中应用的线性稳定性分析和特征值理论对后续线性模型的发展提供了重要参考.
著名的M-G 模型[4]是由Moore和Greitzer 合作提出的.该模型假设流动二维不可压,并定义B参数作为压气机流动稳定性的判据.该模型可以预测失速起始以及失速后系统的非线性演化过程,为失速先兆波的发现和主动扩稳控制方法的发展提供了理论指导.随后,Hynes和Greitzer[25]将M-G 模型线性化,并利用线化模型研究了进气畸变对多级压气机流动稳定性的影响.
上述模型均基于不可压假设,而实际大多数压气机中流动压缩性是不可忽略的.因此,为了考虑流动的压缩性,Bonnaure[26]首次提出了二维可压缩失速起始预测模型,可以包含涡波和熵波的影响.高负荷压气机内部流动尤其是畸变进气条件下具有强烈的三维非均匀性.为考虑这一点,Sun[27]基于无穷维系统的截断技术和有限空间波传播界面间的模态匹配方法从线化Euler 方程出发,综合考虑3 种小扰动波(即涡波、熵波和压力波),推导出了可以考虑任意阶径向扰动的三维可压缩失速起始预测模型.在此基础上,于巍巍等[28]和Sun 等[29]基于等价分布源法和传递单元方法将机匣处理视为壁面阻抗边界条件加入模型中,并在半激盘模型中成功引入激波匹配条件,使得模型适用于跨音压气机并能考虑机匣处理对稳定性的影响.以该模型作为理论指导,Sun等[30-31]设计了一系列机匣处理方案并开展了大量的实验验证工作.
虽然上述理论模型在揭示旋转失速背后的物理过程方面发挥了重要价值,但其对压气机几何结构和流动细节均进行了大幅简化.将叶片排简化为激盘或者半激盘,通过分段平均的方式忽略流动的不均匀性,这些都限制了模型预测的精度.因此,为了能够准确评估压气机的失速起始流量点,对于现代先进压气机而言,必须采用既能考虑压气机具体几何形状,又能考虑流场细节的方法.
除了发展理论模型来进行压气机流动稳定性预测外,非定常数值模拟[32-34]也是一条思路.该方法将压气机的流动失稳作为初边值问题来求解,本质上是一个数值模型.该方法利用贴体网格的方法将压气机几何结构考虑在内,并能包含丰富的流动细节,不仅可以求得压气机的失稳流量点,而且可以直接得到失速之后的演化过程,因此对于揭示流动失稳背后的物理机理具有重要意义.但限于目前的计算能力,考虑到计算资源和计算时间,工程上应用更广泛的是三维可压缩黏性定常数值模拟.非定常数值模拟在湍流模型的选取、边界条件的设定、是否需要引入以及如何引入初始扰动等方面仍存在很多问题.除此之外,这种方法对于计算资源和计算时间的巨大消耗也是限制其工程应用的重要原因.
为了克服上述理论模型与非定常数值模拟各自在预测压气机失稳点方面的不足,并试图为压气机设计阶段发展能够快速可靠评估稳定性的工具,Sun 等[35]在2013 年提出了叶轮机械流动稳定性通用理论.该方法基于线性全局稳定性分析和浸入式边界方法的思想,综合了解析模型和非定常数值模拟的优势,既能考虑叶片几何和流动细节,又有可观的计算效率.通用理论借鉴了解析模型中的线性稳定性分析思路,将压气机失速起始点的预测归结为特征值问题求解,并利用特征值虚部正负作为压气机是否失稳的判据.同时,又借鉴了基于叶片力模型考虑叶片几何影响的数值模拟方法[36],将具体的叶片几何模化为体积力源项加入到主控方程中,从而避免了生成贴体网格的困难,在考虑叶片几何形状的同时大大降低了计算量.由于该方法分析的背景流场是由三维黏性定常数值模拟得到的,因此可以将三维流动非均匀性考虑在内,是一种全局稳定性分析方法.
1.2 流动稳定性通用理论
1.2.1 通用理论架构
本节首先简要介绍叶轮机流动稳定性通用理论的建模过程,具体的公式推导不再赘述,见文献[35].基于浸入式边界思想,叶片几何可以由分布式体积力源项代替.因此,压气机内部流动可以由带力源项的Navier-Stokes 方程来描述,质量守恒、动量守恒以及能量守恒方程就可以写为

式中,f为单位流量的叶片力矢量,u为速度矢量.Π为包含正应力和切应力的二阶应力张量,其表达式为,μ 为黏性系数,I为3 阶单位阵.e为内能.在理想气体假设下,流体满足状态方程p=ρRgT,从而e=cvT=
基于小扰动理论,流动参数的瞬态量q可以写成定常量与非定常小扰动量q′之和,即

式中,q代表物理参数 ρ,u,p以及f.
叶片力源项的作用在于反映叶片几何对流场的影响,因而可以写成当地流动参数的函数,即f=f(ρ,u,v,w,p).根据一阶泰勒展开,可以得到力源项的扰动量

将式(2),式(3)代入式(1),减去定常背景流满足的零阶方程,忽略高阶小量,则可得到关于扰动量的线化控制方程.
考虑到定常背景流的三维非均匀性,将扰动量进行时间傅里叶展开

式中,为扰动量幅值,ω 为复数特征频率.
将式(4)代入线化控制方程进行整理,最终可以写成矩阵形式

式中,A,B,C,E,G,H,M,N,Q,R为系数矩阵,F为与叶片力源项相关的矩阵,这些矩阵中的元素为定常背景流物理量及其空间导数的组合,因此仅与所分析的定常流场有关.为扰动量幅值组成的列向量.可以看出,式(5)中左边项的变量只有复数特征频率 ω.将左边项整体记为L(ω),则式(5)可以写为


通过求解式(7)可以得到系统特征值ω=ωr+iωi.由式(4)可以看出,特征值虚部代表了扰动量随时间的演化趋势:虚部大于零,扰动量随时间增长,系统不稳定;虚部小于零,扰动量随时间衰减,系统稳定.特征值实部表示失速起始扰动波的周向传播速度,大量研究表明,该速度与转子转动速度在同一量级.因此,利用转子转速对特征值实部和虚部分别进行无量纲化从而得到两个无量纲参数RS(relative speed,相对速度)和DF(damping factor,衰减因子),他们的表达式为

式中,Ω 为转子转速,单位为rad/s.
对于特殊几何的叶轮机械,通过补充合适的边界条件、转静交界面上的匹配条件和叶片力模型即可最终完成流动稳定性通用理论的建立.
1.2.2 简化模型
为了适应压气机设计阶段不同层次的需求,在保证预测精度的情况下节省计算资源和时间,孙晓峰等基于通用理论发展了相应的降阶稳定性模型,目前有子午面模型[37-39]、流线模型[40]和径向展开模型[41],并通过大量算例校核了这些模型预测压气机失速起始点的精度以及用于稳定性分析的价值.下面展开介绍这些简化模型.
(1) 子午面模型
在均匀进气或者径向畸变进气条件下,压气机内部流场的周向不均匀性并不显著,也就是三维流场信息基本可以由子午流面上的流场信息反映.因此,基于轴对称假设,忽略背景流的周向不均匀性,将子午流场作为通用理论稳定性分析的背景流场是合理的降阶方式.这种降维方式在工程中非常普遍,压气机通流设计中基于轴对称假设、周向均匀假设或者中心流面法的降维处理目前仍广泛应用.另外,考虑到压气机内部流动雷诺数通常很大,黏性对流动稳定性的影响有限,子午面模型在扰动方程中忽略黏性相关项,而将黏性损失包含在了叶片力模型中.事实上由黏性数值模拟得到的背景流场中已经包含了黏性的作用.除此之外,基于绝热假设在能量方程中忽略热传导和热生成,最终构建子午面稳定性模型.
由于假设背景流周向均匀,扰动量的周向模态解耦,故扰动量可以作周向傅里叶展开,即

式中,mc为扰动量的周向波数.忽略线化控制方程中背景流的周向偏导数项、黏性项以及热相关项并将式(9)代入整理,得到

式(10)即为子午面模型最终需要求解的特征值方程.
(2) 流线模型
为了进一步减小计算量,分析压气机内部流动稳定性的展向分布情况,在子午面模型的基础上以子午面上单条流线的信息作为背景流进行稳定性分析从而评估各流线的流动稳定性情况,这就是流线模型.该模型能够定量评估压气机各展向位置的流动情况,从而辨识流动稳定性的薄弱位置,这对于工程中压气机设计阶段的三维叶型设计具有指导意义.
流线坐标系 (n,θ,s) 如图1 所示.将子午面模型的控制方程在流线坐标系下展开,忽略法向动量方程,则最终可以得到流线模型的特征值方程,即


图1 流线坐标系Fig.1 Streamline coordinate system
(3) 径向展开模型
对于大轮毂比、流道收缩不明显的压气机,其内部流动在展向近似均匀.因此,在子午面模型的基础上忽略背景流的径向不均匀性,即可得到径向展开模型.这一模型对离心压气机的失稳点预测展示出了很大的潜力.
由于假设背景流在周向和径向都是均匀的,因此扰动量在周向和径向均可以作傅里叶展开,即

式中,nr为扰动量的径向波数.忽略子午面模型方程中的背景流径向偏导数项,并利用式(12)代入方程式(9),即可整理得到径向展开模型的特征值方程
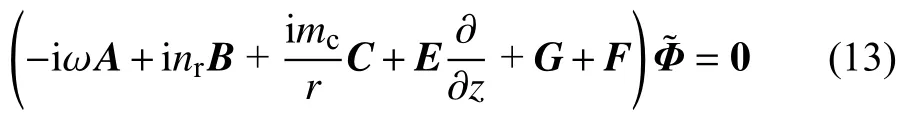
1.2.3 模型验证
为了校验所发展的理论模型的预测精度及应用价值,针对不同跨声速、亚声速轴流压气机以及离心压气机的流动失稳点预测工作陆续开展,转子叶顶气流相对马赫数范围从0.25~ 1.50.大量的验证结果表明,子午面模型对于轴流压气机失速起始点预测的相对误差在3%以内[37-39],径向展开模型对于离心压气机失稳流量点预测的相对误差在5%以内[41],流线模型能够捕捉压气机展向各流线流动稳定性随节流过程的变化并能识别流动稳定性的径向薄弱位置[40].
图2 展示了利用子午面模型预测得到的跨声速压气机NASA Stage35 的失稳流量为18.26 kg/s.与实验中测得的失稳流量(约为18.20 kg/s)相比,相对误差仅为0.33%.图3 展示了利用径向展开模型预测得到的NASA 低速离心压气机的失速起始流量为15.6 kg/s.与实验中测得的15.0 kg/s 相比,相对误差为4%.NASA Rotor37 展向31 条流线的流动稳定性随节流过程的变化在图4 中给出,这是流线模型预测的结果.其中,从叶根到叶尖流线序号依次为1~ 31.可以看出,随着节流过程的进行,靠近叶尖部分的流线流动稳定性逐渐恶化,而靠近叶根区域的流线稳定性基本不变,从而判定叶尖为流动稳定性的薄弱位置.

图2 NASA Stage35 子午面模型预测结果[38]Fig.2 Prediction result of NASA Stage35 via meridian surface model[38]
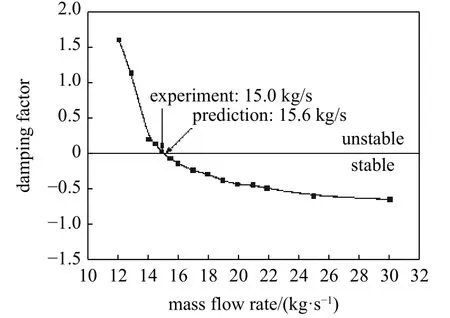
图3 NASA 低速离心压气机径向展开模型预测结果[41]Fig.3 Prediction result of NASA low-speed centrifugal compressor via radial expansion model[41]

图4 NASA Rotor37 流线模型预测结果[40]Fig.4 Prediction result of NASA Rotor37 via streamline model[40]
1.2.4 模型应用
三维叶片弯掠设计技术由于其在提高压气机性能和拓宽稳定裕度方面的巨大潜力已经被广泛应用于现代先进压气机中,但叶片掠对于压气机稳定性的影响一直没有定论.由于通用理论有能力刻画叶片三维叶片几何的影响,因此基于通用理论在揭示掠叶片影响压气机稳定性的机制方面进行了探索式研究[38-39].图5 给出了利用子午面模型研究的叶尖弦向后掠对NASA Rotor37(R37)流动稳定性的影响规律.可以看出,叶尖弦向后掠会使压气机的失速起始流量点提前,也就是会恶化压气机的流动稳定性.

图5 叶片后掠对NASA Rotor37 流动稳定性的影响[39]Fig.5 Effect of backward swept blades on flow stability of NASA Rotor37[39]
2 扩稳方法研究
如引言中所述,在利用模型方法、数值方法以及实验方法获得设计定型的风扇/压气机的失稳边界后一旦发现当前设计无法提供充足的稳定裕度,为了不改变已有设计,就必须要采用各种各样的扩稳措施以弥补稳定性设计上的不足.其中,机匣处理在目前工程上的压气机扩稳措施中占据主导地位.传统机匣处理结构多样,在压气机扩稳方面展示出了很好的效果.但由于没有理论设计准则,其通用性差,在一台压气机上有扩稳效果的机匣处理往往并不适用于另一台压气机.另一方面,正如Fujita和Takata[42]所强调,效率损失是机匣处理的最大缺陷.Fujita 等对不同类型和同一类型不同几何的机匣处理进行了研究和总结,如图6 所示.可以看出,对传统机匣处理而言,其在带来稳定裕度提升的同时会引起峰值效率的下降.那么如何使机匣处理设计有章可循?是否可以做到在扩稳的同时保持压气机的峰值效率和压比特性?
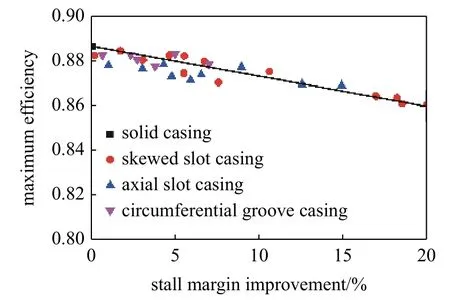
图6 不同机匣处理下的转子最大效率与失速裕度提升[42]Fig.6 Relation between rotor maximum efficiency and stall margin improvement[42]
2.1 失速先兆抑制型(stall precursor-suppressed,SPS)机匣处理
2.1.1 扩稳机理
失速先兆的发现为压气机扩稳控制带来了新的启示,主动控制扩稳技术通过引入具有相同幅值且相位相反的人为扰动来对消失速先兆,取得可观的扩稳效果.振奋的同时,也应该看到,这种采用精准对消的方式,在具体实施方面面临着巨大的挑战:第一,如何准确识别失速先兆?越来越多的研究表明,压气机系统存在各种各样的失速扰动,同一台压气机在不同的进气条件下可能存在不同的失速行为,同一种失速先兆(例如spike),在同一台压气机可能起始于不同的位置.第二,作动机构是否及时?任何机构的启动、工作、产生效果,都需要一定的时间,而失速先兆从发现到压气机失速往往只在几转的时间,传统机械结构根本来不及.一旦解决这两个问题,主动控制技术一定能够为压气机扩稳控制做出更大的贡献.但是,也更应该认识到,主动控制并不是抑制失速先兆的唯一手段.对于一个动力系统来说,其演化行为受到初始条件和边界条件的影响,那么通过一定的方式引入额外的阻尼同样可以有效地抑制演化中的扰动放大.那么,是否可以通过设计机匣处理结构只抑制失速先兆波的演化而不改变叶尖流场结构来实现扩稳呢?这一问题很快得到了肯定回答,也就是失速先兆抑制型(SPS)机匣处理[30-31]的诞生.需要明确,要对失速先兆进行控制基于传统的定常机匣处理是无法做到的,必须采取非定常的方法.基于Howe[43]提出的涡声理论,非定常边界或阻抗边界可以在封闭环境中与压力波相互作用.那么问题就转化成为如何设计机匣处理来建立这种非定常边界条件.
SPS 机匣处理的结构如图7 所示,由一个环形背腔和带有圆孔或斜槽的穿孔板构成.当压气机工作时,由于叶片两侧压力差的作用,在叶尖部分的气流从斜槽尾缘流进背腔,再从斜槽前缘流出,这种循环流动自然存在.而气流在流过孔板/斜槽时,由于压力扰动的作用会在孔缝边缘激起脱落涡,从而将扰动波的能量转化为涡能,由于黏性的作用涡能进一步的被耗散掉.实际上,SPS 机匣处理扮演了非定常边界的作用,在物理上,可以用阻抗的概念来描述这种边界.已有的研究表明[44],当穿过孔缝的气流速度改变时,不仅可以改变阻抗边界条件,还会影响其吸声效果.Jing 等[45]曾经研究了偏流对背腔穿孔板结构的吸声性能的影响,结果表明,不论偏流是流入孔缝还是流出孔缝,只要偏流流速相等,造成的是同样的阻抗边界.这就是SPS 机匣处理扩稳的基本机理.

图7 SPS 机匣处理波涡相互作用示意图Fig.7 Diagram of wave vortex interaction in SPS casing treatment
2.1.2 理论设计方法
SPS 机匣处理的作用机理为系统的阻抗边界,不仅在机理上有别于改变定常流动结构的传统机匣处理,其在理论设计方法上还具有先天的优势,原因在于SPS 机匣处理结构中的几何参数可以和系统阻抗边界建立起严格的数学物理关系.理论模型的发展部分提到,于巍巍等[28]和Sun 等[29]将机匣处理视为壁面阻抗边界条件建立了可以考虑机匣处理影响的三维可压缩失速起始预测解析模型.要想建立包含SPS 机匣处理的特征值问题,首先要明确SPS 机匣处理所提供的“软”壁面边界条件在理论模型中如何刻画.受气动声学启发,将SPS 机匣处理作为阻抗边界条件加入到模型中是一条思路.那么这种阻抗边界条件在稳定性模型中如何描述依然非常棘手.这是因为,穿孔板处的法向质点位移连续条件中涉及到径向特征值的求解.需要指出,在带有声衬的管道声学问题中,使用模态匹配方法计算声衬段扰动波的径向特征值也遇到了困难.为规避求解非均匀壁面阻抗条件下的径向特征值问题,1981 年Namba和Fukushige[46]提出了等价分布源方法.该方法将声衬壁面视为刚壁与若干未知强度的单极子声源的叠加,把原本复杂的声场转化为刚壁条件下的声场与壁面单极子源产生的声场的叠加,将问题转化为建立壁面的阻抗方程并借助于格林函数的方法求解由壁面点源产生的散射场.在该方法的基础上,王晓宇和孙晓峰[47]进一步发展,解决了其中的奇异性问题.借鉴气动声学的发展,最终将SPS 机匣处理借助于等价分布源方法描述成为稳定性模型中的边界条件,并结合传递单元方法和模态匹配完成包含机匣处理的特征值方程的建立,具体推导过程见文献[29].这一模型的建立使得SPS 机匣处理有了理论设计工具,可以有效评估诸如腔深、开孔率、背腔长度等机匣几何参数变化对压气机流动稳定性的影响规律,从而针对特定压气机通过参数化研究可以得到实现其最佳扩稳效果的机匣几何参数.
下面以北航单级亚声速压气机TA36和跨声速压气机J69 为例,展示带机匣处理的失速起始预测模型对于SPS 机匣处理结构参数影响的评估能力.不同结构参数机匣处理扩稳效果的模型预测结果如图8 所示,其中 σ 为穿孔率,hb为背腔深度,lb为背腔长度,Mab为流经穿孔板的偏流马赫数.SW(solid wall)代表光壁机匣,CT(casing treatment)表示机匣处理.从图8 中可以看出,对亚声速压气机TA36 而言,当背腔深度、背腔长度和偏流马赫数为固定值时,穿孔率增大会改善SPS 机匣处理的扩稳效果;对跨声速压气机J69 而言,固定背腔长度、穿孔率和偏流马赫数,增大腔深可以提高SPS 机匣处理的扩稳能力.

图8 不同结构参数SPS 机匣处理扩稳效果理论预测[48]Fig.8 Stability prediction of SPS casing treatment with different structural parameters[48]
2.1.3 扩稳效果实验验证
为了验证SPS 机匣处理的扩稳效果,在亚声速和跨声速压气机上进行了大量的实验研究[31,48-49].这里仅展示其中一部分实验结果来简要说明.在亚声速压气机TA36 上SPS 机匣处理的扩稳实验结果如图9 所示.可以看出,SPS 机匣处理具有显著的扩稳能力,而且并没有带来效率亏损.针对跨声速压气机J69 的扩稳实验结果在图10 中展示.很明显,SPS 机匣处理在60%和96%设计转速下均带来了明显的裕度收益,而且能够保持压气机原有的压升和效率特性.

图9 SPS 机匣处理在亚声速压气机TA36 上的扩稳实验结果[31]Fig.9 Experimental results of SPS casing treatment on subsonic compressor TA36[31]

图10 SPS 机匣处理在跨声速压气机J69 上的扩稳实验结果[49]Fig.10 Experimental results of SPS casing treatment on transonic compressor J69[49]
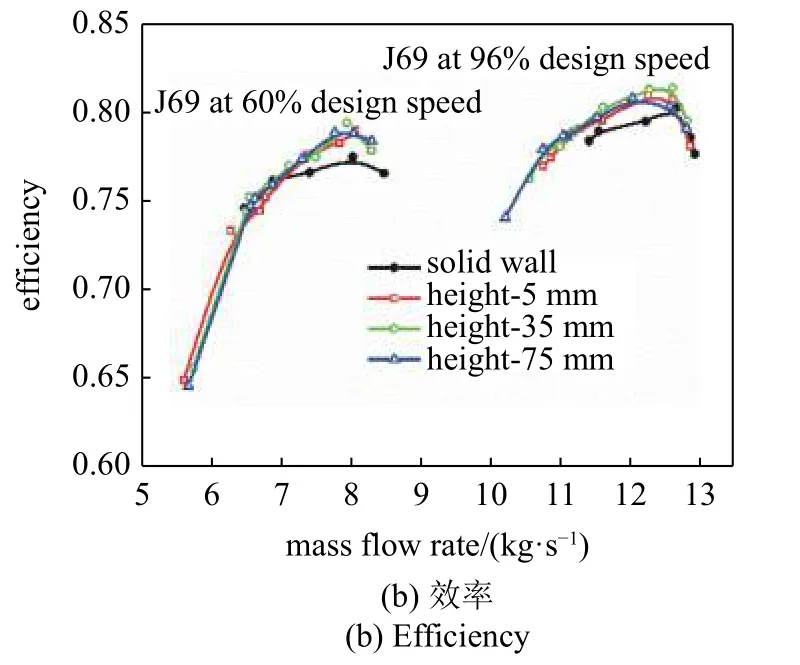
图10 SPS 机匣处理在跨声速压气机J69 上的扩稳实验结果[49](续)Fig.10 Experimental results of SPS casing treatment on transonic compressor J69[49] (continued)
2.2 泡沫金属机匣处理
从系统阻抗边界调控的角度出发,除了利用SPS 机匣处理构建具有阻抗边界特征的措施来抑制失速先兆波外,还可以利用新型材料填充机匣处理结构,以实现扩大稳定工作范围和吸收风扇噪声的双重效果,这对降低结构复杂性和减小部件重量具有重要意义.研究发现,泡沫金属材料是一种具有高孔隙率的泡沫状合金,尽管本身具有多孔结构,但其强度和刚度保持了金属特征,而且质量很轻,符合航空发动机减重的需求.优良的性能使其广泛应用于隔热、减震、降噪等方面.据公开文献显示,Sutliff和Jones[50]首次将泡沫金属材料用于叶轮机械.他们将基于泡沫金属设计的声衬安装在低速和高速风扇的转子叶片上端,并通过一系列实验证实了这种声衬具有优秀的吸声效果;另外,Xu和Mao[51]的研究表明泡沫金属在离心压气机中也有很好的降噪效果.而随着民用大涵道比航空发动机的风扇尺寸不断增大导致短舱重量也随之增加,为了减重的需要,声衬的轴向安装位置越来越靠近风扇转子,甚至二者发生重叠,其相互作用对声衬的降噪特性和风扇的气动特性与稳定性均产生了一定的影响.鉴于这一问题在工程上的迫切性,Sun 等[52]提出了一种泡沫金属机匣处理(foam metal casing treatment,FMCT),将转子段机匣内壁面设计为填充泡沫金属材料的机匣处理结构,实现了压气机扩稳和降噪的双重收益,并通过理论分析与实验测量研究了泡沫金属机匣处理与风扇的相互作用规律和扩稳降噪机理.
北航流体与声学工程实验室在其单级亚声速轴流压气机TA36 实验台上进行了大量实验研究以探究泡沫金属机匣处理的扩稳降噪能力[52-53].泡沫金属可以由PPI (pores per inch)也就是每英寸气孔数来表示其材料特性.PPI 越大说明泡沫金属的单位气孔数越多.实验中选取了20,35和50 这3 种PPI 的泡沫金属机匣进行了尝试.图11 给出了实验中泡沫金属机匣处理相对于转子叶尖的两种安装位置.其中,L1 CT 表示泡沫金属机匣处理安装在图中的①位置,L2 CT 表示在图中的②位置处安装泡沫金属机匣处理.为方便起见,光壁机匣记为SW,L1 CT20 表示PPI 为20 的泡沫金属机匣安装在①位置,同理可得其他表示.

图11 泡沫金属机匣处理在实验中的安装Fig.11 Installation of foam metal casing treatment in experiment
图12(a)比较了实验测得的光壁条件和L1 CT壁面条件下的TA36 的压升特性曲线.可以看出,L1 CT 机匣并没有明显改变压气机原有的压升特性.3 种PPI 的L1 CT 机匣和光壁机匣下实验测得的带误差限的失稳流量点展示在图12(a)左下角的小方框中.可以看到,这3 种L1 CT 机匣都取得了一定的扩稳效果,大约有5.4%~ 8.7%的综合裕度提升.通过比较图12(b)中不同机匣下压气机的效率特性可以发现,这3 种PPI 的L1 CT 机匣在设计点都没有明显改变压气机的效率特性.

图12 带L1 CT 的压气机特性线[52]Fig.12 Compressor characteristics with L1 CT[52]
带L2 CT 机匣的压升特性和效率特性曲线分别在图13(a)和图13(b)中展示.很明显,与L1 CT 机匣相比,L2 CT 机匣的扩稳效果更加显著,大概有22.2%~ 37.1%的综合裕度提升,但会带来1.1%~2.1%的效率损失.

图13 带L2 CT 的压气机特性线[52]Fig.13 Compressor characteristics with L2 CT[52]
为探究泡沫金属机匣处理的声学效益,通过实验测量比较了L1 CT50和L2 CT50 机匣在设计流量点对压气机噪声的影响,如图14 所示.声压级S PL(sound pressure level)的表达式为

图14 设计工况下L1 CT50,L2 CT50和光壁机匣下压气机的声压级[52]Fig.14 Sound pressure levels of compressors with L1 CT50,L2 CT50 and solid wall casing at design operating condition[52]

式中,psound表示声压,pref=2×10-5Pa 为基准声压.S PL的单位为dB.从图中黑色曲线可以看出光壁条件下TA36 压气机发出的噪声是离散纯音噪声主导的,主频为3 阶BPF (blade-passing frequency,叶片通过频率).在L1 CT50 机匣的作用下,3 阶BPF和4 阶BPF 的噪声分别降低了5.9 dB和6.0 dB.而L2 CT50 机匣使得3 阶BPF和4 阶BPF 的噪声都有略微增加.但总体来看,这两种位置的泡沫金属机匣处理在压气机宽频噪声的抑制上均有明显收益,如图中的虚线方框所示.
由以上结果可以看出,泡沫金属机匣处理在帮助压气机减重的同时,有能力实现扩稳和降噪的双重收益,具有广阔的发展前景.
3 在线实时失速预警方法
第2 节中发展的扩稳执行机构仍需要与可以监测压气机工作状态的实时失速预警技术相结合才能最终实现压气机自适应控制方法.通过在压气机运行时采集数据并进行在线分析,识别压气机工作状态的变化情况并在其失稳前及时发出预警信号,失速预警技术可以让执行机构在不同工况下提供不同程度的控制策略,提高扩稳效率.传统的失速预警技术大多是通过捕捉失速先兆(包括模态型和Spike型扰动波)的方式进行预警,但由于失速先兆波的出现位置随机,且从探测到压气机失速先兆到其非线性演化为失稳的时间间隔仅为0.03~ 1 s[7-8,11],这种方法并不能提供稳定且充足的预警时间.Li 等[54]根据气动声学的原理,将机匣壁面的动态压力信号周期性与压气机不同工况下转子载荷的变化情况联系起来,建立了可以将预警时间提高到秒量级以上的失速预警方法.下面简要介绍该预警方法及实验效果.
3.1 失速预警机制
在压气机系统中,转子叶片产生的压力波会在轮毂和机匣形成的管道中向上游和下游传播,这种压力波的传播可以由广义Lighthill 方程[55]来描述

对方程进行求解,可以得到t时刻位于x位置感受到的各个叶片产生的压力扰动为

对于安装于机匣壁面的传感器(图15),若其位置坐标为 (rc,θ=0,zs),其采集到的压力脉动信号可表示为

图15 压力传感器安装位置示意图Fig.15 Installation position of pressure sensor

式中,Fsm,n,j(zs,k)可以通过以下积分得到

若一台压气机的转速为 Ω,则传感器在某一时刻t0的压力信号与相邻转子周期t0-2π/Ω 时刻的压力信号的差值为

根据库塔-茹科夫斯基升力定理,叶片所受升力等于叶片吸/压力面静压差沿中弧线的积分,即
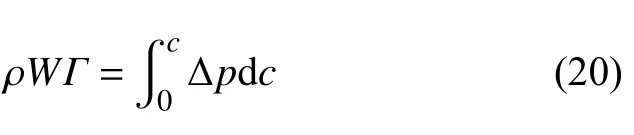
则

这样便建立起了传感器检测的压力信号与叶片环量之间的关系.
当压气机工作点离失稳边界较远时,叶片区流场内的非定常涡脱落非常微弱,因此叶片环量在一个甚至几个转子转动周期并不会发生明显变化,传感器采集到的压力波信号具有较好的时间周期性.而当压气机工作在近失速点时,叶片区流动分离和涡系结构变得十分复杂,流动表现出强烈的非定常性,转子叶片表面剧烈的非定常涡脱落会导致叶片环量在一个或几个转子转动周期内发生明显变化,这也就导致传感器采集到的压力波信号的时间周期性被破坏.随着压气机工况点逼近失速,叶片环量变化从刚开始的某几个叶片和随机发生逐渐变为更多叶片和频繁发生,最终叶片环量减小使得压气机失去原有的增压能力,旋转失速随即发生.因此,可以通过这一机制来进行失速预警.
为了定量评估压力信号的时间周期性,基于相关性分析定义了参数

式中,Rc(j)是Rc在j点的值,j是当前采样点的序号,p为压力信号,N为一个转子周期的采样点数,n为计算窗口内的采样点数.n的取值范围可以从一个叶片通道内的点数到一个转子周期的点数,点数越大意味着计算量越大.从式(15)可以看出,Rc(j) 是通过第j个采样点及其之前采样点的数据得到的,因此随着压力信号的持续采样,Rc随着时间的变化规律可以通过同步计算来获得,这就为在线实时监测的可行性提供了基础.理论上,Rc值越接近1 表示压力信号的周期性越好,越远离1 表明周期性越差.
基于以上理解,在节流过程中通过连续采样得到的Rc值会在接近失速时骤降.如果对Rc设置合理的阈值,越靠近失速边界,就有越多采样点的Rc值小于阈值.为统计这种概率分布,引入累积分布函数

式中,Rcth为Rc的阈值,P(·) 表示概率值.这样一来,越靠近失速边界,Rc降低的幅度越大,其小于阈值的概率就越大,F(Rcth)就越大.对F(Rcth) 设置警戒值,即随节流过程进行当F(Rcth) 增大到警戒值时发出预警信号.这样,在线实时统计F(Rcth) 即可实现失速预警.
3.2 预警方法在线实验
为验证上述失速预警方法的可靠性,进行了针对不同压气机实验台和不同工况的实验研究[54,56].这里以北航单级亚声速压气机TA36 实验台为例,说明该预警方法的有效性.
图16 展示的是周向均匀布置的8 只动态传感器采集到的压力信号,可以在失速前0.05 s (2.5转) 观察到Spike 型失速先兆波.图17 展示了TA36 在设计转速下利用上述方法的在线预警结果,图的第1 行为采集到的压力信号,第2 行为在线实时统计的Rc值,第3 行为在线实时统计的F(Rcth) 值,第4 行为流量系数随时间的变化,阈值Rcth设置为0.9.可以看出,压气机工作点在远离失速点时,F(Rcth)值在0 附近,而当靠近失速点时F(Rcth) 值逐渐增大.将预警警戒值设置为5%和10%时,该方法分别可以在失速前4.5 s (225 转)和2.5 s (125 转)发出预警信号,与先兆波出现时间相比预警时间大大提前.

图16 失速先兆实验测试结果[54]Fig.16 Experimental results of stall precursor[54]

图17 设计转速下在线预警结果[54]Fig.17 On-line stall warning at design rotating speed[54]
4 自适应扩稳控制方法
通常来讲,航空发动机的流动稳定性控制可以是传统机匣处理这种采用固定结构实现被动扩稳的方法,也可以是通过调节机构对消失速先兆波实现主动扩稳的技术,无论采用哪种控制策略,其控制规律都是固定的,无法根据发动机的运行工况进行适时的调整.虽然相比于被动控制方法,主动控制技术似乎距离发动机的智能控制更近了一步,但是,正如引言中提到的,主动对消失速先兆的前提是探测失速先兆,这种将同一信号既作为控制量又作为监测量的控制策略必定会受到响应时间的制约.因此,对于未来智能航空发动机的稳定性控制,需要寻找一条兼顾主被动控制优势,且具备工程实践可能的控制技术.在20 世纪50 年代初期,为了解决飞机的自动驾驶问题,自适应控制概念被提出并发展,在当时的飞行器控制领域,人们越来越发现对于某些性能要求较高的飞行姿态进行控制,使用经典的线性控制器很难达到预期的控制效果,因为经典的控制理论并不包含对环境变化的观测与考察,仅仅凭借已有的既定控制规律很难实现在多变环境下对被控对象进行合适的控制.因此,自适应控制开始逐步被重视起来,并且随着电子计算机技术的飞速发展,该控制理论已经得到了充分的现实应用.相比一般的线性闭环控制系统,自适应控制系统多了辨识器环节,该环节可以通过各种系统辨识或参考模型的方式为控制器提供控制律的指导,进而实现对被控对象的最优控制,因此,自适应控制属于现代控制理论中的优化控制方法.自适应控制的被控对象一般具有两个基本特征:强非线性和随机性.对于一般的线性被控系统或者非线性较弱的系统,经典的线型控制理论往往可以得到比较理想的控制效果;而对于非线性较强的被控系统,系统参数往往无法完全获得,并且环境对系统的影响具有一定的随机性,系统状态就无法预知,此时经典的线性控制理论根本无法实现对被控对象的控制,甚至会起到相反的控制效果.自适应控制系统恰恰弥补了这一不足,通过对辨识器对系统参数进行实时辨识,结合预学习得到的控制律数据库指导控制器采取当下最适合的控制规律作用于被控对象,实现对被控对象的控制.
与飞行状态控制的被控对象类似,压气机系统同样具有很强的非线性和随机性特征,该系统任意工作条件下的状态参数同样复杂与不确定.因此,自适应控制系统应该同样能够胜任对压气机系统稳定性的控制,本文在第1、第2和第3 小节中提到,流动稳定性理论预测模型的发展为压气机稳定性设计提供了可靠的评估工具,并为SPS 机匣处理的结构参数设计提供了理论指导;SPS 机匣处理为压气机稳定裕度不足时提供了可行的补救措施;实时失速预警方法可以在压气机运行阶段即将靠近失稳边界时及时发出预警信号.因此,将这三者结合有能力实现压气机自适应扩稳控制系统的构建.
开环控制是实现自适应控制的基础.两者区别在于:开环控制是压气机运行工况接近失稳时失速预警信号触发机匣处理打开并将其结构参数调节到与当前工作状态匹配实施扩稳,这一控制就算完成,之后没有任何操作,即使压气机运行工况又回到远离失速点的位置,机匣处理也处于打开状态;而自适应控制能够根据压气机所处工况调节机匣处理结构参数和开合状态,即当压气机靠近失稳边界时预警技术触发机匣处理打开,此时机匣处理的结构参数为对应工况的最优参数(在扩稳同时尽量保持压升和效率特性),机匣处理结构参数能随压气机靠近失稳程度的不同而做出调整.而当压气机恢复到远离失稳点的工况正常工作时,机匣处理关闭,保持压气机原有的设计特性.可以发现,自适应控制实际上是闭环控制,相比于开环控制增加了机匣处理结构参数及开合状态与压气机工作系统之间的反馈,这也就能保证压气机在远离失稳边界时能够以其常规特性运行,只有在近失稳点才会打开机匣处理.
4.1 开环控制
对于特定的压气机,要实现开环控制,首先需要建立机匣处理控制规律(流量、裕度、效率和压比)的对应数据库.数据库可以通过理论模型对结构参数进行敏感性分析和实验手段直接测试的手段获得.这样,在工作条件发生改变的同时,控制规律能给出机匣处理最优的几何参数配比,从而实现扩稳的目的.
为实现开环控制,如图18 所示设计了可调结构参数的SPS 机匣处理.利用SPS 机匣处理和发展的实时失速预警方法在低速实验台TA36 上实现了全转速的开环稳定性控制,如图19 所示,取得了很好的扩稳效果.

图18 可调几何参数的SPS 机匣处理简图Fig.18 Diagram of SPS casing treatment with adjustable geometric parameters

图19 扩稳目标5.5%下实现的全转速开环稳定性控制效果[56]Fig.19 Open-loop stability control at 5.5% object of stall margin enhancement[56]
4.2 自适应控制
结合SPS 机匣处理和失速预警技术,在开环控制的基础上增加机匣处理结构参数与开合状态对压气机系统的反馈,使机匣处理能够根据压气机工作状态及时调整开合状态和对应的最佳几何参数,实现全工况的自适应扩稳控制,控制流程如图20 所示.

图20 自适应扩稳控制流程图Fig.20 Flowchart of adaptive control
图21 给出了低速压气机实验台TA36 上实现的自适应扩稳控制的在线监测.图中第1 行为通过转子前机匣壁面安装的静压传感器检测到的压力值计算得到的Rc值,第2 行为实时计算的F(Rcth) 值,第3 行为流量系数.阈值Rcth设置为0.8,预警警戒值设置为0.6.可以看出,当流量系数较大时,F(Rcth)几乎为0,随着节流过程的进行F(Rcth) 开始逐渐增大.当F(Rcth) 值增大至预警警戒值0.6 时发出预警信号,控制系统触发SPS 机匣处理的开关,使其打开斜槽并使穿孔率等几何参数达到预设值.此时F(Rcth)值会随着SPS 机匣处理的打开而逐渐减小,当减小到一定程度触发SPS 机匣处理关闭,之后F(Rcth) 又会再次增加,当达到警戒值时再次发出预警信号触发机匣处理打开.这样就实现了压气机自适应的扩稳控制.使用自适应扩稳控制方法在低速实验台TA36 上的实验结果如图22 所示,可以看出,在全转速范围内下都实现了压气机的扩稳控制.

图21 在线自适应控制监测结果[56]Fig.21 Online adaptive control results[56]

图22 全转速SPS 机匣处理自适应控制效果[56]Fig.22 Adaptive control effect of SPS casing treatment at different rotating speeds[56]
5 总结
本文综述了作为未来航空发动机智能控制关键技术的压气机流动稳定性自适应控制方法研究领域的相关进展,主要包括压气机流动稳定性通用理论、壁面阻抗边界扩稳方法、在线实时失速预警方法和自适应扩稳控制方法等.
(1)基于线性全局稳定性分析的叶轮机流动稳定性通用理论.该方法能够考虑压气机内部流动的三维非均匀性,并通过将叶片几何模化为体积力源项的方法考虑叶片三维几何的影响,将流动失稳问题转化为数学上的特征值问题,通过特征值虚部正负来评估压气机系统稳定与否,判据清晰,预测精度高,且具有工程上可承受的计算资源和时间消耗.这为压气机设计阶段提供了快速可靠的流动稳定性评估工具,减弱了稳定性设计的不确定性,降低了设计成型的压气机在试车阶段裕度不达标的风险.
(2)基于壁面阻抗边界调控的SPS 机匣处理和泡沫金属机匣处理扩稳方法.其核心思想是利用波涡相互作用机制构建壁面阻抗边界来耗散扰动波的能量,这相当于为压气机系统提供了一种非定常边界条件,从而抑制失速先兆波的非线性放大来实现扩稳.借鉴气动声学的发展,采用等价分布源方法将机匣处理描述成阻抗边界条件,结合传递单元方法和模态匹配方法,建立考虑机匣处理的压气机失稳预测模型.该模型能够对机匣处理的关键结构参数进行敏感性分析,从而为机匣处理优化设计提供理论准则.实验证明,SPS 机匣处理扩稳效果显著,且能保持压气机原有的压比和效率特性.泡沫金属机匣处理具有扩稳降噪双重收益,工程应用前景广阔.
(3)基于气动声学原理的在线实时失速预警方法.通过对压力扰动波的理论推导,建立了转子上游机匣壁面上动态压力传感器检测到的静压与叶片环量(叶片载荷)之间的关系,并阐明了压气机在远离失速工况时该压力信号在一个或几个转子周期内具有时间准周期性,而靠近失速边界时该周期性会被破坏.基于该机制定义了衡量时间周期性的参数并通过引入概率分布函数实现了秒量级以上的在线失速预警,预警时间大大提高.
(4)基于SPS 机匣处理和实时失速预警方法的压气机自适应扩稳控制方法.通过建立压气机工作状态与机匣处理结构参数及开合状态之间的反馈,建立了闭环控制系统,使得压气机在远离失稳点时保持其设计特性运行,只有在靠近失稳时才会打开SPS 机匣处理并将其几何参数调整到需要的最佳配比.为未来航空发动机智能控制提供了一种主/被动相结合的自适应控制方法.
本文符号表详见附录.
附录

符号表
