固相颗粒粒径对浆体流变特性影响的实验研究
2022-04-07孙志高王晓春
张 页 孙志高 刘 行 王晓春 李 娟
(苏州科技大学环境科学与工程学院 苏州 215009)
冰浆因较好的传输性能和较高的融化潜热,受到学者们的广泛关注[1]。这是一种新型环保浆体,由冰晶粒子、水和凝固抑制剂组成,其中冰晶粒子的平均特征直径不超过1 mm[2]。冰浆既可作为冷量的换热介质,又可作为冷量存储的储冷介质[3],已广泛应用于建筑蓄冷、食品加工、医疗保护等众多领域[4-6]。冰浆的蓄冷应用有助于实现电力“移峰填谷”,起到均衡电网负荷的作用[7]。
常见的冰浆制备技术有刮削法、过冷法、直接接触法等[8-10],但在制备过程中准确控制冰晶颗粒大小的技术还尚未成熟。此外,在存储及运输过程中,由于熟化、团聚、破碎等动力学行为的存在,冰晶颗粒的尺寸会不断发生变化[11-13],难以通过冰浆实验来衡量冰晶粒径对冰浆流动特性的影响。因此本文挑选与冰晶密度接近的聚乙烯颗粒,在确保固相颗粒大小不变的情况下,进行固液两相流流动特性的基础实验研究。
B. Stutz等[23]使用密度接近冰的聚丙烯小球进行实验,解释了冰浆在管道内的流动行为。杜军恒[24]利用聚乙烯颗粒代替冰晶颗粒进行流动实验,观察了固相颗粒在水平圆管和弯管内流动时的分布情况。M. Darbouret等[25]发现TBAB水合物浆体的流动符合Bingham模型,但Ⅰ型TBAB水合物和Ⅱ型TBAB水合物的流变行为存在差异,这是由于Ⅰ型TBAB水合物和Ⅱ型TBAB水合物的粒子形状大小上的差异造成。A. Kitanovski等[26]发现当冰浆呈均质床流动时,冰晶粒径对黏度的影响很低,但是当流速较低时,由于管道顶部区域浓度较高,冰晶粒径对黏度的影响无法忽略。因此,本文选用密度约为0.922 g/cm3的聚乙烯颗粒代替冰晶颗粒进行实验,控制固相粒径,模拟冰浆在水平圆管内的流动,确定适用于混合浆体的流变模型,并分析固相粒径对流变特性的影响,为冰浆的实际应用提供理论依据。
1 实验材料及装置
1.1 固相和液相工质
选用密度约为0.922 g/cm3的聚乙烯颗粒作为冰晶(密度为0.920 g/cm3)的替代颗粒,筛选三种粒径的聚乙烯颗粒进行实验。每种粒径随机各取50颗样品,用游标卡尺(精度:±0.03 mm)测量每个样品的粒径,取平均值作为该组实验固相颗粒的实际尺寸,表1所示为样品颗粒的测量结果。
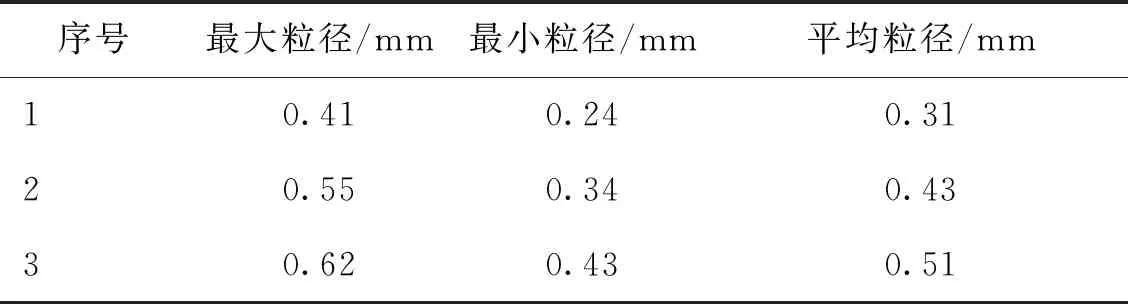
表1 固相颗粒的样品尺寸
液相为实验室自制纯水,在冰浆的流动特性实验中,为避免冰晶聚集,通常会添加一些表面活性剂来增加冰晶在溶液中的分散性。因此,为使聚乙烯颗粒与水形成的固液混合浆体能够达到和冰浆相似的分散效果,实验选用十二烷基硫酸钠(SDS)作为表面活性剂,SDS购于麦克林官网,分析纯。
1.2 实验装置
图1所示为实验装置流程示意图,整个测量系统由载冷剂循环系统、压降测试系统以及数据采集系统组成。图2所示为实验装置照片,该系统可用于冰浆的制取以及冰浆流动换热特性的测量。为研究颗粒粒径对固液两相流流动特性的影响,采用聚乙烯颗粒代替冰晶颗粒。恒温循环水槽是载冷剂循环系统中的主要仪器,型号为DL-3030,制冷量为1 000~3 000 W,实验过程中混合浆体的温度控温范围为-30~50 ℃(精度:±0.01 ℃)。压降测试系统主要包括储存罐、搅拌电机、循环泵、电磁流量计、差压变送器、热电偶等。其中储存罐的内径为60 cm,高为100 cm,材质为不锈钢,罐体上方设有加料口,便于添加实验材料,其余实验仪器的详细参数如表2所示。实验过程中的流量、压降、温度等参数分别由电磁流量计、差压变送器和热电偶采集,并传输至电脑。数据采集设备采用智能设备监控模块,会实时展示、记录和保存实验过程中所有的测量参数,记录时间间隔为10 s。
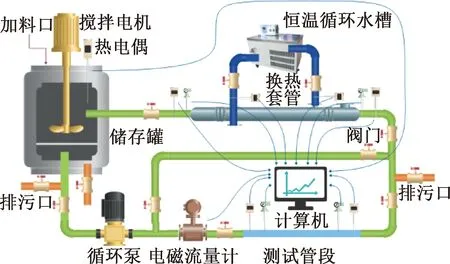
图1 实验装置流程图

图2 实验装置照片
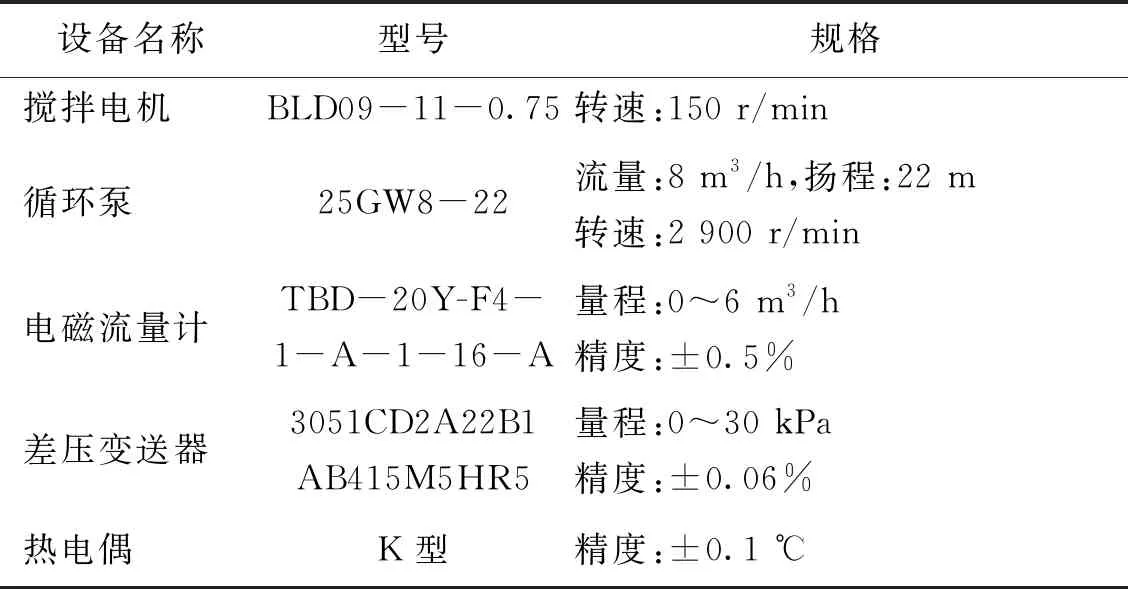
表2 实验仪器参数
实验压降测量管段的详细结构如图3所示。测量段为水平放置的高透明有机玻璃直圆管,圆管外径为32 mm,壁厚为2 mm,长度为3.6 m。压降的测量距离为1 m,为避免流体扰动对测压值产生影响,测压段前设有长为1.8 m的入口段,测压段后为0.8 m的出口段。热电偶设置在测试段前后两处,取两处测量的平均值作为混合浆体的实验温度。测量管段前后通过PVC软管与实验装置相连。

图3 实验测量段详细结构
1.3 固液两相流溶液的配制及实验工况
先用电子计重秤(型号:ZCS,精度:±1 g)称取一定质量的纯水,从加料口倒入储存罐中,使纯水的液面没过搅拌叶片约10 cm;再用电子天平(型号:CP512C,精度:±0.01 g)称取一定质量的SDS加入储存罐中。打开搅拌电机,转速调节至150 r/min,搅拌制备质量分数为0.1%的SDS溶液作为固液两相流的液相工质。然后用电子计重秤按照实验设定固相质量分数称取一定质量的聚乙烯颗粒,配置聚乙烯颗粒与SDS溶液的混合浆体。调节调频器改变循环泵的转速,调节旁通管上阀门的开合大小来控制浆体在测试管内的体积流量,并通过电磁流量计测量。根据体积流量及有机玻璃圆管的内径能够计算得到浆体在管道内的流速。实验中,控制流速为0.05~0.95 m/s,每间隔0.1 m/s进行一次测量,固相质量分数选取为0%、5%、 10%、15%和20%。
1.4 实验台验证
实验装置由本课题组自行设计安装。为验证实验结果的可靠性,使用该装置测量常温条件自来水在管道内的流动压降,将实验测量结果与理论计算结果(理论计算公式见文献[27])进行对比。
已知25 ℃时,自来水的密度为997 kg/m3,运动黏度为0.917×10-6m2/s。理论值与实验值对比如图4所示,实验测得压降与理论压降的最大相对偏差小于7%,在合理的范围内,实验装置的可靠性得以验证。
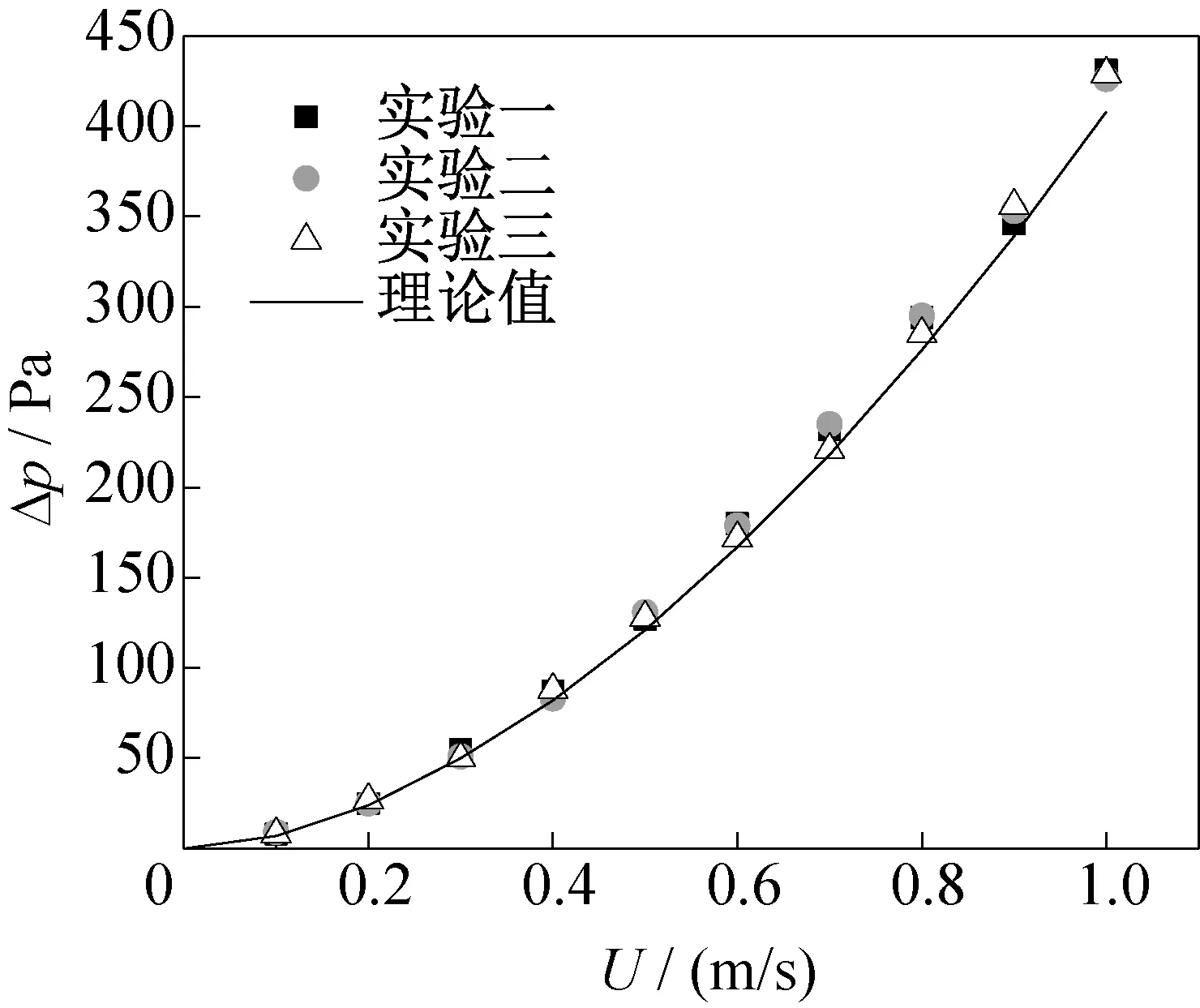
图4 实验压降与理论压降的对比
1.5 实验误差分析
实验过程中存在多个直接和间接测量值,其中,直接测量值质量m、实验管段的长度L、实验管段的内径D、体积流量Q、流动压降Δp的相对误差分别为0.003%、0.02%、0.02%、0.5%和0.06%。根据误差传递公式可得间接测量值相对误差,间接测量值流速U、流动阻力系数λ、剪切应力τ、剪切速率γ的相对误差分别为0.5%、0.5%、0.07%和0.5%。
2 固液两相流的流变模型
流体在水平圆管内流动时,壁面剪切应力与剪切速率满足如下关系:
(1)
(2)
式中:τw为壁面剪切应力,Pa;D为管径,m;L为管长,m;U为流速,m/s;γw为壁面剪切速率,s-1。
冰浆为牛顿流体时,其剪切应力与剪切速率呈线性关系:
τw=μγw
(3)
式中:μ为动力黏度,Pa·s。
冰浆为非牛顿流体时,常用的4种流变模型[16]剪切应力与剪切速率的关系式如表3所示,此处的剪切速率是将浆体视为牛顿流体时的剪切速率。Power Law模型和H-B模型中的n和k分别代表流变指数和流变系数。n的大小能够反映冰浆偏离牛顿流体的程度,当n=1时,浆体表现为牛顿或Bingham流体;当n<1时,浆体表现为剪切稀化流体,即假塑性流体;当n>1时,浆体表现为剪切增稠流体,即胀塑性流体。k的大小可以反映冰浆黏度的大小。根据剪切应力与剪切速率的关系,绘制各模型的流变曲线,如图5所示。

表3 4种常用的非牛顿流体流变模型
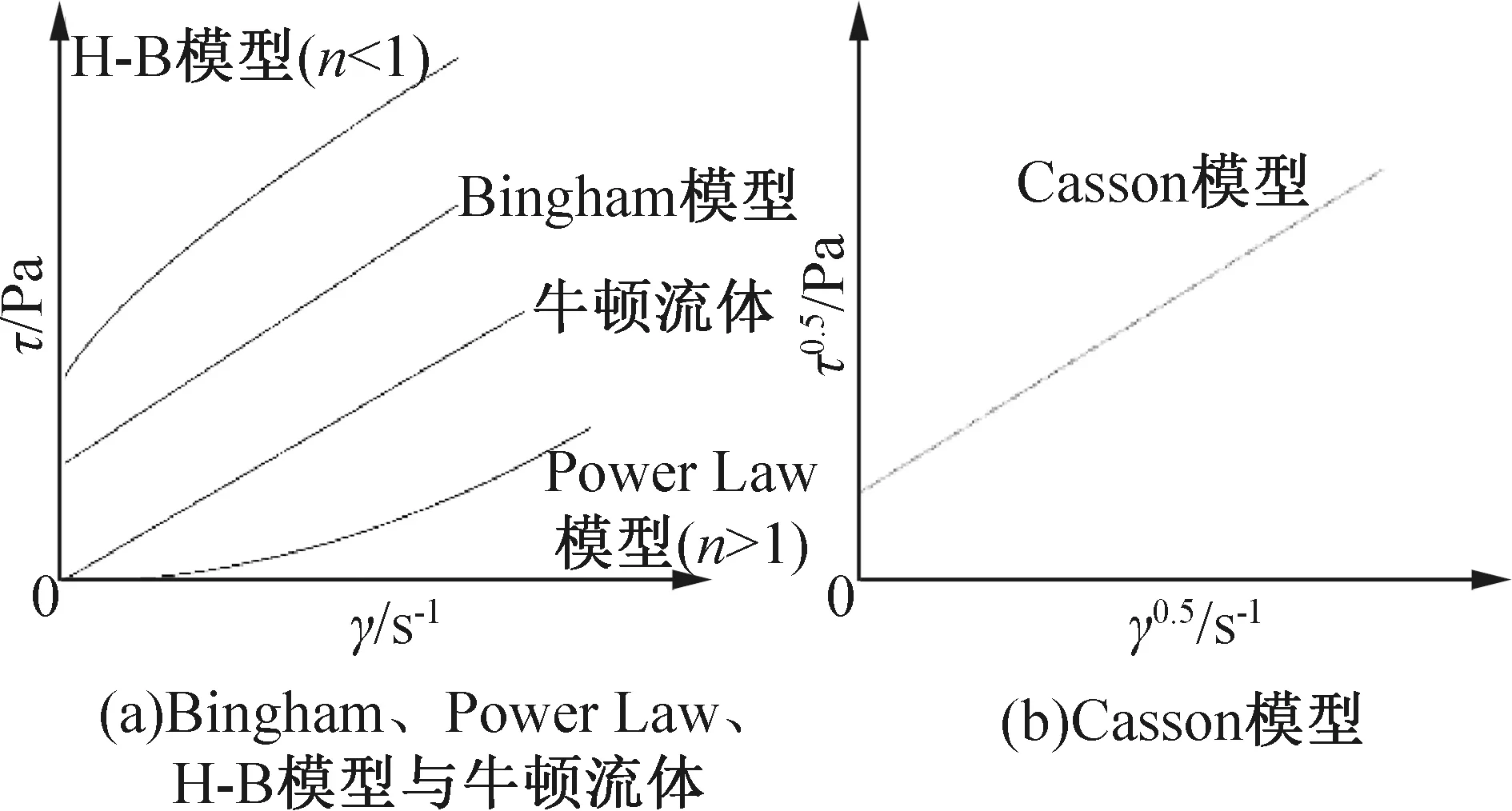
图5 牛顿流体与4种常用的非牛顿流体模型的流变曲线
3 结果与讨论
3.1 剪切应力与剪切速率
根据不同固相质量分数及流速下,实验测量的压降值,利用式(1)和式(2)分别计算出三种粒径下,混合浆体的剪切应力与剪切速率,如图6所示。可以得出以下结论:1)在剪切速率和固相质量分数不变的情况下,增大固体颗粒粒径会引起剪切应力的增加;
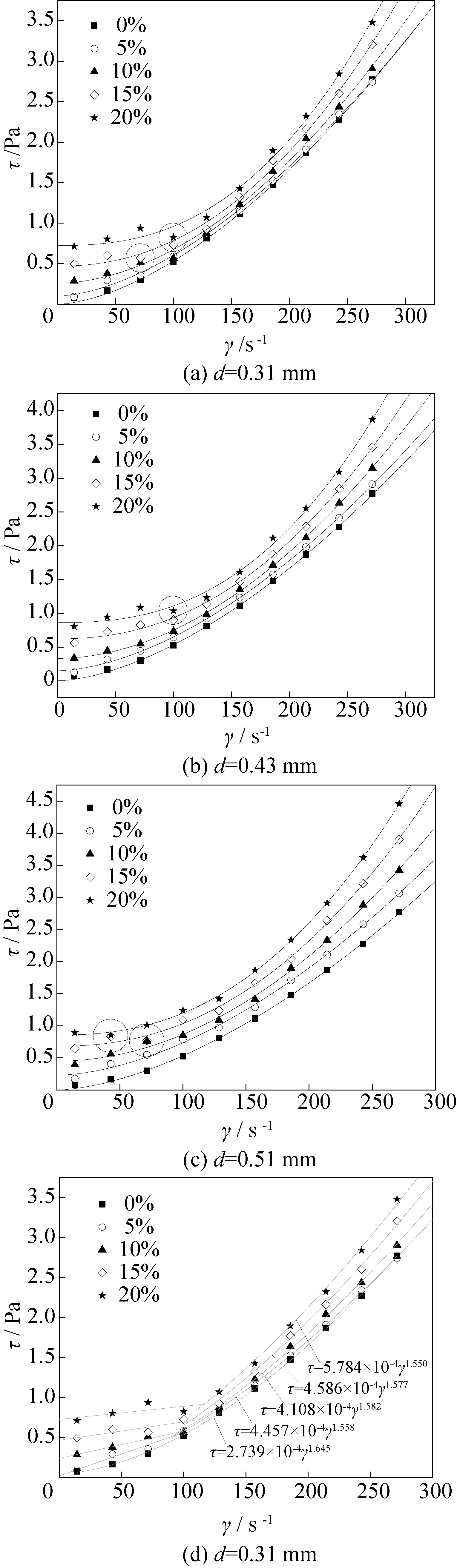
图6 剪切应力与剪切速率的关系
2)对比图中同一剪切速率不同固相质量分数下剪切应力的差值,可知该差异会随着剪切速率先减小再增加;3)混合浆体在流动过程中的剪切应力基本随着剪切速率的增大而呈增大的趋势,但也可能会出现特殊的情况,当剪切速率增大时,剪切应力反而减小,这些特殊的点在图中圈出,出现该现象可能是因为随着混合浆体流动速度的增加,流动形态发生变化引起的。合理利用这样的特殊状态点,可以在提高固液两相混合浆体输运效率的同时降低流动阻力。
3.2 流变模型的适用性分析
1)H-B模型
根据混合浆体剪切应力与剪切速率的关系,首先选择H-B模型进行拟合,如图6(a)~(c)所示,拟合得到的流变曲线与实验数据具有较好的一致性。流变曲线在纵坐标轴上的截距表示浆体屈服应力的大小。当固相质量分数为0时,三种粒径下,混合浆体的流变曲线几乎都经过原点,即屈服应力为0 Pa,所以认为单相溶液符合Power Law模型的流变特性;当固相质量分数大于0时,混合浆体的屈服应力会随着固相质量分数和颗粒粒径的增大而增大。一方面是因为固体颗粒的增多会使混合浆体的黏度逐渐增大,另一方面是因为粒径较大的颗粒在液相中所受的浮力较大,延长了固相颗粒在管道顶部的停滞时间,导致浆体流动起来需克服的应力增大。各粒径下混合浆体通过H-B模型拟合得到的屈服应力如表4所示。
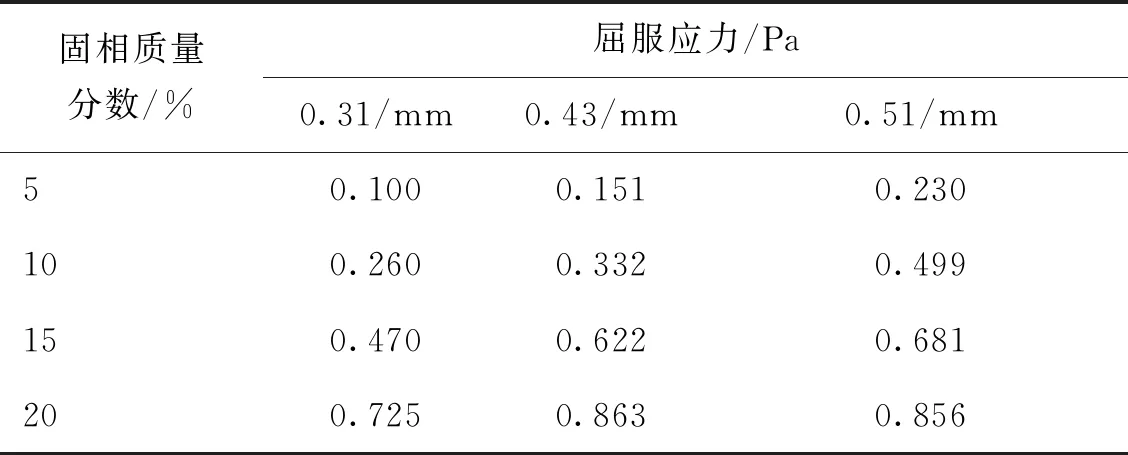
表4 H-B模型拟合得到的屈服应力
2)Bingham和Power Law模型
由图6(a)~(c)可知,流变曲线的非线性增长主要表现在剪切速率较高的情况下,当剪切速率较低时,可以认为曲线基本呈线性增长,剪切速率较高的部分对拟合相关系数的影响大于剪切速率较低的部分,低剪切速率段的流变曲线受高剪切速率段的影响会呈现上扬的趋势,所以直接使用H-B模型进行拟合会高估混合浆体的屈服应力。
为避免流变模型对混合浆体屈服应力的高估,我们提出对固相质量分数大于0的混合浆体的流变曲线进行分段拟合(图6(e)~(f))。以混合浆体满足安全输送的临界流速(浆体转化为悬浮流动时的速度)为分界点,前半段采用Bingham模型进行拟合,获得混合浆体的屈服应力;后半段采用Power Law模型进行拟合,分析混合浆体的流变特性。
本实验中,粒径为0.31、0.43、0.51 mm的混合浆体满足安全输送的临界流速分别为0.35、0.45、0.45 m/s。表5 所示为各粒径下混合浆体通过Bingham模型拟合得到的屈服应力。与H-B模型拟合的结果(表4)相比,可以发现在流速较低时,Bingham模型的精确度要高于H-B模型,Bingham模型得到屈服应力的较小,这与王福晋[28]的研究结论一致,而在流速较大时,H-B模型误差更小。这可能是由于流动速度大小不同时,混合浆体流动形态不同导致。
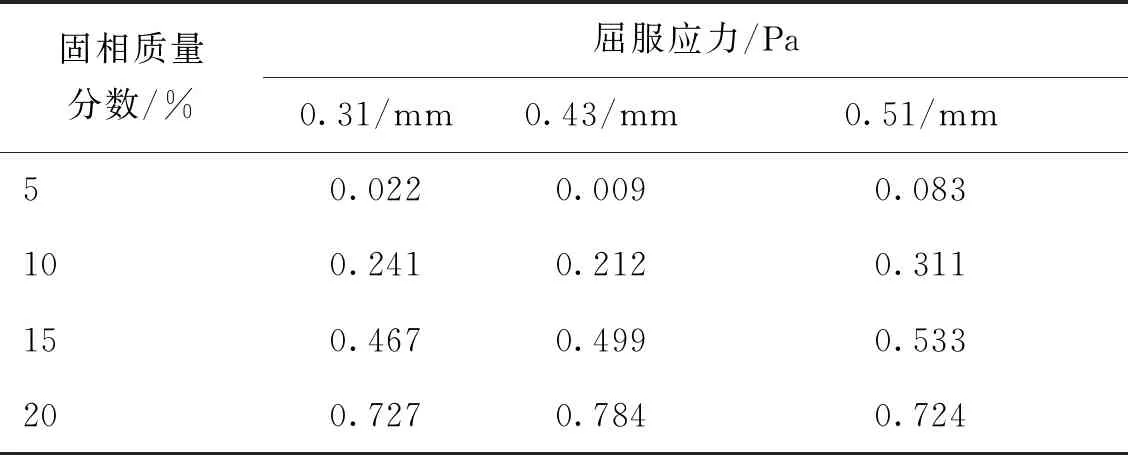
表5 Bingham模型拟合得到的屈服应力
根据Power Law模型的拟合结果(图6(e)~(f)),绘制出混合浆体的流变指数和流变系数与固相质量分数和粒径的关系,如图7所示。混合浆体的流变指数n总是大于1,说明混合浆体为胀塑性流体,并未发现固相质量分数和粒径对流变指数一致的趋势性影响规律(图7(a))。当颗粒粒径不变时,混合浆体的流变系数会随着固相质量分数的增大而增大(图7(b)),说明固体颗粒的增多会使混合浆体的黏度增大,这与M. Darbouret等[25]得到的结论一致。同时文献[25]还发现在相同固相质量分数下,Ⅰ型TBAB水合物比Ⅱ型TBAB水合物的黏度低。即粒径较小时的流变系数低于粒径较大时的流变系数,这与图7(b)也较为相似。当固相质量分数小于15%时,粒径对混合浆体黏度的影响较为显著,流变系数随粒径的增大基本呈增大的趋势;当固相质量分数大于15%时,三种混合浆体的流变系数相差较小,因此认为当固相质量分数达到一定值时颗粒粒径对混合浆体黏度的影响会减弱,这与A. Kitanovskid等[26]的观点较为相似,他认为在均质流中,粒径对浆体黏度的影响很小,而Power Law段正好处于安全输送流速区域,因此,流变系数相差较小。但同时不应忽略固相质量分数对黏度的影响。
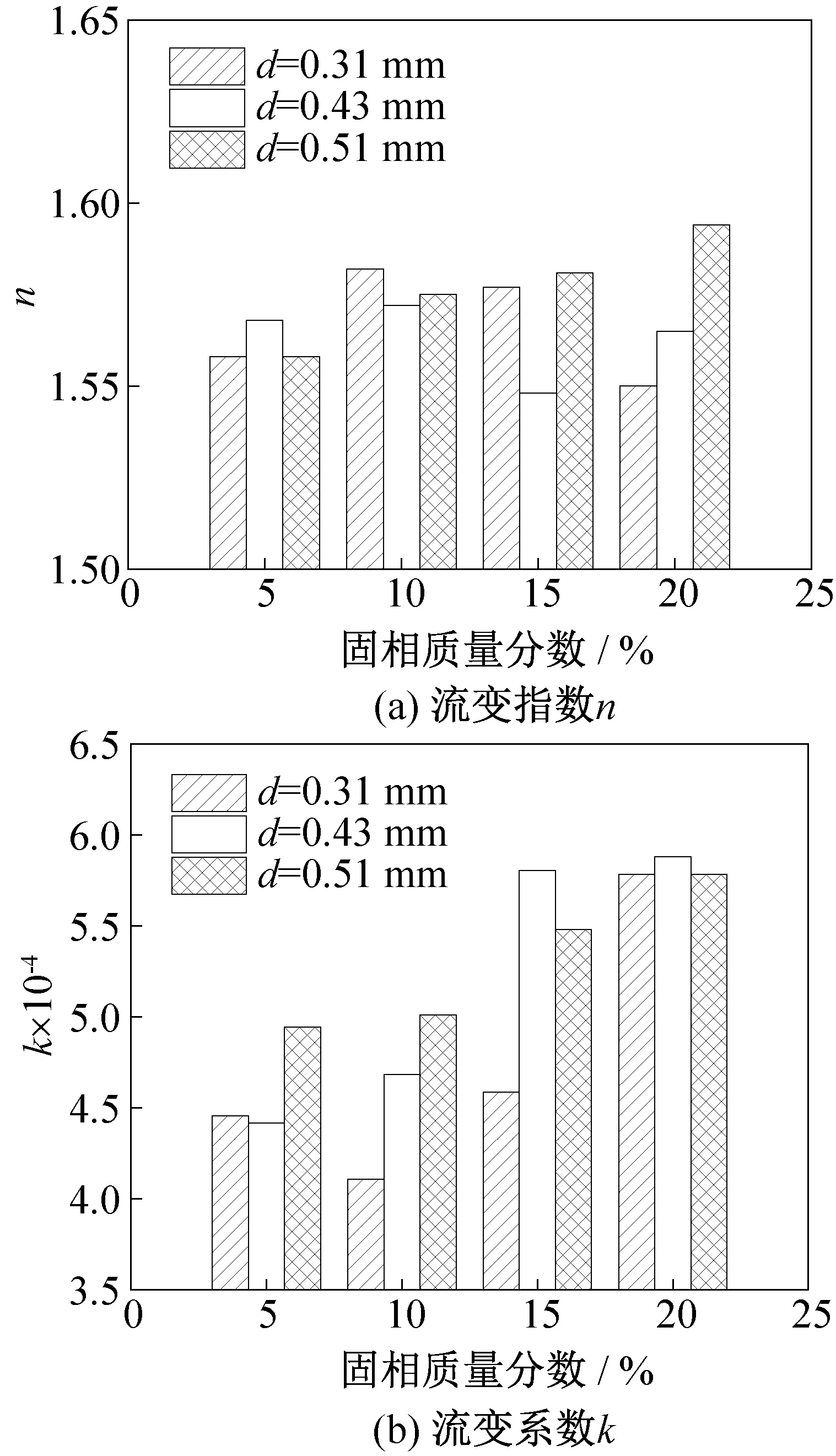
图7 流变指数、流变系数与固相质量分数的关系
3.3 混合浆体的流动阻力系数
1)实验测量流动阻力系数
根据达西公式[27],得到混合浆体在水平有机玻璃圆管内的流动阻力系数。图8所示为不同粒径的混合浆体在不同流速下阻力系数的变化规律。在固相质量分数和粒径一定的条件下,混合浆体的阻力系数基本随着流速增加呈逐渐减小的趋势。在低流速区,高固相质量分数下混合浆体的流动阻力系数与低固相质量分数下的相比,出现大幅增长。这是因为流速越低、固相质量分数越高,固相颗粒越容易在管道顶部堆积聚集,颗粒与管壁之间的摩擦作用不断增强,从而增大了能量损耗。
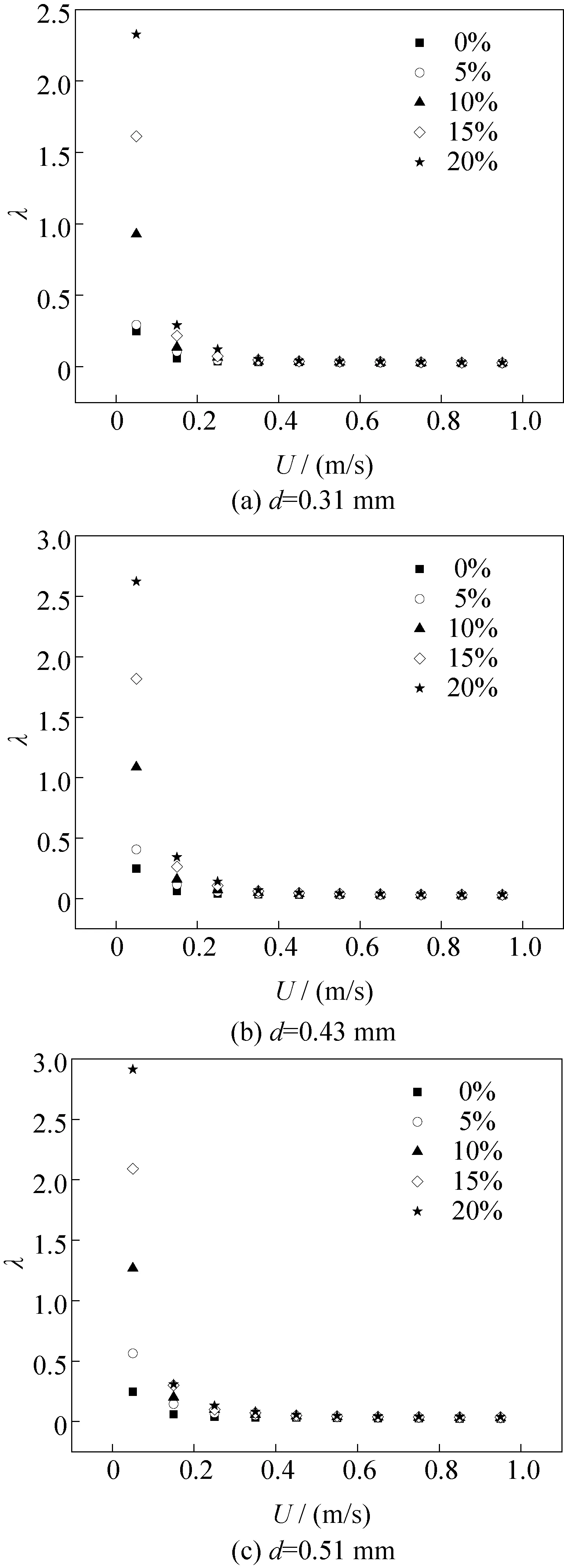
图8 流动阻力系数与流速的关系
为了清晰地观察固相颗粒粒径对流动阻力系数的影响,选取流速在0.25~0.95 m/s内,固相质量分数分别为5%和20%时的阻力系数进行对比,如图9所示。可以发现,在流速和固相质量分数相同的情况下,混合浆体的阻力系数会随着固相粒径的增大而增大。
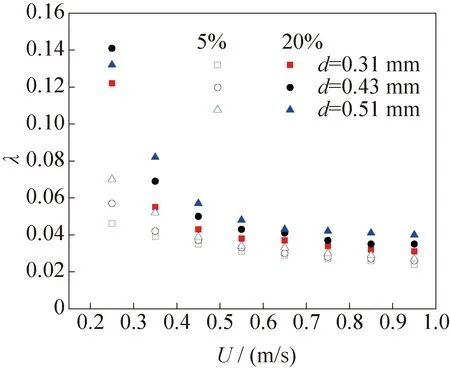
图9 三种粒径混合浆体阻力系数的对比
2)理论计算流动阻力系数
由上节可知,混合浆体会表现出非牛顿流体的特征。针对不同的流变特性,可以通过不同的经验公式计算出冰浆的流动阻力系数。当浆体表现为Bingham流体[19-20]时,公式如下:
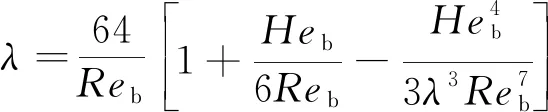
(4)
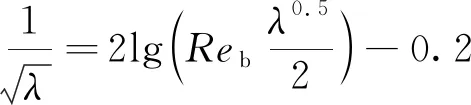
(5)
(6)
(7)
式中:Reb为Bingham流体的雷诺数;Heb为赫斯特罗姆数;τb为屈服应力,Pa;ρsl为冰浆的密度,kg/m3;μsl为冰浆的动力黏度,Pa·s。
当浆体表现为Power Law流体,层流时的流动阻力系数的计算公式和湍流公式如下[23]:
(8)
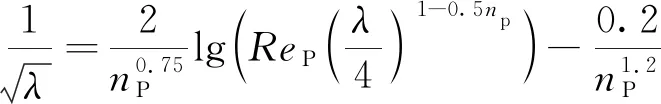
(9)
(10)
式中:Rep为Power Law流体的雷诺数;np为流变指数;kp为流变系数。
冰浆类两相流的流动非常复杂,关于其流态还未确定统一的划分标准。因此,本文参照文献[17,20],认为混合浆体流态变化的临界雷诺数为3 000。基于Bingham和Power Law模型,预测混合浆体在水平圆管内的流动阻力,与实验值进行对比,如图10所示。由图10可知,用Bingham模型预测的阻力系数与实验值之间的误差较大(图10(a)),最大相对误差达90%,这是因为当流速较低时,固相颗粒无法充分分散在载流液体中,混合浆体处于非均质流动的状态,固相颗粒的非均匀性的分布使得浆体的流动阻力激增,导致预测值与实验值的误差增大。图10(b)中Power Law模型阻力系数的预测值与实验值之间取得了良好的一致性,相对误差可控制在±12%以内。
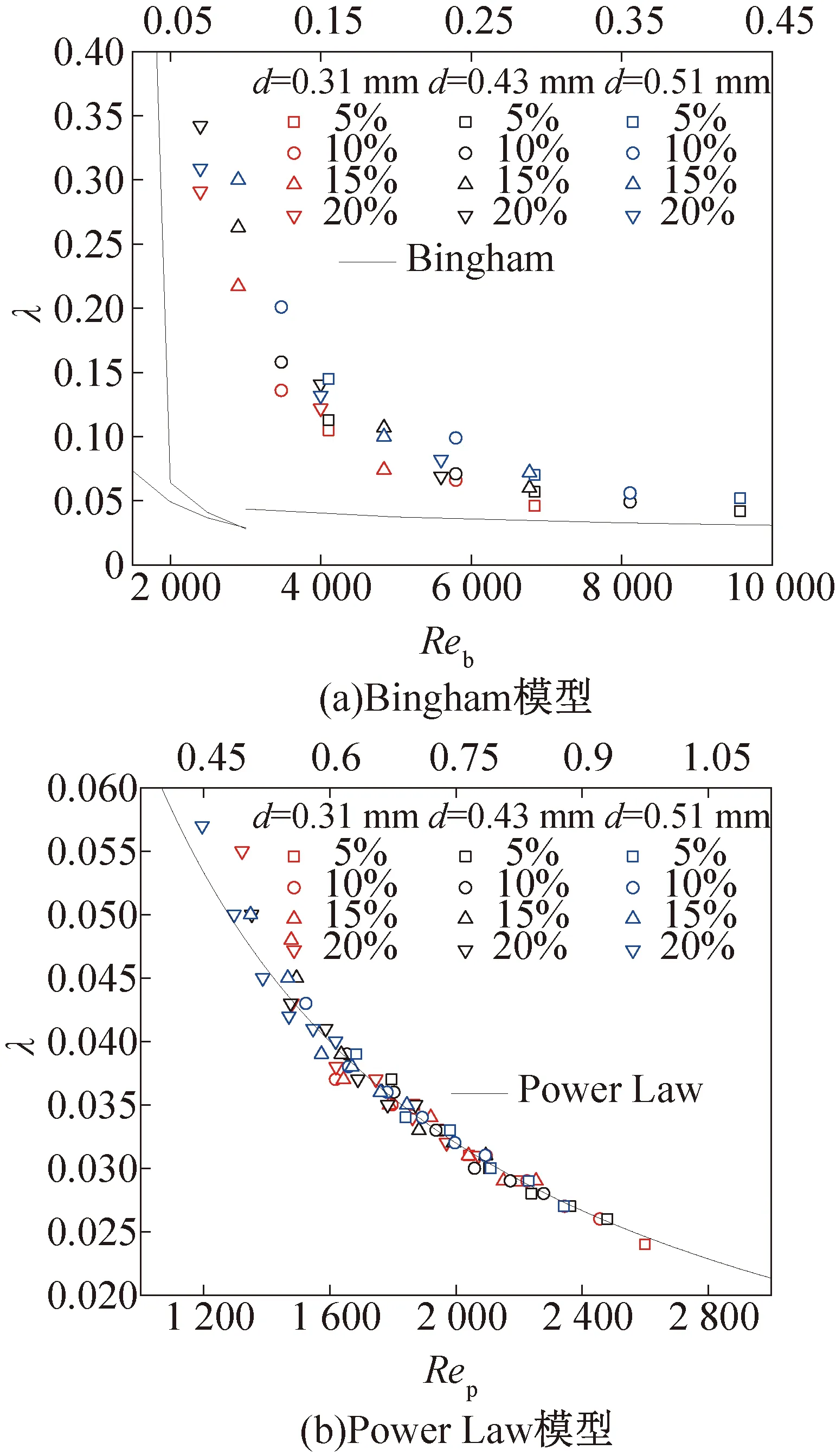
图10 理论摩擦阻力系数与实验摩擦阻力系数对比
4 结论
选用密度约为0.922 g/cm3的聚乙烯颗粒作为固相,固相颗粒的平均粒径分别为0.31、0.43、0.51 mm,测量固相质量分数在0~20%范围内,流速由0.05 m/s变化至0.95 m/s时,混合浆体在水平圆管内的流动压降。根据浆体剪切应力与剪切速率的关系,结合流变模型,分析了在保证固相颗粒粒径大小不变的情况下,固相颗粒粒径大小对冰浆类固液两相流流变特性的影响,得到结论如下:
1)在剪切速率和固相质量分数不变的情况下,颗粒粒径从0.31 mm增至0.51 mm会引起混合浆体剪切应力的增加。当颗粒粒径和固相质量分数一定时,浆体的剪切应力整体基本呈现出随剪切速率增大而增大的趋势,但在某处可能会出现剪切速率增大,如粒径为0.31 mm,固相质量分数为15%,剪切速率为71.43 s-1时,但剪切应力减小的现象,这可能是因为随着流速的改变,混合浆体流动形态发生变化引起的。利用这样的状态点,能够达到提高固液混合浆体颗粒输运效率同时降低流动阻力的目的,在实际工程中会有较好的应用。
2)对混合浆体的流变曲线前半段采用Bingham模型拟合,后半段采用Power Law模型拟合,这样有利于避免高估屈服应力。同时,得到的屈服应力随着固相质量分数以及粒径的增大而增大。浆体表现为剪切增稠流体,其流变指数总是大于1,在颗粒粒径一定的情况下,浆体的流变系数会随着固相质量分数的增大而增大。当混合浆体的固相质量分数较少时,粒径对流变系数影响较为显著,流变系数会随着粒径的增大而增大,而当固相质量分数逐渐增多时,粒径对流变系数的影响会逐渐减弱。
3)混合浆体的阻力系数会随着颗粒粒径增加、固相质量分数提高以及流速降低而增加。基于Bingham和Power Law模型,分别预测了混合浆体在低流速以及高流速下的流动阻力系数。其中Power Law模型能够较为精确的预测混合浆体在较高流速下的阻力系数,最大相对误差小于12%;由于流动形态的影响,Bingham模型在低流速下的预测值与实验值之间的误差相对较大,最大相对误差可达到90%。
本文受苏州市科技发展计划项目(SNG2018045)和江苏省自然科学基金项目青年基金项目(BK20170382)资助。(The project was supported by Suzhou Science and Technology Development Plan Project(No.SNG2018045)and Natural Science Foundation Project Youth Foundation Project in Jiangsu Province(No.BK20170382).)
