基于耗散理论的强夯地基处理夯沉量计算与分析

赵民，桑松魁，白晓宇*

(1.青岛理工大学土木工程学院，青岛 266520; 2.青岛市勘察测绘研究院，青岛 266033)

耗散理论是研究远离平衡态的开放系统，通过不断与外界交换能量与物质，从原有的无序状态到有序状态的演化规律的一种理论。它提出非平衡态是有序之源，非线性作用是有序的动力[1]。它摆脱了经典理论的思维方式，在岩石学、物理学、建筑学等众多领域的研究中取得了丰硕的成果[2-5]。对于强夯过程而言，开放性、不平衡、非线性是绝对的，而封闭性、平衡、线性则是相对的。随着耗散理论以及非线性动力学的创立，应用新的思维来考虑强夯中的问题成为一种可能。

在强夯加固效果方面，国内外学者运用多种方法进行了研究。Lo等[6]通过对现场数据的整理分析建立了场地平均夯沉量与单击夯击能及土质条件的经验方程。Takada等[7-8]通过强夯模型试验与现场试验的对比得出，夯沉量与锤的动量、夯击次数的平方根成正比，与夯锤底面积成反比。牛志荣等[9]通过数值分析研究了土为拟弹性体时土的振动特性，并得出了沉降计算的方法。刘春等[10]运用波动理论对强夯施工时瞬时过程对地基所产生的影响进行了研究，推导出饱和土的波动方程和超静孔压的特解方程。贾敏才等[11]运用相似理论建立砂土的细观颗粒流模型，对强夯加固砂土地基时动力响应进行研究，是首次从细观角度揭示强夯砂土的动力响应特性。就研究现状可知，强夯法加固效果的研究仍以区域性经验数据和经验积累为基础，由于数值模拟等方法得出的计算方法及关系的适用性较窄，目前关于夯沉量变化和能量传递等问题未得到较好解决。

针对上述研究问题，现以现有强夯边界问题的解答为基础，建立碎石素填土地基的夯击效能系数公式，并利用工程实测结果，得到夯击能与土体密度不同组合下夯沉量随夯击次数的变化曲线，揭示夯沉量的变化规律，结合耗散理论对夯沉量变化过程中夯击能量的耗散过程进行分析。

1 研究方法和数据采集

1.1 耗散结构基本理论

比利时物理化学家Prigogine于20世纪70年代创立了耗散结构理论，用以研究系统在远离平衡态的条件下，由于其内部的非线性相互作用，而发生从无序热力学分支向耗散结构分支转化，并形成一种稳定的有序结构的现象，如图1所示。该理论强调当一个体系接近平衡时原有的结构就会趋于消亡，只有当体系远离平衡时才能产生新的有序结构[12]。远离平衡态的开放系统(力学的、生物的、社会的、经济的)，当外界条件或系统的某个参量变化到一定的临界值时，通过涨落发生突变，即非平衡相变，并不断地与外界交换物质、能量与信息，系统从原来的混沌无序状态转变为一种时间、空间或功能上的宏观有序结构[13]。

图1所示的C点为临界点，当控制量超过临界点的临界值时，系统会出现从平衡态连续过度来的热力学分支突然失稳，进而跃迁到稳定的耗散结构分支，发生非平衡相变。非平衡相变的演化过程，是系统各元素之间的非线性相互作用并使各要素之间产生协同作用和相干效应的结果。

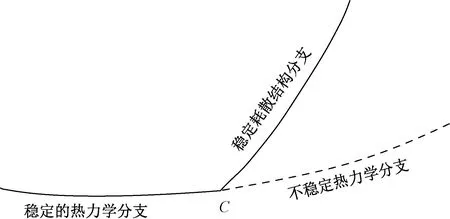
图1 热力学分支失稳与耗散结构分支的形成

1.2 强夯过程的耗散结构认识

工程场地土体在变形、破坏等演化过程中与外界存在着物质、能量与信息的交流，所以土体是一个开放的系统[1]。未进行强夯前的土体，土层松散，颗粒之间接触不够紧密，孔隙比较大，处于一种非平衡状态[14]。外界条件一旦发生改变，土体的变形随机性比较大，这样的系统是不稳定的。

强夯连续夯击作用给地基土体提供了能量使地基土体孔隙比减小，密实度增大，夯坑深度逐渐加大，从非平衡热力学角度分析，这些能量的供给通过系统的能量耗散以及非线性动力学来维持。而强夯地基土体变形过程中，土颗粒的形状和位置的变化、塑性硬化、热传导、化学反应等不可逆的变化过程提供了能量耗散和非线性动力学机制，从而使强夯作用下地基土体表现为一种耗散结构。

强夯作用下岩土体的变形演化是由土体结构、含水量、夯能等形成的子系统共同作用所体现的一种综合现象，表现为土颗粒定向排列，大孔隙减少减小，向微孔隙聚集，夯击效能趋于稳定时，土体孔隙比逐渐减小至趋于极限孔隙比[15]，宏观表征为单击夯沉量减小并趋于某稳定值，从变形的角度可以认为此时地基土体已经被夯实。

1.3 强夯过程中夯击效能系数的计算

强夯过程中冲击荷载所做的总功除了土体的阻尼和回弹消耗外，还有一部分能量被耗散掉。能量耗散理论中，耗散能为系统向稳定态进化过程中，为维持这种稳定状态所消耗的能量。而强夯过程中土体向稳定状态进化的宏观表现为夯沉量的变化，土体达到新的稳定状态的宏观表现为夯沉量趋近于某一稳定值。所以强夯过程中的耗散能等于冲击荷载所做的总功(W1)减去土体的阻尼和回弹消耗能量(W2)，定义夯击过程中的耗散能为夯击效能，公式为

W=W1-W2

(1)

定义夯击效能系数η为

η=(W1-W2)/W1

(2)

则夯击效能系数推导如下。

钱家欢等[16]在Socct公式的基础上，运用结构动力学理论，推导出强夯加载和卸载过程的应力和位移随时间变化曲线。

加载阶段：

(3)

加载历时：

(4)

卸载阶段：

(5)

卸载历时：

(6)

残余沉降：

(7)

夯击总历时：

(8)

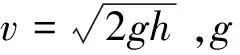
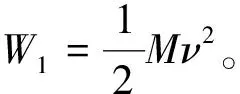
(9)

定义夯击因素为

λ=M/ρr03

(10)

则夯击效能系数η与泊松比μ、夯击因素λ及E/Esul有关。

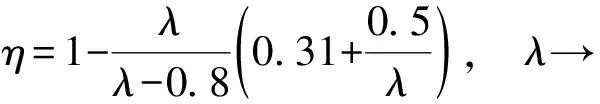
(11)

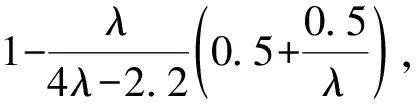
λ→∞，η→87.5%

(12)

由式(11)和式(12)可知η与λ成正相关，又由式(10)可知λ与ρ呈负相关。所以η与ρ呈负相关，与M成正相关。

通过对耗散理论的分析，计算得到了夯击效能系数，依据耗散理论和夯击效能系数与夯击能之间的关系，开展了现场强夯试验。通过引入夯击效能系数，分析了现场试验在相同夯击能和不同夯击能作用下，夯沉量与夯击效能系数的内在联系。

1.4 场地条件及数据采集

某施工场区地形起伏较大，总体东南至西北倾斜，西侧为侵蚀冲沟，其余地段属剥蚀堆积缓坡地貌，后经人工回填改造。设计要求强夯处理后承载力特征值不小于200 kPa。强夯施工前对场区进行回填，填土厚度3～8 m，土质为碎石素填土。回填至标高后进行强夯施工。施工现场1号夯锤重20 t，夯锤直径2.2 m；2号夯锤重10 t，夯锤直径2 m。在试验A区，首先1号夯锤提升10 m进行两遍点夯，夯点间距为5 m×5 m。然后2号夯锤提升10 m进行一遍满夯。在试验B区，1号夯锤分别提升12.5、7.5、5 m进行点夯，夯点间距为5 m×5 m，然后2号夯锤提升10 m进行一遍满夯。施工过程中严格按照《建筑地基处理技术规范》(JGJ 79—2012)[22]和《岩土工程治理手册》[23]要求执行，准确测量并记录单击夯沉量。

夯后在A区选取3个夯点夯沉量数据编号为1-1、1-2、1-3；在B区内选取3个夯点夯沉量数据(每个提升高度分别选取一点)编号2-1、2-2、2-3。

2 结果与分析

2.1 相同夯击能作用下夯沉量分析

2.1.1 相同夯击能、相同土体密度下夯沉量分析

试验A区选取的1-1、1-2夯点在试验A区西侧边线，经过勘察及土工试验可知，回填厚度相同、土质基本相同、土体密度相同。选用夯锤均为1号夯锤，锤重20 t，提升高度10 m。夯沉量见表1，夯沉量随夯击次数变化规律曲线见图2。

由图2可知：1-1、1-2夯点的单击夯沉量和累计夯沉量曲线基本重合。

由式(10)可知，夯击效能系数η与锤重M、土体密度ρ、夯锤半径r0有关。又经过夯前勘察及土工试验，1-1、1-2夯点的土体密度相同。夯锤重均为20 t，所以当夯击次数相同时，两点的η基本相同，单击夯沉量基本相同，所以单击夯沉量、累计夯沉量基本相同。

由表1和图2可知：随夯击次数的增加单击夯沉量逐渐减小，但减小的速率逐渐变缓，最终趋近于某一较小值。随着夯击次数的增加，累计夯沉量逐渐地增加，但增加的速率逐渐变缓，最终累计夯沉量趋近于一个稳定值。

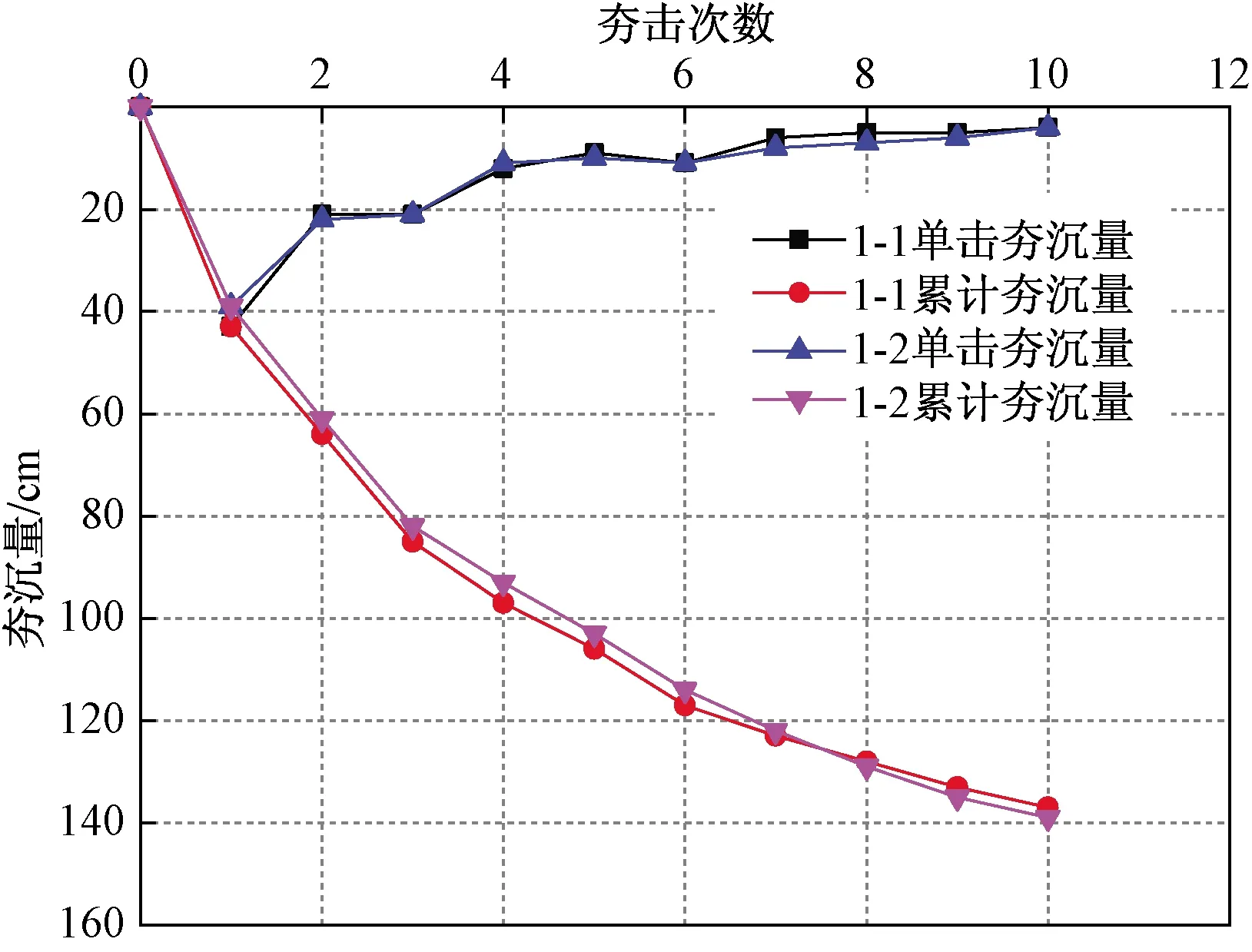
图2 夯沉量随夯击次数变化规律曲线

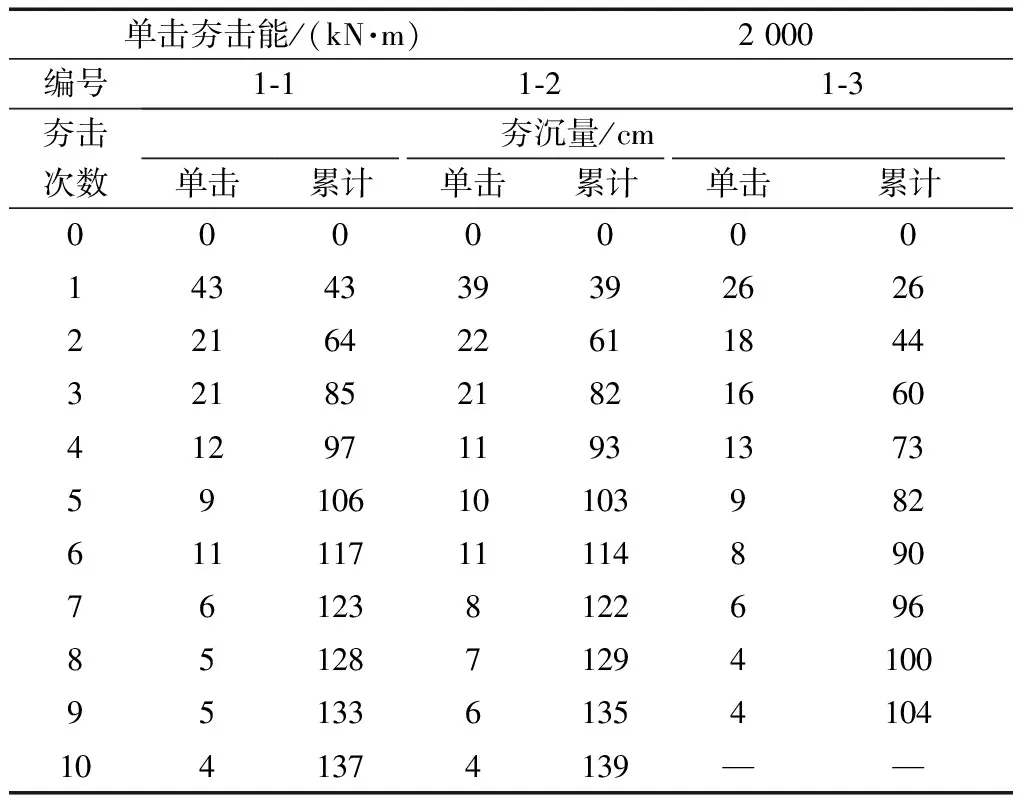
表1 相同夯击能作用下夯沉量数据

在单击夯击能相同的情况下，随着夯击次数的增加，土体的孔隙比逐渐减小，最终趋近于极限孔隙比[15]，土体密度最终趋近于某一稳定值，则夯击效能系数η最终趋近于某一个稳定值，单击夯击效能W趋近于某一个稳定值，则单击夯沉量最终趋近于某一较小值，累计夯沉量趋近与某一稳定值。随着夯击次数的增加，饱和效应[24]的影响越来越大，系统的进化效率逐渐减小，系统逐渐接近稳定状态，所以单击夯沉量减小的速率逐渐变缓，累计夯沉量增加的速率逐渐变缓。

2.1.2 相同夯击能、不同土体密度下夯沉量分析

试验A区选取1-1、1-3夯点。1-1夯点位于试验A区西侧边线，1-3夯点位于试验A区中间位置，经过现场勘察回填厚度相同、土质相同，但经过土工试验测得1-3夯点夯前密度大于1-1夯点。选用夯锤为1号夯锤，锤重20 t，提升高度10 m。夯沉量见表1，夯沉量随夯击次数变化规律曲线见图3。

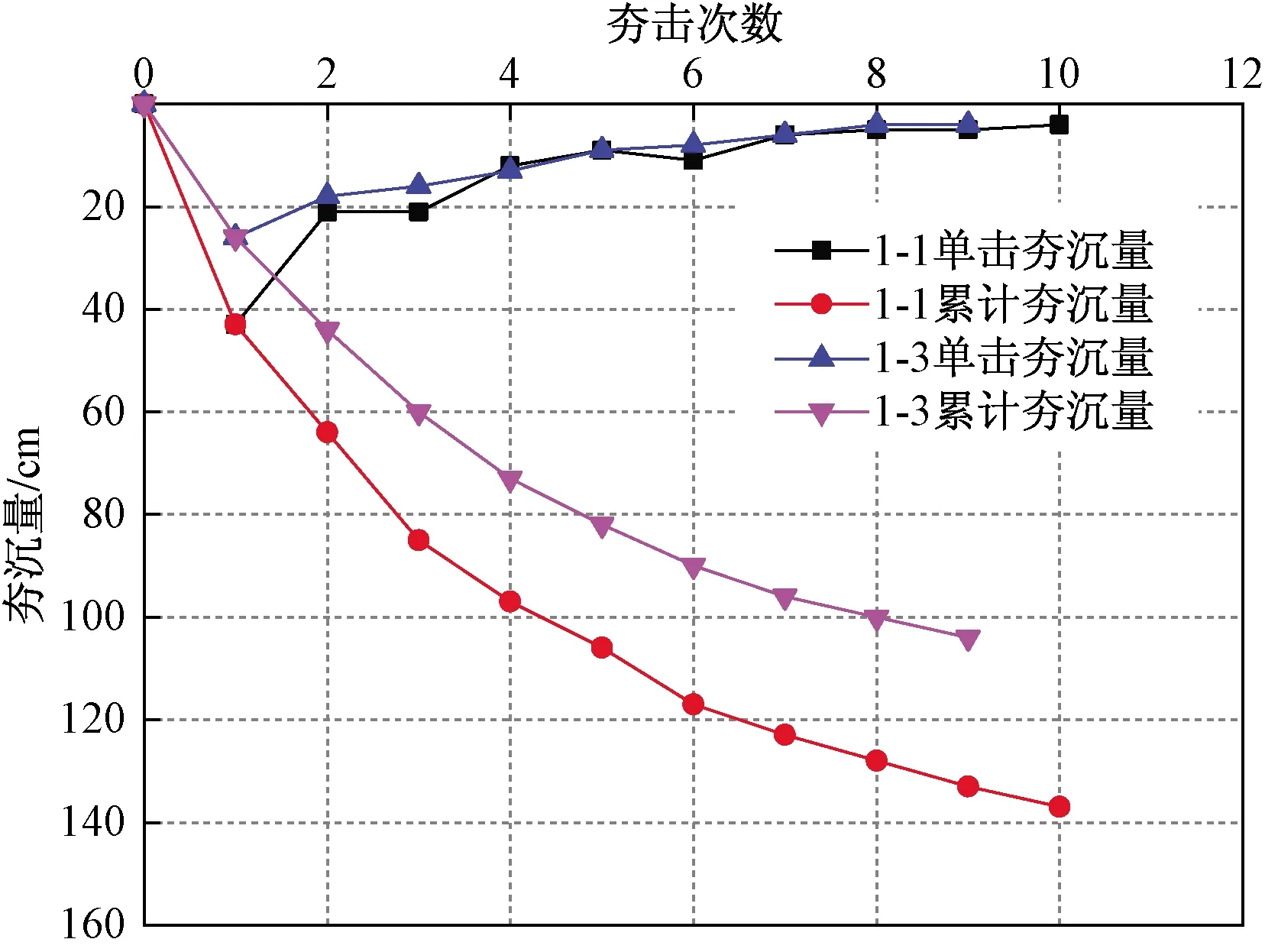
图3 夯沉量随夯击次数变化规律曲线

由图3可知：1-1夯点的最终累计沉降量大于1-3夯点。

夯击前1-3夯点土体的孔隙比较小，密度较大，土体所处的初始稳定状态高于1-1夯点。当同一夯击能对应的最终稳定状态相同时，则夯击时1-1夯点向更高稳定态进化是所需的能量大于1-3夯点，而强夯过程中土体向稳定状态进化的宏观表现为夯沉量的变化，则1-1最终累计沉降量大于1-3最终累计沉降量。

由表1和图3可知：前三次夯击时1-1单击夯沉量明显大于1-3夯点,后续夯击时单击夯沉曲线基本相同。

夯前土体密度ρ1-1<ρ1-3，则由式(12)可知，前两次夯击时1-1夯点的夯击效能系数大于1-3夯点。当单击夯击能相同时，则1-1夯点夯击效能大于1-3夯点，所以前三次夯击时1-1夯点的单击夯沉量大于1-3夯点。随着夯击次数的增加，饱和效应影响越大，系统的进化效率逐渐的减小，夯击效能系数η减小速率变缓，最终趋于某一稳定值，所以后续夯击时单击夯沉量曲线基本相同。

2.2 不同夯击能作用下夯沉量分析

试验B区内选取2-1、2-2、2-3夯点，经过夯前勘察及土工试可知，回填厚度相同，土质基本相同，夯前土体密度相同。夯点2-1：锤重20 t，提升高度12.5 m；夯点2-2：锤重20 t，提升高度7.5 m；夯点2-3锤重20 t，提升高度5 m。夯沉量数据见表2，夯沉量随夯击次数变化规律曲线见图4。

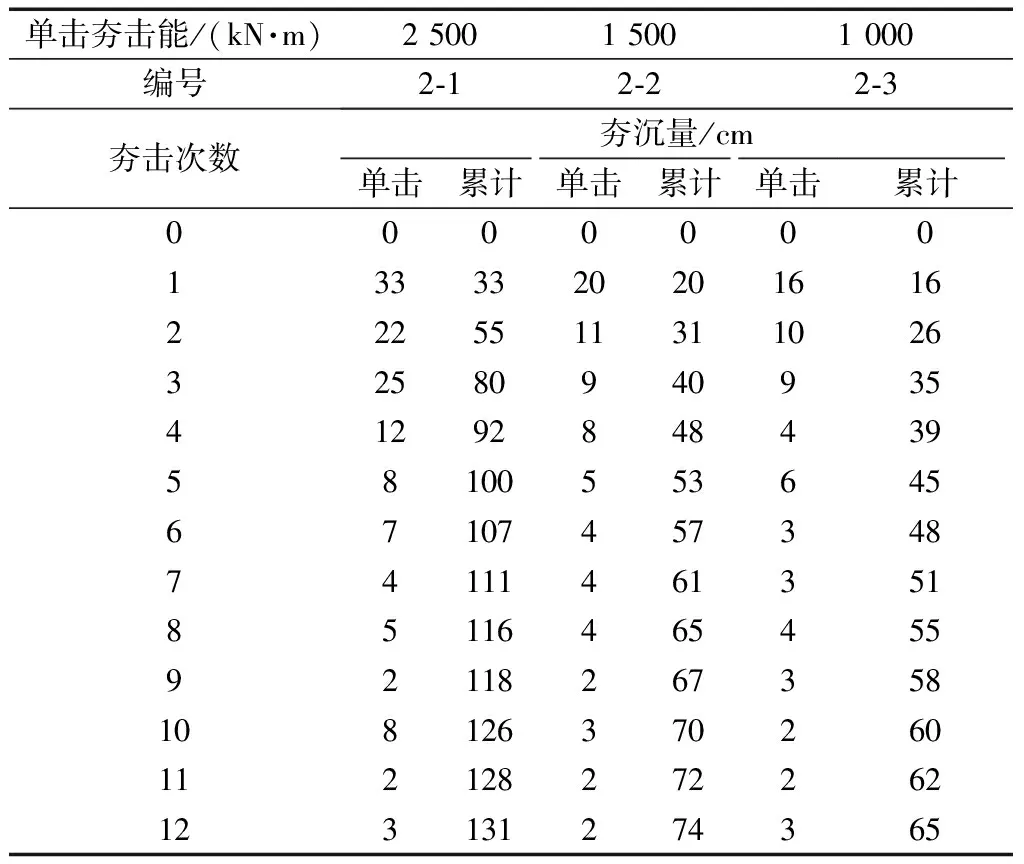
表2 不同夯击能作用下夯沉量数据

由图4可知：在土质条件相同的情况下，单击夯击能越大，累计夯沉量越大。

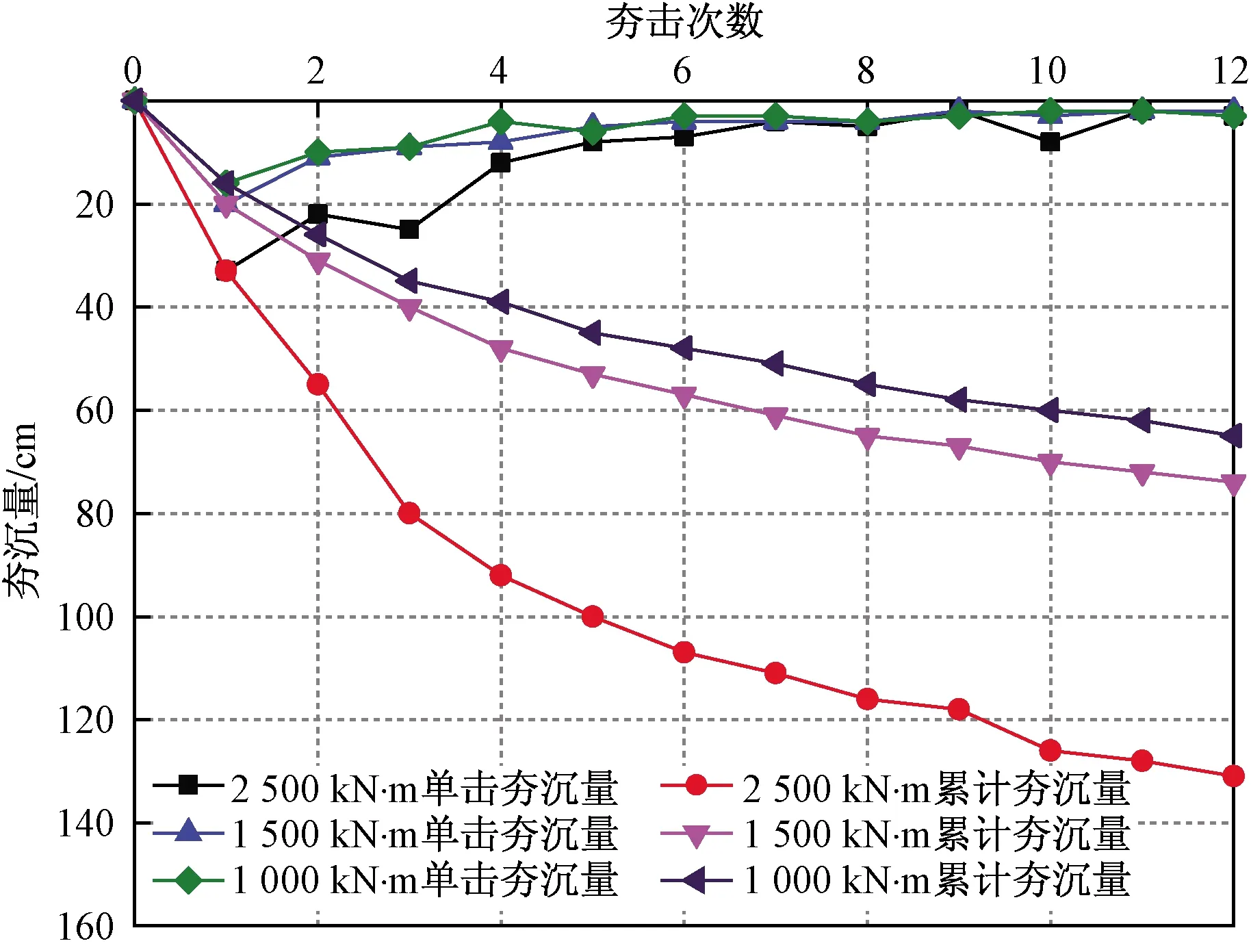
图4 夯沉量随夯击次数变化规律曲线

不同的夯击能对应不同的稳定态，夯击能越大对应的稳定态越高。夯前2-1、2-2、2-3回填土质相同，密度基本相同，则夯前夯点土体所处状态基本相同。而强夯过程中土体向更高稳定状态进化的宏观表现为夯沉量的变化，所以强夯后夯点土体趋近的稳定态越高，夯点夯沉量越大。

由表2和图4可知：不同夯击能作用下，前几击夯沉量有明显差异，后续夯击时单击夯沉量基本相同。

由式(10)可知，η与锤重M、土体密度ρ、夯锤半径r0有关，与提升高度h无关。所以2-1、2-2、2-3夯点在前几次夯击时，夯击效能系数相同。前几次夯击时，单击夯击能越大，夯击效能越大，单击夯沉量越大。随着夯击次数增加，饱和效应影响越大，系统的进化效率逐渐的减小，夯击效能系数η逐渐减小，最终趋于某一稳定值，所以后续夯击时单击夯沉量曲线基本相同。

3 结论

(1)强夯作用下土体是耗散结构，强夯过程使土体向有序和稳定状态发展，起到加固土体的目的。强夯过程中土体向稳定状态进化的宏观表现为夯沉量的变化，土体达到新的稳定状态的宏观表现为夯沉量趋近于某一稳定值。

(2)强夯过程中的夯击效能(即耗散能)等于冲击荷载所做的总功减去土体的阻尼和回弹消耗；计算得夯击效能系数η与夯击因素λ=M/ρr03有关，且对于碎石素填土λ趋于∞时，η趋于87.5%。

(3)单击夯击能相同的情况下，随着夯击次数的增加，土体的孔隙比逐渐减小，最终趋近于极限孔隙比，夯击效能系数η、单击夯击效能、单击夯沉量最终均趋近于某一个稳定值；夯击前夯点土体密度越小，前几次夯击时夯击效能系数η越大，则单击夯沉量越大，随着夯击次数的增加，饱和效应影响逐渐增大，系统的进化效率逐渐减小，最终趋于某一稳定值，则后续夯击时单击夯沉量基本相同。

(4)土质条件及密度相同的情况下，不同的夯击能对应不同的稳定态，夯击能越高稳定态越高，夯点的累计夯沉量越大。