基于降雨入渗概化模型的王家台滑坡岩土参数反演分析

张新伟，朱心广，冯春*，王心泉，刘新明

(1.北京市地质工程勘察院，北京 100048；2.中国科学院力学研究所流固耦合系统力学重点实验室，北京 100190；3.中国科学院大学工程科学学院，北京 100049)

中国是滑坡灾害的多发国家，降雨降水、地震活动、水库蓄水等因素是诱发滑坡灾害的主要原因。其中，以降雨为诱因诱发的滑坡灾害占中国滑坡灾害总量的70%～90%[1-4]。降雨型滑坡主要有3个阶段：第一阶段是在降雨降水过程中雨水持续入渗边坡体，边坡体的自重不断增加且孔隙水压力持续升高，直至破坏边坡体的极限平衡状态并产生滑动；第二阶段是由于降雨降水产生的地下水位升高软化了边坡体的潜在滑动面，并降低了边坡体的抗剪强度；第三阶段是在入渗和蒸发的反复作用下使边坡体产生了节理裂隙，从而导致了边坡体的失稳滑动[5-6]。

在降雨型滑坡中，国内外学者的主要关注点是降雨入渗分析力学模型和坡体稳定性评价方法。Hurley等[7]通过算例描述了地下水位在边坡中的时空演化规律；李宁等[8]将非饱和土视觉几何(visual geometry，VG)模型与修正后的Green-Ampt入渗模型相结合，提出了一个降雨诱发浅层滑坡的简化计算模型。陈晓东[9]将刚体极限平衡法与Mein-Larson入渗模型相结合，建立了一种降雨型边坡稳定性分析的通用分析模式；李龙起等[10]利用有PFC2D研究了竹林沟滑坡整体的失稳模式，得出在持续降雨作用下边坡中后缘表现为蠕滑-拉裂模式，应力和位移整体上从前缘到后缘呈递减趋势；雷远见等[11]通过离散元方法和强度折减法的结合，讨论了含多结构面情况下岩质边坡的稳定性。李世海等[12]采用连续-非连续单元法(continuum-discontinum element method，CDEM)，将滑坡体的地表裂缝作为分析的参数基本量，讨论了滑坡体的运动性破坏。韩廷文等[13]在考虑地下水和地震力作用下，得到降雨条件下边坡稳定性及表面水平位移变化规律。王如宾[14]等对不同工况下降雨入渗引起的滑坡堆积体的渗流稳定性进行了数值分析。田东方等[15]以 Richards 方程和有限元法为基础，通过数值算例讨论了径流补给对降雨型滑坡稳定性的影响。童欣等[16]采用有限元方法，分析了降雨入渗对含软弱夹层滑坡的稳定性的影响。叶唐进等[17]进行了降雨条件下滚石滑坡失稳机理的试验研究，推导出了适用于滚石斜坡降雨入渗条件的简步法稳定性计算公式；贺可强等[18]以弹塑性理论和损伤力学为基础，提出了降雨动力增载位移响应比的评价参数、预测模型和稳定性判据。关晓迪等[19]通过数值计算和实验方法研究了不同坡比条件下黄土边坡降雨入渗规律和机理。高谦等[20]利用GPS监测和数值模拟对干坡和降雨工况下的边坡稳定性进行了测试。王成华等[21]分析了雨强、坡角和孔隙比对非饱和砂土的非正交入渗规律。曾铃等[22]利用有限元方法对降雨型边坡的一维渗流及二维渗流过程进行了计算。熊勇林等[23]基于有限元-有限差分理论，建立了水-土-气三相渗流-变形耦合有限元数值分析。

由于地质体具有非连续、非均匀、流固耦合、未知初始状态等特点，仅依靠有限的钻孔数据无法准确给出滑坡体的渗流参数及岩土力学参数。为了准确评价降雨条件下王家台滑坡的稳定性及成灾风险，现提出一种降雨入渗坡体的概化模型，通过将该模型内嵌于连续-非连续单元法(CDEM)中，对降雨诱发的滑坡灾害进行快速模拟；借助遗传算法，通过监测数据与数值模拟耦合的优化分析，即可优选出与现场监测数据相匹配的王家台滑坡当前岩土参数。

1 降雨入渗概化模型

通常情况下，坡体的降雨计算涉及固体应力场及孔隙渗流场的耦合计算，计算过程中需要采用真实时间模拟降雨过程，数值模型的计算时步受制于模型的渗流参数、网格尺寸和总计算时长。为了精确描述坡体的流固耦合过程，重点区域的网格尺寸大都要求在米量级以下，且坡体中往往存在高渗透地层。因此，采用显式耦合算法的求解步长为秒量级甚至毫秒量级，而降雨分析的总时长往往在年量级，从而导致计算耗时巨大。

基于上述问题，提出了降雨入渗概化模型。该模型重点考虑降雨对地质体强度的影响，忽略降雨引起的渗流压力及降雨诱发入渗诱发地质体破裂对坡体稳定性的影响。该模型中需事先假定坡体的渗透层，而后将降雨量转化为可渗透地层的饱和度，当饱和度达到1后，开始对可渗透地层的强度参数(黏聚力、抗拉强度、内摩擦角)进行折减，以达到降雨弱化岩体的目的。该简化模型中仅包含固体应力场的计算，该部分计算可采用准静态算法，因此计算效率可以大幅度提高。

1.1 地质体中储水量的计算

假定地质体中的雨水流入量为外部降雨，流出量分为地表径流和地下径流(图1)。

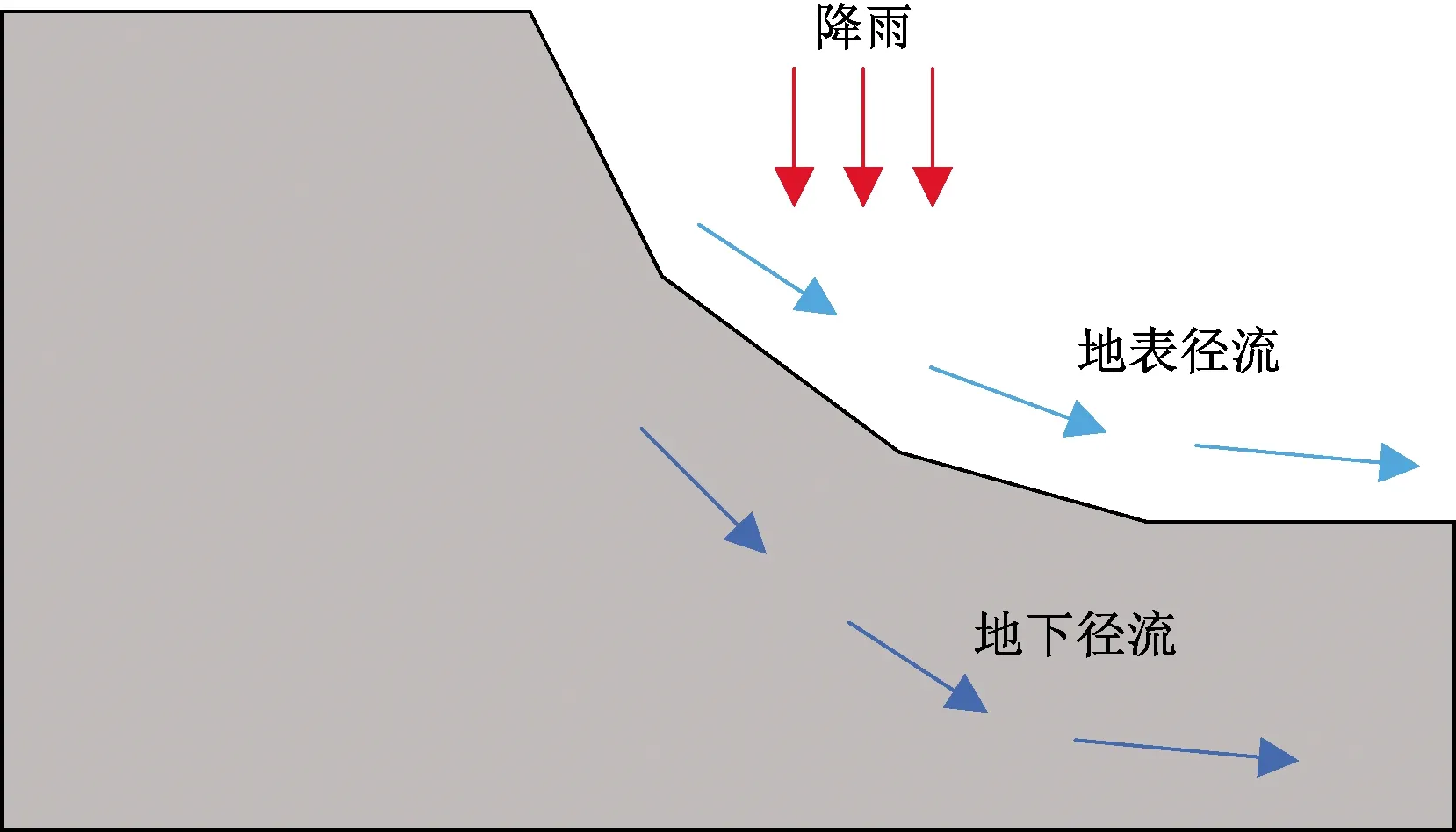
图1 降雨径流示意图

t时刻岩体中的含水量可表示为

Vt=Vt-1+ΔV

(1)

式(1)中：ΔV为t时刻岩体中雨水的增量，可表示为

ΔV=Rt-αVt-1-βVt-1

(2)

式(2)中：Rt为t时刻岩降雨量，m3/s；α为地表径流系数；β为地下径流系数。

岩体中t时刻整体饱和度定义为

(3)

式(3)中：n为岩体孔隙率，%；V为可透水岩体体积。

1.2 强度参数折减

当St=1时，开始强度参数折减，折减公式为

T=(T0-1-γDTmax)e-t1/ΔT+γDTmax

(4)

式(4)中：γD为恢复强度系数；Tmax为岩体原始强度值，Pa；T0-1为St=1时的初始时刻强度值，Pa；t1为岩体内部饱和度为1时的持续时间，s；ΔT为强度改变所对应的特征时间，s。

1.3 强度参数折减

当St=0时，开始强度参数增加，公式为

T=(T1-0-γUTmax)e-t0/ΔT+γUTmax

(5)

式(5)中：γU为恢复强度系数；T1-0为St=0时的初始时刻强度值，Pa；t0为岩体内部饱和度为0时的持续时间，s。

1.4 计算流程

降雨快速计算模型的执行流程如图2所示。

图2 降雨入渗概化模型流程图

2 遗传算法

采用遗传算法进行降雨入渗概化模型关键参数的反演优化。遗传算法利用简单的编码技术和进化繁殖机制解决复杂的多极值优化问题。

进行降雨参数识别的第一步就是定义一个目标函数，然后采用某些优化方法求解。采用的目标函数为

(6)

式(6)中：um为地表观测位移；uc为数值计算位移；α、β、n、γD、γU、ΔT为降雨参数。

采用改进型的十进制遗传算法进行动态寻优，该算法包括重组、变异、选择和精英搜索4个步骤。

步骤1重组。重组是最主要的遗传运算，它同时对两个个体操作，组合二者的特性产生新的后代。采用如下所示的凸交叉，在种群中随机选择两个个体xα和xβ，经过交叉后产生两个新个体，表达式为

(7)

式(7)中：μ为服从[0，1]的均匀分布。

步骤2变异。变异是另一种最基本的运算，它在种群中个体上自发地产生随机的变化。一种简单的变异方法是随机替换一个或多个个体。在遗传算法中，变异可以提供初始值其中不含有的个体，或找回在重组和选择中丢失的个体，为种群提供多样性。

(8)

步骤3选择。选择的作用是优胜劣汰、适者生存。将多个个体值代入式(6)，将值最大的个体淘汰。

步骤4精英搜索。将较差的个体淘汰后剩下的即为精英个体，可进行下一轮的遗传算法寻优。

3 王家台滑坡的地质特征

王家台滑坡位于北京市房山区霞云岭乡王家台村西南方向130 m左右处(图3)。所属地质灾害类型为不稳定斜坡，长约143 m，宽为30～50 m，面积约6 000 m2，坡高约50 m，坡度约40°，分布高程516～531 m。地势为西部高，东部低。

图3 王家台滑坡航拍图(1∶1 300)

不稳定斜坡西部植被覆盖一般，主要以灌木为主，植被覆盖率约60%。斜坡东部呈阶梯状，平台与平台之间为近直立的陡坎，平台处种有玉米、南瓜和大树。每个陡坎处均砌有高1.0～2.5 m的干砌石挡土墙，大约有20级，结构松散、无定向性。斜坡底部为108国道，一旦发生滑塌，将会危及108国道。

该滑坡周边出露地层为上元古界蓟县系、更新统坡洪积物(Qp3dpl)和全新统冲洪堆积物(Qhapl)，岩层产状变化不大。大部分山体坡面较为稳定。沉积物为砾石、砂、砂质黏土、亚砂土，以前两者为主。区域大地构造位置处于华北板块中部，燕山台褶带中的次一级构造单元西山迭拗褶带西部。区域地质构造复杂，处于后吕梁-印支期地台盖层褶皱中的第二亚构造层，其西北部有一条张剪性断裂，东南部位有一条推覆构造。

据斜坡的现状空间几何特征、物质组成及所处的地质环境分析，不稳定斜坡坡体破坏形式主要为滑塌，斜坡主要成分是第四系人工梯田和坡积碎石覆盖于青白口系下马岭组(QNx)泥质粉砂岩之上，斜坡因开挖形成陡坎，并且斜坡整体植被保持水土能力较差，如遇暴雨天气，斜坡土体受雨水侵蚀，易发生滑塌。斜坡主要影响因素包括内部条件和外部条件两类，内部条件包括地形地貌、坡体结构；外部条件包括降雨、风化、地震、人类工程活动等。

4 数值模型与计算工况

4.1 数值模型

建立如图4所示的王家台数值计算模型。模型后缘高度67 m，前缘高度30 m，西向长度76 m，北向长度115 m。模型共包含两类地层，其中基岩为泥质粉砂岩，覆岩为破碎积石。前缘坡脚处为108国道。1-1′、2-2′、3-3′为截取的3个横截面。

4.2 计算工况及参数

反演目标是王家台滑坡的岩土参数，具体包括地表径流系数、地下径流系数、岩体孔隙率、残余强度系数、恢复强度系数、强度变化特征时间；收敛条件是0092及0093两个地表位移监测点(图4)的实测曲线与数值模拟曲线的误差小于20%。

图4 王家台滑坡地质模型

在2019年3月—2020年7月王家台滑坡降雨观测站记录的460 d降雨数据如图5所示。

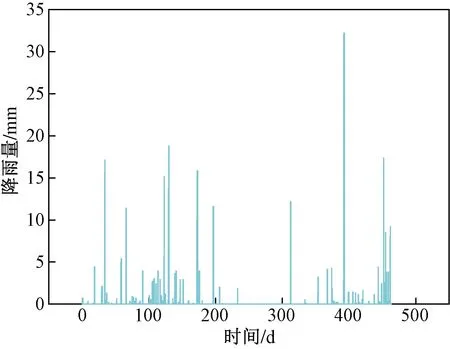
图5 王家台滑坡降雨数据

地层基本参数如表1所示。

表1 王家台滑坡地层基本参数

4.3 正常工况(非降雨)下安全系数计算

如图6所示，截取图4中3个横截面，利用GDEM软件进行非降雨工况下王家台滑坡灾害点的安全系数分析。图7所示为塑性剪应变云图，针对截面1-1′，塑性区域位于地层分界处，处于边坡中部坡度较陡处，边坡安全系数为1.46；截面2-2′中存在边坡上部与边坡中部两个塑性区，边坡安全系数为1.682；截面3-3′的塑性区位置与截面2-2′相同，安全系数为1.45。塑性区所在位置处为潜在滑动危险区，结合3个截面计算情况，王家台滑坡灾害点综合安全系数为1.53，现场监测安全系数为1.50，计算误差2%。

图6 王家台剖面图

图7 塑性剪应变云图

4.4 降雨工况下参数反演计算结果

基于提出的降雨入渗概化模型，以现场监测得出的0092和0093两个监测点的地表位移曲线为优化目标，结合遗传算法进行动态调参，最终数值计算得出的位移曲线和现场数据对比曲线如图8所示。

图8 现场监测与数值计算位移曲线对比图

分析曲线可知，0092测点上升期(前150 d)数值计算结果相比监测结果偏低，后期与监测结果基本一致。0093测点上升期(前150 d)数值计算结果与监测结果吻合较好，后期相比监测结果略偏大。总体而言，数值计算结果与现场监测结果总体趋势一致，吻合较好，这也说明了提出的降雨入渗概化模型的合理性和有效性。

在给定的初始岩土参数，结合降雨入渗概化模型和遗传算法进行王家台滑坡当前岩土参数的寻优计算；最终给出与降雨入渗概化模型相匹配的岩土参数：地表径流系数α=0.1，地下径流系数β=0.05，岩体孔隙率n=0.01，残余强度系数γD=0.2，恢复强度系数γU=0.8，强度改变系数所对应的时间ΔT=5×106s。

5 结论

(1)提出了可快速分析降雨入渗诱发滑坡灾害的力学模型。该模型根据降雨量、地表径流量及地下径流量综合确定滑体中的饱和程度，进而根据饱和度来折减或增加滑体的强度。由于不需要进行渗流应力耦合的计算，因此可大幅提升计算效率。

(2)运用GDEM软件，截取王家台滑坡灾害点特定剖面进行正常工况下安全系数分析，得出综合安全系数为1.53，相比于现场监测误差为2%。

(3)基于提出的降雨入渗概化模型，结合遗传算法，实现了王家台滑坡岩土参数的反演分析。经过监测数据与数值模拟的优化对比，给出了适用于降雨入渗概化模型的王家台滑坡当前岩土参数为：地表径流系数α=0.1，地下径流系数β=0.05，岩体孔隙率n=0.01，残余强度系数γD=0.2，恢复强度系数γU=0.8，强度改变系数所对应的时间ΔT=5×106s。基于上述参数，可进一步开展王家台滑坡在不同降雨条件下的成灾风险分析。