自主移动机器人动态避障轨迹规划方法

邱少林

(安徽博研信息科技有限公司，安徽 芜湖 241000)

自主移动机器人作为机器人领域的热门研究对象，正在引起极大的关注。移动机器人可应用于仓储物流、医疗、服务等多个领域[1]，但通常需要面临复杂的工作环境，在这些场景中，移动机器人需要规划出一条连接起点和目标点的连续无碰撞轨迹，被称为轨迹规划问题[2-3]。

先进的轨迹规划方法是移动机器人领域研究的关键技术[4]，不同于路径规划[5]，轨迹规划需要考虑路径约束、环境无碰撞约束以及机器人运动学约束等约束与要求，根据路径与约束，生成一系列包含位置和速度信息的位姿序列，使机器人从起始位姿安全运动到目标位姿。在无法获得完整环境信息或者环境中存在动态障碍物时，移动机器人需要对环境变化做出实时反应[6]。

本文提出一种基于时间弹性带的速度求解与避障联合机制的轨迹规划方法，应用于阿克曼结构的类车机器人。考虑并优化TEB 多种约束条件，保证类车机器人在动态环境下具有紧急避障能力。建立工作空间势场求解机器人速度，提高运动舒适性。分别在静态和动态环境下进行仿真实验，分析该方法的优越性。

1 TEB 算法

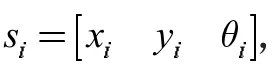
最终轨迹由位姿信息与时间间隔信息组成，表示为：

TEB 通过最小化目标函数得到最优轨迹，其中 γn是约束函数的权重系数，f(P)是各个约束目标函数之和。约束目标函数将在下文提出。最终TEB 算法优化结果为：

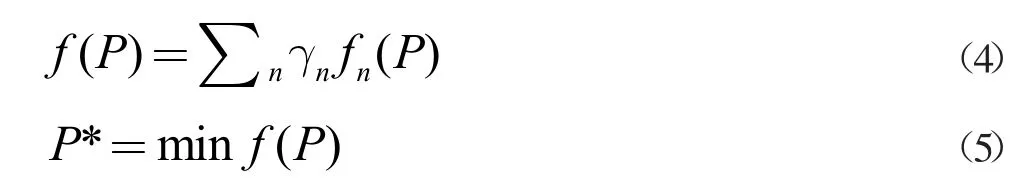
2 速度求解

建立工作空间势场U，规划机器人速度。工作空间势场由目标点吸引势场U1，障碍物排斥势场U2以及动态障碍物势场U3组成。基于工作空间势场，建立求解机器人速度的函数：

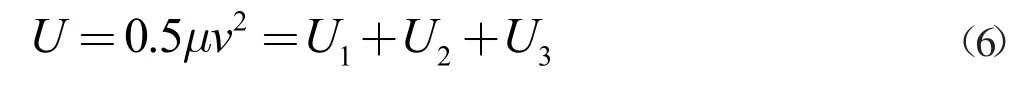
其中，μ 是速度-势场转换系数，v 是速度。

3 约束目标

目前，还需要对移动机器人加速度a 和转向角α(t)进行实时控制：u(t) =[a, α(t)]。移动机器人实时运动状态由式(7)表示，β (t)是机器人后轴中心转向角度，L 为机器人轴距。

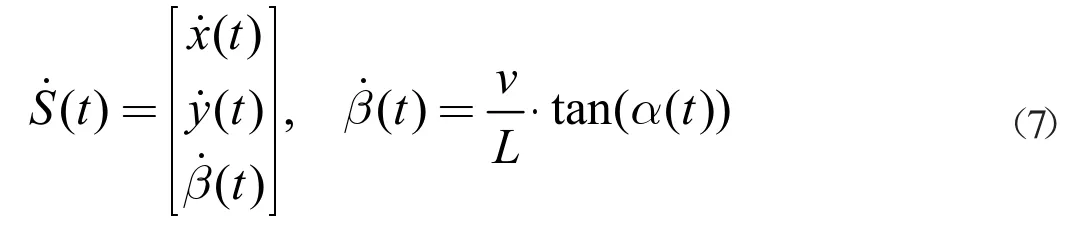
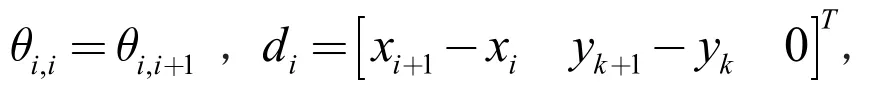
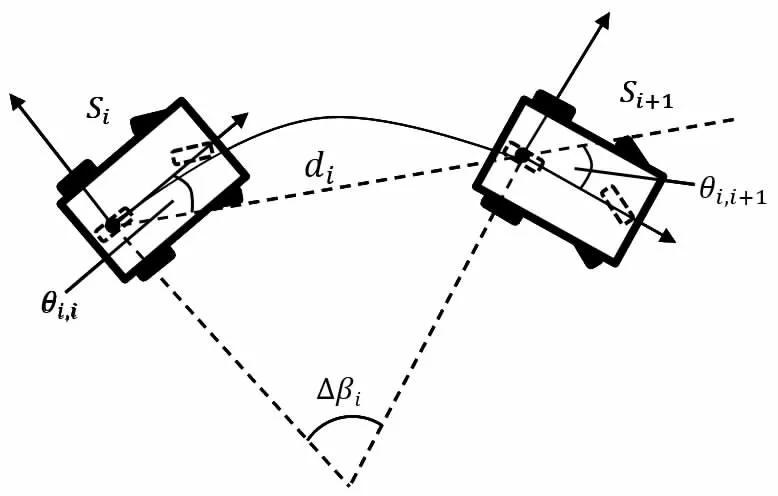
图1 移动机器人转向示意图

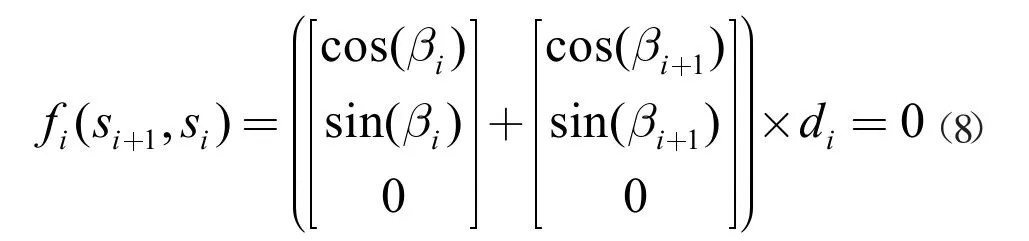
通过移动机器人自身传感器确定障碍物的位置，位置信息不断更新。引入障碍物约束函数：

时间最优要求所有位姿之间的时间间隔尽量最小化，以最短的时间到达目标点，提高效率。时间最优约束为：

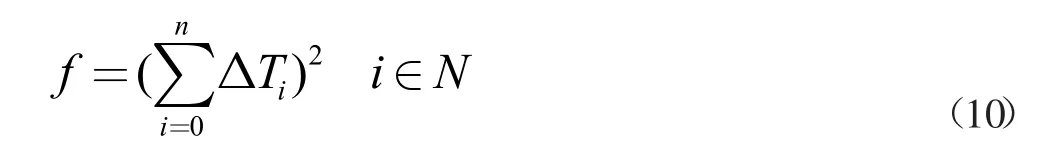
在任何时刻的转弯半径R(t)不能小于最小转弯半径Rmin。转弯半径约束为：

为使机器人到达目标点时速度为0，设置目标点加速度约束：

4 实验分析

本节为验证所提方法的有效性并测试其在特殊方面的优越性，分别进行静态实验和有动态障碍物的动态试验。

如图2 所示，静态场景实验结果表明，NTEB 可以规划出合理的运动轨迹，而且对速度的控制具有良好的运动舒适性，相比于TEB 整体运动时间缩短30%，速度相对变化减少50%。表明NTEB 运动规划方法具有更好的稳定性，同时提升了移动机器人运动效率。

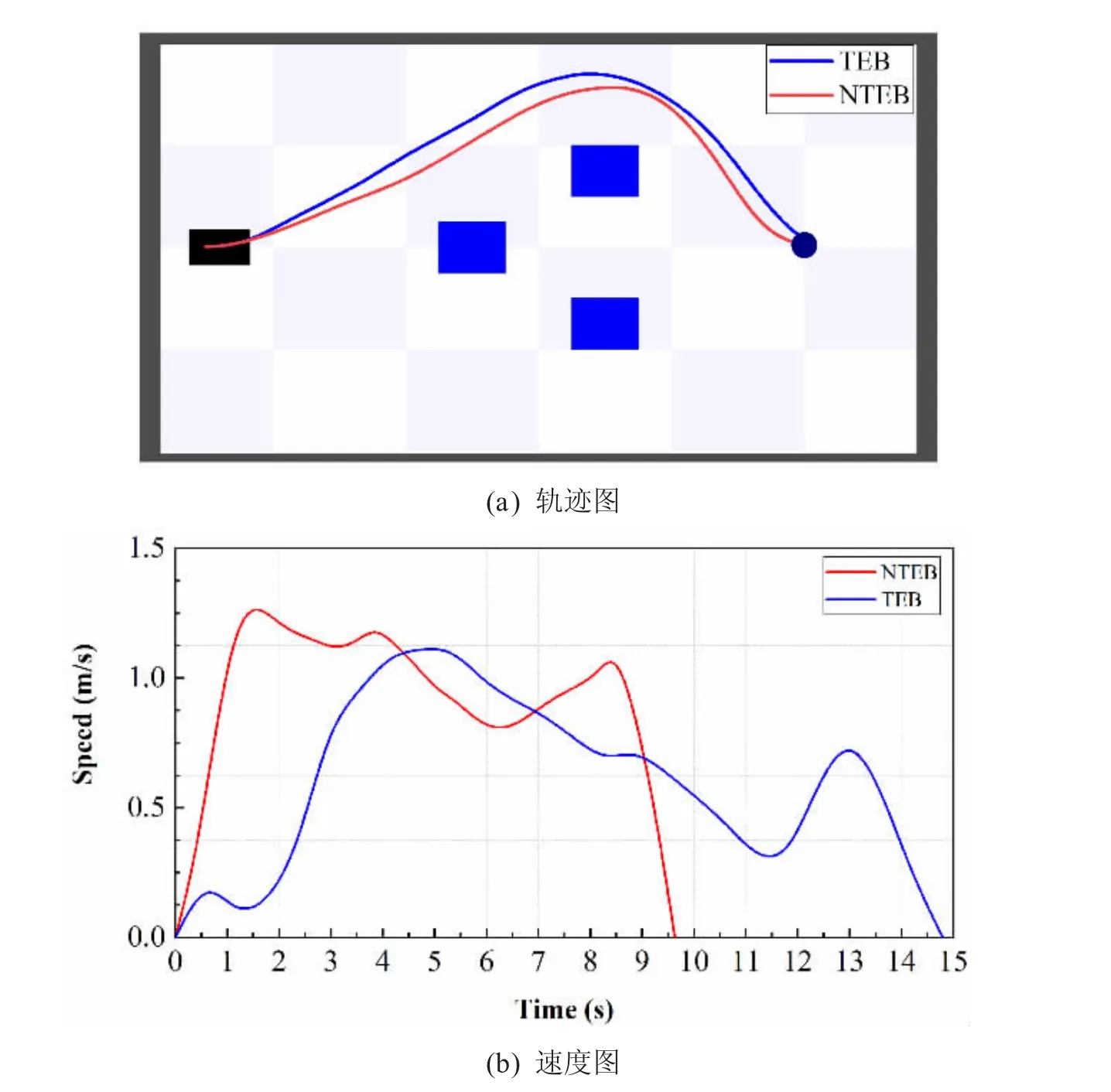
图2 静态场景实验结果

如图3 所示，动态场景实验证实了NTEB 在动态避障方面的效果，所建立的代价地图检测区域有效执行了应对动态障碍物的避障策略，确保机器人在紧急情况下具有相应的应急处置能力，尤其在动态障碍物初始时刻不可见的情况，移动机器人依然安全平稳运行，提高运动安全性。

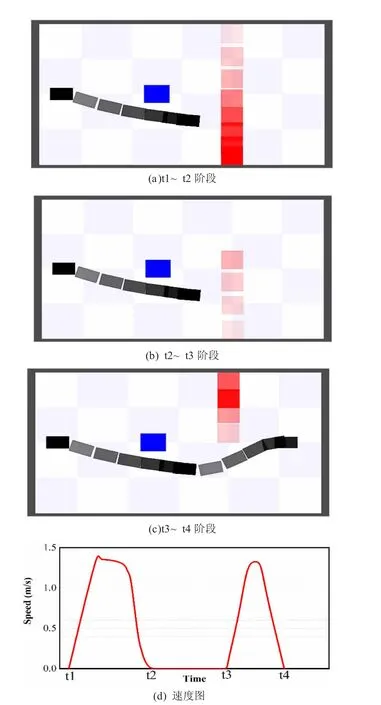
图3 动态场景实验结果

5 结论

本文提出一种基于时间弹性带的轨迹规划方法，用于求解移动机器人动态避障问题。轨迹规划需要考虑环境中不确定障碍等因素，因此该方法包含机器人运动速度、运动状态、障碍物等多种约束条件。结合多种约束条件，完成从起始点到目标点的无碰撞轨迹规划，移动机器人实现平稳无碰撞运动。实验结果表明，该方法具有优越的运动学特性和良好的避障规划效果。