一类带有多时滞的中立型奇异马尔科夫跳变系统的随机稳定性研究

龙少华 周丽娟

(重庆理工大学 理学院，重庆 400054)

1 概述

随着人类社会的进步和现代控制理论不断深入的发展，在包括航空航天、化学工程、网络、电力和经济等在内的诸多领域中，人们发现了广义系统的许多应用实例，如动态投入产出模型、纽曼模型、受限机器人模型以及核反应堆模型等。近几十年来,广义系统一直是学术界研究的热点领域[1-3]。

另一方面，时滞是自然界中广泛存在的一种物理现象。从工程技术、物理、化学反应、生物医学等领域中提出的数学模型常常带有明显的滞后量。例如，在远程控制系统中，计算机网络传输诱导的信息延迟使得系统经常出现信息滞后现象。在实际工程系统中，由于元器件老化、测量滞后等原因，在其运行过程中也常常存在滞后现象。因此，时滞系统也一直是学术界研究的热点领域[1-4]。

此外，有些实际系统，在描述其数学模型时，我们不仅需要考虑状态向量的时滞，还需要考虑状态向量的导向量的时滞，即时滞不仅存在于状态向量中，还存在于状态向量的导向量中。我们把这种系统称为中立型系统。中立型系统是一类非常重要的时滞系统，它有着广泛的应用背景，如部分元等效电路系统、无损耗传输系统、热交换器系统等。近几十年来，对中立型系统的研究也得到了飞速的发展[5-9]。

目前，对于带有多时滞的中立型奇异马尔科夫跳变系统的随机稳定性的研究还不完善。

本文将对一类带有多时滞的中立型奇异马尔科夫跳变系统的随机稳定性进行研究。

2 准备知识

在本文中，我们考虑一类多时滞的中立型奇异马尔科夫跳变系统的随机稳定性，系统的模型如下：

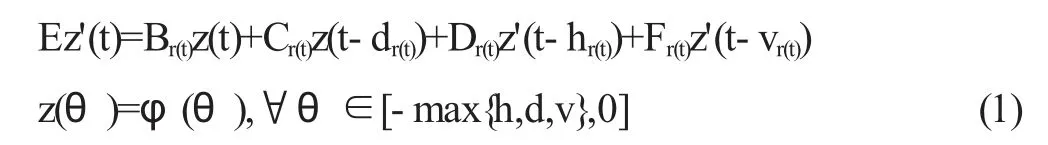
其中z(t)是n 维列向量，代表系统的状态向量。{r(t),t≥0}是右连续的马尔科夫过程，它的状态为有限个且假定其取值于集合χ={1,2, ,N}。此外，我们假定从状态i 到状态j 的转移速率bij满足下式：

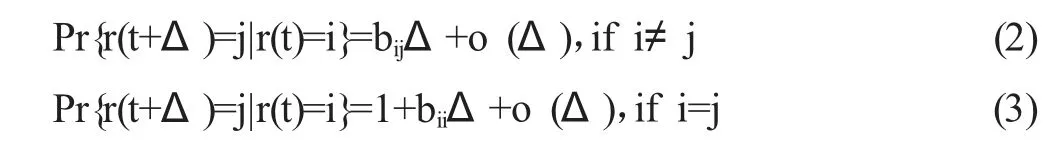
其中bij＞0(i≠j)和bii=-bi1-bi2-...-biN。

在(1)式中，hj＞0(j∈χ)，dj＞0(j∈χ)和vj＞0(j∈χ)表示系统的 时 滞 且 都 是 常 数，h=max {h1,h2,...,hN}，d=max{d1,d2,...,dN}，v=max{v1,v2,...,vN}。矩阵E、Bj＞0(j∈χ)、Cj＞0(j∈χ)、Dj＞0(j∈χ)和Fj＞0(j∈χ)都是已知的n×n 矩阵。我们假定矩阵E 的秩为m。

在后面，我们将把系统(1)转化成带有时滞的的奇异马尔科夫跳变系统。为了方便后面的讨论，我们先给出一些有关奇异马尔科夫跳变系统的定义。

定义1[3]：称系统Ez′(t)=Br(t)z(t)+Cr(t)z(t-dr(t))是正则的，如果对于每一个i∈χ，都有det(sE-Bi)不恒等于0。

定义2[3]：称系统Ez′(t)=Br(t)z(t)+Cr(t)z(t-dr(t))是无脉冲的，如果对于每一个i∈χ，都有deg(det(sE-Bi))=rank(E)。

定义3：称系统Ez′(t)=Br(t)z(t)+Cr(t)z(t-dr(t))是随机稳定的，如果对于任意的初始条件(r(0),φ(·))，系统的解z(t)满足

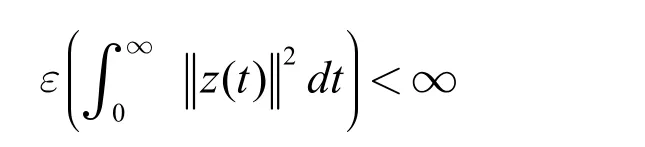
3 主要结果

在本文中，我们考虑如下情形：对于每一个i∈χ，总存在矩阵Wi和Hi分别满足

WiE=Di和HiE=Fi。

对于系统(1)，我们可得如下的定理。

定理1. 给定n×n 矩阵K 满足KE=0 和rank(K)=n-m。称系统(1)是随机稳定的，如果存在矩阵Q1＞0，M1＞0，Y1＞0，Pi＞0(i∈χ)，U1＞0 和Si(i∈χ)满足

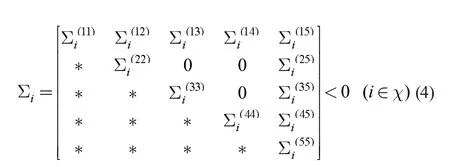
其中

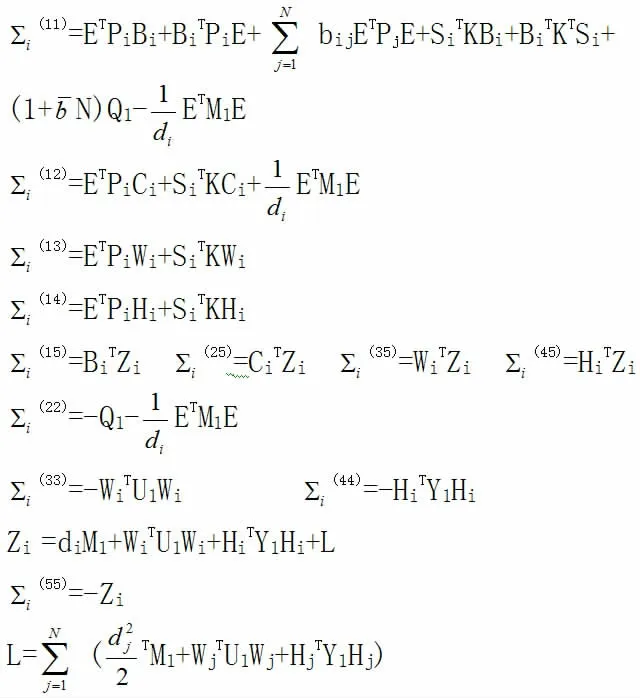
证明：我们首先证明系统(1)是正则和无脉冲的。

根据(4)式,我们可得

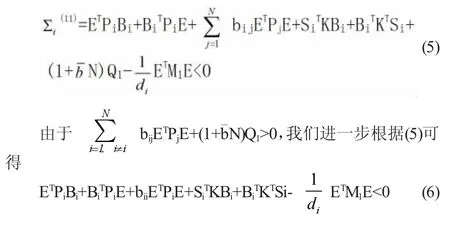
注意rank(E)=m＜n, 我们可以找到两个矩阵G1和G2满足

定义

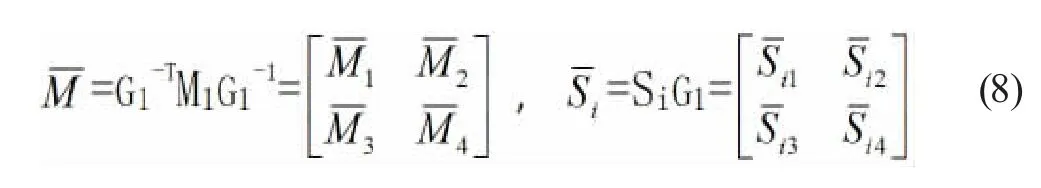
用G1T和G1分别左乘和右乘(6)式，我们可得

注意到WiE=Di和HiE=Fi，令γ(t)=Ez′(t)，可得系统(1)等价于下面的系统：

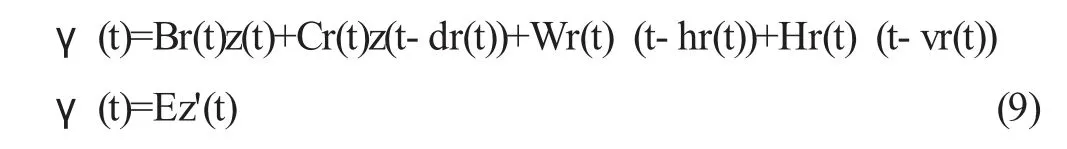
可以看出，系统(8)等价于下面的系统：

我们利用下面的李雅普诺夫泛函来帮助我们证明上述系统是随机稳定的。

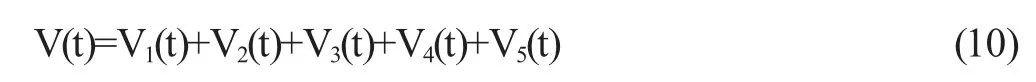
其中

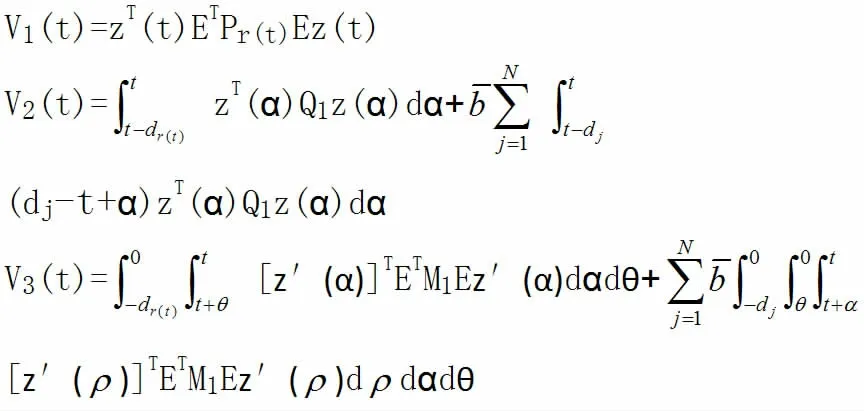
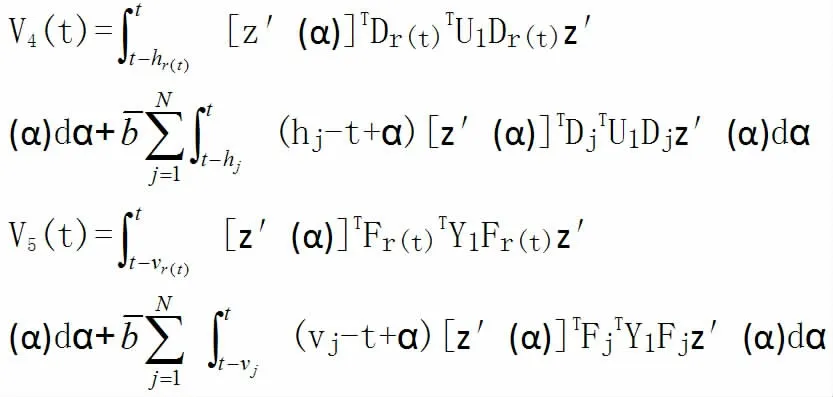
由上式我们可得

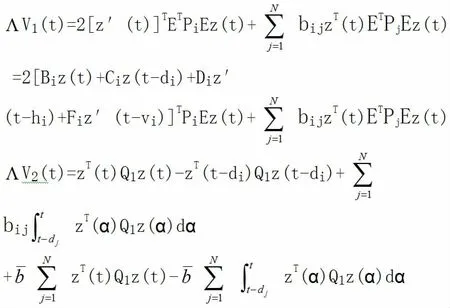
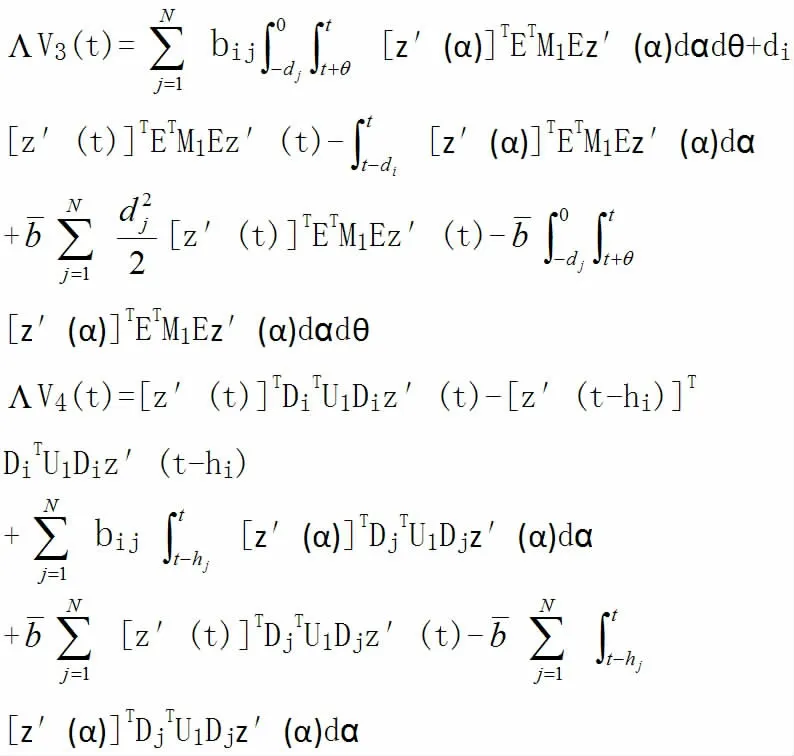
注意KE=0，我们可得2[Ez′(t)]TKTSiz(t)=0，也就是

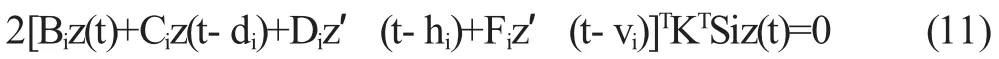
根据(10)-(11) ,我们可得

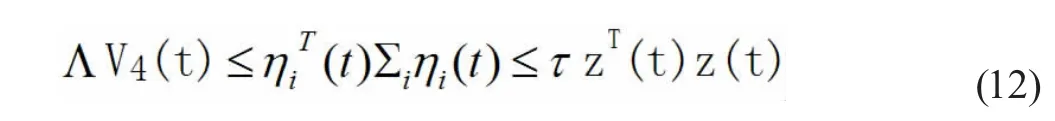
其中

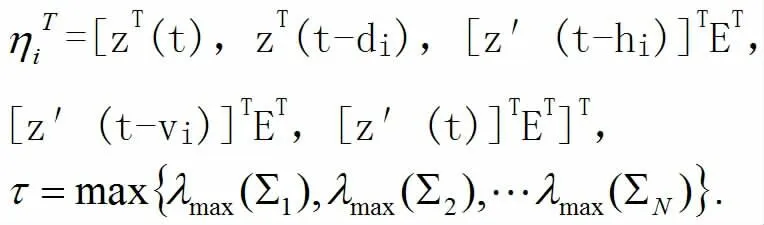
注意τ＜0，由(11)可得

所以，根据定义3 可得系统(1)是随机稳定的。证毕。

4 算例

考虑系统(1)，假定系统中的参数如下：

利用Matlab 线性矩阵不等式工具箱,我们可得线性矩阵不等式(3)是可行的。这说明了系统(1)是正则、无脉冲且随机稳定的。