气控软体驱动器结构分析与优化设计*

刘卓群，张 翔，黄奕勇，陈小前，赵 勇

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2. 军事科学院 国防科技创新研究院， 北京 100071)

复杂环境下的救援工作、生物医学诊断及手术、未来空间在轨服务以及未来家庭的人机交互等应用场景下，传统刚性机器人发挥受限，需要具备一定柔性、在发生碰撞时能保证目标安全的软体机器人[1]。软体机器人凭借其柔性、轻质及安全接触等优点，近年来发展迅速。软体机器人的发展不仅需要材料的创新，同时还要进行与之相适应的结构设计，以实现相应的大变形等控制策略。

采用不同驱动方式，软体机器人的设计与特性将出现显著差异。当前，气压驱动与线驱动是两种最普遍的驱动方式。张润玺[2]提出了线驱动软体手术机器人的形状感知控制算法，制作原理样机并成功在活体生物上进行实验。Chen等[3-4]设计了一种由充气波纹管组成的可折叠空间软体机械臂，制作了地面原理样机并进行了实验。Voisembert等[5]设计了一款通过截止栓和绳索的联合驱动实现运动控制的充气机械臂。两种驱动方式的差异主要体现在软体机器人的运动灵活度、对控制的响应速度以及末端负载能力三个方面。

对气压驱动方式而言，不同结构的气控软体驱动器运动性能和力学性能差异很大。其中，气囊的设计和研究属于关键环节。传统气囊结构分为密闭型气囊、排气型气囊和组合型气囊[6]，本文研究的气控软体驱动器属于密闭型气囊。对气囊的设计研究可分为解析法、有限元仿真法以及实验法。其中，有限元仿真法不需要引入过多假设条件，也不受气囊大变形影响，且仿真成本相对较低，为国内外大多数学者所采用。Lee等[7]通过有限元分析，利用LS-DYNA对“猎户座”乘员舱着陆气囊进行结构优化设计，成功降低整体着陆载荷，提升了乘员舱的整体稳定性。

气控软体驱动器的性能指标与驱动器的每一项设计参数都息息相关，为提升气控软体驱动器的整体性能，需要先对驱动器进行参数化建模，对参数进行灵敏度分析确定高灵敏度参数，然后采用相应的优化算法对目标进行优化。在模型参数化研究方面，李晓祥等[8]通过将试验载荷参数化，解决了传动实验台在非平稳实验条件下的载荷表达问题；李治宇等[9]通过VB编程结合SolidWorks完成了对Clipper返回舱的参数化建模；秦宇等[10]利用Python脚本对ABAQUS进行二次开发，完成了对优化目标的参数化建模；陈红伦等[11]通过解析钢筋模型的几何信息，通过程序生成基于IFC标准的钢筋参数化模型；李忠献[12]、赵昕[13]、孙立镌[14]等分别对不同系统的模型参数化方法进行了改进。建立参数化模型后，需要进行多参数灵敏度分析，统计不同参数对目标性能的影响程度。文献[15-18]采用单参数变化方法、正交试验设计结合方差分析或基于深度神经网络等不同方法进行了参数敏感性分析；尹汉锋等[19]采用遗传算法结合LS-DYNA对气囊排气孔径等参数进行了优化设计；刘鑫等[20]采用多目标遗传算法结合气体热力学性质，完成了气囊动态特性参数优化。

在目前的气控软体驱动器的研究方面，王华[21]、许宗贵[22]等建立了气控软体驱动器的数学模型，分别通过有限元仿真和实验测试的方法验证了数学模型的有效性。谢荣臻等[23]建立气控软体驱动器的数学模型，采用解析法建立单目标多约束优化模型寻找最优尺寸参数组合，完成了对气控软体驱动器的设计优化，提升了其弯曲性能。刘春山[24]对SMA人工肌肉进行了建模分析研究，通过实验测试的方法获得了驱动辐射对称型软体机器人的最优参数。综上，学者们进行仿真分析时主要通过将Cad模型导入ABAQUS等有限元软件或直接手动建立仿真模型进行分析，若参数变化，则需要手动修改模型，不利于提高计算效率。在对气控软体驱动器进行优化分析时，主要通过建立数学模型，用数学解析的方法得到优化函数，然后进行寻优计算。此种方法对数学模型精度要求较高，若数学模型不够精确将直接导致优化结果的偏差。若采用实验法，制作实验样机分批测试，该方法能最直接准确地反映出优化结果的合理性，但该方法成本较高，不具有普适性。

气控软体驱动器是软体机械臂的重要结构组件，本文针对现有驱动器倾角和支反力有限的问题，提出气控软体驱动器的智能优化设计方法。

1 模型参数化

1.1 几何模型与物理过程描述

气控驱动器由三个完全相同的波纹管气囊对称并联，波纹管气囊之间通过一系列薄板连接。整体设计如图1所示，剖面构型及充气方式如图2所示。波纹管气囊在充入不同气压时，将呈现不同的长度变化，通过波纹管气囊与薄板的联合作用，可实现驱动器整体的弯曲指向运动。

图1 气控驱动器设计图Fig.1 Schematic diagram of pneumatic manipulator

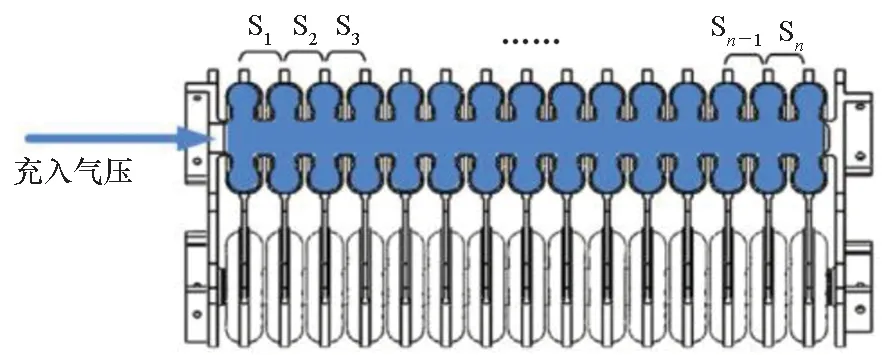
图2 气控驱动器剖面Fig.2 Section view of pneumatic manipulator

1.2 结构参数化

结构优化主要分为参数优化和无参优化两类。参数优化是通过参数化手段研究结构尺寸及工艺参数等对目标量的响应，获得因子的影响规律和最优解集；无参优化则以刚度最大、质量最小等作为目标量，进行拓扑或者形貌优化，通常会极大地改变结构形状。气控驱动器的变形优化属于参数优化，在结构参数化时需控制每一个特征尺寸，通过垂直、相切、平行、相等、固定等方式进行尺寸约束，避免出现相交、错位、重叠等结构错误，下面对结构参数化过程进行详细描述。

1.2.1 气囊

取气囊最小特征结构进行参数化，尺寸名称和标注如图3所示，其中r1和r2为所指圆弧段的半径。在进行结构优化时，每一个尺寸均为独立变量。

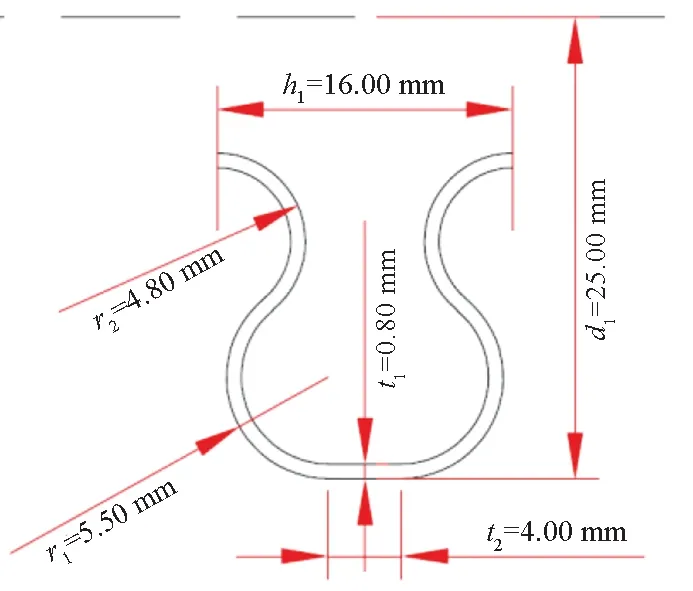
图3 气囊最小特征结构参数化图Fig.3 Parameterized diagram of the minimum characteristic structure of the airbag

1.2.2 薄板

去除掉其中部分圆孔和圆角等非关键部位结构，参数化尺寸名称和标注如图4和图5所示，其中r6为所指圆弧段的半径。在进行结构优化时，r3(r3=d1)、r4(r4=r3+2)及t4(t4=t2)为非独立变量，其余尺寸均为独立变量。

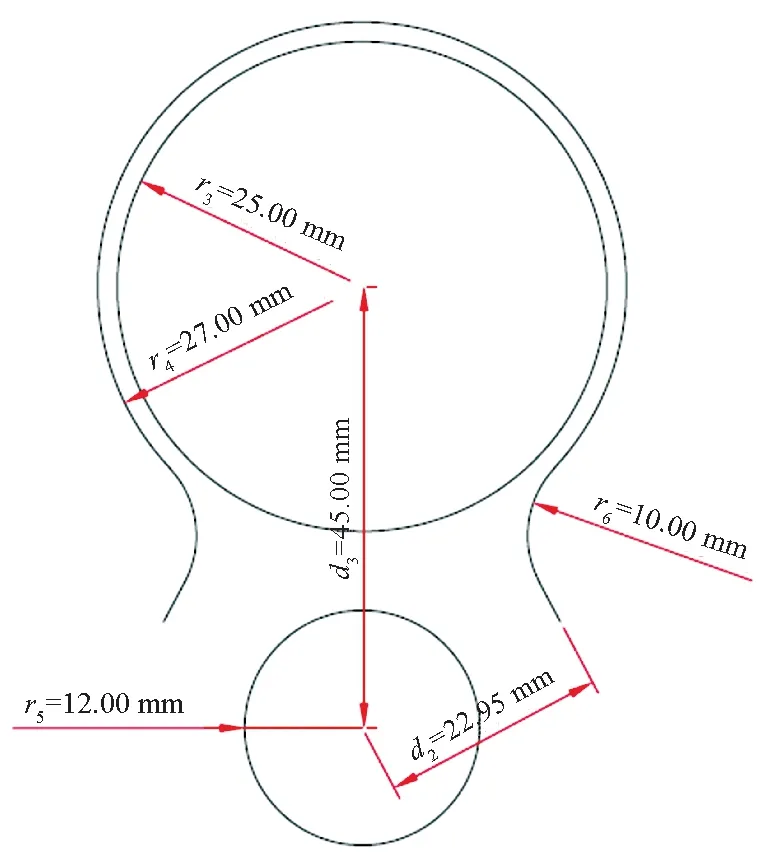
图4 薄板最小特征结构参数化平面图Fig.4 Parameterized plan of the smallest characteristic structure of the thin plate

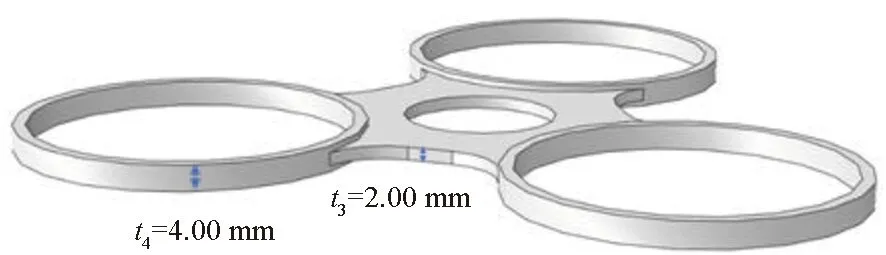
图5 薄板最小特征结构参数化立体图Fig.5 Parametric stereogram of minimum characteristic structure of the thin plate

图4和图5中的“最小特征结构”是指几何模型中的最小重复结构，可由它通过阵列或复制等操作实现几何建模。

2 结构分析与优化设计方法

2.1 结构分析方法

采用有限元仿真法对气控驱动器的充压变形过程进行仿真分析，通过Python语言对ABAQUS二次开发，完成了仿真过程中的前处理建模(仿真建模、边界、载荷、时间步、物理场设置)以及后处理(可视化、计算结果处理、数据提取)过程。下面就其流程进行详细说明。

2.1.1 仿真建模

基于Python脚本接口的参数化建模易于修改模型的几何结构参数，便于模型执行有限元分析。采用Python语言开发脚本，建立气控驱动器参数化模型，由二维草绘生成一个三维旋转体——气囊，最终建立气控驱动器仿真模型。为优化效率和计算量考虑，根据几何、载荷、边界的对称性，实际仿真时只取半模型进行计算。

在实现上述参数化建模时，需要注意结构间的尺寸约束关系：一部分尺寸约束是气控驱动器结构具有的内在特征，可视为结构造型；而另一部分是为避免干涉等结构错误施加的，可视为优化约束。为利于优化分析，需在程序中对这两类约束实行自动化控制。

2.1.2 网格划分与载荷设置

出于计算精度和计算量的综合考虑，需要对四面体单元和六面体单元进行比较。根据有限元理论和力学理论可知，一阶四面体单元为常应力应变单元；六面体单元形函数含有非一次项，具有更高的精度。但一阶六面体单元存在天然的缺陷，在外力作用下可能会出现“剪力自锁”或“沙漏”现象，这两种现象都有可能导致结果错误。为降低影响，一方面，可以细化网格，增加网格数量；另一方面，可以换用二阶单元，从本质上去除“剪力自锁”与“沙漏”现象的影响。但这两种改善网格性能的方式均会增加计算量，而由于气控软体驱动器结构优化过程计算量较大，显然六面体单元并非明智选择，所以在不牺牲计算精度的同时，为提高计算效率与有限元模型的收敛性，在此选择C3D4四面体单元进行网格划分。

气控驱动器的充压变形结构优化过程基于两个载荷工况进行。

1)载荷工况一：驱动器底部固定，一个气囊充压，实现弯曲变形，统计弯曲倾角(如图6所示)。

图6 弯曲倾角示意Fig.6 Schematic diagram of bending inclination

2)载荷工况二：驱动器两端同时固定，一个气囊充压，主要实现内部挤压，统计顶部支反力。

加载情况如图7所示，压力最终以剪力形式作用在气囊内表面，从而产生定向弯曲。

图7 气控驱动器充气加载示意Fig.7 Schematic diagram of internal inflation pressure of pneumatic manipulator

2.1.3 求解器选择

在有限元数值计算中，隐式计算采用Newton-Raphson增量迭代法，在计算精度方面具有较大优势；显式算法采用中心差分，本质上是一种线性插值，牺牲部分数值精度，需要通过减小时间步长弥补。在计算量方面，两种算法不能进行绝对比较，因为隐式算法采用迭代方法，计算量取决于收敛程度；而显式算法由于采用线性化处理，且为了考虑应力波传递和可能的共振行为，要求时间步长极小，所以计算量通常较大。

两种算法各有优劣，实际仿真中通常结合具体物理过程选择。出于对优化过程连续性和计算量的考虑，隐式算法容易出现不收敛而使计算中断，对优化迭代极其不利；但同时，显式算法一般适用于高速冲击过程，如果为了达到准静态过程而一味地延长加载时间，将极大增加计算量。经计算评估，在气控驱动器充压变形过程中，显式算法计算量远大于隐式，因此本文选用隐式算法进行结构优化仿真。

2.2 优化设计方法

2.2.1 优化方法

在Isight软件中，优化算法大致分为三大类，分别为数值优化算法、直接搜索优化算法和全局探索优化算法。其中全局探索优化算法可以处理多峰性、非线性、非连续、不可微等问题，并进行全局寻优。气控驱动器结构优化过程涉及的优化变量多，约束条件复杂，同时仿真计算又选用隐式迭代算法，可以预见，目标函数会出现多峰性、非线性、非连续、不可微等问题，因此决定选用全局探索优化算法中的进化优化算法(Evolutionary optimization algorithm, Evol)进行优化。

Evol是通过在每个设计变量上增加一个正态分布的随机值来突变设计，正态分布的期望和标准差是自适应的，在优化过程中会发生变化。该算法可以一次性改变多个设计变量，并能保证设计点不重复，还可以同时并行计算多个设计点，选出最优设计点指向下一步，特别适合于严重非线性、不连续、计算量巨大的优化进程。

2.2.2 优化思路

如前所述，气控驱动器的充压变形结构优化涉及两个载荷工况，优化目标为同时使弯曲倾角和支反力最大。涉及多目标优化时，不同目标间具有较强的耦合关系，优化难度较大。为此，应作加权和归一化处理，将多目标耦合为一个目标进行优化。具体思路如下：①弯曲倾角作为单一优化目标获得其最大值Amax，如图8(a)所示；②支反力作为单一优化目标获得其最大值Fmax，如图8(b)所示；③将弯曲倾角与支反力作为多目标优化时，分别以Amax值和Fmax值为分母作归一化处理，目标加权比为1 ∶1，如图9所示。

(a) 倾角(a) Inclination angle (b) 支反力(b) Reaction force图8 倾角与支反力单目标优化示意Fig.8 Schematic diagram of single objective optimization of inclination angle and reaction force

在图例中，有Optimization、Simcode及Calculator三个组件。Optimization执行优化设计，图8(a)中Angle、图8(b)中Reaction、图9中Angle_Reaction为优化组件；优化组件通过调用Isight算法库的Evol优化算法，在每次优化开始前，在d1、h1、t1等设计变量上增加一个正态分布的随机值进行突变设计，然后通过Simcode组件调用ABAQUS，执行Python参数化程序进行仿真计算，Calculator组件执行归一化处理，结果返回Optimization优化组件，选出本次优化的最优设计点，在此基础上进入下一次循环，由此形成回路，最终完成目标优化。

图9 倾角与支反力耦合多目标优化示意Fig.9 Schematic diagram of multi-objective optimization of inclination angle and reaction force

2.3 材料本构模型确定方法

气控驱动器由尼龙构成，对于这种塑料类的弹塑性材料，根据GB 1040—92《塑料拉伸性能试验方法》国家标准测试规范设计如图10所示哑铃状试样，进行单轴拉伸实验。其中，L0=40.00 mm为标称距离，b1=6.00 mm为试样宽度，h=2.00 mm为试样厚度。由拉伸实验获得L0区间的应力应变数据。

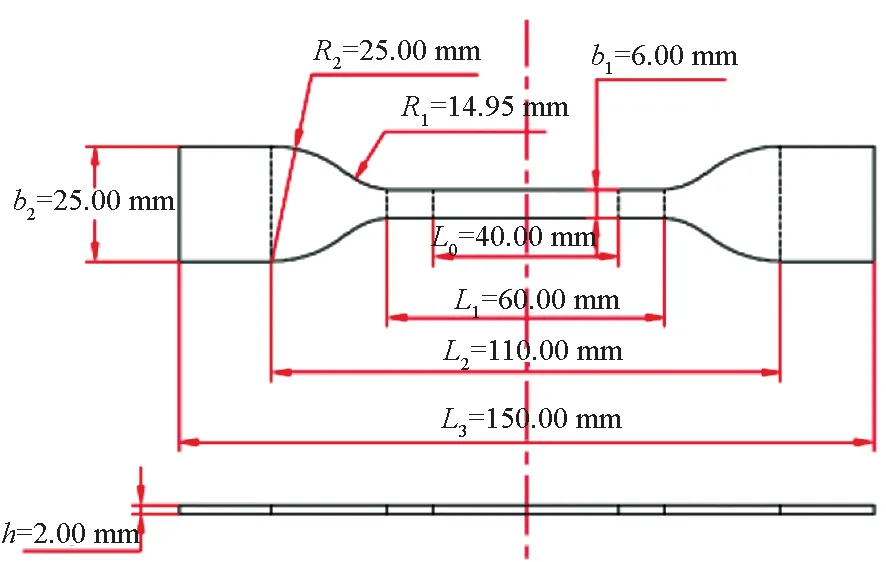
图10 尼龙材料单轴拉伸实验哑铃状试样Fig.10 Dumbbell shaped specimen for uniaxial tensile test of nylon

在处理名义应力应变数据之前，首先做如下假设：①物体内部无间隙，可以用连续性介质力学描述变形行为；②物体内部各个位置的物质具有相同特性，满足均匀性假设；③物体内部各个位置的材料属性为各向同性；④材料本构关系在线性阶段满足胡克定律，在塑性阶段满足各向同性硬化模型，即在强化阶段，屈服面的中心位置保持不变，形状只做相似的扩大；⑤在大变形行为中，应变为格林应变，应力为柯西应力；⑥在拉伸实验中，标称距离范围内各点的变形情况完全一致。

材料实验的数据常以名义应力应变的形式给出。在这种情况下，必须将名义数据转换为真实应力应变的值。真实应变与名义应变关系有

ε=ln(1+εnom)

(1)

式中，ε为真实应变或对数应变，εnom为名义应变。

考虑塑性变形的不可压缩性，并假定弹性变形也是不可压缩的，可以建立实际应力与名义应力之间的关系

σ=σnom(1+εnom)

(2)

式中，σ为实际应力，σnom为名义应力。

如图11所示为名义应力应变曲线和实际应力应变曲线。其中，屈服强度按0.2%残余应变计算，得σ0.2=15.18 MPa，σnom0.2=14.90 MPa；杨氏模量E=809.6 MPa，泊松比ν=0.35。

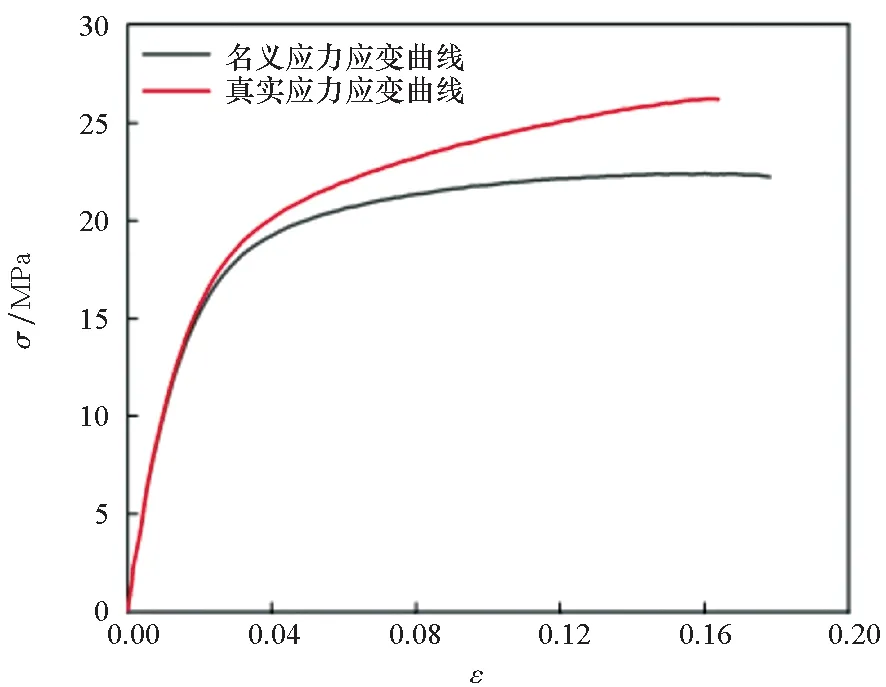
图11 名义与实际应力应变曲线Fig.11 Nominal and actual stress-strain curves

在结构有限元原理中，为方便计算屈服函数与硬化参数，需明确给出应力与塑性应变的数据。不同应变之间的关系有

(3)

式中，εp为塑性应变，εe为弹性应变。得到的实际塑性应力应变曲线如图12所示，最大等效塑性应变peeqmax=0.131 537。

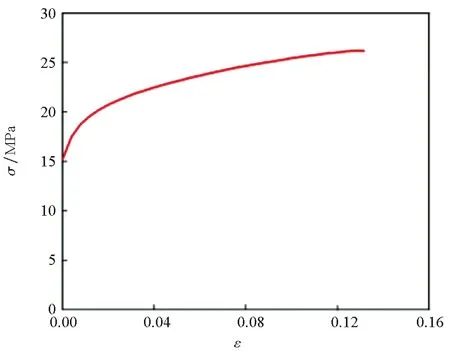
图12 实际塑性应力应变曲线Fig.12 Actual plastic stress-strain curve

3 结构参数敏感性分析

为分析不同尺寸参数变化对气控驱动器力学性能的影响程度，需要进行尺寸参数灵敏度分析。气控驱动器的变形优化包含两个载荷工况，为较清晰地获得因素对目标量的响应，采用单参数敏感性分析法分析尺寸参数对气控驱动器的力学性能的影响，单参数敏感性分析过程如下。

3.1 参数初值与设计范围

设计变量范围、初值以及响应量初值列于表1中。

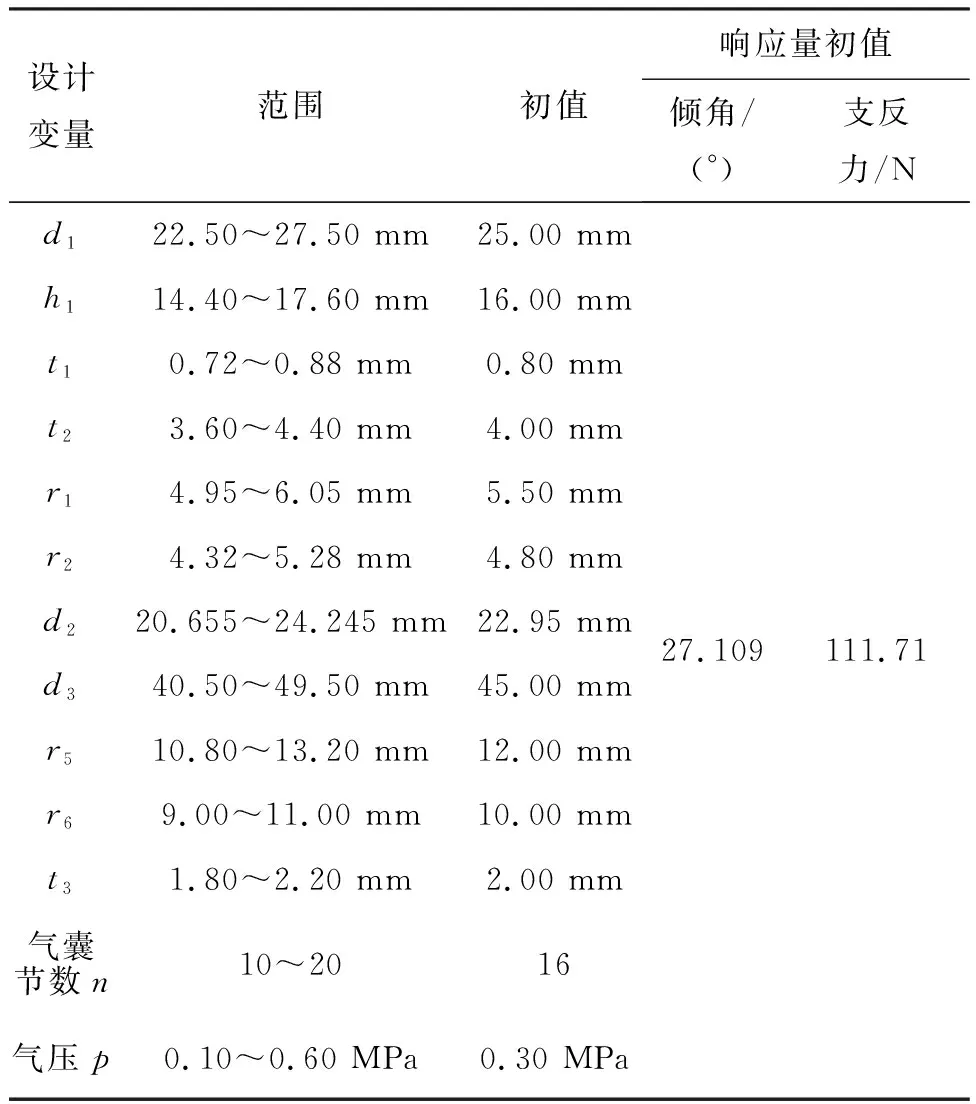
表1 设计变量与响应值初值

按物理含义，因子变量分为三类，分别为结构尺寸、气囊节数、气压。其中结构尺寸设计范围为±10%，若过小，则无法反映因子的影响；若过大，则可能出现几何结构的干涉错误。气囊节数与气压是独立于几何尺寸的，为了反映因子影响的广度，可以适当扩大设计范围，结果分别为10～20和0.10～0.60 MPa。

根据上述方式给出的设计变量范围和初值，可以得到单因子分析时的设计点，每个因子的水平数约为11。与初始值相比，采用控制变量法使每个设计点只有一个因子与其不同。在设计点因子分析过程中，各因子理论上在设定范围内线性均匀分布，但因子分析的实质是在不同参数组合下进行的有限元仿真分析，涉及收敛性等问题。部分因子在线性变化过程中的某个点可能会导致计算不收敛的问题，此时该因子的设计点取值在线性变化的基础上有轻微波动，各因子变化的总体趋势是在设定范围内均匀地线性分布。

3.2 单因子影响分析——倾角

该载荷工况下，气控驱动器底部固定，对一个气囊充压，结构发生弯曲变形，将弯曲倾角作为响应量。单因子影响结果表明，部分因子对响应结果几乎没有影响，还有部分因子对响应结果影响较小且无规律可循，剩下部分因子对响应结果影响较大且呈单调性，下面进行详细阐述。

如图13所示，这些因子的改变几乎不会引起倾角的变化。因为d2、r5、r6、t3因子均与薄板结构相关，进行单因子分析时，一个因子的变化无法显著改变形变方向上的刚度，并且外力方向和作用面积也与它们无关。

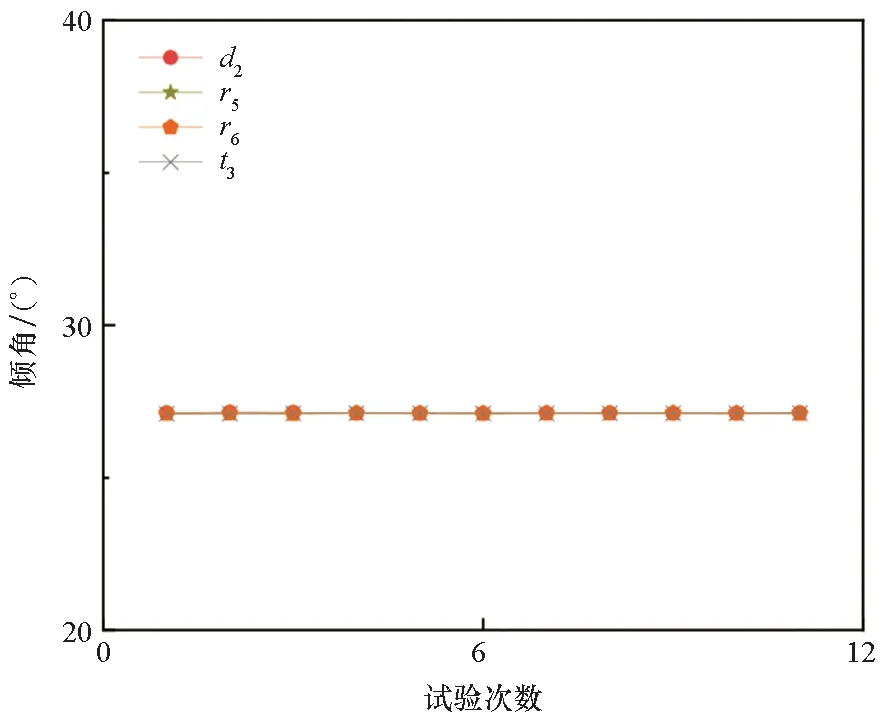
图13 倾角的低灵敏度影响因子Fig.13 Low sensitivity influence factor of inclination angle

如图14所示，这些因子为倾角的低敏感性参数，对倾角的影响也无规律可循。因为d1、h1、r1、r2、t1、t2因子均与波纹管气囊结构有关，进行单因子分析时，其中一个因子的变化在影响变形方向上结构刚度的同时，又改变了外力的作用面积或方向，进而直接导致刚度-位移-力平衡方程的改变，并且刚度和外力的变化方向可能不一致，这就出现了图中参差不齐的位移响应结果。

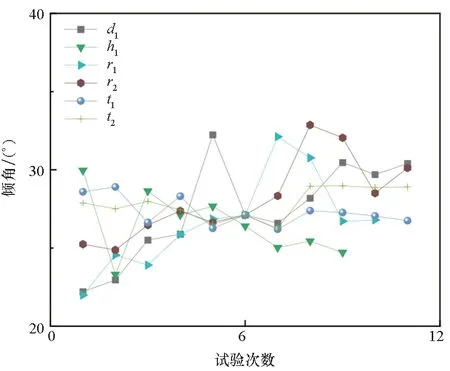
图14 倾角的低灵敏度且无规律分布的影响因子Fig.14 Low sensitivity and irregularly distributed influencing factors of inclination angle

如图15所示，倾角对气囊间距d3、气囊节数n和气压p的影响非常敏感且具有单调性。

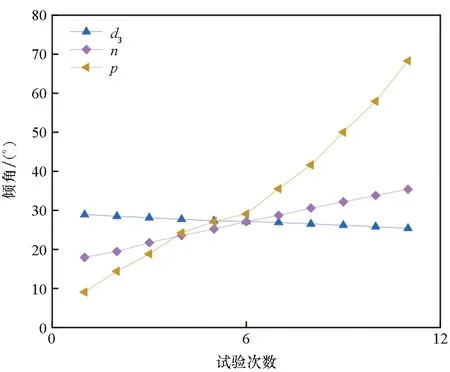
图15 倾角的高灵敏度影响因子Fig.15 High sensitivity influence factor of inclination angle

1)d3实际上为三个气囊的分布距离，随着气囊间距的增大，驱动器倾角逐渐减小。即当设计的结构较紧凑时，刚度反映的是整体结构抵抗变形的能力，在这种外力作用和变形模式下，变形方向上的刚度较大；而当设计的结构较分散时，刚度更多地反映局部结构抵抗变形的能力，在这种外力作用和变形模式下，变形方向上的刚度较小。

2)n代表气囊节数，结果表明，随着气囊节数增多，驱动器倾角也逐渐增大。如果将驱动器视为悬臂梁，当节数增加即悬臂梁的长度增加时，外力作用面积显著增大，继而使得力与弯矩同时增大。而由于结构尺寸未发生变化，所以惯性矩、抗弯截面系数及刚度均无改变，悬臂梁自由端挠度和转角增大。

3)气压p本质上是一种工艺参数，相比其余因子，它对响应结果影响程度最大。结果表明，随着气压值增大，倾角显著增大。因为其直接决定了外力的大小，从而对响应结果的影响也最直接。

3.3 单因子影响分析——支反力

该载荷工况下，气控驱动器两端同时固定，对一个气囊进行充压，主要实现内部挤压，将顶部支反力作为响应量。由于施加压力载荷，每个位置载荷均垂直作用面，顶部支反力反映的是顶部气囊的受力，尽管整体受力平衡，但不从整体角度作受力分析。两端均受约束的气囊，可以简化为杆件，内部或局部受力，产生挤压。下面通过分析因子对外力与刚度的影响(本质上与刚度无关，只为方便分析)，来间接描述对顶部支反力的作用。

如图16与图17所示，这些因子对支反力的影响较小：①与气囊相关的t1、t2、r1、r2因子，进行单因子分析时，虽然这些因子的变化引起气压局部作用面积的变化，但对横向截面面积影响较小。即对受面积和形状影响的截面刚度影响较小，甚至外力与刚度的变化处于一种互相抵消的状态。如图所示，支反力作为一种约束边界上的合外力，正好反映出这种影响本质。②d2、d3、r5、r6、t3因子与薄板有关，参照倾角分析部分，进行单因子分析时，它们对受力位置处的刚度与面积影响有限，故对支反力影响较小。③如果把气囊节数n比作杆件的长度，当外力不变时，它的变化不会引起应力和应变的改变，也不会影响力平衡状态。

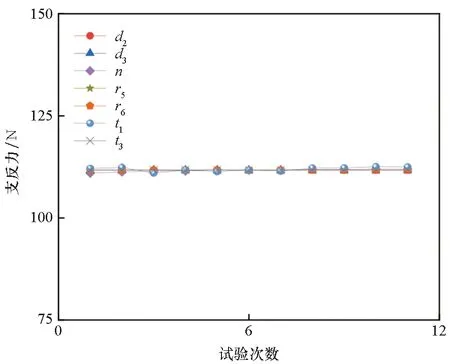
图16 支反力的低灵敏度影响因子(薄板)Fig.16 Low sensitivity influence factor of reaction force (thin plate)

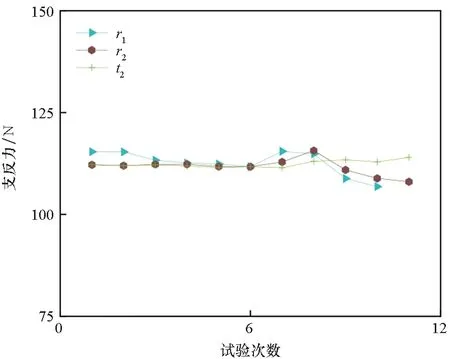
图17 支反力的低灵敏度影响因子(气囊)Fig.17 Low sensitivity influence factor of reaction force (airbag)

如图18所示，这些因子对支反力的影响较大且呈单调性：①d1与h1分别决定了气囊在横向和纵向上的尺寸。结果表明，随着d1增大，支反力也逐渐增大：因为d1越大，气压作用面积越大，则合力越大。随着h1增大，支反力逐渐减小：因为h1增大，间接影响了其他结构的位置关系，导致横向整体面积减小(纵向面积不会影响)，所以合外力减小。②同理，气压p本质上是一种工艺参数，相比其余因子，它的影响程度最明显。结果表明，随着气压值增大，支反力显著增大。

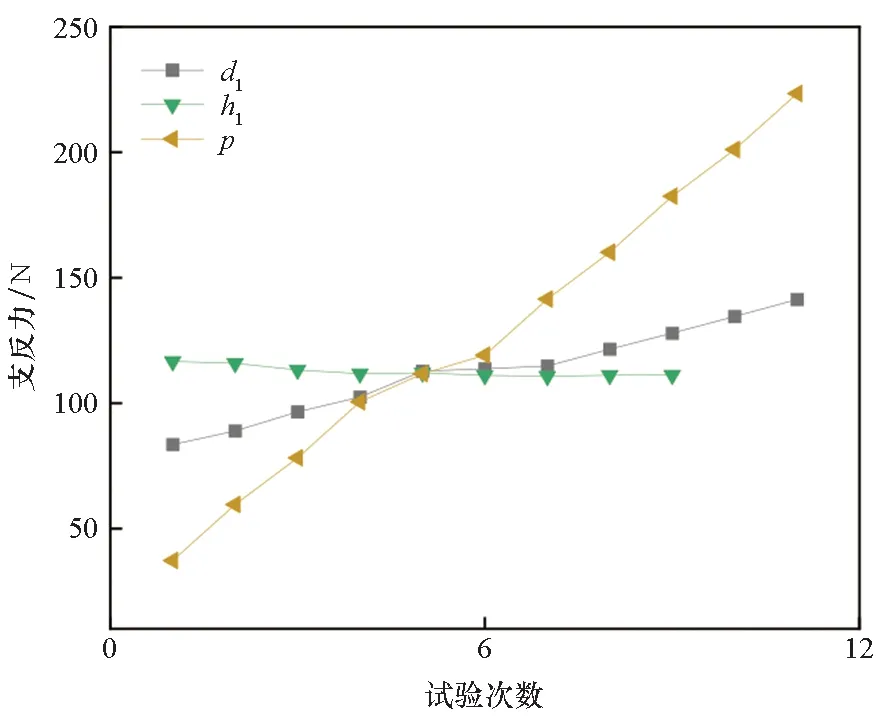
图18 支反力的高灵敏度影响因子Fig.18 High sensitivity influence factor of reaction force

3.4 分析结论

1)气囊节数n和气压p与响应值间呈较为明显的单调性规律，影响较大，但气囊节数和气压实质上不同于尺寸因子，两者与尺寸因子相互独立，所以不将两者作为优化变量考虑，仅选择结构尺寸因子作为优化变量。

2)以结构尺寸因子的倾角或支反力响应初值为分母，将该因子在设计变量区间内倾角或支反力的变化差值作为分子，计算得到相应因子灵敏度。结构尺寸因子对倾角与支反力的灵敏度如表2所示。可以看到，d1、h1、r1、r2对倾角的影响均超过10%，其他因子影响较小；d1对支反力的影响最大且呈单调递增趋势，数值接近25.4%，其余因子影响则均较小。

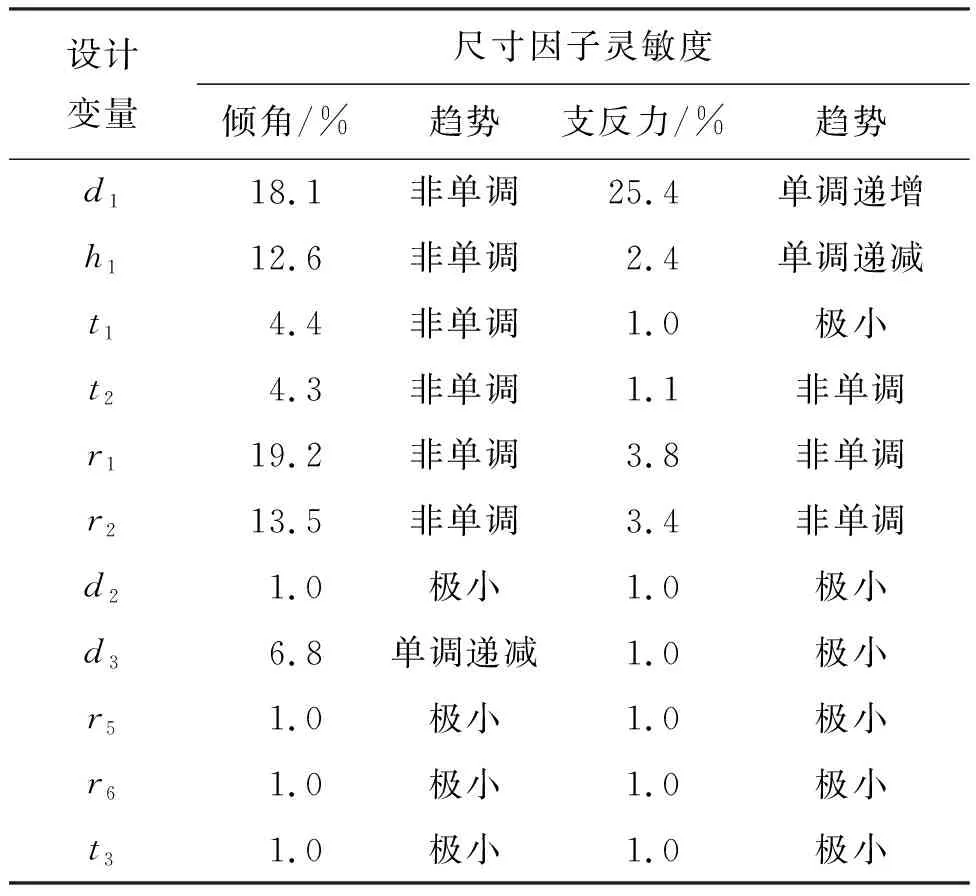
表2 结构尺寸因子灵敏度

4 结构优化与性能评估

基于第3节选取较为敏感的结构尺寸参数，对其进行优化。根据3.4节的结论，气囊节数n和气压p不作为优化参数。在后续优化过程中气囊节数n和气压p按照表1中的初始值进行设置，分别为16节和0.3 MPa。优化步骤如下：

1)载荷工况一优化：以倾角作为单一优化目标获得其最大值；

2)载荷工况二优化：以支反力作为单一优化目标获得其最大值；

3)多目标耦合优化：根据步骤1和步骤2优化结果，对倾角与支反力作归一化处理，进行加权作多目标耦合优化。

除了确定优化变量与优化目标量之外，还需给定约束条件。为保证结构的合理性，应设定尺寸约束；为判断收敛性，应设定布尔值；为避免结构破坏，应给定变形极限，这里为最大等效塑性应变peeqmax=0.131 537。

4.1 全局目标函数建立

由倾角和支反力单一优化目标优化结果可得两个优化目标的最大值分别为Amax、Fmax，然后将其作为分母，进行优化目标归一化处理，有

(4)

其中，ACoefficient表示倾角归一化系数，FCoefficient表示支反力归一化系数，暂取fA∶fF= 1 ∶1。

4.2 单目标最大值计算

4.2.1 倾角优化

设置的优化次数为100，但因结构错误与收敛性等原因，计算成功的次数约为50。如图19(a)所示为倾角优化数值统计结果，其中，红点表示失败点，黑点为非最优点，绿点为最优点。图19(b)表示仿真模型的全局最大等效塑性应变，可以看到，部分设计点计算的等效塑性应变超过最大塑性应变，最终判定为失败点。

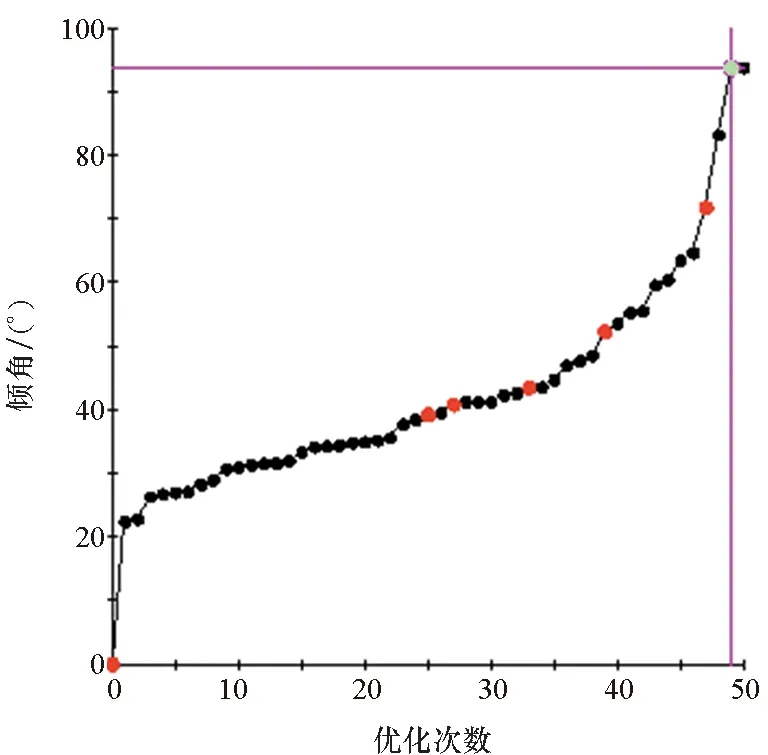
(a) 倾角数值(a) Inclination angle value

表3为设计变量与优化结果，可以看到最终Amax=93.787°，约是初值27.109°的3.5倍。

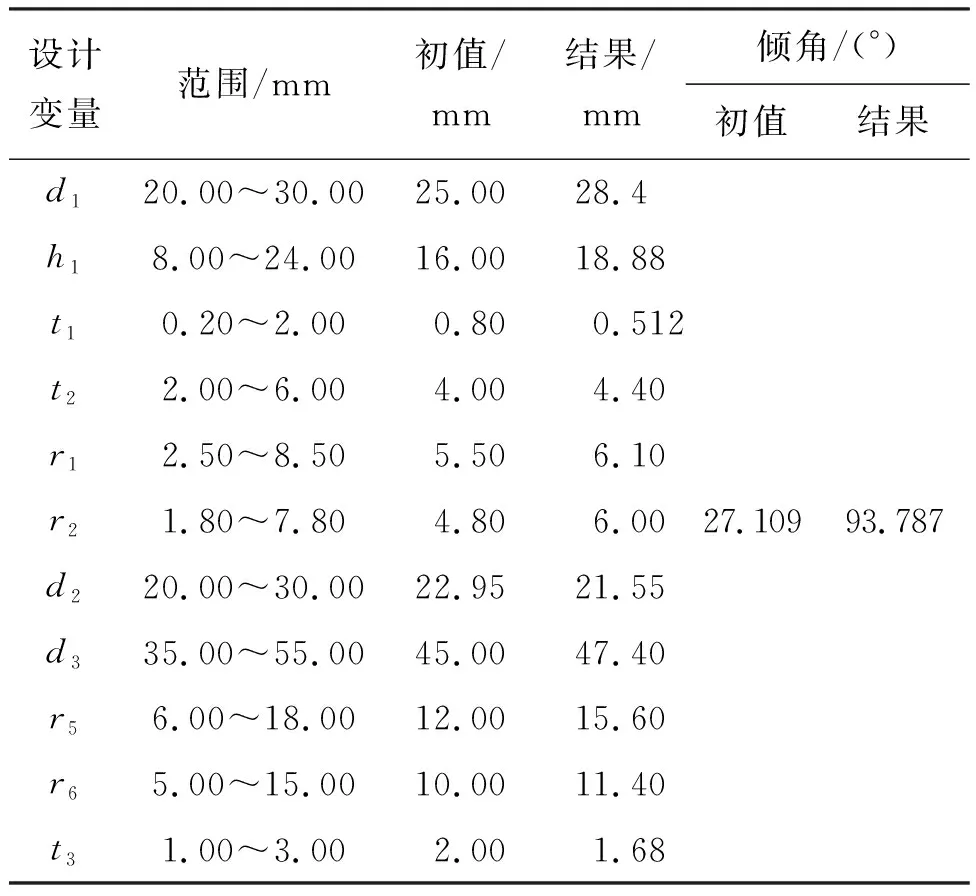
表3 倾角设计变量与优化结果

4.2.2 支反力优化

如图20(a)所示为支反力优化数值统计结果，其中，红点表示失败点，黑点为非最优点，绿点为最优点。图20(b)表示仿真模型的全局最大等效塑性应变。

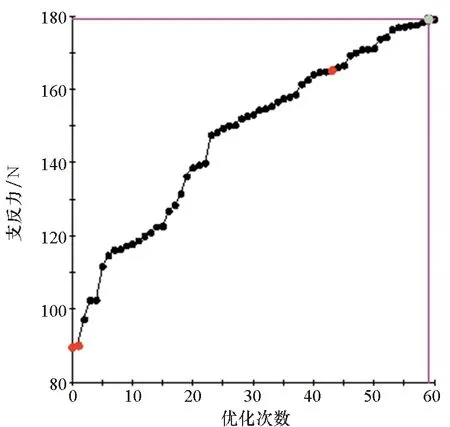
(a) 支反力数值(a) Reaction force value

表4为设计变量与优化结果，可以看到最终的Fmax=179.2 N，约是初值111.71 N的1.6倍。

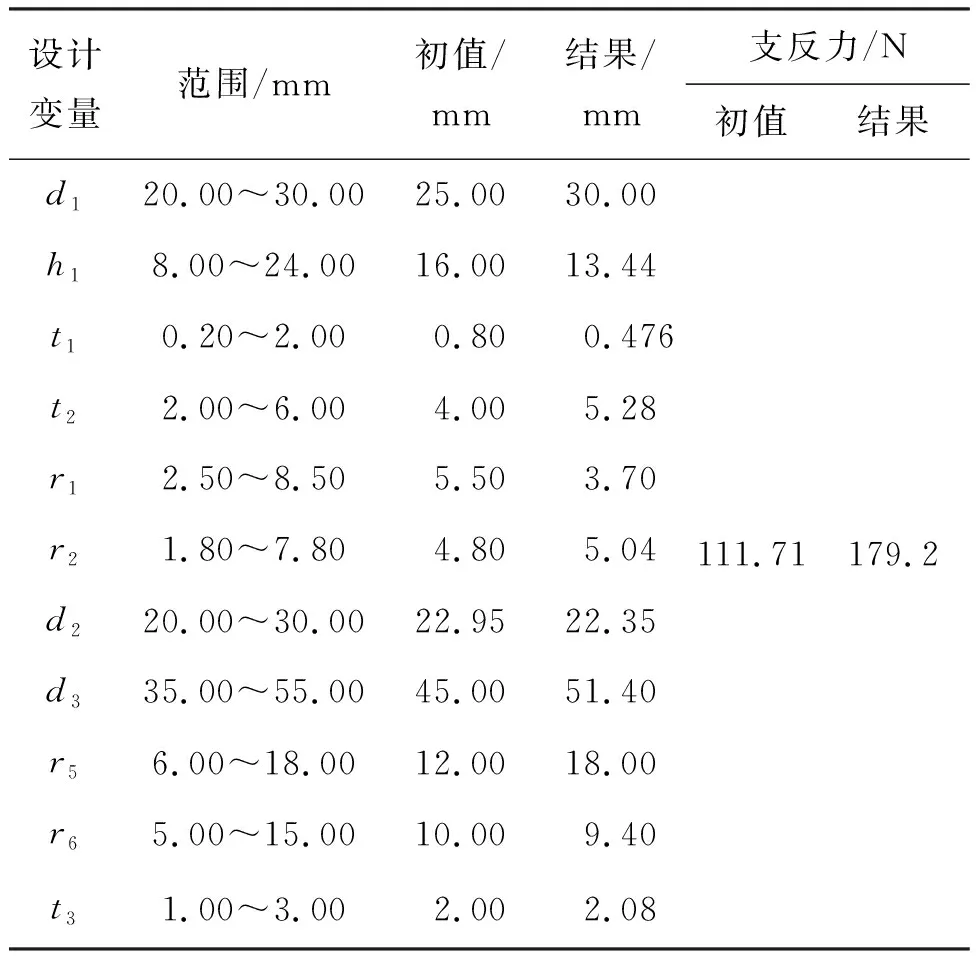
表4 支反力设计变量与优化结果

4.3 全局优化实施

由上述单目标计算可得最大值分别为Amax=93.787°、Fmax=179.2 N，将优化次数设置为100。

如图21(a)所示为ACoefficient统计结果，其中，红点表示失败点，黑点为非最优点，蓝点为某一优化变量在此时取得最大值，绿点为最优点。如图21(b)所示为FCoefficient统计结果。

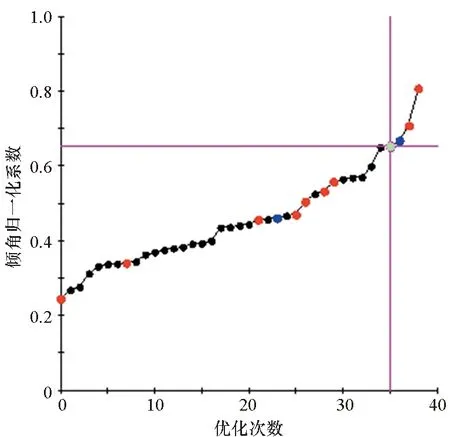
(a) ACoefficient

在耦合优化目标取得最优解时，倾角归一化系数ACoefficient=0.652 52，支反力归一化系数FCoefficient=0.788 75，据此可计算出A=64.054°，F=144.105 N。此时的优化变量值与优化目标值均列于表5中。从表5结果可以看出，全局目标优化后的支反力与倾角相比初值分别提升了29%、136%，得到了气控驱动器最优参数组合。

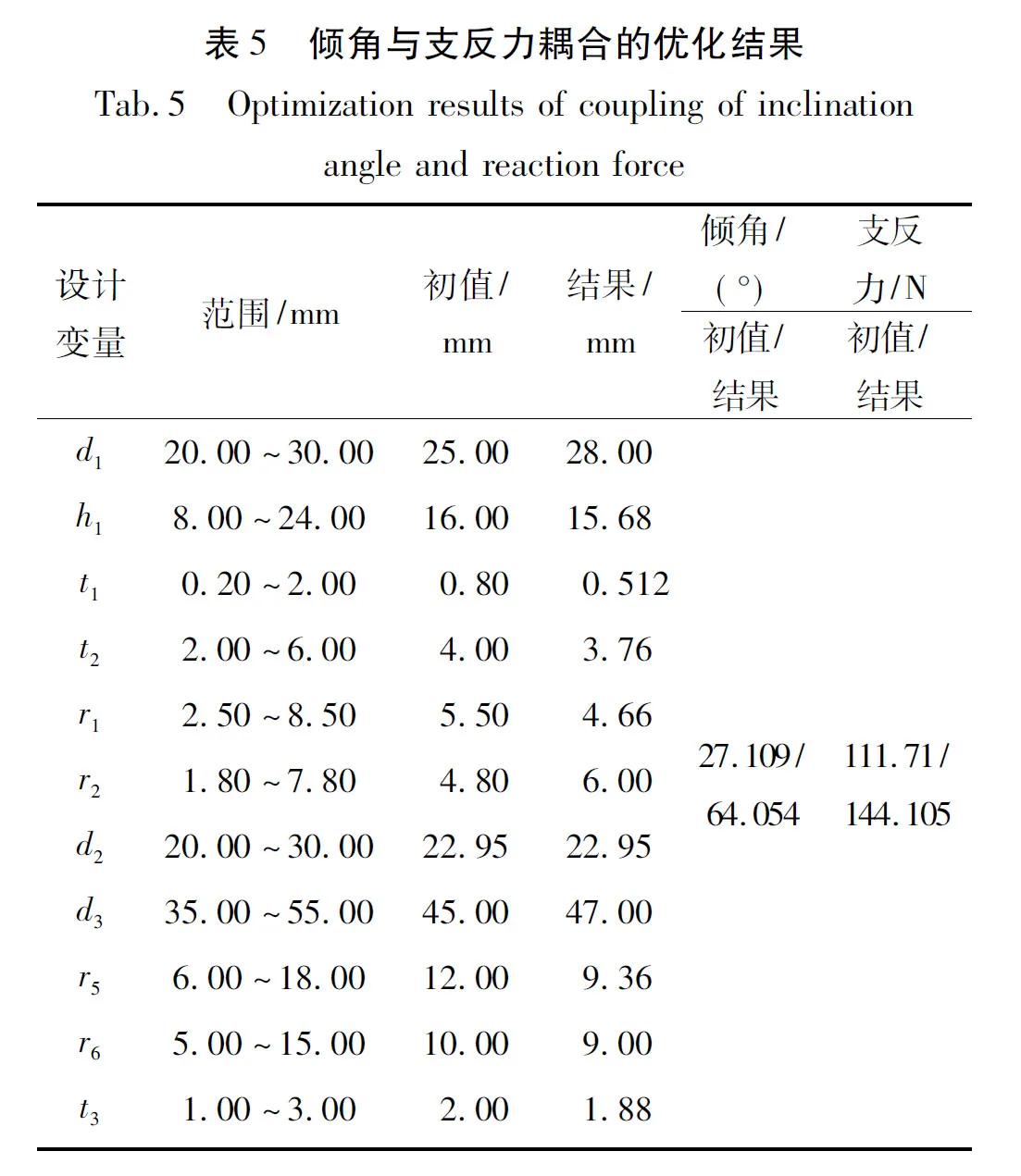
4.4 气控驱动器优化结果

用两种载荷工况对优化后的气控驱动器进行仿真分析，模拟结果如图22所示。可以看到，工况一条件下，在内部气压作用下，驱动器弯曲并发生塑性变形。前已述之，等效塑性应变应小于最大等效塑性应变peeqmax=0.131 537；此外，由于塑性变形无法恢复，在气压撤销之后，存在残余应变。据此建议，在所加气压作用下(本仿真中气压为0.3 MPa)，驱动器应最好不发生塑性变形。工况二条件下，结构在气压作用下，产生的Mises应力与等效塑性应变相比工况一均较小，且几乎未发生塑性应变，处于安全形变范围之内。

(a) 工况一下Mises等效应力与等效塑性应变(a) Mises equivalent stress and equivalent plastic strainunder working condition 1

5 结论

针对气控软体驱动器设计优化问题，以弯曲倾角和支反力为评价目标，提出气控软体驱动器的结构分析与优化设计方法。主要工作及结论如下：

1)自主开发几何参数化程序，将仿真计算的非线性算法与Evol优化算法耦合，高效、稳定地实现特征参数优化，并进一步确立了软体驱动器各个几何特征之间的两大类型约束关系，最后对各参数进行灵敏度分析，确定高敏感度参数。

2)运用归一化与加权策略及Evol优化算法对倾角与支反力进行全局目标优化，成功将支反力和倾角分别提升了29%、136%，得到了最优参数组合。

3)由于气囊节数和气压本质为工艺参数，并独立于结构尺寸因子，本文没有将两者作为优化变量进行分析。根据现有结论无法推断两者变化对“支反力和倾角分别提升29%、136%”优化结果的影响。在后续研究中，会考虑将主成分分析或降维方法引入多变量优化方法，将气囊节数、气压和结构尺寸因子同时作为优化变量，开展对驱动器的优化设计。

4)由于气控驱动器优化参数较多，当几何拓扑发生变化或者结构变动较大时，可能出现干涉等几何错误。为了获得适用范围更广的优化设计，未来可以采用拓扑优化的方式进行软体驱动器设计。

5)在敏感性分析方法上，若直接采用正交试验、中心因子组合试验、超拉丁方试验等多因子分析方法，不仅计算量过大，而且结果也很难收敛在一个合理的范围内。未来可采用遗传算法或人工神经网络对现有特征参数进行进一步分析，结合拓扑优化的结果，将软体驱动器的倾角和支反力推向新的极限。