超音速气流中热塑性复合材料壁板的非线性热颤振特性*
2022-04-06高艺航段静波雷勇军
高艺航,段静波,雷勇军
(1. 国防科技大学 空天科学学院, 湖南 长沙 410073; 2. 中国运载火箭技术研究院 北京宇航系统工程研究所, 北京 100076;3. 石家庄铁道大学 工程力学系, 河北 石家庄 050043)
随着航天器朝着高速、强突防、低成本、短周期方向发展,对结构构件的材料与成型提出了更高的要求。热塑性树脂基复合材料由于其耐高温、高强度、高韧性、可重复使用等诸多优异性能,成为可重复使用航天器首选的先进复合材料。然而,热塑性复合材料基体韧性大,受热塑性显著,在航天器极端复杂的气动热环境中,热塑性复合材料制成的壁板类结构的气动弹性力学行力及机理十分值得研究。
关于壁板热颤振问题的研究最早可以追溯到 20 世纪50年代,Houbolt[1]最先开始研究温度场均匀分布的二维壁板颤振边界及其屈曲失稳特性。随后,Dowell[2]针对金属壁板几何非线性颤振问题进行了大量研究。Kouchakzadeh等[3]采用经典板理论和von Karman非线性位移应变关系进行结构建模,研究复合材料层合板在超音速气流中的非线性气动弹性问题。如果飞行马赫数较高,在强烈的气动加热效应作用下,壁板将面临极端严酷的热环境。Zhou等[4]发现受热壁板在气流中的运动形式极其复杂,具有从低速气流中的衰减振动、热屈曲振动形式到高速气流中各种类型的振动。杨智春等[5]采用分步分析方法研究了复合材料铺层方式对壁板热颤振特性的影响。李凯伦等[6]对高超声速环境中功能梯度薄板的热气动弹性问题进行了研究,发现气动加热效应能够使薄板发生热屈曲或者提前进入振动状态。Yang等[7-8]针对高超声速飞行器一体化防热结构,建立了泡沫填充复合材料波纹夹芯板的高阶分层气动弹性模型,讨论了几何参数和材料性能对颤振临界动压的影响。Li等[9]研究了三角形栅格芯夹层板在超音速气流中的颤振和屈曲,并采用位移反馈的方法设计了主动控制器,为夹层结构在飞行器设计中的应用提供了理论依据。
关于热塑性复合材料,Özen等[10]分别采用实验和仿真分析方法研究了热塑性蜂窝夹芯板低能量冲击响应特性。Chen等[11]设计和制备了多层热塑性复合材料(ThermoPlastic Composite, TPC)波纹夹芯板,采用平板压缩试验研究了芯材结构的失效机理。目前,公开的文献资料大多是关于热塑性复合材料的制造工艺、本构关系、弹塑性变形、损伤测试方面的研究[12],而关于热塑性复合材料壁板的颤振问题报道还比较少[13-15]。基于此,本文以热塑性复合材料层合板为研究对象,研究其颤振特性,分析关键参数对壁板热颤振特性的影响规律。
1 超音速流场中复合壁板颤振有限元方程
1.1 结构模型
如图1所示,矩型热塑性复合材料壁板的长度和宽度分别为L和H,厚度为h。由于复合材料壁板属于厚板,因而,本文采用Mindlin厚板理论,壁板内任意一点的位移场可写为:
(1)
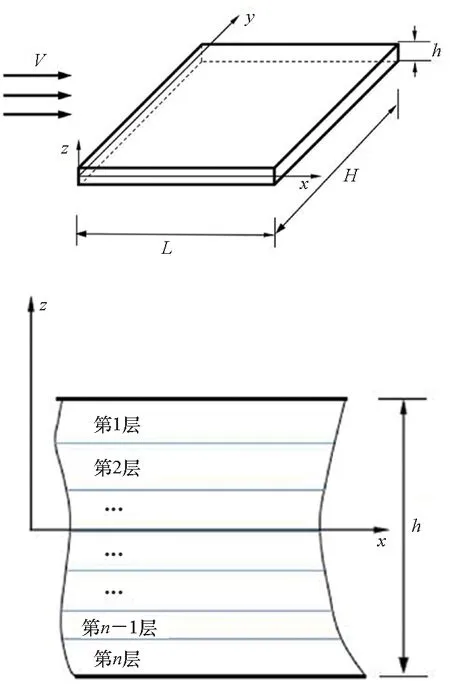
图1 热塑性复合材料壁板示意图Fig.1 Sketch of thermoplastic composite panel
其中,u0、υ0、w0分别为中面上的点沿x轴、y轴和z轴方向的位移,θx和θy分别为中面法向转角。
考虑高速气流作用下壁板可能产生的几何非线性变形,采用Von-Karman大变形理论,给出热塑性壁板的应变-位移关系如下:
(2)
其中:ε0包括壁板中面面内位移产生的应变分量和壁板大变形时挠度引起的非线性应变分量;κ为弯曲时壁板的曲率向量;γ为横向剪切应变向量;z为壁板厚度方向的坐标。
在热塑性壁板应力-应变关系方面,考虑温度对热塑性壁板热应力的影响以及材料力学性能随温度的变化,暂不引入应力应变的塑性本构关系,但在分析中讨论屈服极限对壁板颤振应力的影响。对于第k铺层,并忽略法向正应力,则壁板应力-应变关系为:
(3)
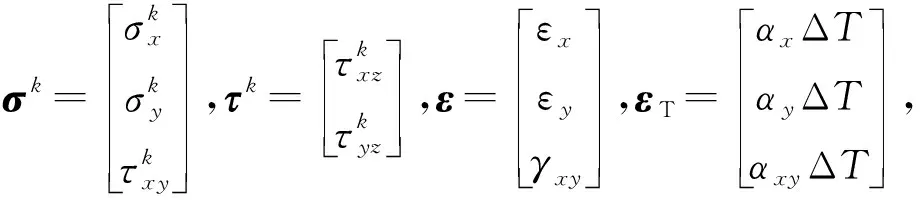
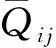
根据复合材料层合理论,n层复合变刚度壁板本构关系可写为:
(4)
其中,N、M、Fs分别为复合变刚度壁板的膜力、弯矩、横向剪力等内力,矩阵A、B、D、As见文献[16],矩阵NT、MT的表达式为:
(5)
1.2 气动力模型
在Ma>1.6的高速气流中,壁板颤振可采用一阶准定常活塞理论计算气动力。 当壁板表面来流沿x方向时,气动力表达式[17]为:
(6)
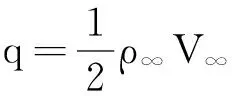
1.3 非线性颤振有限元方程
根据Hamilton原理,建立复合壁板的运动微分方程,即
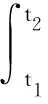
(7)
其中,δT和δU分别为虚动能和虚应变能,δW为气动力和结构阻尼所做的虚功。
基于复合壁板本构关系、几何关系以及气动力模型,分别写出壁板体积域V内的虚应变能和虚动能,以及其表面S上的外力虚功。 其中,虚应变能包括壁板振动产生的应变能δUM和热载荷产生的应变能δUΔT两部分,具体如下:
(8)
运用有限元方法求解壁板颤振,采用四边形四节点板单元对壁板进行网格离散,总体位移列阵可记为如下形式:
(9)
其中
(10)
将总体位移列阵代入式(8),通过变分则可获得壁板的有限元颤振方程:
(11)
(12)
1.4 复合材料屈服准则
基于Hill正交各向异性屈服准则,Chen和Sun提出了适用于各向异性纤维增强复合材料的三维塑性势函数。Weeks和Sun进一步假设复合材料在纤维方向1上是线弹性的,在纤维方向2~3 面内是横观各向同性的,从而将三维塑性势函数简化为[14]:
(13)
本文研究的热塑性C/PPS材料为缎纹机织复合材料,材料在纤维方向1、2上是线弹性的,且不考虑纤维方向3(厚度方向)的正应力σ33,因而,上述塑性势函数可最终退化为:
(14)
2 算例验证与分析
2.1 正确性验证
根据文献[18]中T300/5208型环氧树脂复合材料壁板算例,壁板几何尺寸为0.3 m×0.12 m,厚度为1 mm,具体材料参数取值及颤振动压无量纲化与文献[18]一致,采用本文程序进行了固有频率及颤振速度计算,结果见表1和表2。从表1中可以看出,本文计算的固有频率与文献结果吻合较好。采用有限元法分析时,通常需要通过细密网格才能保证分析结果的精度。因此,需要进行网格收敛性验证。
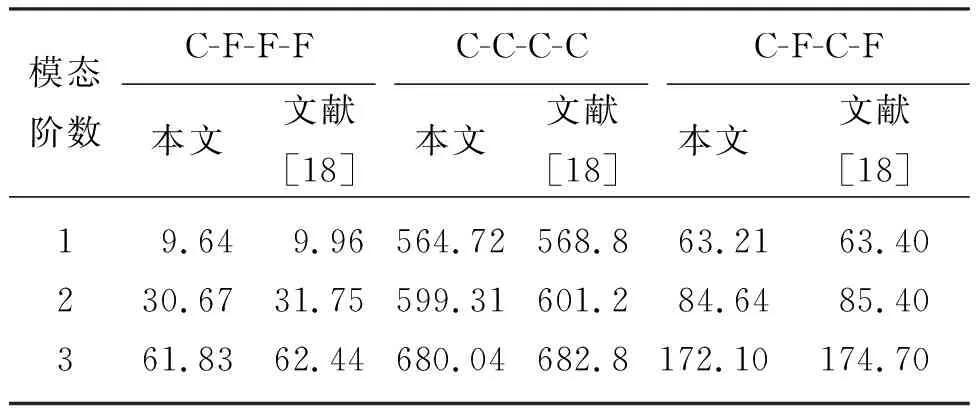
表1 环氧树脂复合材料壁板固有频率
从表2中可以看到,随着网格划分数量增多,结果逐渐收敛。当网格划分数为40×16时,本文颤振速度计算结果与文献吻合得很好。因此,综合考虑线性壁板颤振的计算精度和效率,本文后续计算均采用40×16的网格数量。
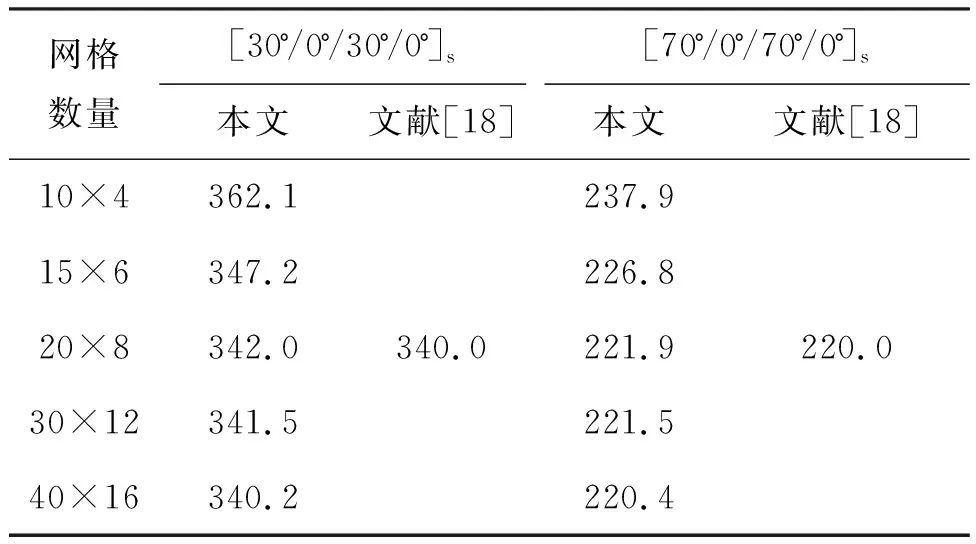
表2 环氧树脂复合材料壁板无量纲颤振动压
2.2 频域线性颤振分析
以四边简支的C/PPS热塑性复合材料矩形壁板为对象,采用有限元法求解研究其热固有特性和频域热颤振特性。热塑性复合材料密度为0.9~1.6 g/cm3,本文计算中取1.25 g/cm3,泊松比取0.08,热膨胀系数取1.6×10-6℃,其随温度变化的材料力学性能参数见表3[15]。壁板几何尺寸为0.4 m×0.2 m,厚度为3 mm,铺层方式为[0]7,来流方向平行于x轴。
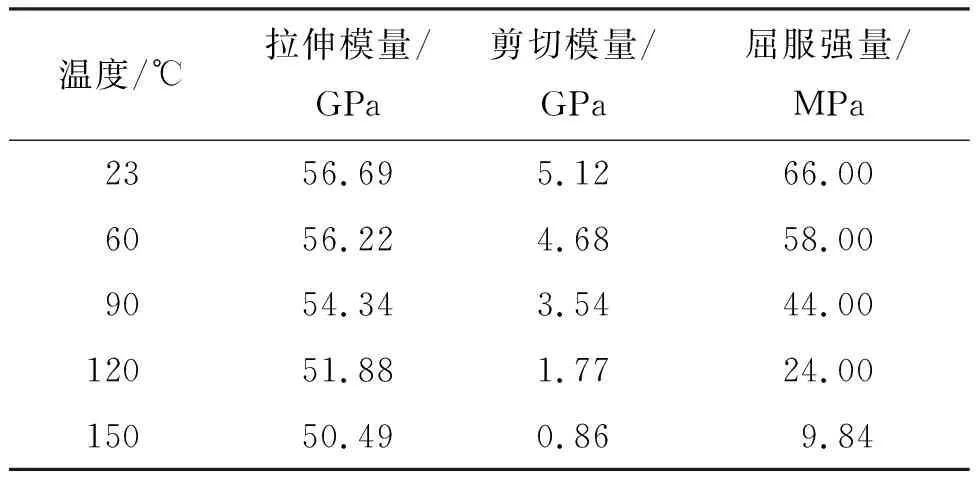
表3 热塑性材料力学性能参数
由于温度载荷不仅产生热应力,而且温度还改变材料的力学性能,这两方面均对壁板颤振产生影响。热塑性材料受温度变化影响较大,需要同时考虑两方面的影响。本文采用V-g法求解热塑性复合材料壁板频域颤振特性,并分析材料力学性能随温度变化对热塑性复合材料壁板热颤振特性的影响。
图2分别给出了60 ℃和90 ℃下壁板前两阶模态阻尼随无量纲动压的变化规律。壁板无量纲颤振动压定义见文献[19]。从图2中可以看到,两种温度下壁板热颤振均由1阶模态和2阶模态耦合引起。在60 ℃下,由阻尼曲线在来流动压为211.0时过零点,这说明壁板的无量纲颤振动压为211.0。同样,在90 ℃下,由阻尼曲线过零点可得知,壁板无量纲颤振动压为149.5。
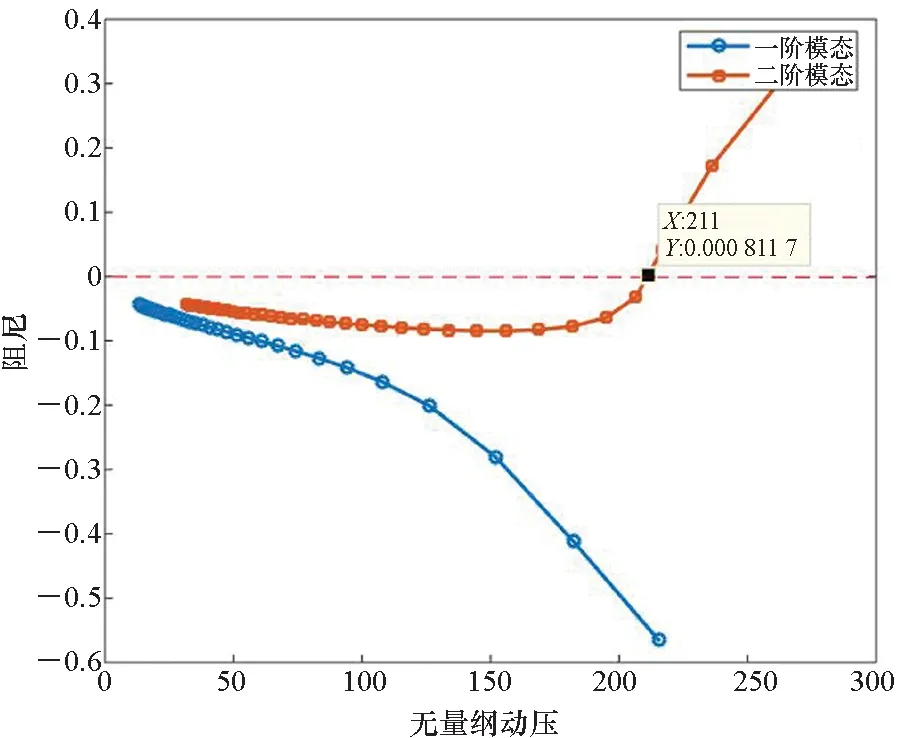
(a) 60 ℃下壁板的模态耦合(a) Modal coupling of the panel at 60 ℃
图3给出了23 ℃、60 ℃、90 ℃、120 ℃四个温度下考虑与不考虑材料性能随温度变化两种情况下热塑性壁板的热颤振特性。总体上看,温度的升高显著降低了壁板的颤振动压。在常温23 ℃下,壁板颤振无量纲动压最大。考虑热塑性材料温变后得到的壁板无量纲动压低于仅考虑热应力时的颤振动压,从图3中可以看到,在60 ℃、90 ℃、120 ℃下,壁板无量纲动压分别降低了5.1、17.0、34.8。由此可得出,考虑材料性能随温度变化后,得出的壁板颤振动压更低,而且温度越高,材料性能随温度变化对壁板颤振特性影响越明显。
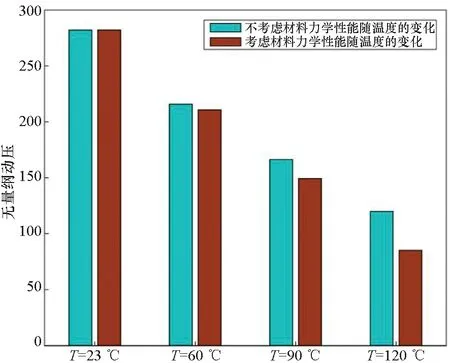
图3 不同温度下热塑性壁板热颤振动压Fig.3 Thermal flutter dynamic pressure of thermoplastic panels at different temperatures
2.3 时域非线性颤振分析
以四边简支的C/PPS热塑性复合材料壁板为对象,采用有限元法从时域求解壁板非线性热颤振特性。
图4~6给出了60 ℃时热塑性复合材料壁板特征点(0.5a,0.5b)在不同来流速度下的颤振时间历程和相平面图。从图4可以看到,当来流动压λ=188.6时,壁板受到初始扰动后,振动是收敛的,这表明动压未达到颤振临界动压。当来流动压λ=213.7时,壁板受到初始扰动后,进入极限环振动,振幅数量级为1.7×10-3mm,此时动压超过颤振临界动压,壁板做周期振动,发生颤振,如图5所示。当动压进一步增大,取来流动压λ=234.7时,壁板受到初始扰动后,仍处于颤振极限环振动,但是壁板做周期振动的振幅增大为4.3×10-1mm,如图6所示。
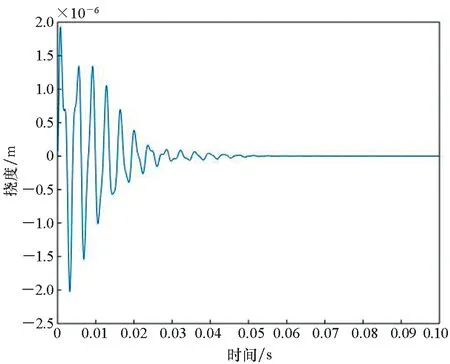
(a) 板中点位置挠度-时间曲线(a) Time history plot of deflection at the centre of the plate
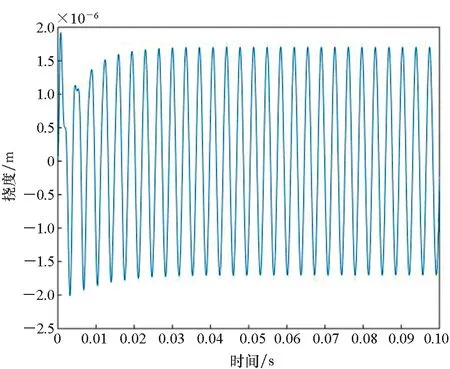
(a) 板中点位置挠度时间曲线(a) Time history plot of deflection at the centre of the plate
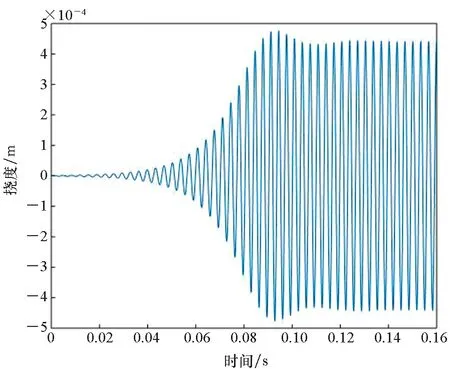
(a) 板中点位置挠度时间曲线(a) Time history plot of deflection at the centre of the plate
图7给出了热塑性复合材料壁板在23 ℃、60 ℃、90 ℃、120 ℃下壁板极限环振幅随无量纲动压的变化情况。从图7中可以看出,不同温度下壁板的颤振极限环振幅随动压的增大而增大,增大趋势基本一致。但随着温度从23 ℃逐渐增加到120 ℃,壁板进入颤振的动压越来越低。此外,从图7中还可以看出考虑与不考虑材料性能随温度变化对壁板极限环振幅的影响。在常温23 ℃下,两者没有差异。在60 ℃下,考虑材料力学性能随温度变化时,壁板进入颤振的动压低于不考虑材料力学性能随温度变化的情况。与此同时,相同动压下,考虑材料力学性能随温度变化时的极限环振幅要高于不考虑材料力学性能随温度变化的情况。在90 ℃、120 ℃下,规律相似于60 ℃的情形,只是壁板进入颤振的动压差值随着温度从60 ℃到120 ℃逐渐增大,相同动压下,极限环振幅差异也越来越大。
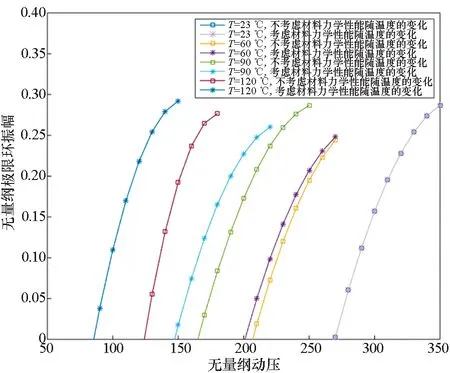
图7 不同温度下壁板极限环振幅随无量纲动压的变化Fig.7 Change of limit cycle amplitude of the panel along with dimensionless dynamic pressure at different temperatures
2.4 颤振应力分析
文献[15]给出的不同温度下剪切试验数据表明,C/PPS热塑性材料剪切强度都随着温度的增加而出现明显的降低,在120 ℃时剪切强度比常温时降低了63.64%。对于热塑性壁板,在颤振发生过程中,如果应力响应达到材料塑性屈服强度将引起不可恢复的永久变形,这是热塑性壁板热颤振设计中需要考虑的问题。下面仍以四边简支的C/PPS热塑性复合壁板为例,研究壁板颤振亚临界过程中的应力变化情况。
图8给出了热塑性复合材料壁板分别在23 ℃、60 ℃、90 ℃、120 ℃下,壁板极限环振荡下等效应力幅值随动压变化的情况。从图8中可以看到,在同一温度下,随着动压增大,壁板的应力水平在增大。例如在23 ℃时,随着壁板颤振动压由280.5增加到322.1,颤振等效应力由0.399 MPa增加到1.27 MPa;在60 ℃时,随着壁板颤振动压由220.2增加到216.7,颤振等效应力由0.462 MPa增加到0.840 MPa。比较不同温度下壁板的颤振等效应力,可以看出,随着壁板温度的升高,在温度应力和材料温变的共同作用下,壁板颤振等效应力是逐渐降低。原因在于,温度产生的结构温度应力是压应力,而壁板颤振产生的应力是反向的拉应力,两者呈现相互抵消的效应,且温度越高,抵消效应越明显。此外,从图8中可以发现,壁板极限环振荡下等效应力幅值总体较小,均没有达到各温度下C/PPS热塑性复合材料的屈服极限(见表3),壁板没有出现屈服区域。这主要是由于壁板颤振过程中产生的主要是双向拉或压应力状态,切应力较小,而等效应力则是反映切应力水平,因而壁板极限环振荡下等效应力幅值总体较小。
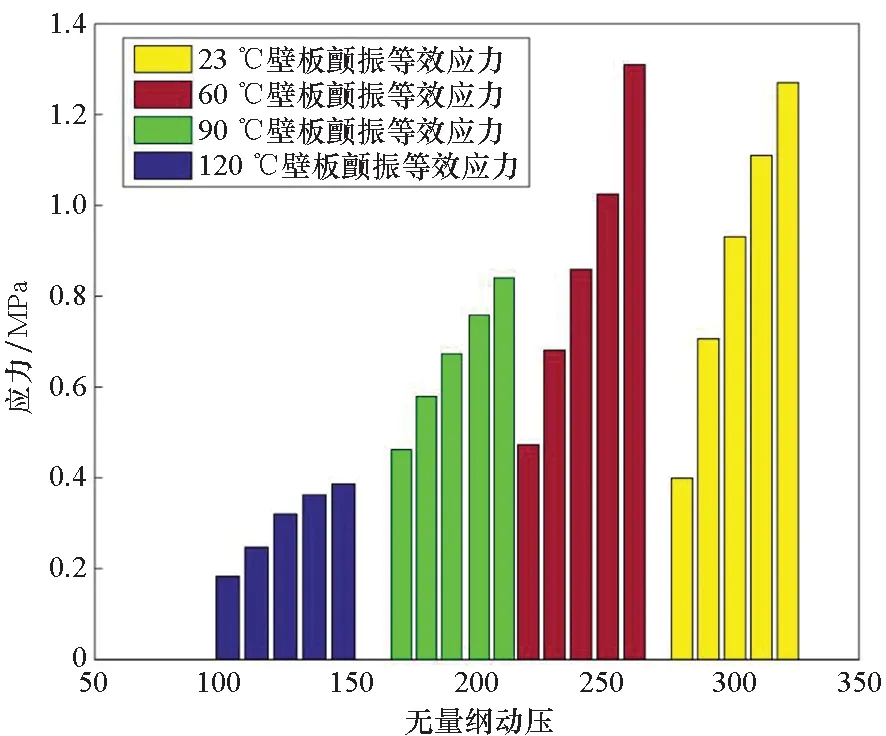
图8 不同温度下壁板极限环振荡等效应力变化Fig.8 Change of limit cycle oscillation equivalent stress of the panel at different temperatures
3 结论
本文建立了超音速流场中热塑性复合材料壁板热颤振的有限元模型,与相应文献结果进行对比,验证了本文模型及算法的正确性。进而采用V-g法、Newmark法分别从频域、时域求解复合变刚度壁板颤振特性,得出的主要结论如下:
1)热塑性壁板热颤振由1阶模态(纵向一弯)和2阶模态(纵向二弯)耦合产生,随着温度的升高,壁板的颤振动压显著降低,而且考虑热塑性材料温变特性后得到的壁板颤振动压要低于仅考虑热应力时的颤振动压。
2)不同温度下,当考虑材料力学性能随温度变化时,壁板进入颤振的动压低于不考虑材料力学性能随温度变化的情况。与此同时,相同来流动压下,考虑材料力学性能随温度变化时的极限环振幅要高于不考虑材料力学性能随温度变化的情况。
3)随着壁板温度的升高,壁板颤振等效应力是逐渐降低的,而且壁板极限环振荡下等效应力水平总体较低,均没有达到各温度下复合材料的屈服极限。
