基于轴对称内聚力单元的立贮发动机黏接界面结构完整性分析*
2022-04-06王君祺鲍福廷崔辉如
王君祺,鲍福廷,崔辉如
(1. 西北工业大学 航天学院, 陕西 西安 710072; 2. 陆军工程大学 国防工程学院, 江苏 南京 210007)
固体火箭发动机依靠结构简单、使用操作便捷和可靠性高的特点,被广泛用作火箭弹、导弹和探空火箭的发动机,以及航天器发射和飞机起飞的助推装置[1]。
反应速度快、杀伤力强、命中精度高、服役时间长、控制范围广以及安全性高将导弹的设计和研发提到了前所未有的高度。其中,安全性能高是一切指标的基础,也是制约导弹性能提升的关键。导弹长期处于战备状态,受发射环境的限制,发动机需要长期处于竖直存放的状态,发动机黏接界面的力学性能将面临严峻的考验[2-6]。黏接界面的脱黏效应将直接导致发动机燃面的变化,使得发动机的内弹道特性偏离初始的设计。
不少研究人员针对发动机黏接界面上的应力情况开展了一系列的研究。韦震等[7]利用内聚力单元并结合双线性的内聚力本构关系,研究了推进剂和绝热层黏接界面的Ⅰ型断裂力学行为。类似的方法同样应用在推进剂/衬层Ⅰ型[8]以及Ⅱ型界面[9-11]。Zhou等[12]利用内聚力单元建立了衬层的有限元模型,研究了发动机中推进剂/绝热层界面间的应力奇异特性。马晓琳[5]通过二维平面内聚力单元构建了绝热层和推进剂黏接界面的有限元模型,研究了发动机受波浪载荷以及点火增压状态等典型工况下黏接界面的力学响应。考虑到结构的轴对称特性,平面内聚力单元处理轴对称问题是不合适的。
本文从轴对称内聚力单元的参考坐标系出发,依次推导了单元的分离位移、内力矢量以及单元刚度矩阵。采用旋转体分离测试,验证单元的准确性。开展立贮发动机黏接界面的结构完整性分析。
1 轴对称内聚力单元
1.1 单元位移变换矩阵推导
如图1所示,在ROZ平面内建立一个初始厚度忽略不计的轴对称内聚力单元,与之相连接的实体单元为四节点轴对称单元。
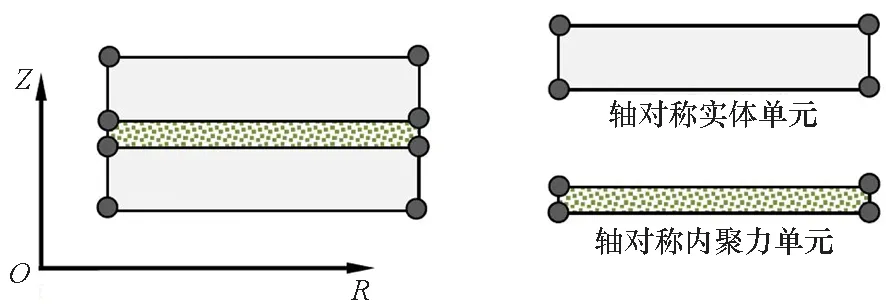
图1 轴对称内聚力单元Fig.1 Axisymmetric cohesive element
图2给出了变形后的轴对称内聚力单元。在单元中线方向设立横轴,过中线的中点垂直于中线的方向为纵轴建立变形后内聚力单元参考坐标系。

图2 变形后的轴对称内聚力单元Fig.2 Axisymmetric cohesive element after deformation
单元节点位移在全局和参考坐标系中的关系满足
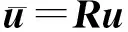
(1)

(2)

(3)
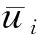

(4)
(5)

1.2 单元分离位移场推导
针对零厚度单元的情况,节点1和节点4以及节点2和节点3是分别重合的,如图3所示。轴对称内聚力单元在变形后的分离位移分别为
(6)
其中,Δ1和Δ2为中线左端点(节点1和节点4)的径向分离位移以及法向分离位移,Δ3和Δ4为中线右端点(节点2和节点3)的径向分离位移以及法向分离位移。

图3 参考坐标系中的分离位移示意Fig.3 Diagram of separation displacement in the reference coordinate
利用矩阵形式可以表示为
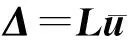
(7)
式中,
Δ=[Δ1Δ2Δ3Δ4]T
(8)
利用一维等参元理论,建立分离位移场与节点分离位移之间的关系,即

(9)
建立中线上分离位移场与节点整体位移间的关系,即

(10)
1.3 单元内力矢量及单元刚度矩阵推导
依据虚位移原理,有
(11)
式中:E和S分别代表格林应变张量和第二PK应力张量;Δ和Tc分别代表分离位移以及内聚力,Γc是指单元中线;Text以及u代表外力以及节点位移矢量,Γ为整个单元所围成的区域。
结合伽辽金法和等参元理论,推导可得单元的刚度矩阵以及内力矢量分别为
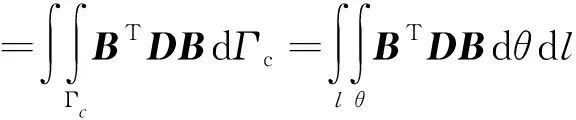
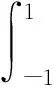
(12)

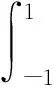
(13)
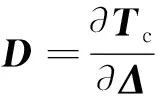
2 验证算例
2.1 旋转体模型
图4给出了一个轴对称柱状旋转体的子午面示意图,旋转体的内外径分别为2 mm和4 mm,高为4 mm。沿着子午面的中心与水平方向呈45°的位置存在贯穿整个板的黏接界面。旋转体的底部固支,顶部施加竖直方向的位移载荷。本验证算例中,位移的拉伸速率为0.1 mm/s,在达到指定位移1 mm时开始松弛40 s。旋转体的杨氏模量以及泊松比分别为10 MPa和0.33。本算例中,除了利用轴对称单元对结构进行建模,还采用不同环向单元数量的三维网格进行对比分析,其中环向网格的数量分别为6、18以及54。
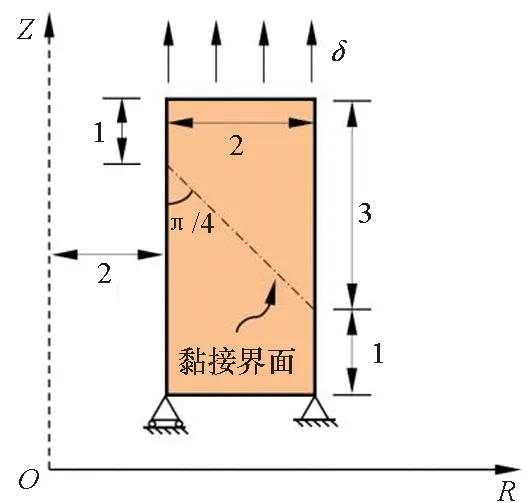
图4 旋转体子午面Fig.4 Meridian surface of the rotating body
2.2 黏弹性内聚力模型
PPR内聚力模型是Park等提出的考虑物理断裂参数以及连续断裂边界的势相关内聚力模型[13],该模型的势函数表达式为
(14)
式中:Γn和Γt为能量常数;m和n为无量纲参数;αk和βk为模型的形状参数,分别控制法向和切向的内聚力和分离位移曲线下降段的凹凸特性;δn和δt为模型的法向和切向的临界位移;φt和φn分别代表切向和法向内聚能,其表达式为
(15)
σmax和τmax代表法向和切向内聚强度。
Cui等[14]提出了基于参数松弛的黏弹性PPR内聚力模型,其具体形式为
(16)
黏接界面初始内聚强度σmax和τmax、初始临界位移δn和δt、初始无量纲参数m和n分别为0.5 MPa、0.5 MPa,2.5 mm、2.5 mm,0.167 2以及0.167 2。形状参数αk和βk均为3.10,黏弹性系数u=0.3,τ=50 s。
2.3 仿真结果分析
图5表示不同模型在加载阶段的径向和轴向的支反力随时间的变化趋势。由图5可以明显地看到,三维模型的结果曲线随着网格规模的不断增加,逐渐收敛于轴对称模型的分析结果曲线。仿真结果表明,构建的轴对称内聚力单元是准确的。

(a) 径向(a) Radial direction
图6给出了四种有限元模型总的自由度、单元数以及计算耗时的情况。为了比较方便,这里假设轴对称模型的自由度、单元数以及计算耗时都为单位1。可以明显地看到,随着环向网格数量的增多,三维模型的自由度、单元数以及计算耗时剧烈增加。尤其是当环向的网格数量增加到54个的时候,三维模型的自由度和单元数是轴对称模型的300多倍,而三维状态下的耗时甚至达到了轴对称模型的600多倍。以上分析结果表明,采用轴对称内聚力单元计算模型是经济高效的仿真手段。

图6 计算模型对比Fig.6 Comparison of computational models
3 立贮发动机黏接界面的力学性能研究
3.1 发动机有限元模型
对立贮式发动机在长时间贮存状态以及受到轴向过载时的结构完整性进行分析是进行轴对称内聚力单元开发的主要任务之一。图7所示为某发动机简化后的轴对称几何以及部分有限元网格模型。发动机整体长度为630 mm,推进剂和绝热层部分的长度为570 mm,其中,圆管段、翼槽段以及星孔段的长度分别为300 mm、43 mm和227 mm。圆管段和星孔段推进剂的厚度分别为73 mm和48.5 mm,绝热层和壳体的厚度分别为2 mm和3 mm。此外,由于涉及轴对称计算,发动机中轴线和各部位的相对位置如图7所示。为了简化网格规模并保证计算精度,在远离黏接界面处采用稀疏的网格规模,在黏接界面两侧对网格进行加密。推进剂、绝热层以及壳体内聚力单元的材料属性和文献[15]一致。

图7 发动机轴对称模型Fig.7 Axisymmetric model of solid rocket motor
图8所示为发动机在点火上升阶段受到的三种轴向加速度变化曲线,假设加速时间为200 s。
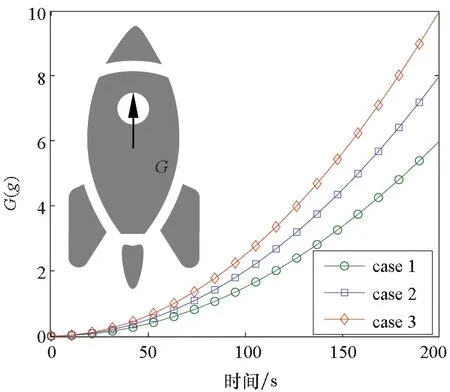
图8 轴向加速度示意Fig.8 Diagram of axial acceleration
3.2 轴向加速度影响分析
发动机黏接界面应力分布如图9所示,切向内聚力在黏接界面上的分布差异较大,加速度因子的增加会提升界面上切向内聚力的整体水平。切向内聚力在黏接界面的两端会出现突变,这与黏接界面两端受到直接的约束有关。此外,在翼槽段的两侧,翼槽段与圆管段和星孔段过渡的地方可以看到明显的内聚力改变。对于法向内聚力而言,由于向上的加速度作用,惯性力在发动机的尾部集中,因此,在黏接界面的底部,法向内聚力达到了最高水平,并且随着加速度因子的增加而加剧。在圆管段和星孔段,法向内聚力水平较低。尤其在星孔段,部分黏接界面处的法向内聚力已经接近于零,加速度因子在这些部位的影响较小。在翼槽段,由于黏接界面两侧变形的不协调,法向内聚力有轻微的增加,但是相比于黏接界面的底部,这部分的法向内聚力仍处于较低水平。与切向内聚力类似,加速度因子的增加会提升界面上法向内聚力的整体水平。

(a) 切向(a) Tangential direction
3.3 波浪载荷影响分析
舰载导弹在服役期间需要长时间受到海上波浪的影响,考虑到舰船空间有限以及为减少导弹的发射准备时间,发动机往往需要竖直存放在发射筒内。因此,海面上的波浪载荷将直接作用在黏接界面上。
一般而言,波浪载荷对舰船的影响可以分解成三个方向的振动,沿着船艏方向的纵摇、沿着左舷方向的横摇以及垂直方向的垂摇。考虑到轴对称模型特定的使用环境,这里仅分析对黏接界面影响较为恶劣的垂摇。研究表明,舰船的振动曲线和浪级(海况级数)之间有着一定的关联。舰船垂摇随海况级数之间的关系为
az(ti)=Δaz[1+kz(l-2)]sin(2π·fz·ti)
(17)
式中:az(ti)表示ti时刻的垂摇加速度;Δaz为垂摇的加速度幅值,Δaz=rand(100 mm/s2,1 000 mm/s2);kz为加速度放大系数,kz=0.24;l为海况级数,fz为ti时刻竖直方向的波浪频率,fz=rand(0.1 Hz, 1 Hz)。
图10给出了不同海况级数下,发动机黏接界面上最大的切向和法相内聚力随着时间的变化。

(a) 切向(a) Tangential direction
从分布上看,随着海况级数的提高,出现高水平内聚力极值的可能性越大。和点火发射时的过载作用相比,波浪作用产生的切向内聚力表现得十分微弱。但是,这也从另一个方面说明,波浪作用下,黏接界面在切向上是比较安全的。
图11给出了不同海况下,切向内聚力和法向内聚力极值出现部位随时间的变化曲线。可以发现,极值出现的位置无一例外地都分布在黏接界面的两端。这说明,在波浪载荷引起的垂向加速度的作用下,黏接界面上接近发动机头部和尾部的位置是需要着重分析和加固的。另外不难分析,随着海上执勤时间的延长,黏接界面上的损伤会逐渐累积,从而引起黏接界面的局部开裂等严重危害。

(a) 切向(a) Tangential direction
4 结论
本文研究了轴对称内聚力单元在立贮发动机黏接界面结构完整性分析中的应用。通过构建参考坐标系的形式,建立了单元节点位移和单元内力以及单元矩阵之间的联系。利用三维以及轴对称网格分别开展旋转体的分离试验,计算结果表明,轴对称内聚力单元可以准确和高效地进行轴对称问题的仿真模拟。开展了立贮发动机在轴向加速度以及波浪载荷下,黏接界面的力学响应分析。仿真结果显示,加速度因子和海况级数的提高会提升界面上内聚力的整体水平。内聚力极值分布在黏接界面的两端,在设计阶段需要重点关注。
致谢
延世大学Kyoungsoo Park(朴景秀)副教授在轴对称内聚力单元推导方面提供了很大的帮助和指导,谨致谢意!
