采用弹道修正技术的红外干扰弹性能优化*
2022-04-06邢炳楠杜忠华杜成鑫
邢炳楠,杜忠华,杜成鑫
(南京理工大学 机械工程学院 智能弹药技术国防重点学科实验室, 江苏 南京 210094)
现代战争中,红外干扰弹作为一种有效的红外对抗手段,能够抑制、干扰、削弱、破坏红外干扰系统的正常工作,使其探测能力下降、跟踪目标失败[1]。通过引导红外导弹偏离原有轨迹使其脱靶,这对保证飞机安全,提高其生存水平意义重大。如何提高红外干扰弹的干扰效能,已成为该领域研究的重要问题。弹道修正技术通过对制式弹药进行模块化改造,可以低成本实现对干扰弹飞行弹道的修正,该技术是目前智能弹药领域研究的热点之一。通过将弹道修正技术应用于红外干扰弹,可根据任务需要进行弹道修正,从而保持与飞机的合理距离,提升红外干扰弹对飞机伴飞效果。
脉冲式修正机构作为智能弹药领域一种主要的弹道修正手段,具有响应时间短、反应速度快、环境适应性强以及易于全弹结构优化等优点[2]。考虑到红外干扰弹的有效作用时间,脉冲式修正机构适用于对传统红外干扰弹进行技术改造。从工程角度来看,与常规制式弹药不同的是,安装修正机构的干扰弹设计在面对特殊的工程约束、有限的设计空间时会影响执行机构的修正效率。此外,弹丸高度非线性的动力学特性导致控制难度的增加。然而传统方法在进行武器系统设计时,由于涉及的变量较多,主要从最初的概念开始,设计的各种特征以逐步的方式改变,从而改进给定的性能标准,直到满足要求。但是通过顺序迭代对气动外形、结构以及控制系统进行设计时,在时间、效率和设计精度上已经不能满足研制要求[3]。尤其是当设计对象为需要与修正技术结合的红外干扰弹时,这种渐进式、串联式的设计方法不再适用,无法得到相应的全局最优解。基于实验设计(Design Of Experiments,DOE)和响应面(Response Surface Methodology,RSM)等更为现代的设计过程更为合适。这些方法为多变量设计提供了理论框架,当与适当的优化算法相结合时,可得到设定性能准则下的全局最优设计[4]。
DOE和RSM除在许多航空航天系统中都得到了广泛的应用外,在基于弹道修正技术的智能武器设计领域也有少量研究。Schönning等[5]在空对空导弹的概念设计阶段,面对其高耦合、涵盖多学科的设计特征,利用DOE及RSM方法为工业类型的设计优化提供了新思路。Won等[6]针对高速导弹的气动性能优化问题,利用RSM方法有效缩短了优化方案的设计周期,并证明所提方案对于武器系统在初步概念设计阶段,大规模分析问题的应用价值。尽管文献[5-6]的设计目的是为了在设计空间进行插值,但最终并未对其结果进行性能评估。王波[7]则将基于Kriging的RSM方法应用拓展至随机空间,提高了该方法对于处理不确定性问题的能力。这为本文提高模型预测的精确度提供了研究思路。而Lee等[8]指出DOE及RSM方法在设计空间和目标函数相关时,针对所提供代理模型的不足,并提出了将多目标遗传优化算法和神经网络相结合的可行性设计方案。尽管这些智能优化方案在智能武器的设计中得到了一定程度的关注,但对于本文的研究对象而言,独特的工程设计及稳定性约束,增加了设计方案的难度,同时带来额外的设计难题。
本文以基于修正技术的红外干扰弹为研究对象,提出了一种基于DOE和RSM的性能设计优化方案。尽管干扰弹的总体性能设计涉及的因素和学科很多,但本文中只关注关于其修正执行机构以及气动外形方面的优化。通过拉丁超立方实验设计和6自由度(Degree Of Freedom, DOF)刚体弹道模型进行DOE设计,同时纳入随机因素考量,建立随机克里金(Stochastic Kriging,SK)代理模型,实现对空间设计点的性能预测。此外,为实现对设计空间中生成的不稳定弹道的识别,设计了一个神经网络分类器。在最后的设计阶段,利用多种群遗传算法(Multiple Populations Genetic Algorithm,MPGA)[9]分析优化目标下的全局最优解。同时,通过改变代价函数权重的方法研究基于弹道修正技术红外干扰弹的Pareto优化方案。
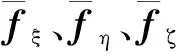
1 红外干扰弹设计优化建模
1.1 总体设计优化过程
如图1设计优化流程图所示,在设计优化过程中,第一步通过拉丁超立方抽样[10-11]和6DOF弹道方程,建立DOE数据库。考虑到概念设计阶段主要借助计算机仿真进行研究,因此,本节利用DOE方法的一个分支——计算机实验法(Design and Analysis of Computer Experiments,DACE)高效地实现在设计空间的填充,提供设计点的优化分布[12-13]。首先定义某红外干扰弹为基础设计模型,同时,对ND个设计变量D={D1,D2,…,DND}进行定义并给出范围,设定NP项性能评价准则P={P1,P2,…,PNP}。根据设计空间样本点进行6DOF弹道仿真完成基于DACE的数据获取。
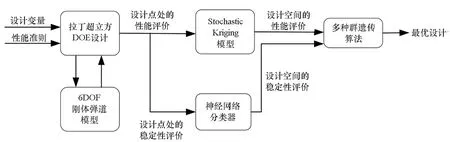
图1 基于弹道修正技术的红外干扰弹设计优化过程流程图Fig.1 Flow chart of design optimization process of infrared interference decoy based on trajectory correction
设计过程的第二步是建立SK代理模型。其主要目的是建立设计变量与性能准则之间的映射关系,在不运行6DOF弹道模型条件下实现对弹道性能的快速预测。与传统Kriging方法不同的是,SK模型引入不确定性因素,有利于后期进一步的稳健性优化设计[14]。具体模型表达与文献[15]保持一致。
不合理的参数配置可能会导致弹丸失稳,尽管SK模型可以快速地对弹道性能进行评估,但其无法对生成的不稳定弹道进行识别。因此在第三步设计过程中,通过设计一个两层的前馈神经网络分类器实现不稳定设计的辨识。
优化设计过程的最后一步,根据任务目标,利用MPGA算法得到最优设计[16]。同时,通过连续改变代价函数中的权值,可以得到一组Pareto最优解,以说明最优设计如何随着目标函数在弹丸性能之间的取舍而改变。对于设计空间D∈RND,MPGA的设计优化问题可以表达为:
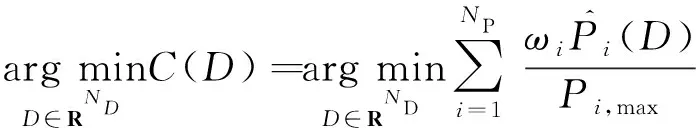
s.t.N(D*)>T*
(1)
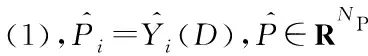
1.2 红外干扰弹动力学模型
为对可弹道修正的干扰弹在设计参数变化下的性能进行模拟仿真,首先定义文献[17]中的制式基准榴弹结构和相关的有控6DOF弹道模型。弹丸整体弹重m为5.23 kg,质心距头部约228.34 mm,极转动惯量A约为3 874.54 kg·mm2,赤道转动惯量C为52 342.9 kg·mm2。值得注意的是,由于脉冲作用时间较短,因此可在设计过程中忽略修正机构之间的相互气动作用。此外,本文中设置脉冲发动机全部使用完毕为修正任务结束。
在DOE设计阶段使用文献[17]中标准的6DOF动力学模型,则干扰弹的运动微分方程如下:
(2)
其中
(3)
(4)
则脉冲控制力分量的等效平均值表达式为:
(5)
(6)
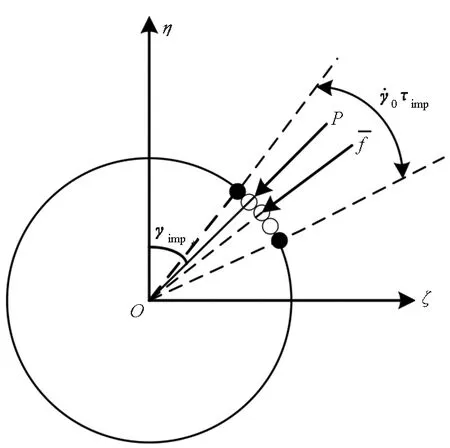
图2 瞬时脉冲控制力与等效平均脉冲控制力的关系Fig.2 Relationship between instantaneous pulse control force and equivalent average pulse control force
2 基于弹道修正技术的红外干扰弹优化设计实例
2.1 基于弹道修正技术的红外干扰弹设计问题定义
考虑到干扰弹对飞机的伴飞任务,首先要求修正弹道的射程尽可能最大,其次需要尽可能最小化弹道攻角和脉冲发动机能耗。但在设计过程中对于这三项性能准则,并不要求它们之间严格互斥。设在一定脉冲参数配置下,修正弹的射程表示为R(D),修正弹道的最大攻角表示为A(D),总的脉冲发动机能耗用I(D)表示。则对于本文的优化问题,则代价函数表达形式如下:
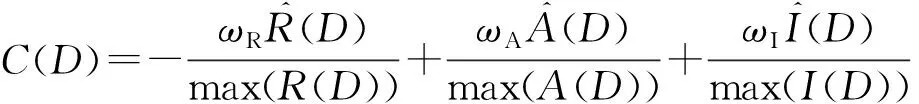
(7)
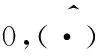
对于红外干扰弹,具体的设计变量及其取值范围如表1所示,共有7个连续变量,1个离散变量。在拉丁超立方设计过程中,连续变量被离散化,但在SK模型拟合和MPGA优化过程中保持连续性。
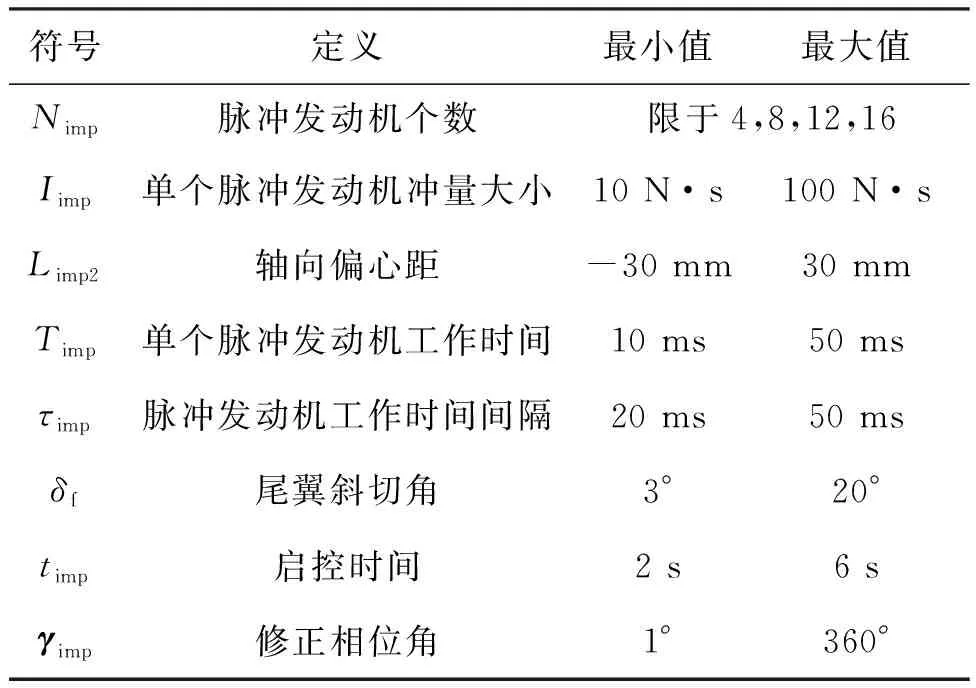
表1 优化问题设计变量示例
由于本文的基础模型为低旋尾翼稳定弹,要实现一定方向的弹道修正,必须要求弹体具有一定的转速,其转速的产生主要由尾翼导转力矩和滚转阻尼力矩的动态平衡产生[18]。因此,转速的设计对于修正机构性能有重要影响。在本文研究中,对于弹丸转速的性能优化主要通过尾翼斜切角的设定实现。
2.2 实例优化结果
对于本文中的干扰弹仿真条件,假设飞机以238 m/s速度在6 km高空水平直飞,干扰弹以30 m/s速度垂直飞机机身向上发射。根据表1中的8个设计变量,通过拉丁超立方实验设计和6DOF弹道方程产生732条模拟弹道。图3中表示了三种不同参数设计下弹丸的性能体现,图4则展示了三种设计中修正弹攻角随时间的变化曲线。在DOE设计中,通过设定三条性能评价准则,并建立对应性能准则下的三个Stochastic Kriging模型。由于SK模型会精确拟合用于构建模型的DOE数据,因此除去用于进行建模的732条弹道外,另有一组弹道数据用于进行模型预测精度优劣的评价。此外,在SK建模仿真过程中,通过尝试不同的回归函数选择,根据拟合效果,最终以二阶多项式和球形相关模型进行回归函数的相关设计。
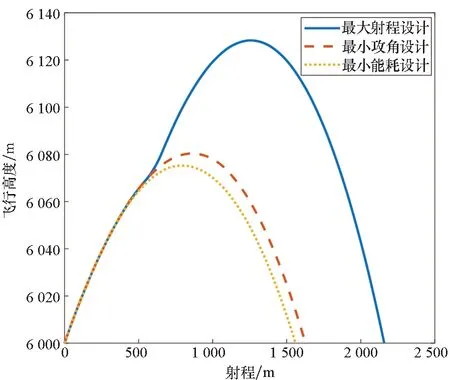
图3 射程-飞行高度弹道轨迹示例Fig.3 Altitude versus range for example trajectories
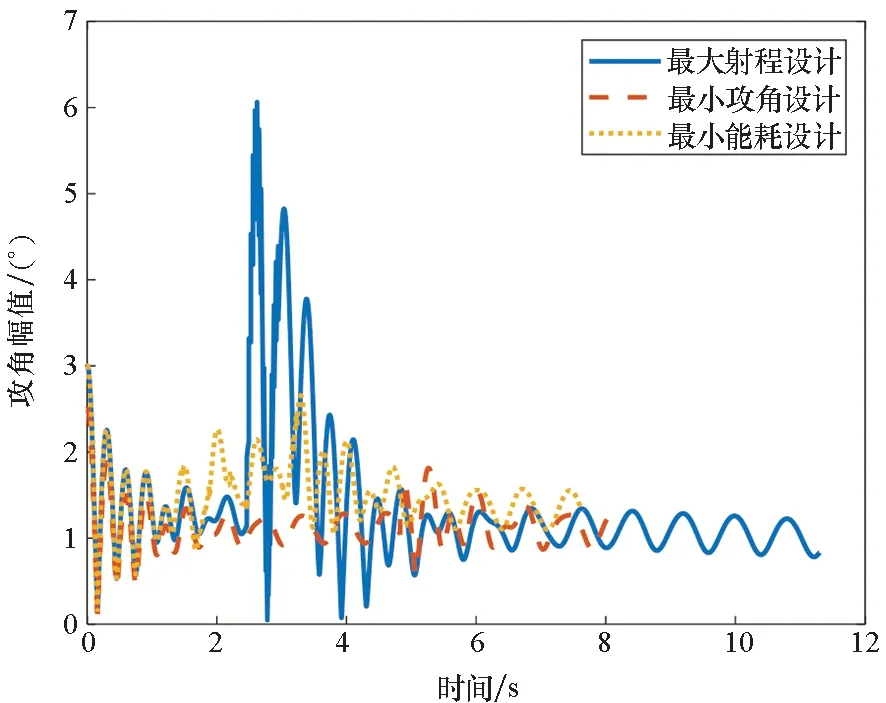
图4 设计实例中攻角-时间关系示意图Fig.4 Total angle of attack versus time for example trajectories
图5是DOE数据中不同设计参数下有关弹道的射程和最大攻角的仿真结果,数字代表不同的修正机构个数。由图5可知,更大的射程设计对应更大的最大攻角幅值。结合外弹道学理论及6DOF弹道仿真分析可知,过大的攻角幅值是由不合理的尾翼斜切角设计及过大的脉冲作用导致的,这可能会造成弹丸的飞行失稳。一定程度的转速提高可以提高修正效率,增大修正距离,但是也可能会导致弹丸的不稳定[19]。因此,在优化设计中,需要更好地平衡各参数之间的关系。图6则是相同的DOE数据中关于射程和脉冲发动机总冲量的结果。可以看出,更高的能耗并不意味着更大射程,最终的射程是由多个因素(比如单个脉冲发动机持续时间)决定的,这允许在实际工程设计中选择能耗更低的方案降低制造成本,进一步体现基于低成本弹道修正技术对红外干扰弹改造的优势。在拉丁超立方的实验设计点中,存在一些点生成了不稳定的弹道设计。根据设计变量的选择,这种不稳定设计可能是由过大的尾翼导转力矩或者过大脉冲修正力矩造成的。尽管自身低旋尾翼弹的攻角可在静力矩作用下进行一定程度的衰减,但为尽可能保证设计稳定性,本研究中对超出稳定性判别标准的设计进行剔除。
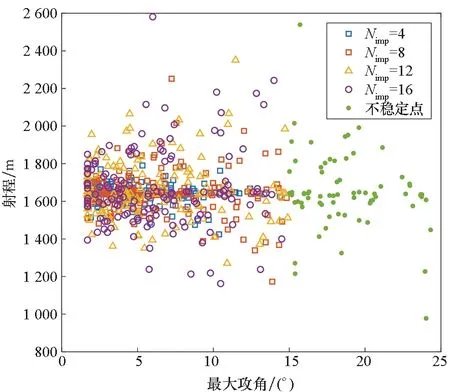
图5 拉丁超立方体DOE数据(最大攻角-射程)Fig.5 Latin hypercube DOE data (with respect to maximum angle of attack and range)
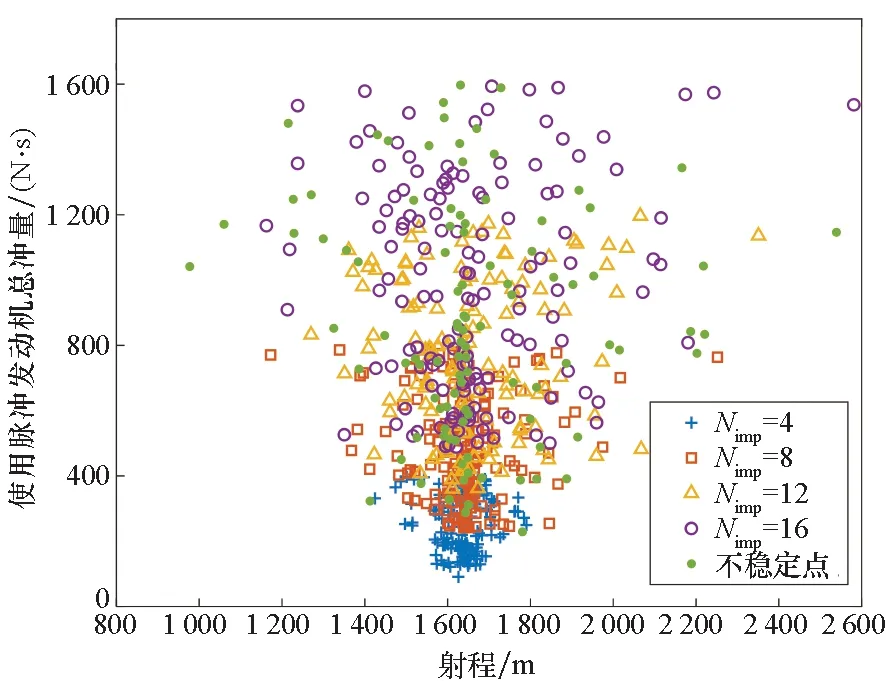
图6 拉丁超立方体DOE数据(射程-脉冲发动机总冲量)Fig.6 Latin hypercube DOE data (with respect to range and total impulse of pulse thrusters)
利用与构建SK模型不同的另一组数据(该组数据同样包括732条弹道,但为清晰显示预测结果,仅选择150条结果进行分析)对所建立的模型预测性能进行评估,结果如图7所示。可以看出,所构建的SK模型对于该组数据的预测结果绝大部分吻合于6DOF仿真结果,对于个别设计点存在较大误差。此外,相比于普通Kriging建模,SK模型涵盖不确定信息后,其预测均方误差大,可有效降低不确定因素的影响,使得设计弹药在这些因素影响下仍能保持性能稳定和安全可靠。
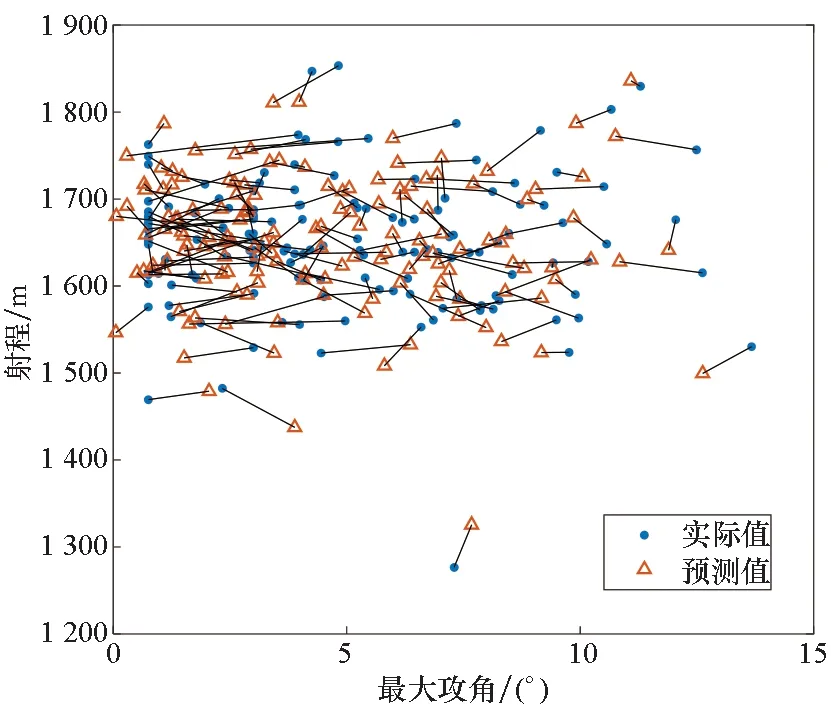
(a) 最大攻角-射程(a) With respect to maximum angle of attack and range
对于造成不稳定弹道的设计,可以通过一个两层的前馈神经网络模型实现。DOE数据中,70%被用于进行网络训练,15%用于校验,15%用于测试[20]。由于本文在人工神经网络(Artificial Neural Network, ANN)设计时选择Sigmoid函数作为神经元的激活函数,因此仿真中选择交叉熵代价函数作为训练程度的评判。当交叉熵误差值达到最小值时,则认为该ANN训练完成。图8表示ANN训练过程中交叉熵成本函数的变化,从图中可看出,19周期时得到最佳验证性能,大小为0.037 9。本仿真实例中,在19轮训练周期后得到了训练好的ANN。为进一步对其分类准确性进行评估,使用另一组的732条弹道数据进行神经网络进一步测试,如图9、图10所示。对ANN的输出值N(D)进行从低到高排列,对其编号后的结果如图9所示。然而,可以看出,在稳定性分类结果中约有1%呈现假阳性判断,即实际上不稳定的弹道设计被误判为稳定。如图10所示,可以看出,在设定输出层阈值为0.8时,假阳性概率可以达到5%以下。值得注意的是,较高的假阴性同样影响分类器性能,因为MPGA可能会排除这些被误判不稳定的区域。实际设计过程中,阈值选择需要根据综合衡量假阴性及假阳性概率后确定。整个优化过程的实现是通过调整目标函数中权值大小实现的,图3、图4中给出了三种边界情况的优化设计实例。此外,给出另外四种性能折中方案,具体结果如表2、表3所示,基于不同的设计目标,调节权重,提供每组设计参数的最佳折中方案。例如,对于折中设计Ⅰ,设计目标需要在尽可能增大射程的同时最小化攻角,但不要求能耗最低,因此可适当增加修正机构个数,减小单个脉冲冲量大小,提早修正时间来实现任务目标。
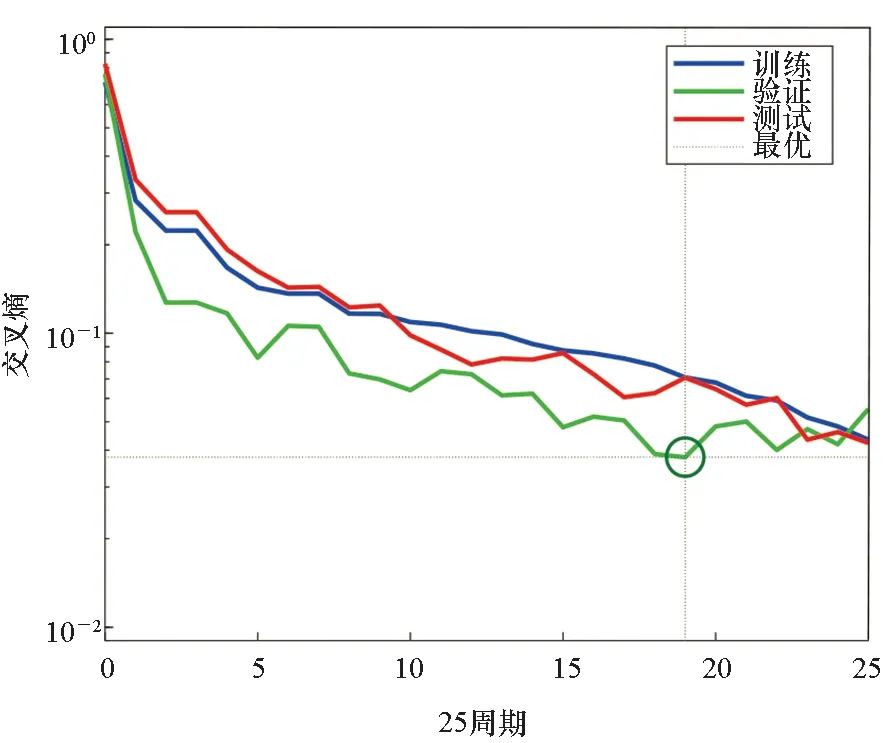
图8 神经网络训练结果Fig.8 Neural network training results
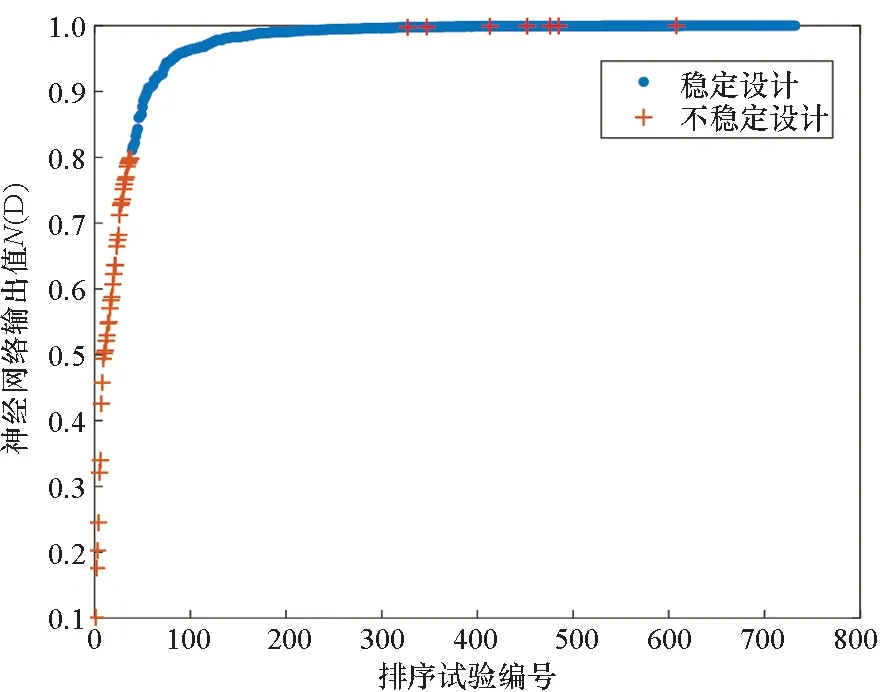
图9 数据验证集(6DOF模型)的神经网络分类结果Fig.9 Neural network classification results for validation set of 6DOF data
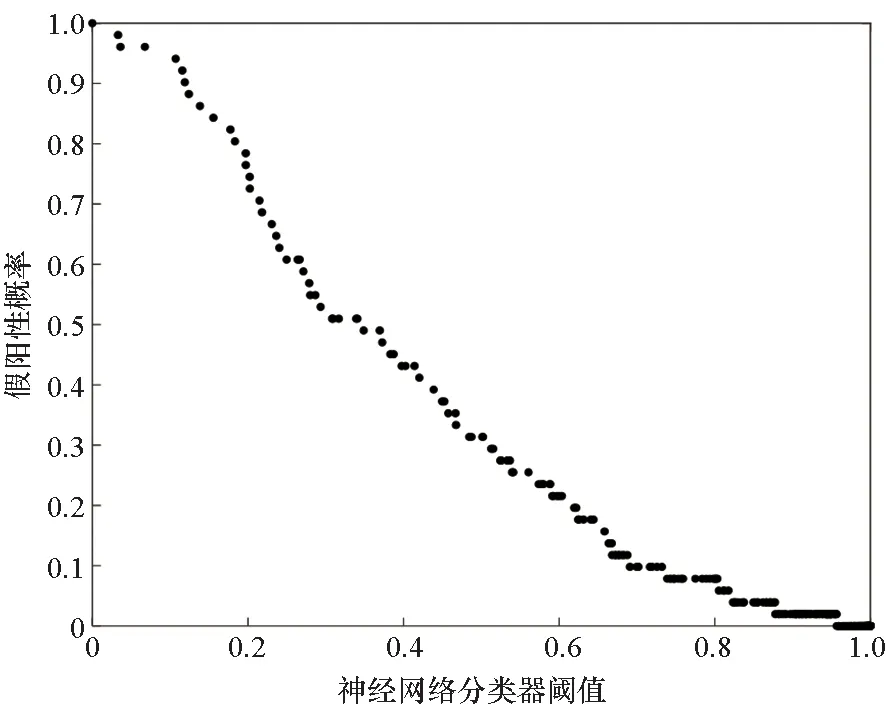
图10 神经网络分类器的阈值与误报概率的关系Fig.10 Threshold value versus probability of false positive for neural network classifier
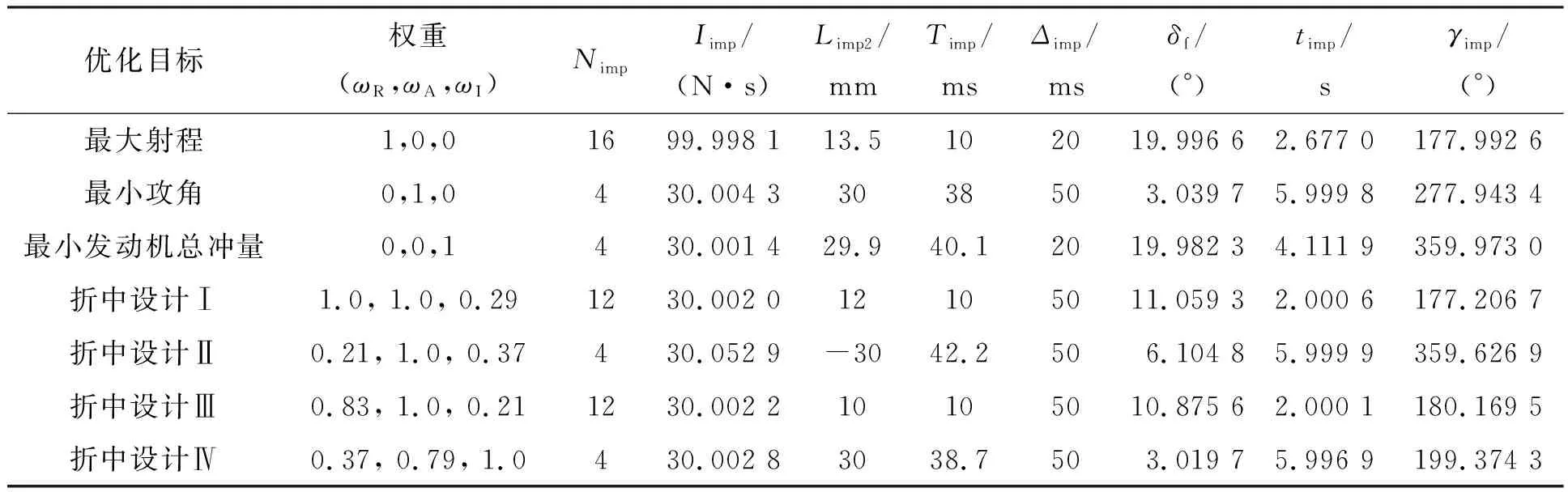
表2 不同目标函数权重的优化设计配置
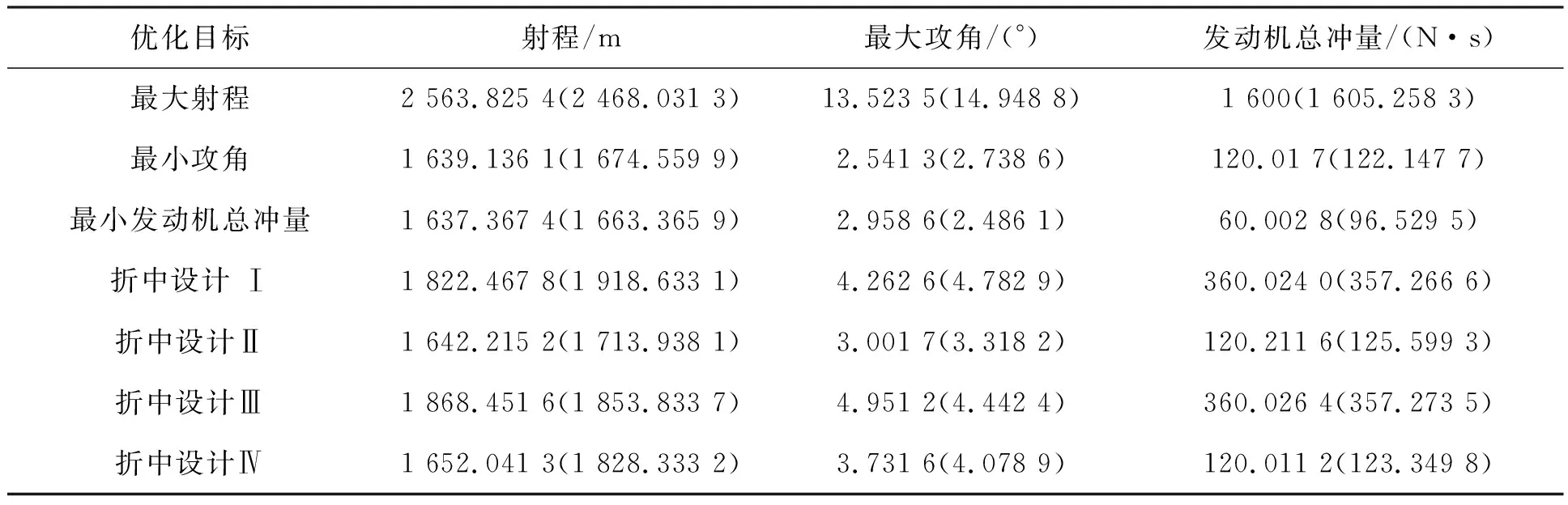
表3 不同目标函数权重下优化参数配置的模拟(预测)性能
2.3 Pareto前沿设计
Pareto最优设计被定义为一种设计配置,在不牺牲至少一个其他指标性能的情况下,一个性能指标的改进是不可能的。所有Pareto最优设计的集合称为Pareto前沿[21]。对于可弹道修正的干扰弹的工程设计而言,Pareto前沿可以通过确定一组设计代表目标函数中性能准则之间的最佳权衡。实际仿真设计中,通过连续改变目标函数中权值变化得到Pareto前沿。Pareto前沿展示了最优设计如何随着任务目标的变化而变化,并代表了各种任务目标之间的最佳权衡(给定选定的权重因子)。如果成本函数包含了与配置选择相关的所有因素,那么设计者应该从中选择最优设计[22]。
如图11所示,通过连续改变权值大小,得到设定指定性能准则下的Pareto设计集,图中优化参数配置的性能预测通过6DOF仿真得到。通过与初始的DOE数据比较可得,所得Pareto最优解基本落于拉丁超立方实验样本边缘,这表明通过优化参数配置在设定指标上得到了改善。同时设计集中的点表示,通过合理权衡参数设计,可在尽可能最小化攻角及脉冲能耗的条件下得到更大的射程。
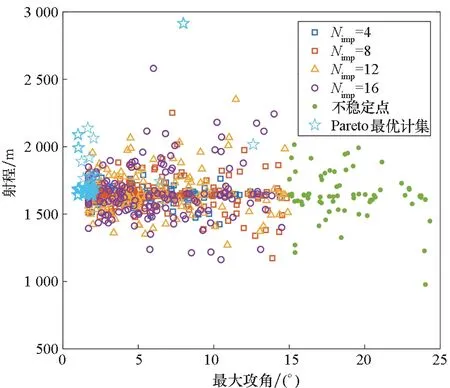
(a) 最大攻角-射程(a) With respect to maximum angle of attack and range
总体而言,本研究的仿真结果证明了所提优化方案在工程应用中将武器概念设计阶段的期望任务目标和性能要求转化为一组确定的最佳设计的实际意义。特别是对于优化过程中给出的Pareto前沿,对于更好地理解设计方案以及创建可行的设计集具有重要意义。值得注意的是,本文所提出的算法计算负担较小。该方法较低的计算负担可使重复该设计过程较为轻松,这对于概念设计阶段的脉冲修正弹而言十分重要。同时,该方法具有良好的可移植性,对于其他智能武器的设计同样可以借鉴。
3 结论
本文以某红外干扰弹作为设计基础,对采用基于弹道修正技术的红外干扰弹的性能优化进行了研究,并提出了一种基于DOE和RSM的优化算法。该方法的一个特点是使用了考虑设计变量随机性的Stochastic Kriging模型进行拟合预测,与传统Kriging方法相比,这可以保证设计方案具有一定的稳健性。此外,文中给出了一个概念设计阶段关于干扰弹的设计实例问题。研究结果表明,通过对性能标准的折中,可以产生一组代表最优设计集的Pareto前沿。总的来说,一方面,在概念设计阶段,文中所提出的方法可保证弹道修正技术成功实现对红外干扰弹的技术改造,使得伴飞任务成功完成时更具机动性;另一方面,该方法表现了智能武器设计过程正在从传统的串行设计向更现代化、智能化的转变。
