基于多核模糊C均值聚类的配电网短期负荷预测
2022-04-06孙景钌胡长洪项烨鋆刘津源陈梦翔蔡昌春
孙景钌,胡长洪,项烨鋆,赵 碚,刘津源,陈梦翔,蔡昌春
(1.国网浙江省电力有限公司温州供电公司,浙江 温州 325000;2.江苏省输配电装备技术重点实验室(河海大学),江苏 常州 213022)
0 引言
电力系统短期负荷预测是电力系统运行与调度的基础,预测精度直接影响电力系统运行的安全性和经济性。影响负荷波动的因素众多,其中气象因素尤为重要[1-2],气象因素直接影响用户用电习惯从而导致负荷波动。因此,从负荷波动的机理出发,分析气象因素对负荷变化的影响对于提高短期负荷预测精度具有重要意义。
近年来,国内外学者针对负荷预测及影响因素开展了大量的研究工作。文献[3]针对通过可视化降维方法解决负荷预测中高维气象数据的拥挤和结构易变问题,从而提高负荷预测精度。文献[4-5]利用费歇信息进行气象因素建模,挖掘负荷-气象因素关联性使得负荷预测中气象因素的处理更加客观。文献[6-8]通过分析母线负荷与气象因素相关特性,创建了基于数值天气预报和负荷分类预测的母线负荷预测模型,并提出了基于气象预报的母线负荷预测方法,但是对于气象因素没有给出明确的划分和选择方法。
为了更加精准描述气象因素对负荷预测的影响,聚类分析法常常被用来提取数据样本特征以分析气象因素的影响[9-12]。文献[13]针对多类样本数据提出多核模糊聚类算法,选取子核函数及其参数用于构造多核函数,从而增大不同类别样本间的差别。文献[14]提出了一种电力短期负荷场景中改进多核模糊C 均值聚类算法,提升预测聚类能力,但是在核函数各参数选择偏于经验。
人工智能、深度学习方法能够充分挖掘负荷变化的本质特征,其在负荷预测领域的应用越来越广泛。文献[15-16]提出了一种GRU-NN(门控循环单元神经网络)的短期负荷预测方法,通过建模学习负荷数据内部动态变化规律,融合天气影响因素分析负荷变化的内在联系。文献[17-18]提出了在LSTM(长短期记忆)神经网络中采用Attention 机制进行输入特征分析,提高历史训练数据特征的可辨识性。文献[19-20]利用改进深度系数自编码器和极限学习机结合的方法进行短期负荷预测,实现气象因素的稀疏处理和低维压缩编码。然而,传统LSTM 神经网络在负荷预测中往往存在误差累计现象,从而影响预测精度。
本文针对复杂气象因素下负荷预测困难的问题,分别从负荷数据处理和预测方法两方面开展工作。提出了基于多核C 均值模糊聚类的负荷影响因素聚类压缩,利用核函数提取影响负荷波动的气象因素动态特征;在传统LSTM结构的基础上,引入反馈环节,利用正反向计算结合消除LSTM神经网络训练过程的累计误差,提出基于深度学习的多层双向LSTM 神经网络负荷预测模型,由此提升负荷预测精度。最后,以历史负荷的聚类数据为训练样本验证本文方法的有效性和合理性,实验结果表明本文方法能够充分考虑历史负荷数据中的气象因素特征,提高负荷预测的准确性。
1 基于多核模糊C 均值聚类的负荷气象影响分析
1.1 负荷气象因素关系
影响负荷波动的气象因素较多,实际负荷数据和气象因素间存在强耦合、非线性关系。分析负荷与气象影响因素的相关性是剖析负荷特征的主要方式。斯皮尔曼相关系数法是分析气象因素与负荷相关性的常用方法,可以更直观的看出每一类影响因素对负荷的影响程度,能够精准的刻画变量间的关联程度。斯皮尔曼相关系数法是通过内部重复值来比较内部变量间的单调性,用+1或-1来表示,斯皮尔曼相关系数公式如下所示:

1.2 多核C均值模糊聚类
核函数法是数据特征提取的常用方法,可以弥补单一核方法提取负荷数据特性存在特征描述单一的不足。利用多核函数将气象因素的低维非线性关系转变为高维线性问题从而提高聚类对多维空间数据的聚合能力。在聚类过程中采用基于模糊准则自动调节不同核函数的权重系数,提升组合核函数的特征学习能力和聚类后系统描述的泛化能力。
假设聚类模型样本集为{x1,x2,…,xN},xk∈RN,利用非线性映射函数Φ将低维空间的样本映射到高维特征空间中{Φ(x1),Φ(x2),…,Φ(xN)}。高维特征空间中基本核函数可以用低维空间的点积表示:

在满足Mercer 条件下将多个核函数构造凸线性组合以提高组合核函数的泛化能力,线性组合关系表示为:

式中:Kk为基本核函数;β为不同核函数的权重系数;M为核函数的个数。
利用核函数将负荷数据样本中的气象因素从高维空间向低维空间映射,并提取各种影响因素的特征空间,实现每类样本特征的划分和分类。文中多核C均值模糊聚类的目标函数为:

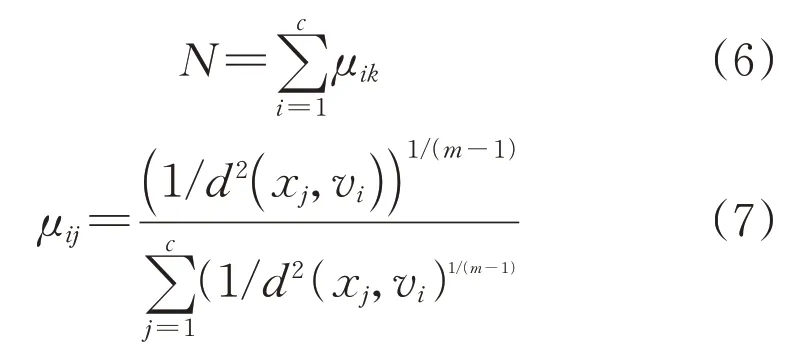
式中:d为第i个样本聚类数据到第j类聚类中心的Euclid距离,由式(8)计算:

聚类中心Φ(Vi)在特征空间H中表示为:

由上述可知,多核模糊C 均值聚类模型聚类过程中需要明确核函数参数值σ、模糊指数m、收敛阈值ε和聚类簇数c等四个参数。通过初始化中心矩阵及隶属度矩阵使其满足归一化条件,利用迭代计算获得最终权重和隶属度,迭代过程的终止条件为隶属度矩阵||U(t)-U(t-1)||<ε。
2 基于多层双向LSTM 神经网络的负荷预测
2.1 双向LSTM神经网络
传统单向LSTM 神经网络模型在短期负荷预测中由于存储历史与当前的信息,导致在训练过程中容易出现累积误差等问题。如图1所示,双向LSTM 神经网络模型输出由两个信息传递相反的LSTM 循环层构成,前向层按照时间顺序传递信息,后向层按时间顺序逆向传递信息。在神经网络训练过程中,分前向训练和后向训练两个LSTM 模块,前向训练输入序列是数据样本,后向训练的输入序列的反向样本,网络的输出由前向输出和后向输出共同决定。

图1 双向LSTM神经网络记忆单元结构
前向层从1 时刻到t时刻正向计算得到并保存每个时刻向前隐含层的输出;后向层逆时间序列反向计算得到并保存每个时刻向后隐含层的输出。最后融合前向层和后向层对应时刻的输出结果,双向LSTM神经网络的表达式为:

式中:st为t时刻的前向隐藏层状态;为t时刻的反向隐藏层状态;ot为t时刻输出层的值;g和f为激活函数;xt为输入向量;V、U、W为隐藏层到输出层、输入层到隐藏层、隐藏层之间的权重矩阵;V′、U′、W′为对应的反向权重矩阵。
2.2 多层堆叠双向LSTM神经网络
在传统双向LSTM 神经网络的基础上构建深度化多层机制和反向反馈机制,强化负荷数据本质特征,避免学习过程中训练记忆的模糊化,减少训练误差。本文提出的多层堆叠双向LSTM 神经网络结构如图2所示,相对单层网络多层堆叠模型能够对早期预测数据加深记忆,形成正、反记忆网络双向训练,从负荷数据的不同时序提取数据特征。多层堆叠形态的LSTM 神经网络各层之间的关联如下所示:

图2 多层双向LSTM神经网络结构

2.3 基于数据聚类的负荷预测流程
通过对历史负荷数据进行基于气象因素的聚类分析,构建多层双向LSTM 神经网络的短期负荷预测模型,具体流程如图3所示,负荷预测过程分两个阶段,分别为负荷训练样本数据的聚类分析和负荷预测。

图3 负荷预测流程
第一阶段:负荷训练数据的多核均值聚类。构建基于高斯核和线性核组合的多核模糊C 均值聚类方法,实现多特征气象因素样本数据集的低维非线性空间映射至高维线性空间,通过指标评价构建负荷样本训练数据。
第二阶段:多层双向LSTM 神经网络预测。基于训练数据构建短期负荷预测模型进行负荷预测,在神经网络训练过程中利用预测误差评价指标优化神经网络参数,评价指标主要有平均绝对百分比误差MAPE、平均绝对误差MAE和均方根误差RMSE。

式中:yi为实际测量负荷数据;预测模型输出负荷数据;M为负荷样本数量。
3 仿真验证
为了验证本文方法的合理性和准确性,本文采用配电网变电站实际运行数据和相关气象数据进行仿真验证。负荷训练样本数据的采样精度为5 min和15 min两个时间尺度,负荷训练数据为一个月的数据量,预测未来一天和星期进行分析。在进行气象因素聚类时,聚类核函数参数σ=0.005、隶属度函数模糊指数m=1.08、收敛阈值ε=0.000 1,聚类迭代次数为300 次、聚类簇为c=3。本文采用python 开发LSTM 深度神经网络,电脑配置为I9-9900k-3.6GHz,16G内存。
3.1 气象因素聚类分析
利用多核模糊C 均值聚类模型分析负荷训练数据中的气象影响因素,利用多核模糊C 均值聚类模型对原始数据集样本进行聚类处理。样本数据中影响因素为平均温度等8种气象数据。通过多核模糊C 均值算法聚类后的样本数据分布结果如图4所示,从图4中可以看出,聚类模型将多维气象因素聚类为两类,两类子簇之间有边界清晰,其聚类结果的误差不超过4%。基于上述8中气象数据的负荷相关性分析如表1所示,聚类结果的各项指标如表2 所示,多核模糊C 均值聚类较FCM(模糊C 均值)、KFCM(单核模糊C 均值)和DBSCAN(密度聚类算法)在NMI(标准化互信息)、ACC(准确度)、RI(兰德系数)和ARI(调整兰德系数)等4 个指标都具有更加合理的聚类效果。
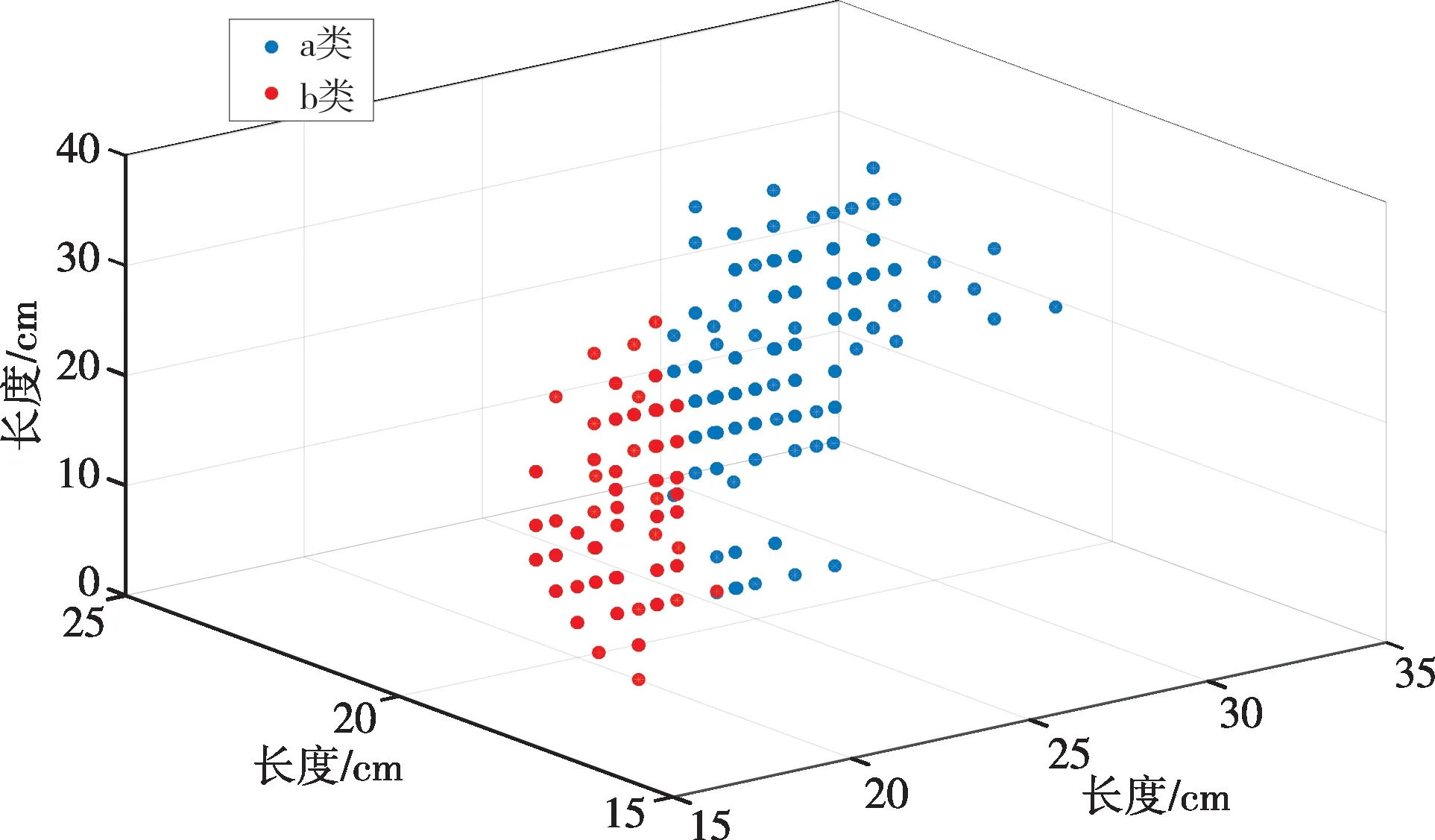
图4 数据集1三维分布
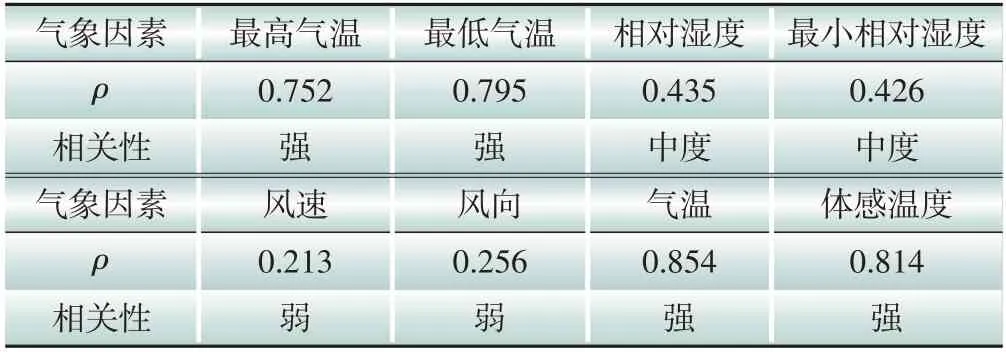
表1 不同影响因素的斯皮尔曼相关系数
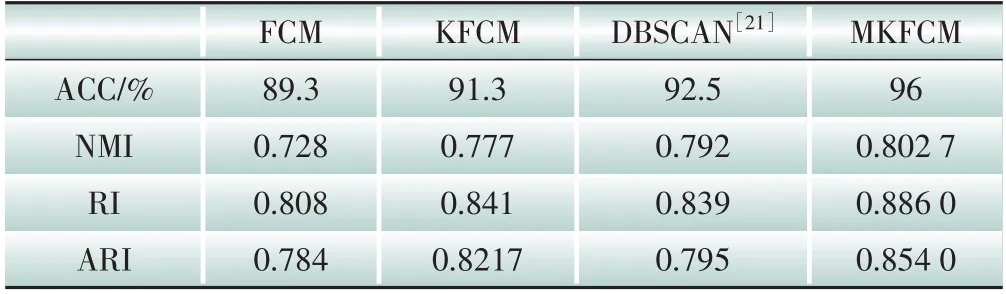
表2 不同聚类算法比较
3.2 神经网络层数选择
利用多层堆叠神经网络进行负荷预测,此时不同层数的神经网络在不同程度上提取数据特征,神经网络层数和最终预测精度存在一定的关系。表3给出了神经网络模型层数与预测误差之间的关系,本文神经网络的层数为3层。图5给出了不同预测方法的结果对比,由图5 可知多层双向LSTM 模型的预测结果相较于传统LSTM 模型、双向LSTM神经网络以及BP网络,预测结果更加接近负荷真实值。

表3 多层堆叠双向LSTM层数与预测误差

图5 不同神经网络预测的对比
3.3 基于聚类分析的负荷预测
通过聚类分析将影响因素根据其对负荷的影响进行聚类划分,进一步的对比不同算法的负荷预测结果。经过聚类分析后,将训练数据的影响因素分为a和b两类,分别进行基于MBLSTM(多层双向长短期记忆)神经网络预测,结果如图6 所示,图7 给出了不同LSTM 神经网络的预测结果对比,预测误差的定量分析如表4所示。由表4可知在考虑气象因素并对其进行聚类分析后,误差从1.44%降低至0.25%。通过气象因素聚类,能够有效甄别影响因素相似的负荷数据,由此提高训练数据的相似性,但是并没有增加计算负担,考虑气象因素比不考虑气象因素的计算时间增加了0.96 s。
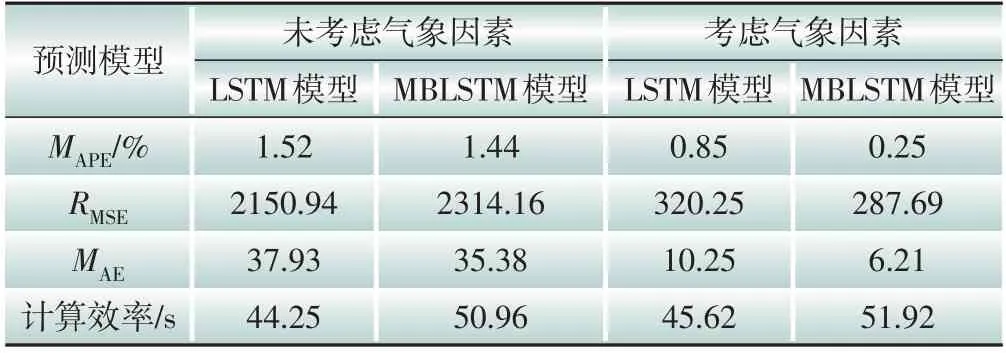
表4 负荷预测误差对比

图6 a、b类数据预测结果

图7 考虑气象因素聚类前后负荷预测
为进一步验证本文方法的合理性,利用冬季负荷数据进行仿真分析,此时负荷预测的结果如图8所示。利用聚类划分处理训练样本数据并以此进行预测大大降低了气象因素对负荷训练、预测过程的影响。从表5可以看出,未考虑气象因素的短期负荷预测模型的MAPE 误差值在4.15%,由于冬季负荷的敏感性较低,整体上冬季负荷预测的误差较夏季大,考虑气象因素分类整体预测误差为0.65%。

图8 考虑聚类气象因素负荷预测结果

表5 负荷预测误差对比
4 结语
本文提出了基于多层模糊C 均值聚类和MBLSTM神经网络的短期负荷预测方法。通过多层模糊C 均值聚类将负荷气象影响因素进行低维空间映射,实现影响因素的精确分类和聚合,明确负荷气象因素的耦合关系;进一步的,提出多层堆叠形式的双向LSTM 神经网络,通过构建双向计算机制和多层堆叠形式,提高负荷数据间的前后关联,挖掘负荷序列数据关联信息,从而提高负荷预测精度。仿真结果表明,本文所提方法能够提高负荷影响因素的区分度,有效提高负荷预测精度。
