Several rough set models in quotient space

Huanmin Zhao|Liwen Ma

School of Science,Beijing University of Posts and Telecommunications,Beijing,China

Abstract In order to deal with coarse-grained and multi-grained calculation problems, as well as granularity transformation problems in information system, quotient space theory is introduced in rough set theory.The main idea of this research is to try to maintain the important properties of the original space into the quotient space.Aimed to preserve the micro properties and the macro properties,two pairs of approximation operators on the quotient space are defined.When it comes to the composite of quotient spaces,the idea of these operators shows greater advantages.Examples are cited to illustrate possible applications of these operators, and their matrix representations are also given to make the calculations easy.Finally,all approximation operators on the quotient space involved so far are compared and their relationships are shown through a diagram.

1|INTRODUCTION

Since rough set theory[1]was introduced by Z.Pawlak to deal with inconsistent and incomplete information in 1982, its effectiveness has been widely proved in many fields, such as computer science, engineering calculation, and information technology.[2-6].The classical rough set theory is based on an equivalence relation that constitutes a partition of the universe,and the partition is regarded as a kind of knowledge being composed of definable sets, then the uncertain sets are approximated by the definable sets in this theory.However,in many practical problems, forming an equivalence relation is too strict to apply the theory.In this situation,researchers have generalized classical rough set theory from multiple angles[7-22].Covering rough set theory which replaces partition with covering is one of generalized rough set theories[7, 8, 12, 13,20, 21, 23] and based on a covering, the notion of neighbourhood of each element in the universe was given.Then many types of approximation operators[7,8,24-27]based on the neighbourhoods were defined and their properties were investigated.To simplify the calculation, matrix methods have also been applied as a useful tool to study rough set theory[9, 28, 29].

Quotient space theory is used to provide a suitable granularity space [30, 31] to describe and solve problems, as well as to establish the connection between different granularity spaces to simplify the problems [30, 32-34].In reality,humans are always confronted with large amounts of complex information with limited cognitive abilities.In this case,complex information can be thought as coarse-grained objects which are composed of fine-grained objects, then the knowledge of fine-grained objects is taken to describe coarsegrained objects.Under an equivalence relation, the quotient space of a covering approximation space can describe the information granulation well, and it is wished that the excellent rough properties in original space can be well preserved in the quotient space.At present, quotient space is seldom introduced into rough set theory.In previous studies,Wang et al.[35] classified elements with the same neighbourhood into the same equivalent class by defining a consistent function, and then defined the images of the covering blocks of the original space as the covering of the image space.This article analysed the rough sets in a very particular image space which is essentially a special quotient space.It is a good innovation, however, the general quotient space under this type of covering cannot preserve theproperties of the original space, either at the micro level or at the macro level.

Here, the study of rough sets in quotient approximation spaces of a covering approximation space is carried out, and it is known that it must be closely related to the original space to make sense.Therefore, the main idea of this research is to try to maintain the important properties of the original space.On the basis of the preliminary study in article [36], a new covering of a given quotient space is defined so that descriptors' characteristics in original space are preserved completely in quotient space, and the quotient space with this type of covering is called as quotient covering approximation space.Then, two pairs of approximation operators on the quotient space are defined and it is found that the approximation effect of the second pair of operators is better than that of the first pair.Also, by combining these two pairs of operators, a reasonable solution is proposed to a coarse-grained problem.Next, the composite of quotient spaces to solve a coarser-grained problem is discussed.In addition, depending on the results of Ma's article [28], the matrix formulas of those two pairs of approximation operators on the quotient approximation space are defined to make the calculation easier.All approximation operators involved on the quotient space were also compared and a diagram to show their relationships is given.

The rest of this article is organized as follows.In Section 2,some basic concepts and properties are recalled.In Section 3,a quotient covering approximation space is defined and then the neighbourhood in this space is given.In Section 4,two pairs of approximation operators on the quotient spaceare given, as well as research on their basic properties and applications are carried out.The matrix representations of those two pairs of approximation operators are given in Section 5 and the composite of quotient spaces is introduced in Section 6.In Section 7, all the approximation operators involved on quotient space are compared and the conclusion of this article is made in Section 8.

2|PRELIMINARIES

In this section,some fundamental knowledge that will be used in this article are recollected.The notation ‘A⊂B’ in this article represents that‘the setAis a strict subset of the setB'or‘the setAis equal to the setB’.

Definition 1[16, 17].LetUbe a finite set and C be a family of subsets ofU.If none of the elements in C is empty andU=∪C∈CC, then C is called a covering ofU, and the ordered pair （U，C） is called a covering approximation space.

Definition 2[17].Let （U，C） be a covering approximation space.For each elementx∈U, a neighbourhood of x is defined asN（x）=∩｛C∈C:x∈C｝.

NeighbourhoodN(x) is the minimum descriptor while describing characteristics ofx.Depending onN(x), a pair of approximation operators is defined and has been widely used in rough set theory.

Definition 3[11].Let （U，C） be a covering approximation space andXbe a subset ofU.The lower approximationP-（X） and the upper approximationP+（X） ofXare defined as

From definitions of the lower approximation operator and upper approximation operator, we can easily get the following properties:

Next, some basic concepts related to the quotient set are recalled.

Definition 4[37].SupposeRis an equivalence relation onU,for each elementx∈U,the subset which can be described as｛y∈U:xRy｝ is called the equivalent class ofx, and the family of equivalent classes is defined as a quotient setU/Rdetermined byR.

Proposition 1[37].Given an equivalence relation RonU,and setV=U/R,then for eachY⊂V,we haveY=R(R-1 （Y ）).

Proposition 2[37].Given an equivalence relation RonU,and setV=U/R,then the inverse ofRsatisfies the formula:

for anyA,B⊂V=U/R.

3|NEIGHBOURHOOD IN QUOTIENT COVERING APPROXIMATION SPACE

In this section, a quotient covering approximation space is constructed with the type of covering of a given quotient space in [36] for the sake of preserving characteristic of neighbourhoods in original space.Then the neighbourhood ofyin quotient covering approximation space is given.

Definition 5Given a covering C=｛C1，C2，…，Cl｝ofUand an equivalence relationRonU, setthen CRis a covering ofV=U/R.The ordered pair（V，CR）is called a quotient covering approximation space of（U，C）.

Example 1

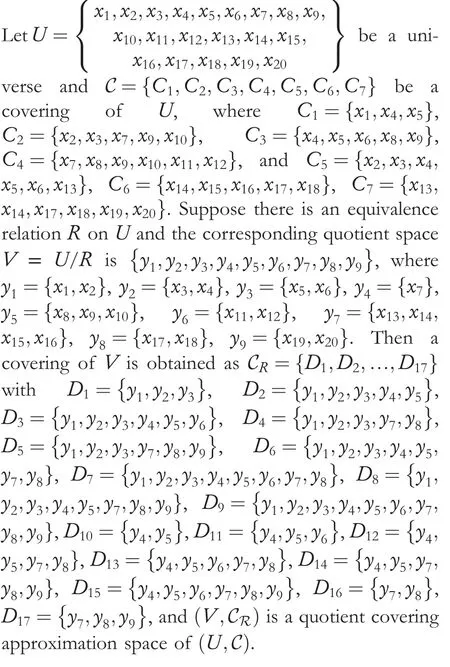
According to the covering of quotient space, the neighbourhood ofyin quotient space can be further defined.

Definition 6Let （V，CR） be a quotient covering approximation space of （U，C）.For each elementy∈V, the neighbourhood ofyis defined asn（y）=∩｛D∈CR:y∈D｝.

Here a practical example is given to introduce the meaning of each formula in the original space and in the corresponding quotient space.

Example 2Leading industries of a city can be used to judge whether a city is polluted or not.If Ministry of Environmental Protection wants to govern polluted provinces under limited conditions, such as, it only knows the leading industries of each city and has limited material conditions, then the first step is to get the details of the leading industries of the provinces.SupposeUis a collection of some cities in the country and C is the collection of leading industries of all cities inU.LetVbe the collection of provinces to which all cities inUbelong.Then it is assumed that （U，C） and（V，CR） are the same as that in Example 1.

Ifx∈Ci∩Cj, then cityxhas both leading industriesCiandCj.SoN（x）=∩｛C∈C:x∈C｝ reflects the leading industries ofx,on the other hand,it can also represent the cities which own the leading industries ofx.In definition, CRis a collection of the ranges of leading industries of each province inV.As given in Example 1,the leading industries ofy1are in the range of leading industries｛C1，C2，C3，C5｝.Ifyi,yj∈Dm, whichDmis represented byCiwhereCi∈C, thenyi's leading industries andyj's leading industries are within the rangeDmbut not necessarily identical.By this means,n(y)reflects the smallest range of leading industries ofyinV.

Certainly, it also represents the smallest set of provinces whose leading industries are also within the range of leading industries ofy.

Now the connection between neighbourhoodsn(y) andN（x） under the equivalence relationRis taken into consideration.

Proposition 3[36] Let（U，C）be a covering approximation space and（V，CR）be the quotient covering approximation space of（U，C）.For each element y∈V, we haven（y）=Proof.According to the proposition in[36], which

ActRon both sides of the formula, then

This proposition obviously indicates that ifx∈R-1（y）⊂R-1（n（y））, thenR（N（x））⊂n（y）.This means that properties of the minimum descriptorN（x）in the original space are completely preserved byn（y） in the quotient space,and this is why such type of covering is defined on the quotientspace.Next, the data from Example 1 is used for testing this conclusion and give an actual explanation about the advantages of this proposition according to Example 2.Here, only considery1∈Vas a representative to show this point.

In Example 2, these results mean that when cityx4owns the leading industries of the cityx1, there will be the leading industries of provincey2containing the cityx4are also within the smallest range of leading industries of the provincey1containing the cityx1,so doesx5.Also,when cityx3owns the leading industries of cityx2, then the leading industries of provincey2containing the cityx3are also within the smallest range of leading industries of the provincey1containing the cityx2and so on.Hence,from the perspective of the range of the leading industries of provinces inV, Ministry of Environmental Protection can adopt the same governance asy1to governy2andy3.

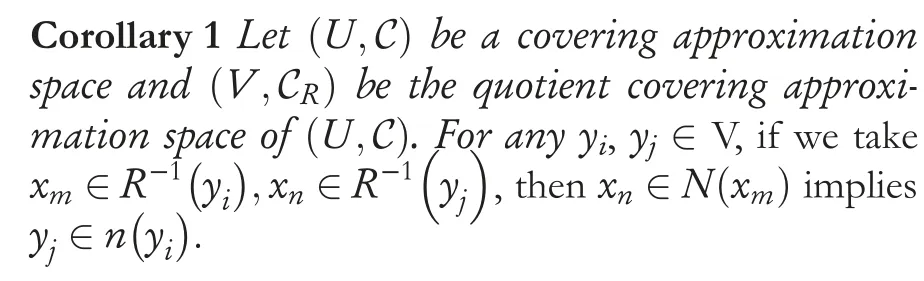
Proof.It directly follows from Proposition 3 that

4|TWO PAIRS OF APPROXIMATION OPERATORS ON QUOTIENT SPACE

Based onn(y),now the first pair of approximation operators is given on（V，CR）.This pair of operators can be understood as preserving the properties of the original space from the micro perspective.

Definition 7Let （U，C） be a covering approximation space and （V，CR） be the quotient covering approximation space of（U，C）.For eachY⊂V,we define the lower approximationp-(Y) and the upper approximationp+(Y) ofYas

In order to make the approximation operators on the quotient space retain the properties of approximation operators on the original space from the macro perspective, the approximation operators on the original space are used directly for defining the approximation operators on the quotient space.So the second pair of lower approximationp-*(Y) and upper approximationp+*(Y) ofYare given as follows.

Definition 8LetVbe a quotient space of a covering approximation space （U，C）.For eachY⊂V, the lower approximation ofYis defined as:

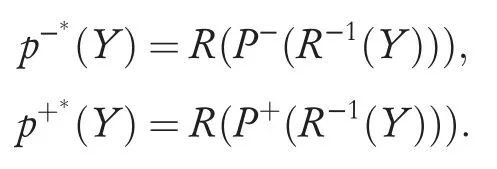
It is worth mentioning that this pair of operators requires only a covering ofU, not a covering ofV.

It can be seen that the first pair of approximation operators on quotient space has the same form as the pair of approximation operators in Definition 3.Also,relying on the excellent properties ofn(y), it can be proved thatp-has propertiesP（1）-P（6）, andp+has propertiesQ（1）-Q（6）.Now the properties of the second pair of approximation operators

Proposition 4Let Vbe a quotient space of a covering approximation space （U，C）.For eachY⊂V, we have

Proof.The first equation is to be proved.

For each element.y＇∈p-＊（Y）

Then the second equation is to be proved.

For each elementy＇∈p+＊（Y）

Notice that the equivalence of Equations (2) and (3) is determined by Proposition 2, and it must be noted thatRis a special relation—the equivalence relation.

Exactly as discussed above, the second pair of approximation operators can be transformed into the expressions determined by the image of neighbourhoods of elements in original space.Therefore,it will be easier to study the following propositions.

Proposition 5Let Vbe a quotient space of a covering approximation space （U，C）.For eachY⊂V, the lower approximation operatorp-＊satisfies propertiesP（1）-P（4）.

Proposition 6Let Vbe a quotient space of a covering approximation space （U，C）.For eachY⊂V, the upper approximation operatorp+*satisfies propertiesQ（1）-Q（5）.

Proof.ConditionsQ（1）-Q（3） are obvious, so proofs ofQ（4） andQ（5） are given.

As desired.

Next the proof ofQ（5） is given.

For anyY1,Y2⊂V, sinceP+satisfiesQ（5）, we can get

Proposition 3 presents a definite formula betweenn（y）andR（N（x））wherex∈R-1（n（y） ）.It is very important,and it can be taken to build the relationship between the two pairs of approximation operators.

Proposition 7Let V be the quotient space of a covering approximation space（U，C）.For each Y⊂V,the relationships among the lower and upper approximations ofYunder the two pairs of approximation operatorsare:

This example also shows that every containment relationship in the formula of Proposition 7 is generally not an equality.

Proposition 7 tells us the fact that the second pair of operatorshas better approximation effect than that of the first pair（p-，p+）.By taking advantage of that, these two pairs of operators can be combined to solve the practical problem in Example 1.

Example 7In Example 2, it is assumed thatC1,C5,C7are the leading industries that cause cities to get polluted, which indicates that if cityx∈Ci,i= 1, 5,7, then it is a polluted city.However, the province to which the cityxbelongs is not necessarily polluted,for whether a province is polluted is determined by its leading industries.The information Tables 1 and 2 are provided to show the pollution of cities inUand the pollution of provinces inVaccording to the data in Example 1, and the information Table 2 is inconsistent.

Under limited material conditions, if Ministry of Environmental Protection wants to give priority to govern polluted provinces, then the models of the two pairs of approximation operators can be taken into account.

As for the polluted provincesy1,y7in Table 2 and the results of Example 6, the provincey7can be governed firstly,which is selected by the second pair of operators from the polluted provincesy1,y7.Provincey1can be governed secondly,provincesy2,y8,y9can be governed thirdly,provincey3can be governed fourthly,and provincesy4,y5,y6need not be governed.

5|MATRIX REPRESENTATIONS OF THE TWO PAIRS OF APPROXIMATION OPERATORS

In this section,matrix representations of the two new pairs of approximation operators introduced in Section 4 are given.Through matrix calculation, the abstract calculations of definitions simple and straightforward can be made, especially when the data is very big.

T A B L E 1 A table of the pollution of cities in U

T A B L E 2 An inconsistent table of the pollution of provinces in V

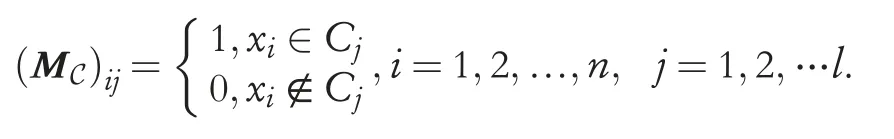
The matrix representation depends on the orders of the elements inU.In fact, the main results of the calculationformulas in this section are not affected by these orders.So any given order will be determined.

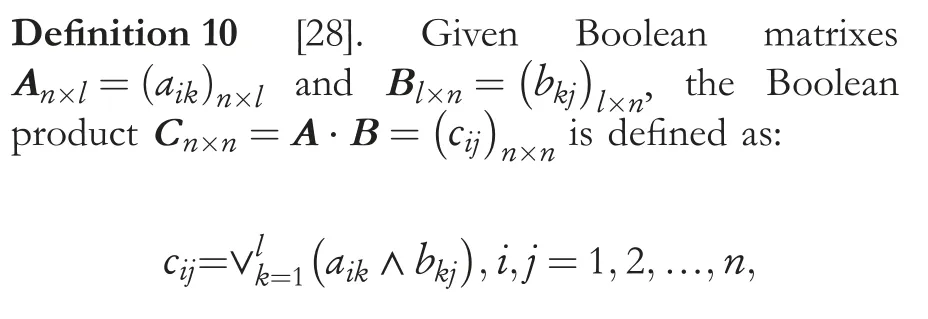
where ∨and ∧mean the max and the min operations,apparently,the Boolean productCn×nis still a Boolean matrix.

In Ma's article [28], it has been found that the way to calculate the upper and lower approximations of a rough set by defining the product of Boolean matrices.

Then it can just take the relational matrixNRofRinto account to study the matrix representations of

Proof.It follows from Proposition 8 thatχY=NRT·χX.So, according to the Proposition 9 in article [28], the result is obtained.□

Next,an algorithm for calculating the neighbourhoodn（y）of each elementyin the quotient spaceVof （U，C） is given.

Then the matrix representations of（p-，p+） can be surely obtained on the basis of the Boolean matrix…，m｝ is the family of neighbourhoods of elements in

Proposition 11Let（V，CR）be a quotient covering approximation space of a covering approximation space（U，C）, then for each Y⊂V, we have

Proof.DenoteMBT·χY=［b1，b2，b3，…，bm］T, thenbi= 1

Next, a concrete example to show how to use Boolean matrix for computing the upper and lower approximations of subsets in quotient covering approximation space under the two pairs of operators is given.

and

6|ROUGH SETS IN THE COMPOSITE OF QUOTIENT SPACES

In this section, the rough sets in the composite of quotient spaces,that is,the quotient space of a quotient space is studied.For the reason that we are always confronted with more complex objects which we have a little knowledge to describe them.

IfVis a quotient space ofUandWis a quotient space ofV, the approximation operators onWis defined in the same way as the operators in Definition 7 and Definition 8.

Definition 13Let （V，CR1） be a quotient covering approximation space of a covering approximation space（U，C）.Given an equivalence relationR2onV, a quotient spaceW=V/R2ofVis obtained,it is called as W the composite of quotient spaces, that is, the quotient space of the quotient space of the covering approximation space （U，C）.The covering ofWis defined asthen theneighbourhood of each elementzinWis defined as:n＇（z）=∩｛H∈CR2:z∈H｝,and for eachB⊂W,three pairs of approximation operators onWcan be defined as:

Proposition 13Let（W，CR2）be a quotient covering approximation space of a covering approximation space（V，CR1）which is also a quotient spaces of a covering approximation space（U，C）.For each element z∈W, we have

The next proposition is directly followed from Propositions 7 and 13.

Proposition 14Let V be the quotient space of a covering approximation space（U，C）and W be the quotient space of V.For each B⊂W, the approximations ofBunder the three pairs of operators will have the following relationships:

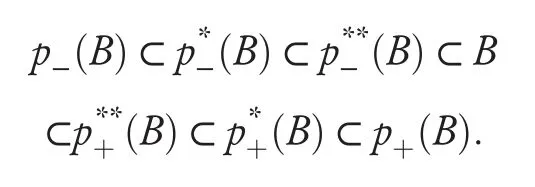
An example is given to show that every inclusion relation in this proposition is generally not equal.

Next, an example is given to show the simple applications of these three pairs of operators.

Example 10In Example 2, supposeWis a collection of China regions such as North China, and the provinces belonging to the same China region are treated as one class, namely,Wis a quotient space ofV.Using the similar analytical methods in Examples 2 and 7, a reasonable strategy can be further provided for governing the pollution of China regions.

Information Table 3 is also inconsistent, which shows the pollution of the China regions inWbased on the data in Examples 7 and 9.

Under limited material conditions, if Ministry of Environmental Protection wants to give priority to govern the polluted China regions, then combining the information Table 3 with the results of Example 9,Ministry of Environmental Protection can governz5firstly,z1secondly,z2thirdly,z3fourthly andz4need not be governed.

Also,the approximations ofB2in Example 9 show the fact that the third pair of operatorsis the most effective in selecting the unpolluted Chinese regions, which will save a lot of manpower and physical resource besides offer a newsolution to the pollution problem.Here it should be also pointed out that when an inconsistent information table is processed, the result of the first pair of operatorsis always the basis of judgment.

7|RELATIONSHIPS AMONG ALL OPERATORS INVOLVED ON THE QUOTIENT SPACE

The purpose of giving these new operators in this article is to maintain the micro and macro properties of the original space effectively.In fact, given a quotient spaceU/Rof a covering approximation space （U，C）, it is quite natural to think about the covering ofVwhich is Δ=｛R（C）:C∈C ｝.Wang [35]followed the same approach and took this covering to deal with a special quotient space.

Based on this covering, then the definition of neighbourhood in the quotient space is given.

Definition 14Given a covering C=｛C1，C2，…，Cl｝ofUand an equivalence relationRonU, then Δ=｛R（C）:C∈C ｝ is obviously a covering of quotient spaceV=U/R.For each elementy∈V, the neighbourhood ofyis defined asn＊（y）=∩｛M∈Δ:y∈M｝, which is a natural definition in the covering approximation space (V, Δ).

Proposition 3 indicates thatx∈R-1（y） impliesR（N（x） ）⊂n（y）.However,the neighbourhoodn*(y)obtained by the covering Δ of the quotient spaceVcannot get this conclusion.Here we also takey1∈Vin Example 1 to illustrate this point.

In Example 2, the definition of covering Δ of quotient space means that it just corresponds the leading industries of cities to the leading industries of the province directly, that is,the leading industries of each city are the leading industries of the provinces to which these cities belong.This definition of covering Δ is not comprehensive enough to solve problemsand deviates from the fact,so,the covering CRin Definition 5 is more aligned with the actual situation.

T A B L E 3 An inconsistent table of the pollution of China regions in W

Relying onn＊（y）,another pair of approximation operators are obtained.

Definition 15Let (V, Δ) be a quotient covering approximation space of a covering approximation space （U，C）.For eachY⊂V, the lower and upper approximations ofYare defined asrelationships between the three operatorsand（p-，p+）.

The above two examples state that these three pairs of approximation operators on quotient space have no explic it inclusion relationships.Since the pair of operatorsis not a dual pair, here their dual operators are taken into account.

Definition 16LetVbe a quotient space of a covering approximation space（U，C）.For eachY⊂V,the dual approximation operator E+of p-*is denoted by

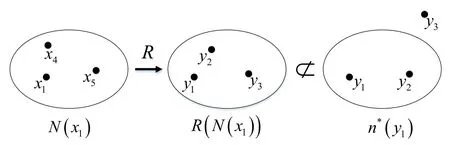
F I G U R E 3 The figure of R （N （x 1））⊄n＊ (y1)

F I G U R E 4 The figure of the relationships of all operators on the quotient space

The dual approximation operator F-ofp+*is denoted by

The following properties of operatorE+and operatorFcan be obtained.

Proposition 15Let Vbe a quotient space of a covering approximation space （U，C）.For eachY⊂V,

Proof.Proofs of these two equations are similar,here only the first equation is proved.

Proof.From Propositions 4 and 15,it is easy to obtain thatOwi ng to the duality ofp+andF-as well as the duality ofp+ and

For convenience,a picture is drawn as follows to express the relationships among them,where the lower element is a subset of the upper element when they are linked by one line Figure 4.

The relationships among the various existing models are discussed so that it could be applied better for different practical needs.

8|CONCLUSION

For a given quotient space of a covering approximation space, a new view to define its covering is provided which had many favourable properties.Then two pairs of approximation operators on the quotient space were given, which could be regarded as an attempt to retain micro and macro properties from the original space.It is proved that the second pair of operators not only had better approximation effect than that of the first pair, but also had advantages to investigate the composite of quotient spaces to deal with coarser-grained problems.To make the calculation clearer and simpler, the matrix representations of the two pairs of approximation operators were given.In the end, all the approximation operators on the quotient space involved so far were compared and the definition 5 of quotient covering approximation space that has much practical value is explained.

ACKNOWLEDGEMENTS

This research is supported by the National Natural Science Foundation of China under Grant 61672107 and funded by the China Scholarship Council (201606475016).

In the process of writing this article, the authors express heartfelt gratitude to a fellow scholar Hui Lu for the great help that was provided.

Algorithm 1 Calculate the neighbourhood n(y) of each elementyin the quotient spaceV

?

4.Pawlak, Z., Skowron, A.: Rough sets and Boolean reasoning, Inf.Sci.177(1), 41-73 (2007).https://doi.org/10.1016/j.ins.2006.06.007

5.Dai, J.H., Xu, Q.: Approximations and uncertainty measures in incomplete information systems, Inf.Sci.198, 62-80 (2012).https://doi.org/10.1016/j.ins.2012.02.032

6.Wang, X.Z., et al.: Learning fuzzy rules from fuzzy samples based on rough set technique, Inf.Sci.177(20), 4493-4514 (2007).https://doi.org/10.1016/j.ins.2007.04.010

7.D'eer, L., et al.: Neighborhood operators for covering-based rough sets,Inf.Sci.336, 21-44 (2016)

8.Ma,L.W.:On some types of neighbourhood-related covering rough sets,Int.J.Approx.Reason.53(6),901-911(2012).https://doi.org/10.1016/j.ijar.2012.03.004

9.Ma,L.W.:Two fuzzy covering rough set models and their generalizations over fuzzy lattices,Fuzzy Set Syst.294,1-17(2016).https://doi.org/10.1016/j.fss.2015.05.002

10.Zhu, W.: Relationship between generalized rough sets based on binary relation and covering, Inf.Sci.179(3), 210-225 (2009).https://doi.org/10.1016/j.ins.2008.09.015

11.Yao, Y.Y.: Relational interpretations of neighbourhood operators and rough set approximation operators, Inf.Sci.111(1-4), 239-259 (1998).https://doi.org/10.1016/s0020-0255(98)10006-3

12.Zhu,W.,Wang,F.Y.:On three types of covering-based rough sets,IEEE Trans.Knowl.Data Eng.19(8), 1131-1144 (2007).https://doi.org/10.1109/tkde.2007.1044

13.Liu, G.L., Sai, Y.: A comparison of two types of rough sets induced by coverings, Int.J.Approx.Reason.50(3), 521-528 (2009).https://doi.org/10.1016/j.ijar.2008.11.001

14.Zhang, Y.L., Luo, M.K.: Relationships between covering-based rough sets and relation-based rough sets, Inf.Sci.225, 55-71 (2013).https://doi.org/10.1016/j.ins.2012.10.018

15.Mareay,R.:Generalized rough sets based on neighbourhood systems and topological spaces, J.Egypt.Math.Soc.24(4), 603-608 (2016).https://doi.org/10.1016/j.joems.2016.02.002

16.Bonikowski, Z., Bryniarski, E., Wybraniec-Skardowska, U.: Extensions and intentions in the rough set theory,Inf.Sci.107(1-4),149-167(1998).https://doi.org/10.1016/s0020-0255(97)10046-9

17.Zhu,W.:Topological approaches to covering rough sets,Inf.Sci.177(6),1499-1508 (2007).https://doi.org/10.1016/j.ins.2006.06.009

18.Yao,Y.Y.:Two views of the theory of rough sets in finite universes,Int.J.Approx.Reason.15(4),291-317(1996).https://doi.org/10.1016/s0888-613x(96)00071-0

19.Mi, J.S., Zhang, W.X.: An axiomatic characterization of a fuzzy generalization of rough sets, Inf.Sci.160(1-4), 235-249 (2004)

20.Wang, X., Ma, L.W.: Study on covering rough sets with topological methods,CAAI Trans.Intell.Technol.4(3),129-134(2019).https://doi.org/10.1049/trit.2019.0008

21.Ma, L.W.: Couple fuzzy covering rough set models and their generalizations to CCD lattices, Int.J.Approx.Reason.126, 48-69 (2020).https://doi.org/10.1016/j.ijar.2020.08.003

22.Zhang,X.H.,et al.:Neighbourhood systems based attribute reduction in formal decision contexts, CAAI Trans.Intell.Technol.4(4), 245-254(2019).https://doi.org/10.1049/trit.2019.0039

23.Zhu,W.,Wang,F.Y.:Reduction and axiomization of covering generalized rough sets, Inf.Sci.152, 217-230 (2003).https://doi.org/10.1016/s0020-0255(03)00056-2

24.Wu, W.Z., Zhang, W.X.: Neighborhood operator systems and approximations, Inf.Sci.144(1-4), 201-217 (2002).https://doi.org/10.1016/s0020-0255(02)00180-9

25.Yao, Y.Y.: Neighborhood systems and approximate retrieval, Inf.Sci.176(23), 3431-3452 (2006).https://doi.org/10.1016/j.ins.2006.02.002

26.Ma, L.W., Lu, H.: Six-set approximation theorem of neighbourhood related rough sets,Int.J.Approx.Reason.115,180-193(2019).https://doi.org/10.1016/j.ijar.2019.09.011

27.Lin, G.P., Qian, Y.H., Li, J.J.: NMGRS: neighbourhood-based multigranulation rough sets,Int.J.Approx.Reason.53(7),1080—1093(2012).https://doi.org/10.1016/j.ijar.2012.05.004

28.Ma,L.W.:The investigation of covering rough sets by Boolean matrices,Int.J.Approx.Reason.100,69-84(2018).https://doi.org/10.1016/j.ijar.2018.05.008

29.Wang, S.P., et al.:Characteristic matrix of covering and its application to boolean matrix decomposition, Inf.Sci.263, 186-197 (2014).https://doi.org/10.1016/j.ins.2013.10.018

30.Zhao, S., et al.: Relational granulation method based on quotient space theory for maximum flow problem, Inf.Sci.507, 472-484 (2020).https://doi.org/10.1016/j.ins.2018.12.009

31.Lin, T.Y.: Granular computing on binary relations I: data mining and neighbourhood systems, Rough Set.Knowl.Discov.1, 107-121 (1998).http://doi:10.1007/978-0-387-30440-3_327

32.Lin, T.Y., et al.: Intelligent query answering based on neighbourhood systems and data mining techniques, In: Proceedings.International Database Engineering and Applications Symposium, IDEAS'04.IEEE,Coimbra (2004)

33.Zhang, L., Zhang, B.: The Theory of Quotient Space and Its Applications(in Chinese).Peking University Press, Beijing (2007)

34.Liu, B.H., Verbraeck, A.: Multi-resolution modeling based on quotient space and DEVS, Simulat.Model.Pract.Theor.70, 36-51 (2017)

35.Wang, C.Z., et al.: Communication between information systems with covering based rough sets, Inf.Sci.216, 17-33 (2012).https://doi.org/10.1016/j.ins.2012.06.010

36.Zhao, H.M., Ma, L.W.: Study of rough sets in quotient approximation spaces (in Chinese), J.Cap.Normal Univ.41, 7-10 (2020)

37.Munkres, J.: Topology, China Machine Press, Beijing (2004)

38.Geng,S.Y.:Set Theory and Graph Theory(in Chinese),Peking University Press, Beijing (1900)